单源最短路问题
全部代码
全部代码在github acwing 上
正在更新
https://github.com/stolendance/acwing
图论
欢迎大家star与fork
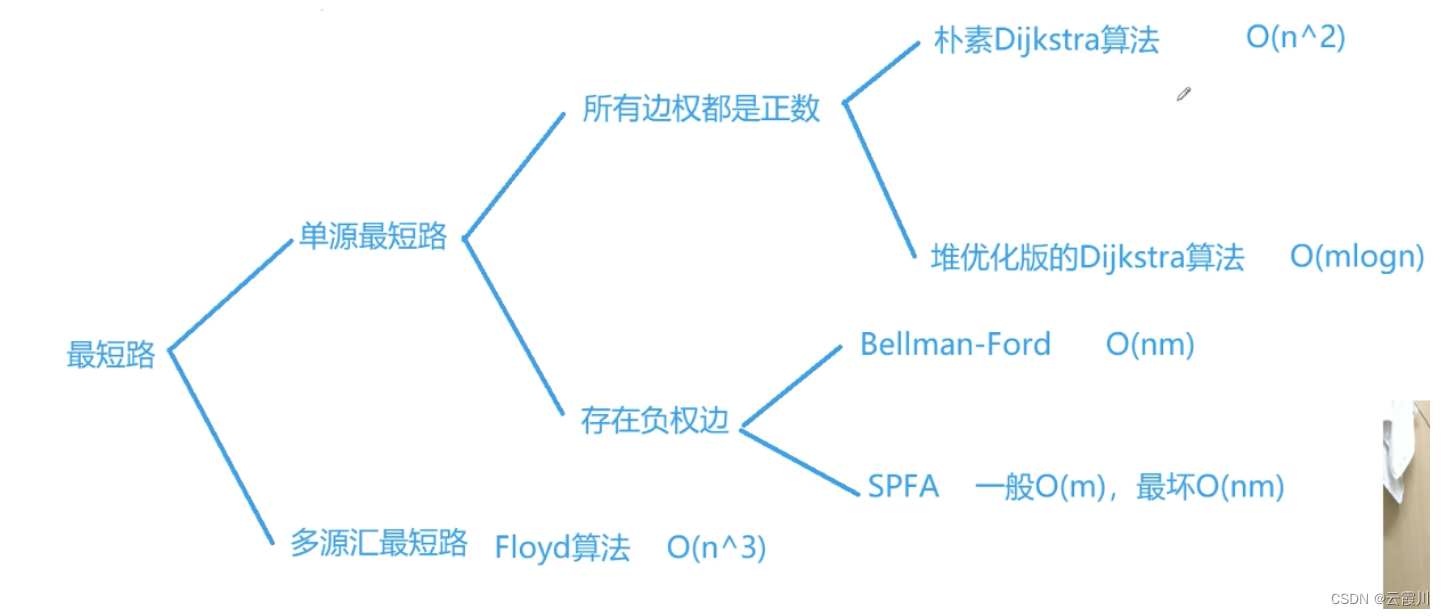
单源最短路问题 先用spfa算法 不行再换其他的
spfa-超级万能 说不定比dijsktra还快
dis[] 代表第k到某一点的最短距离
queue 代表刚被更新的点 它有可能更新其他路径 所以检查它的出边
isin代表该点是否在queue中
队列放入起点 <-k
while(队列不为空)取出队头遍历所有t的出边 t-w>b如果dis[b]>dis[t]+w[t,b],更新,如果b不在队列中,加入b
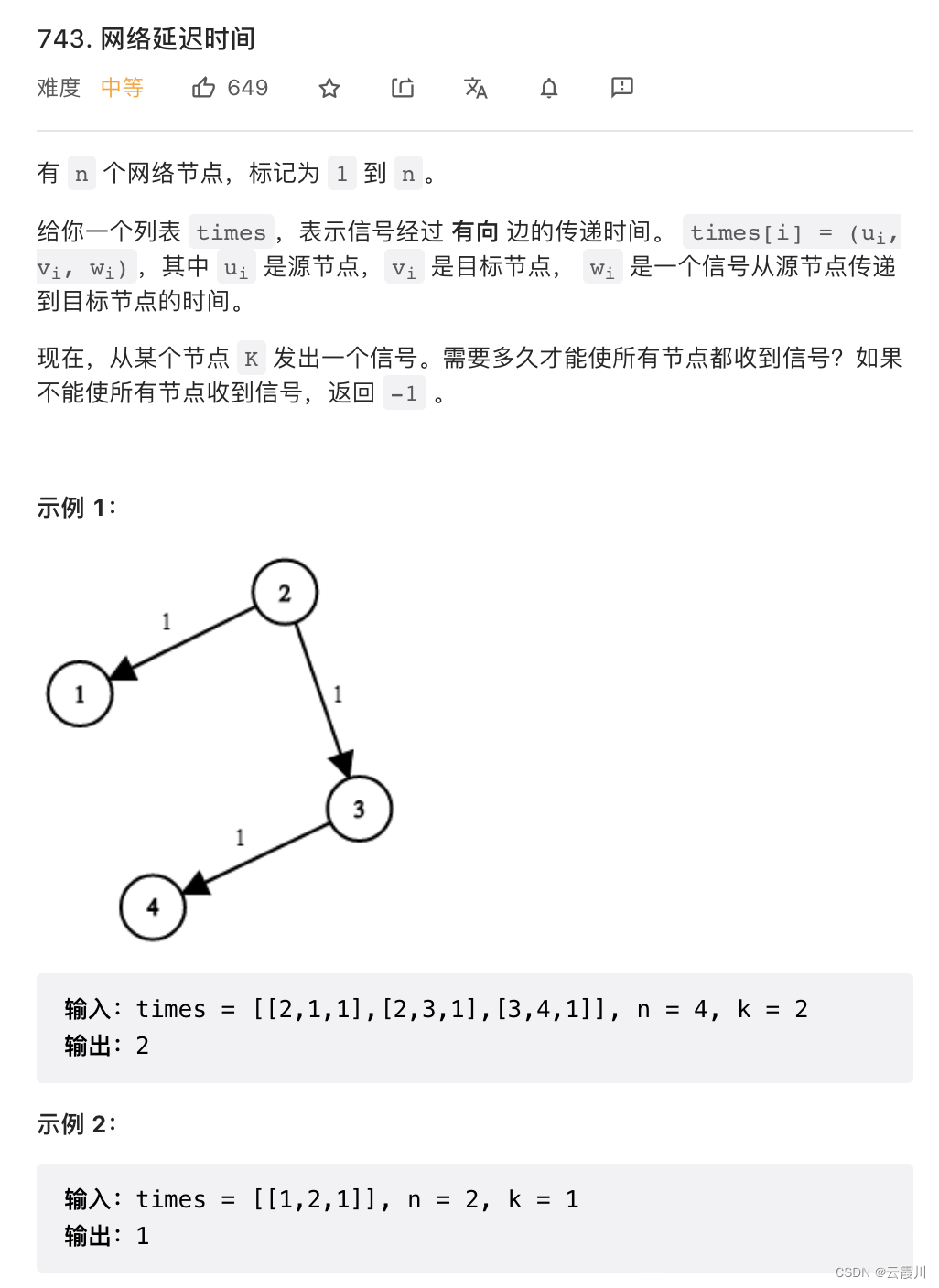
typedef long long ll;
typedef pair<ll,ll> pll;
struct Edge
{int next;int val;Edge(int next_,int val_):next(next_),val(val_){;}
};
class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<vector<Edge> > graph(n+1);for(auto item:times){int a=item[0];int b=item[1];int c=item[2];graph[a].push_back(Edge(b,c));}vector<ll> dis(graph.size(),INT_MAX);vector<int> isin(graph.size(),0);queue<int> ls;ls.push(k);dis[k]=0;isin[k]=1;while(ls.size()){int t=ls.front();ls.pop();isin[t]=0;for(int i=0;i<graph[t].size();i++){// k->t->idint distance=graph[t][i].val;int id=graph[t][i].next;if(dis[t]+distance<dis[id]){dis[id]=dis[t]+distance;if(isin[id]==0){ls.push(id);isin[id]=1;}}}}int rs= *max_element(dis.begin()+1,dis.end());if(rs==INT_MAX) return -1;else return rs;}
};
朴素版dijsktra -单源最短路-所有边权重都是正数 基于 稠密图(邻接矩阵)
s:当前已经确定最短路径距离的点
-
dis[0 ]=0 dis[i]=+OO 只有起点被确定到了
-
for(i 1 …n)
t《- 不在s中的距离最近的点
s〈-t
用t更新其他点的距离(看下)
dij实现的时候是通过 将距离设置成无穷大 来表达 不可达
dij 由于边很多, 稠密图 所以用邻接矩阵存即可
dij 需要找n个点 所以外层是一个for循环x
总结下来:1. 把未加入的最近的加进来2. 标记加入3. 根据加入的点更新距离
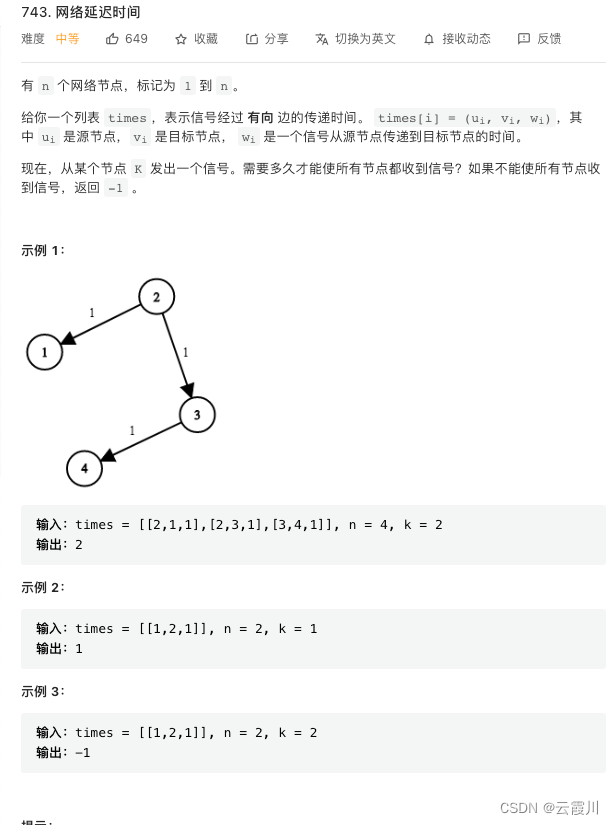
#include<iostream>
#include<vector>
using namespace std;
#define INA INT_MAX
//https://leetcode.cn/problems/network-delay-time/
int networkDelayTime(vector<vector<int> >& times, int N, int k) {// 因为点的坐标是从1开始 , 所以开N+1个// 直接在graph上更新 方便很多// graph要采用long long INT_MAX+某个数 不会变成负数vector<vector<long long> > graph(N+1,vector<long long>(N+1,INT_MAX));for(int i=1;i<=N;i++) graph[i][i]=0;for(auto e:times) graph[e[0]][e[1]]=e[2];vector<int> vis(graph.size(),0);vis[k]=1;// 只要找下除了起点的接下来的点for(int i=1;i<graph.size()-1;i++){int minid=0,minx=INA;// 在没有使用过的检查最短的距离for(int j=1;j<graph.size();j++){if(vis[j]==0&&graph[k][j]<minx){minid=j;minx=graph[k][j];}}vis[minid]=1;// 更新// 根据这个点更新其他所有距离for(int j=1;j<graph.size();j++){graph[k][j]=min(graph[k][j],graph[k][minid]+ graph[minid][j]);}}int ans=0;for(int i=1;i< graph.size();i++){if(graph[k][i]==INT_MAX) return -1;ans=max(ans, (int)graph[k][i]);}return ans;
}
int main()
{vector<vector<int> > times={{2,1,1},{2,3,1},{3,4,1}};int rs=networkDelayTime(times,4,2);cout<<rs<<endl;}
dijstra 稀疏图(邻接表) -我更喜欢的方式!!!
求点k到其他点的距离
与上面不同的情况是, 采用邻接表+最小堆
最小堆 的格式是(点k到该点的距离,该点的id)
dis[] 存储的是点k到达每个点的最短距离
st[] 存储的是否能确定点k到达每个点的距离while(队列不为空)
{队列弹出一个如果该点确定了最短距离,就不管它 if(st[]) continue把弹出的这个点加入最短距离根据这个点进行扩展,遍历这个点指向其他点的边如果比div小,则更新距离加入队列中
}

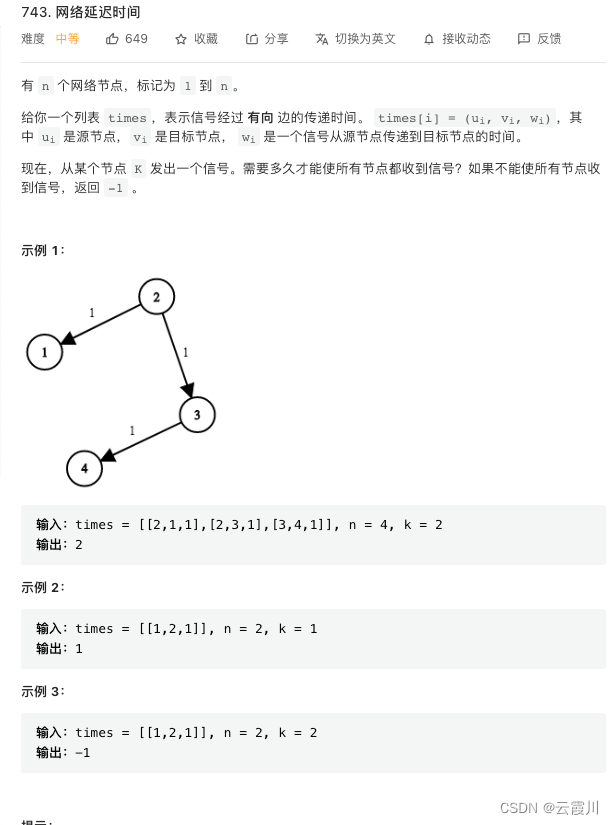
typedef long long ll;
typedef pair<ll,ll> pll;
struct Edge
{int next;int val;Edge(int next_,int val_):next(next_),val(val_){;}
};
class Solution {
public:int networkDelayTime(vector<vector<int>>& times, int n, int k) {vector<vector<Edge> > graph(n+1);for(auto item:times){int a=item[0];int b=item[1];int c=item[2];graph[a].push_back(Edge(b,c));}vector<ll> dis(graph.size(),INT_MAX);vector<int> st(graph.size(),0);priority_queue<pll,vector<pll>,greater<pll> > ls;ls.push(pll(0,k));dis[k]=0;while(ls.size()){auto item=ls.top();ls.pop();ll distance=item.first;int id=item.second;// 保证未加入if(st[id]) continue;// 加入st[id]=1;// 扩展更新for(int i=0;i<graph[id].size();i++){// k->id->id2// distance distance2int id2=graph[id][i].next;int distance2=graph[id][i].val;if(distance+distance2<dis[id2]){dis[id2]=distance+distance2;// 加入队列ls.push(pll(dis[id2],id2));}}}int rs=(int)*max_element(dis.begin()+1,dis.end());if(rs==INT_MAX) return -1;else return rs;}
};
相关文章:

单源最短路问题
全部代码 全部代码在github acwing 上 正在更新 https://github.com/stolendance/acwing 图论 欢迎大家star与fork 单源最短路问题 先用spfa算法 不行再换其他的 spfa-超级万能 说不定比dijsktra还快 dis[] 代表第k到某一点的最短距离 queue 代表刚被更新的点 它有可能更…...

Security方法注解权限控制过程及自定义权限表达式
文章目录 使用内置的权限表达式PreAuthorizePermissionEvaluator 自定义权限表达式SysMethodSecurityExpressionHandler源码流程 SysMethodSecurityExpressionRoot 使用内置的权限表达式 PreAuthorize 这个用来判断超级管理员的话,还得在表达式上加上或 Permissi…...

vue 省市县三级联动
1、 <template><div>所在省<el-select popper-class"eloption" :popper-append-to-body"true"change"getShiList(obj.province)" v-model"obj.province" placeholder"请选择所在省" clearableclear"re…...

ChatGPT实现编程语言转换
编程语言转换 对于程序员来说,往往有一类工作,是需要将一部分业务逻辑实现从服务端转移到客户端,或者从客户端转移到服务端。这类工作,通常需要将一种编程语言的代码转换成另一种编程语言的代码,这就需要承担这项工作…...
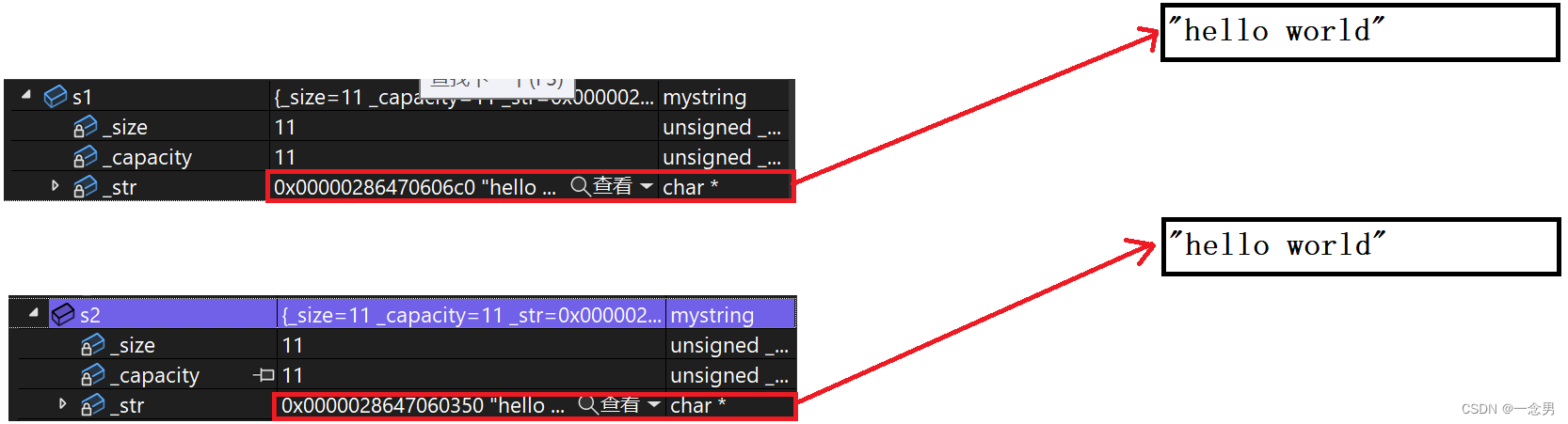
浅拷贝和深拷贝
浅拷贝: 定义:浅拷贝(Shallow Copy)是一种简单的对象复制方式,将一个对象的数据成员直接复制给另一个对象(通常是通过默认的复制构造函数或赋值运算符实现),这些数据成员可以是基本…...
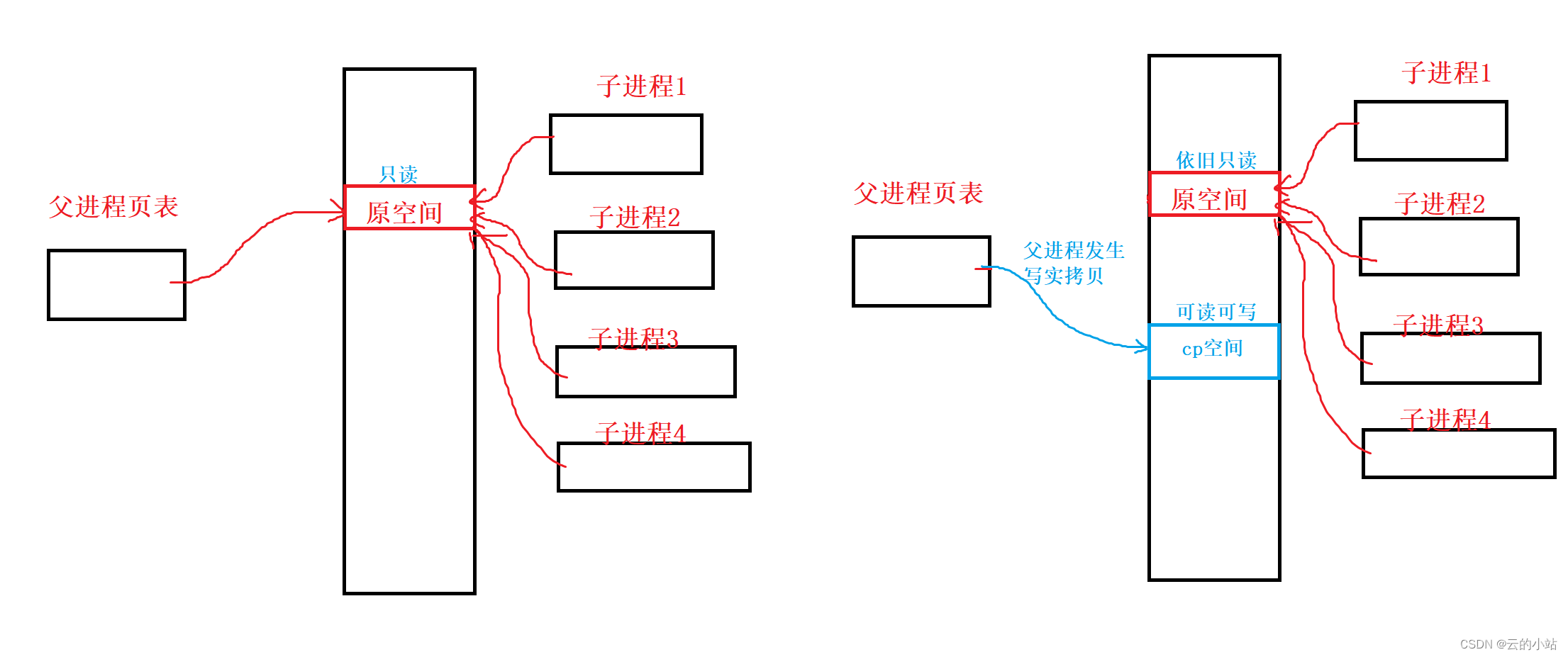
进程地址空间与页表方面知识点(缺页中断及写时拷贝部分原理)
谢谢阅读,如有错误请大佬留言!! 目录 谢谢阅读,如有错误请大佬留言!! 抛出总结 开始介绍 发现问题 进程地址空间(虚拟地址) 页表 物理内存与进程地址空间映射 缺页中断基本…...
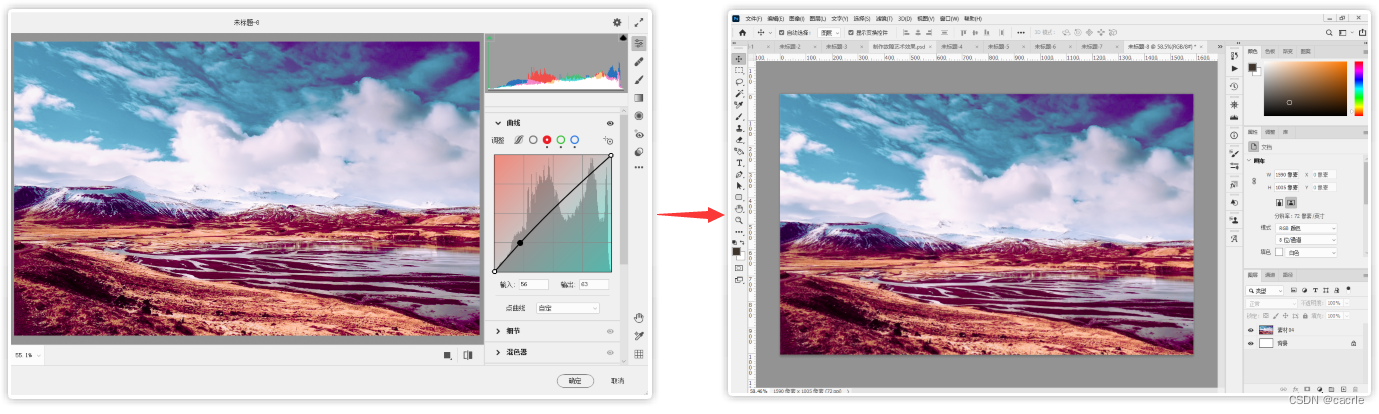
Photoshop如何使用滤镜之实例演示?
文章目录 0.引言1.将普通照片制作成油画效果2.使用液化滤镜修出完美身材3.用镜头光晕滤镜制作唯美的逆光人像4.用Camera Raw滤镜对偏色风景照进行调色 0.引言 因科研等多场景需要进行绘图处理,笔者对PS进行了学习,本文通过《Photoshop2021入门教程》及其…...

Flutter 组件抽取:日期(DatePicker)、时间(TimePicker)弹窗选择器【仿照】
简介 仿照《Flutter 仿ios自定义一个DatePicker》实行的日期弹窗选择器(DatePicker)、时间弹窗选择器(TimePicker) 效果 范例 class _TestPageState extends State<TestPage> {overridevoid initState() {super.initStat…...

基于opencv的YOLOV3对图片的目标检测
目录 1. 准备工作 2. utils 函数 2.1 plot_show 函数 2.2 get_prediction 函数 2.3 draw_bounding_box 绘制边界框函数...

Mermaid流程图
所有流程图都由节点,几何形状和边缘,箭头或线条组成。mermaid代码定义了这些节点和边缘的制作和交互方式。 它还可以容纳不同的箭头类型、多方向箭头以及与子图之间的链接。 1、流程图的方向 TB - 从上到下TD - 自上而下/与上到下相同BT - 从下到上RL -…...

国产!全志科技T507-H工业核心板( 4核ARM Cortex-A5)规格书
1核心板简介 创龙科技 SOM-TLT507 是一款基于全志科技 T507-H 处理器设计的 4 核 ARM Cortex-A 53 全国产工业核心板,主频高达 1.416GHz 。核心板 CPU 、ROM 、RAM、电源、晶振等所有元器件均采用国产工业级方案,国产化率 100%。 核心板通过邮票孔连接方式引出 MIPI CSI 、…...

java小记 2023-05-05
public class Test {/*** 谓类的方法就是指类中用static 修饰的方法(非static 为实例方法),比如main 方法,那么可以以main* 方法为例,可直接调用其他类方法,必须通过实例调用实例方法,this 关键…...

CentOS安装Nginx
准备工作 在安装Nginx之前,我们需要进行一些准备工作: 确认系统是否已经安装了Nginx。如果已经安装了,需要卸载掉旧版本。安装EPEL源,以获取Nginx的软件包。安装必要的依赖软件包。 卸载旧版Nginx 如果已经安装了旧版本的Ngin…...
)
CSS布局基础(CSS书写顺序 导航栏写法 常见问题)
CSS布局基础(CSS书写顺序 & 导航栏写法) CSS布局基础(CSS书写顺序)导航栏写法PC端网页开发一般步骤容易出问题的点 CSS布局基础(CSS书写顺序) 布局定位属性自身属性(宽高,边框&…...

打造卓越 QML 层级设计:从入门到精通
目录标题 引言:QML 层级设计的重要性1.1 什么是 QML1.2 层级设计的核心理念1.3 实际应用案例 QML 基础知识2.1 语言概述2.2 基本元素2.3 属性和信号 设计原则与规范3.1 命名规范3.1.1 标识符命名3.1.2 文件命名3.1.3 文件夹命名 3.2 代码风格3.2.1 缩进与空格3.2.2 …...
shell流程控制之条件判断练习
1、判断当前磁盘剩余空间是否有20G,如果小于20G,则将报警邮件发送给管理员,每天检查一次磁盘剩余空间。 因为如果磁盘剩余空间小于20G需要报警发送邮件给管理员,所以需要对管理员的邮箱进行设置 (1)首先…...
linux中TF启动卡制作:磁盘分区文件同步
文章目录 前言:1. 连接TF卡2. 磁盘卸载载与分区2.1 磁盘卸载2.2 创建第一个分区2.3 创建第二个分区 3. 磁盘格式化4. 文件同步5. 检查与BOOT分区启动文件拷贝总结: 前言: TF卡在linux环境下配置好相关软件后,把配置好的系统以及软…...

【操作系统OS】学习笔记:第一章 操作系统基础【哈工大李治军老师】
基于本人观看学习 哈工大李治军老师主讲的操作系统课程 所做的笔记,仅进行交流分享。 特此鸣谢李治军老师,操作系统的神作! 如果本篇笔记帮助到了你,还请点赞 关注 支持一下 ♡>𖥦<)!! 主页专栏有更多࿰…...
)
Linux C/C++ 网络编程中地址格式转换(inet_pton和inet_ntop函数)
网络编程中地址格式转换(inet_pton和inet_ntop函数) 地址格式转换 #include <sys/types.h> #include <sys/socket.h> #include <arpa/inet.h>int inet_pton(int af , const char * src ,void * dst);(1…...
庖丁解牛函数知识---C语言《2》
目录 前言: 1.嵌套调用函数 2.链式访问 3.函数的声明与定义 4.*递归 5.递归与非递归 ❤博主CSDN:啊苏要学习 ▶专栏分类:C语言◀ C语言的学习,是为我们今后学习其它语言打好基础,C生万物! 开始我们的C语言之旅吧…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
