Windows11去掉不满足系统要求的提示水印
我的电脑是LEGION的拯救者R70002021，预装的是Windows 11 家庭中文版，没有折腾重装过系统，今天突然注意到右下角出现了这个提示：“不满足系统要求。转到’'设置"了解详细信息”。
在进入设置 - 系统 面板中也提示不满足系统要求，这你特么逗我呢？
虽然有这个水印也不影响系统的使用，但是这个提示又非常恶心，不知道情况的用户为了安全考虑，可能会重新去回退安装Windows10系统。
为什么会出现这个水印呢？
这可能是主板Bios中的的TPM模块没有被启用，所以系统检测不到该模块，生成了该提示。
微软为了提高系统的安全性，在Windows 11的安装要求上增加了TPM2.0这一项。
TPM 2.0于2015年在少量计算机上投入使用，并于2016年正式应用于计算机。如果需要将计算机系统更新到Windows 11，则需要检查计算机是否支持TPM 2.0。如果不支持，您的计算机将无法将系统更新到Windows 11；如果支持，请检查是否已禁用。如果已禁用，那么在升级过程中可能会导致Win11安装失败。
下面列出几个去除提示水印的方法：
方法 一
开启TPM模块，可以查找自己设备型号的Bios设定项，找到TPM功能将它启用，下面列出几个常见设备开启方式
Thinkpad开启TPM选项：
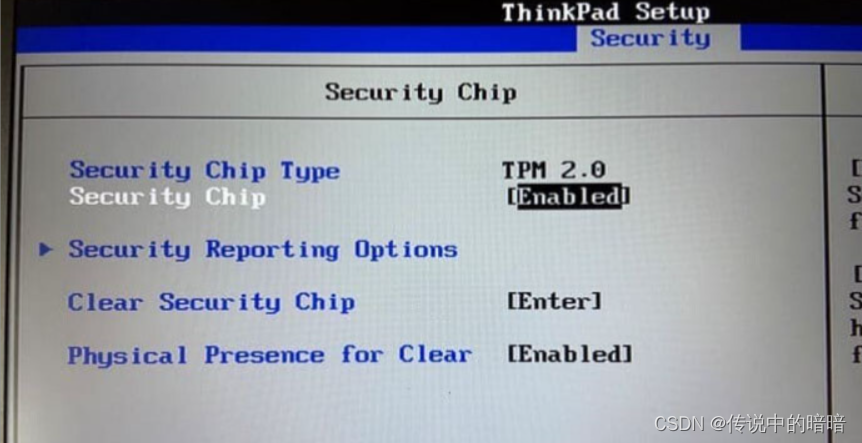
HP 开启TPM选项
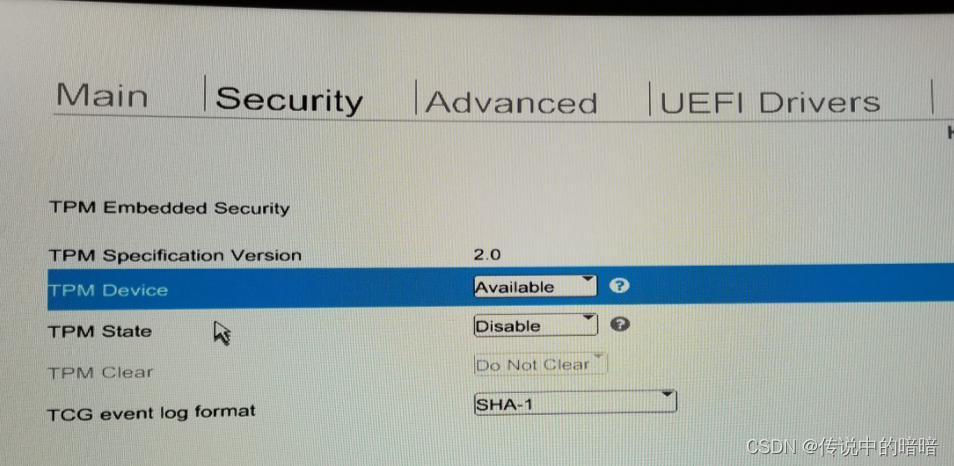
LEGION 开启TPM选项
AMD 的设备就是在安全选项中找到 AMD Platform Security Processor技术 这一项功能启用即可。
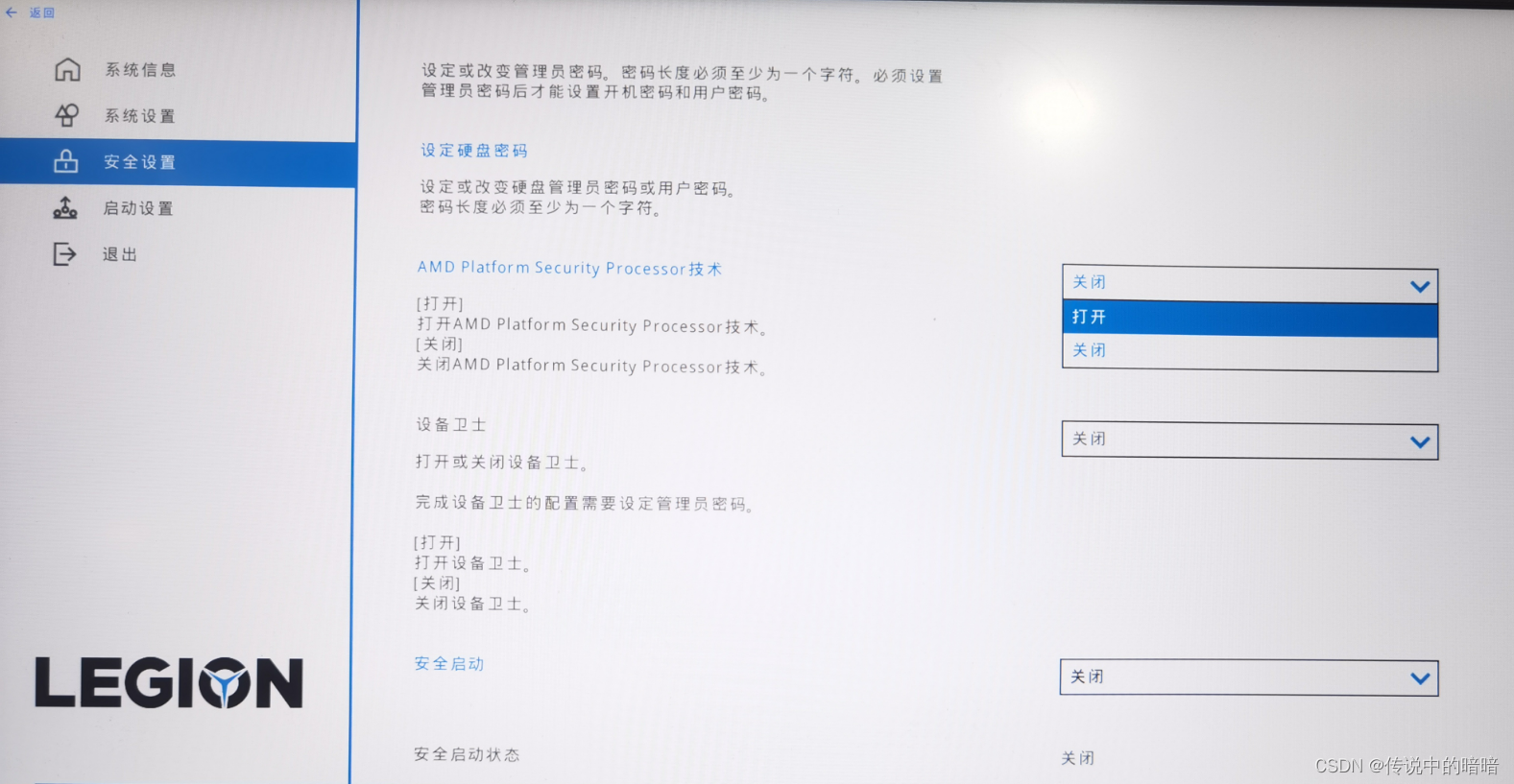
启用后，我们可以在设备管理器中找到受信任的平台模块2.0 未启用状态则不会显示这一项。
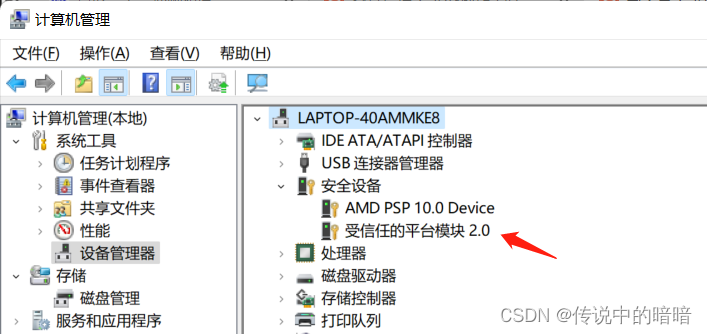
方法 二
如果不想启用TPM2.0或者没有TPM选项的童鞋，我们也可以通过修改注册表来关闭提示。
1、按 Win+R 输入 regedit 打开注册表编辑器。
2、导航到 \HKEY_CURRENT_USER\Control Panel\UnsupportedHardwareNotificationCache 或将其粘贴到地址栏中，然后按 Enter。
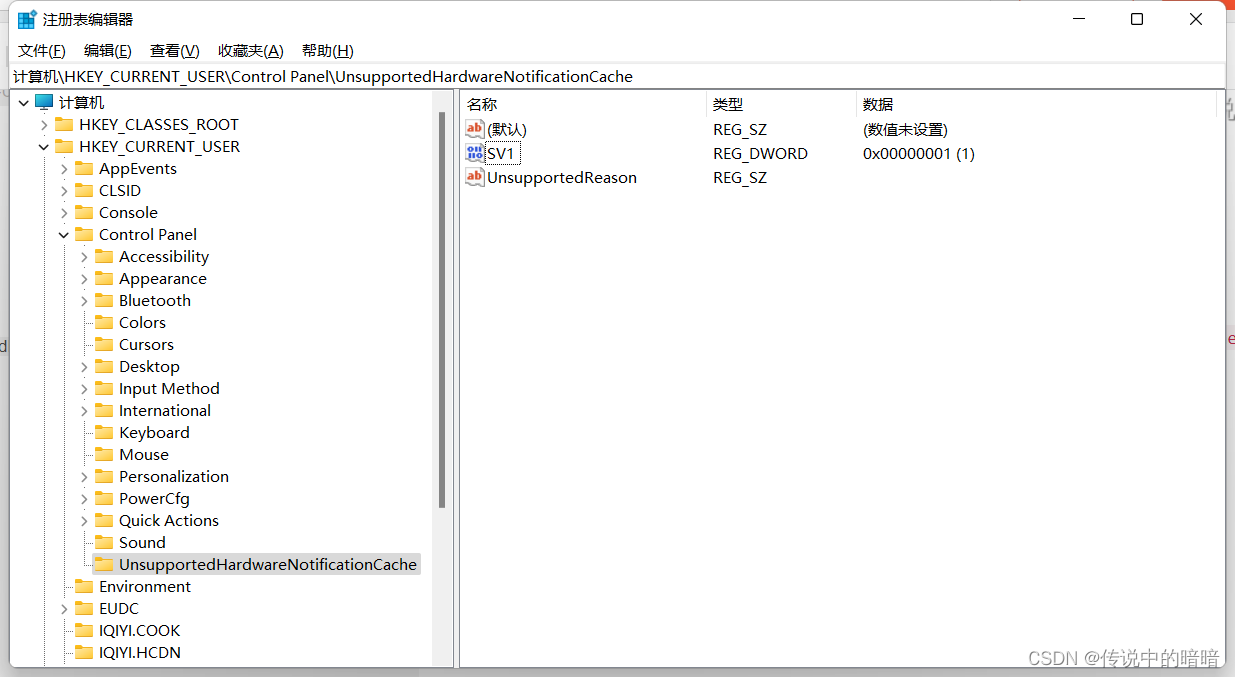
3、在右侧窗格中，将 SV1 的 Dword 值从 1 更改为 0，回到桌面，我们右键刷新桌面后提示就消失了。
方法 三
注册表命令修改
以管理员权限启动CMD后输入下面命令即可完成修改。
Reg add "HKEY_CURRENT_USER\Control Panel\UnsupportedHardwareNotificationCache" /v SV1 /t REG_DWORD /d 0 /f
相关文章：
Windows11去掉不满足系统要求的提示水印
我的电脑是LEGION的拯救者R70002021，预装的是Windows 11 家庭中文版，没有折腾重装过系统，今天突然注意到右下角出现了这个提示：“不满足系统要求。转到’设置"了解详细信息”。 在进入设置 - 系统 面板中也提示不满足系统要…...
JavaScript 计时事件
JavaScript 计时事件 通过使用 JavaScript，我们有能力做到在一个设定的时间间隔之后来执行代码，而不是在函数被调用后立即执行。我们称之为计时事件。 在 JavaScript 中使用计时事件是很容易的，两个关键方法是: setInterval() - 间隔指定的…...
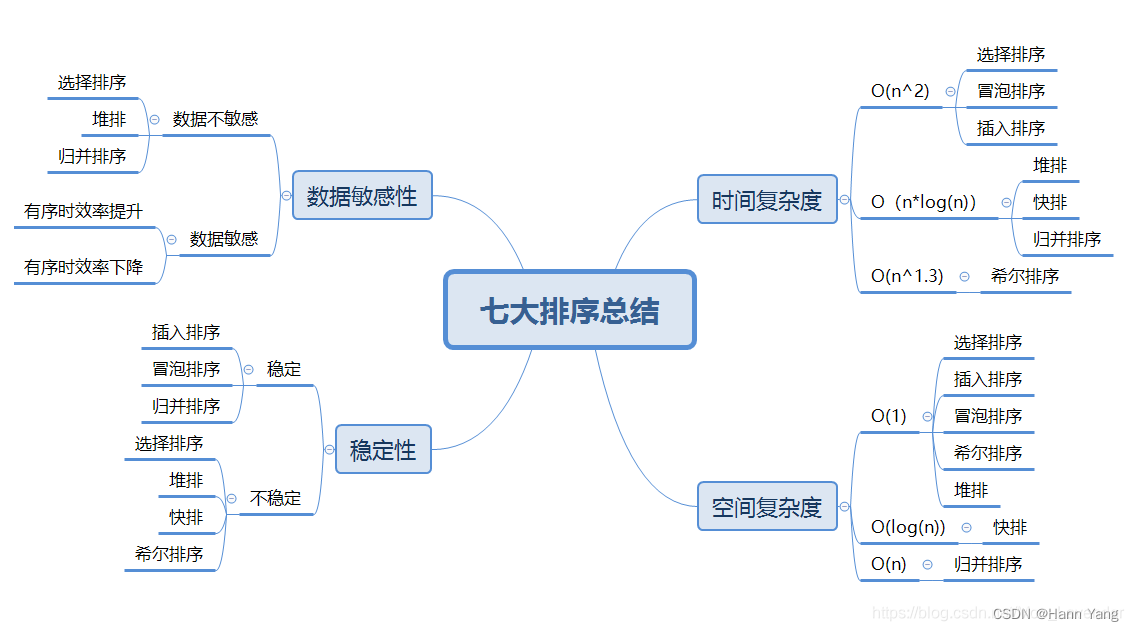
七大排序算法的多语言代码实现
文章目录 前言 一、排序算法 1.原理简述 2.分类与复杂度 二、实例代码 1.冒泡排序 C Python Java Golang Rust Dephi 2.选择排序 C Python Java Golang Rust Dephi 3.插入排序 C Python Java Golang Rust Dephi 4.希尔排序 编辑 C Python Java Gola…...
【基础算法】表达式计算
中缀表达式:我们平常见到的正常数学式子 后缀表达式：12-3* 后缀表达式对于计算机很容易计算，只需要从头部扫描字符串。然后遇到数字就入栈，遇到运算符就取出栈顶的两个数进行运算。最后把运算结果入栈，最后栈中就会剩一个数为答…...
动态规划问题
目录 一、动态规划简介 二、利用动态规划解决问题 1、斐波拉契序列 2、拆分词句 3、三角形最小路径和 4、不同的路径数目（一） 5、带权值的最小路径和 6、求路径ii 7、01背包 8、不同子序列 9、编辑距离 10、分割回文串 一、动态规划…...
【MySQL进阶】 存储引擎 索引
😊😊作者简介😊😊 ： 大家好，我是南瓜籽，一个在校大二学生，我将会持续分享Java相关知识。 🎉🎉个人主页🎉🎉 ： 南瓜籽的主页…...
5 款最好的免费 SSD 数据恢复软件
SSD（固态硬盘）提供比传统硬盘更快的读/写速度，使启动、软件加载和游戏启动更快。因此，在我们选择存储设备时，它是一个极好的选择。但是，它仍然存在数据丢失的风险。假设您是受害者之一，正在寻找…...
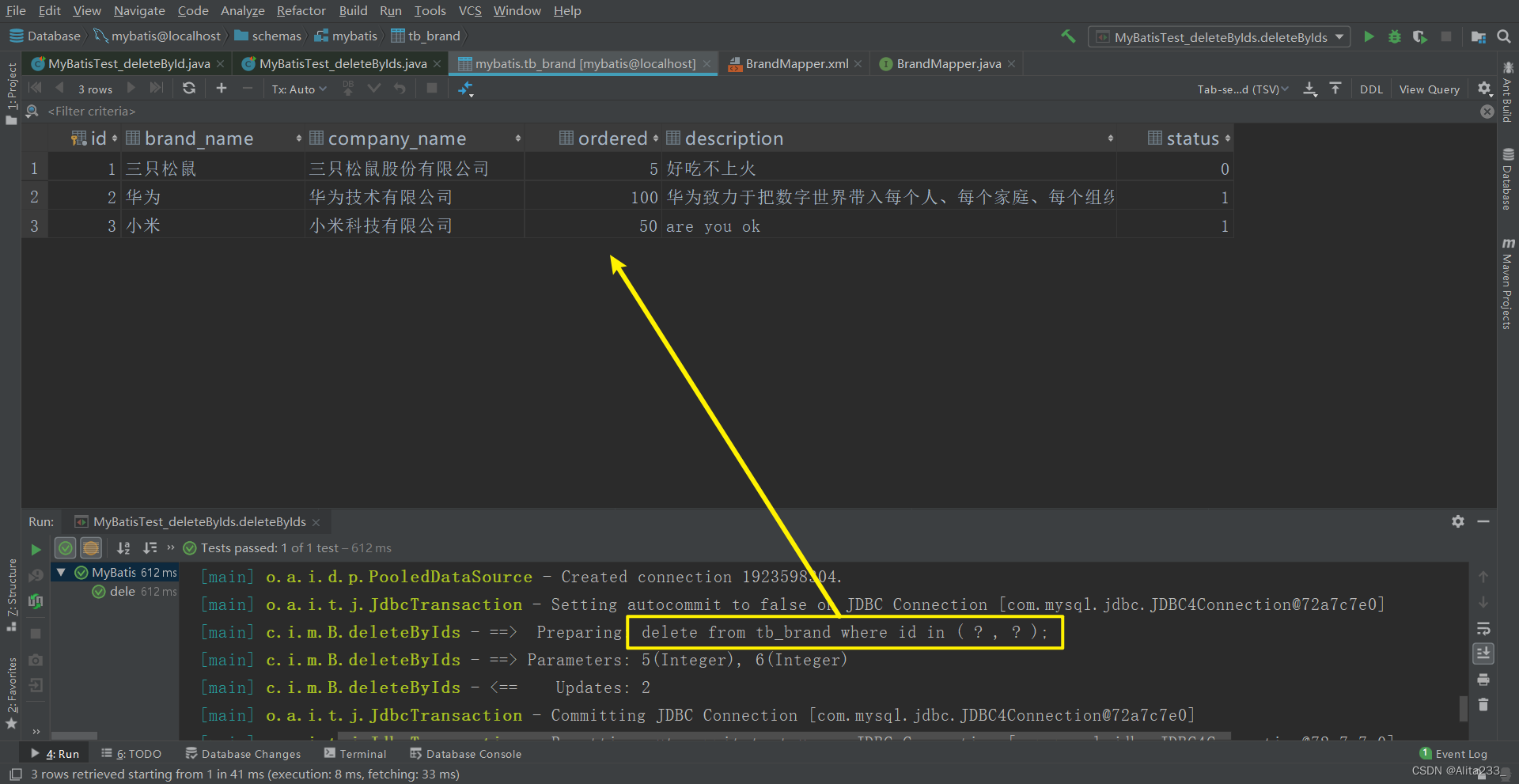
MyBatis案例 | 使用映射配置文件实现CRUD操作——删除数据
本专栏主要是记录学习完JavaSE后学习JavaWeb部分的一些知识点总结以及遇到的一些问题等，如果刚开始学习Java的小伙伴可以点击下方连接查看专栏 本专栏地址：🔥JavaWeb Java入门篇： 🔥Java基础学习篇 Java进阶学习篇&…...
CSDN 编程竞赛二十八期题解
竞赛总览 CSDN 编程竞赛二十八期：比赛详情 (csdn.net) 本期竞赛的题目都很简单，但是非常考验读题和编码速度。这一次没有遇到bug，竞赛体验较好。 竞赛题解 题目1、小Q的鲜榨柠檬汁 团建活动是大家所想要的。小Q给大家准备了鲜橙汁。现在…...
DML数据操纵语言
DML数据操纵语言 目录概述一、插入语句(一)方式一(二)方式二：(三)两种方式的比较二、修改语句三、删除语句概述方式一：delete方式二：truncate语句 【清空语句】delete VS truncate 【面试题！！！】概述 数据…...
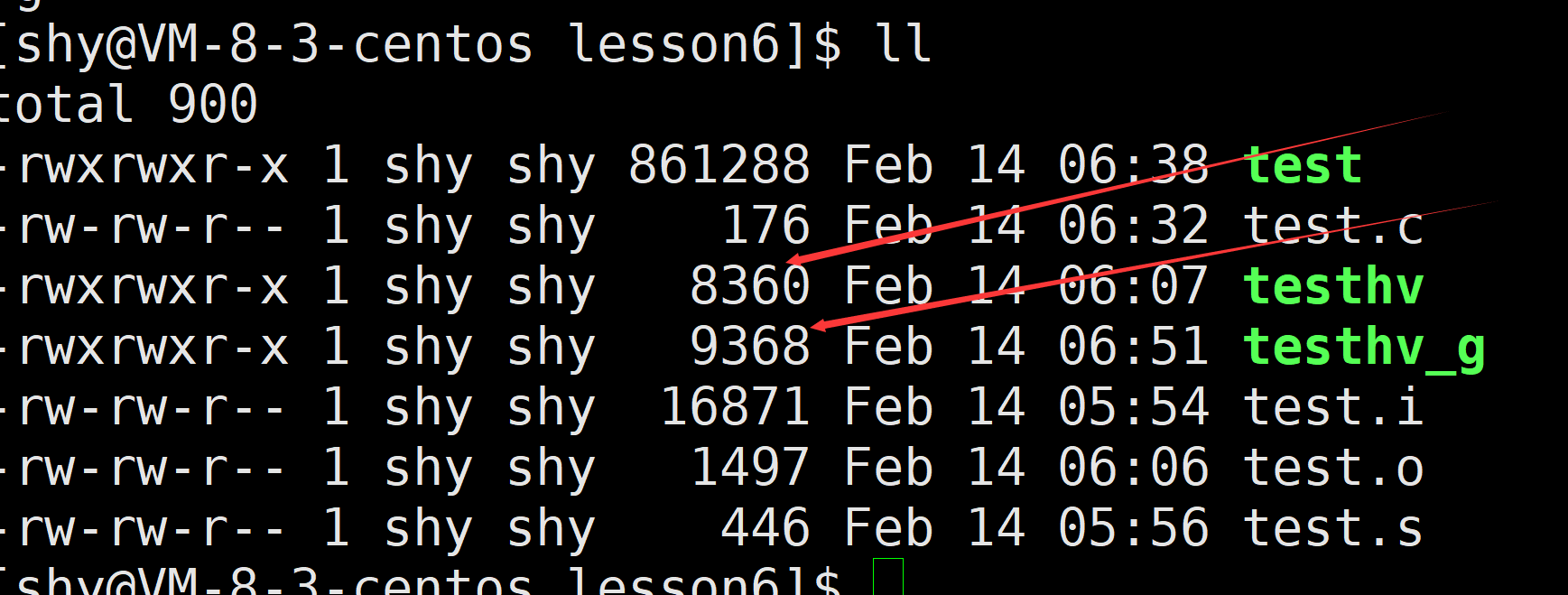
【Hello Linux】Linux工具介绍 （gcc/g++ gdb）
作者：小萌新 专栏：Linux 作者简介：大二学生 希望能和大家一起进步！ 本篇博客简介：介绍Linux的常用工具gcc/g 以及gbd Linux工具介绍gcc / ggcc / g的作用为什么语言要经过这四步才能变为可执行指令gcc / g语法预处理编…...
TeamFiltration：一款针对O365 AAD账号安全的测试框架
关于TeamFiltration TeamFiltration是一款针对O365 AAD账号安全的跨平台安全测试框架，在该工具的帮助下，广大研究人员可以轻松对O365 AAD账号进行枚举、喷射、过滤和后门植入等操作。TeamFiltering与CrackMapExec非常相似，它可以创建并维护一…...
你是真的“C”——Visual Studio 2022（VS2022）编译器 -—实用调试技巧
你是真的“C”——Visual Studio 2022（VS2022）编译器 -—实用调试技巧😎前言🙌1. 什么是bug？🙌2. 调试是什么？有多重要？🙌2.1 调试是什么？2.2 调试的基本步骤…...
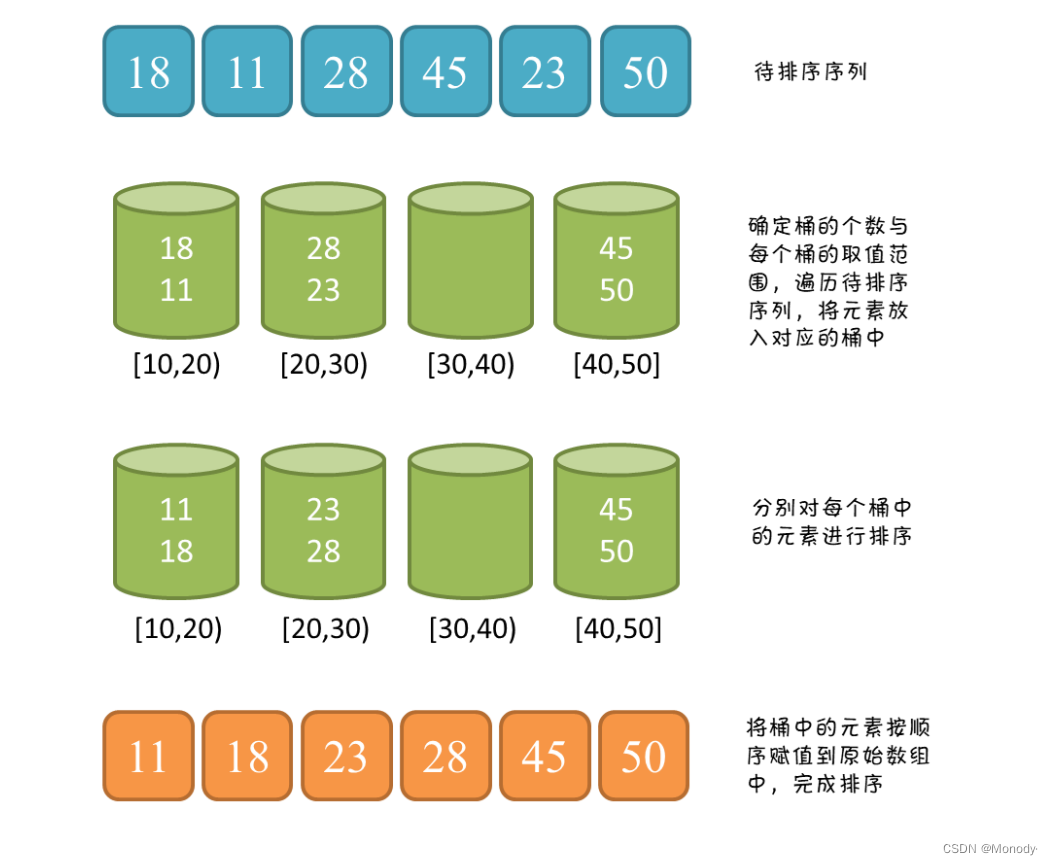
数据结构与算法：7种必须会的排序以及3种非基于比较排序
1.什么是排序 排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。 稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序…...
数据库用户数
Oracle的用户数 oracle软件内部并没对用户数做限制，买5个用户数，指你买了5个user licences，从法律上只能连5个session，超过5个的连接都是非法的。oracle不给你技术上的限制，可是给你法律上的限制。 一般来讲…...
nginx如何用html显示多个图片并加入播放链接
需求背景通过nginx来做个点播服务，ffmpeg截取视频中的某一帧作为视频的封面，前端页面展示这个封面，，并链接到对应的视频播放链接，加载播放器进行播放简单介绍一下ffmpeg截取视频中的某一帧的方式截取视频的第一帧&…...
【蓝桥杯集训·每日一题】Acwing 3729. 改变数组元素
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一维差分区间合并一、题目 1、原题链接 3729. 改变数组元素 2、题目描述 给定一个空数组 V 和一个整数数组 a1,a2,…,an。 现在要对数组 V 进行 n 次操作。 第 i 次操作的…...
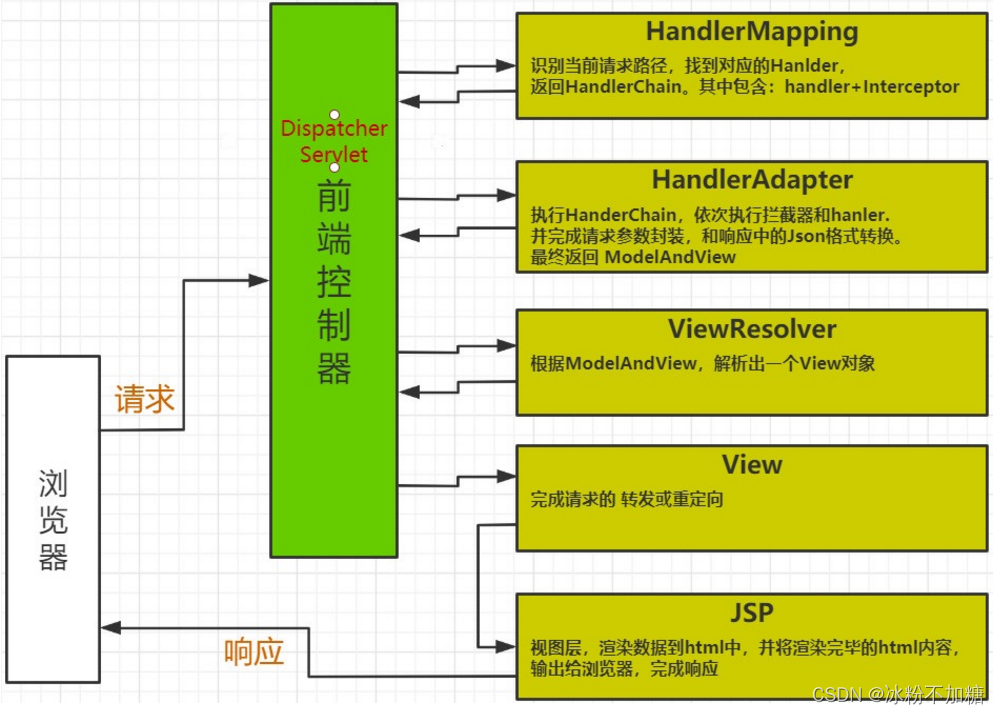
springmvc执行流程
文章目录前言一、springMVC请求执行流程二、组件说明以下组件通常使用框架提供实现：总结前言 本篇文章是对springmvc的补充 接上篇文章springmvc入门https://blog.csdn.net/l_zl2021/article/details/127120873 一、springMVC请求执行流程 1.用户发送请求至前端控制…...
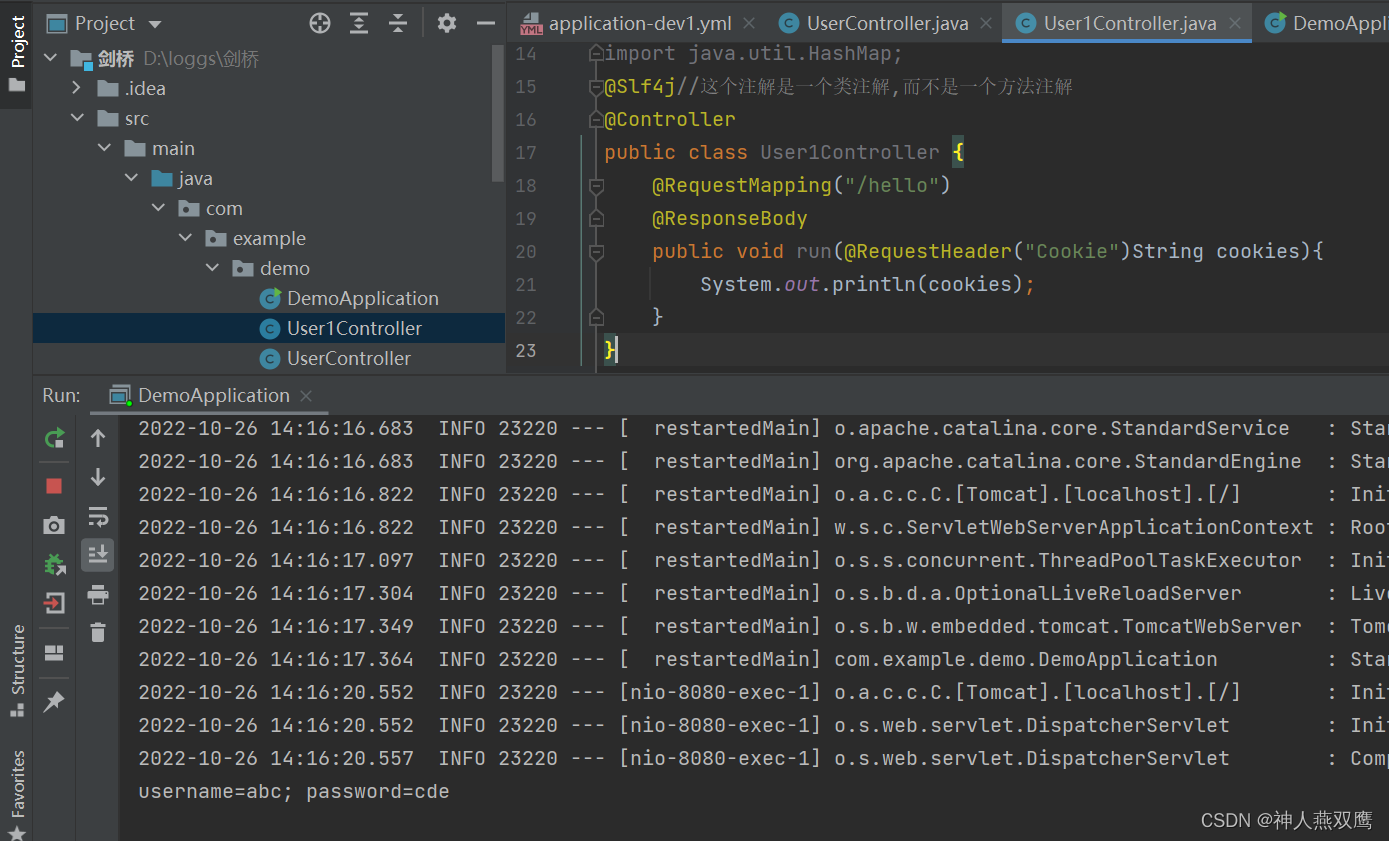
SpringMVC(2)
一)接受到JSON格式的数据:使用RequestBody来进行接收 ResponseBody表示的是返回一个非页面的数据 RequestBody表示的是后端要接受JSON格式的数据 一)接收单个格式的JSON格式的数据，我们使用一个对象来进行接收 1)我们之前接受GET请求中的queryString中的参数的时候&…...
Jackson序列化json时null转成空串或空对象
在项目中可能会遇到需要将null转""，可以通过以下方法解决。一：添加JacksonConfig 配置import com.fasterxml.jackson.core.JsonGenerator;import com.fasterxml.jackson.databind.JsonSerializer;import com.fasterxml.jackson.databind.Objec…...
深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架，用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录，以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现，玩家控制一个角色（龙）躲避障碍物（仙人掌和乌鸦）。以下是代码的详细介绍：…...
反向工程与模型迁移：打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下，商品详情API作为连接电商平台与开发者、商家及用户的关键纽带，其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息（如名称、价格、库存等）的获取与展示，已难以满足市场对个性化、智能…...
【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成：MAC头部frame bodyFCS，其中MAC是固定格式的，frame body是可变长度。 MAC头部有frame control，duration，address1，address2，addre…...
Mybatis逆向工程，动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢，博主的学习进度也是步入了Java Mybatis 框架，目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学，希望能对大家有所帮助，也特别欢迎大家指点不足之处，小生很乐意接受正确的建议&…...
SpringCloudGateway 自定义局部过滤器
场景： 将所有请求转化为同一路径请求（方便穿网配置）在请求头内标识原来路径，然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
Unity | AmplifyShaderEditor插件基础（第七集：平面波动shader）
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中，CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时，通常会导致应用响应缓慢，甚至服务不可用，严重影响用户体验和业务运行。因此，掌握一套科学有效的CPU飙高问题排查方法&…...
LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录，不允许匿名访问，kefu只能访问/data/kefu目录，不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时，会出现小数部分被截断的情况。典型错误模式如下： void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...