洛谷 子集积 题解
题目
P1 背包
子集积 > m >m >m 个数并不好求,考虑子集积 ≤ m \le m ≤m 的个数 x x x,答案即为 ( 2 n − x ) (2^n - x) (2n−x)。
对于子集积 ≤ m \le m ≤m 的个数,可以化为 0-1 背包问题做, f i , j f_{i,j} fi,j 表示前 i i i 个数,子集积为 j j j 的个数,有:
f i , j = ∑ j = 1 m f i − 1 , j a i f_{i,j}=\sum \limits_{j=1}^{m} f_{i-1,\frac {j} {a_i}} fi,j=j=1∑mfi−1,aij ( j j j 是 a i a_i ai 的倍数)。
背包问题常规地去掉一维: f j f_j fj 表示子集积为 j j j 的个数:
f j = ∑ j = 1 m f j a i f_j=\sum \limits_{j=1}^{m} f_{\frac {j} {a_i}} fj=j=1∑mfaij ( j j j 是 a i a_i ai 的倍数)。
cin >> n >> m;for(int i=1; i<=n; i++) cin >> a[i];f[1] = 1;for(int i=1; i<=n; i++)for(int j=(m / a[i]) * a[i]; j>=a[i]; j-=a[i])f[j] += f[j / a[i]], f[j] %= mod;int sum = qpow(2, n);for(int i=1; i<=m; i++)sum -= f[i], sum = ((sum % mod) + mod) % mod;cout << sum;
时间复杂度 O ( n × ∑ i = 1 n m a i ) O(n \times \sum\limits_{i=1}^{n} {\frac {m} {a_i}}) O(n×i=1∑naim) ,最坏情况下 O ( n m ) O(nm) O(nm) 。
P2 优化
优化 1
若序列中有 100 100 100 个 1 1 1 ,然而任意多个 1 1 1 不会对子集积产生影响,我们只需要在方案数中乘以 2 100 2^{100} 2100 即可。
...int sum = qpow(2, n);for(int i=1; i<=m; i++)sum -= (f[i] * qpow(2, cnt[1])) % mod, sum = ((sum % mod) + mod) % mod;cout << sum;
优化 2
时间复杂度高的原因在于重复的计算:若有 100 100 100 个 2 2 2 ,我们会将第 2 , 3 2,3 2,3 个 2 2 2 、第 3 , 4 3,4 3,4 个 2 2 2 算了两次。我们应该只关心是几个 2 2 2 ,而不关心是哪几个 2 2 2。
对于任意一个数 x x x ,设其出现了 t t t 次,我们可以对 x 1 , x 2 , . . . , x t x^1,x^2,...,x^t x1,x2,...,xt 分别计算,使用 x i x^i xi 计算贡献时乘以 C t i C_{t}^i Cti, 即 :
f j = ∑ i = 1 t ( f j x i × C t i ) f_j=\sum\limits_{i=1}^{t} ( f_{\frac {j} {x^i}} \times C_t^i) fj=i=1∑t(fxij×Cti) ( j j j 是 x k x^k xk 的倍数)。
时间复杂度 O ( n ∑ i = 1 n ( log a i m ) ) O(n \sum\limits_{i=1}^{n} (\log_{a_i}{m})) O(ni=1∑n(logaim)),最坏情况下 O ( n log m ) O(n \log m) O(nlogm)。
注意: 这里与多重背包的二进制拆分拆成多个物品不同,而是优化了对于一个物品的计算方式。
代码
相关文章:

洛谷 子集积 题解
题目 P1 背包 子集积 > m >m >m 个数并不好求,考虑子集积 ≤ m \le m ≤m 的个数 x x x,答案即为 ( 2 n − x ) (2^n - x) (2n−x)。 对于子集积 ≤ m \le m ≤m 的个数,可以化为 0-1 背包问题做, f i , j f_{i,…...

Boost笔记 1:下载、编译、安装、测试
1. 下载 当前版本是1.82,下载链接: https://boostorg.jfrog.io/artifactory/main/release/1.82.0/source/ 2. 安装编译依赖库 本地环境是Ubuntu 22.04,需要安装以下依赖库,部分影响boost相关功能的开启,部分影响编译…...

tiechui_lesson01_入口函数和卸载函数
主要讲解入口函数和卸载函数。 #include <ntifs.h>VOID nothing(HANDLE ppid, HANDLE mypid, BOOLEAN bcreate) {UNREFERENCED_PARAMETER(ppid);UNREFERENCED_PARAMETER(mypid);UNREFERENCED_PARAMETER(bcreate);DbgPrint("processNotify\n"); }VOID DriverU…...

密码学【java】初探究加密方式之非对称加密
文章目录 非对称加密1 常见算法2 生成公钥和私钥3 私钥加密4 私钥加密 公钥解密5 公钥和私钥的保存和读取5.1 **保存公钥和私钥**5.2 读取公钥和私钥 非对称加密 非对称加密算法又称现代加密算法。非对称加密是计算机通信安全的基石,保证了加密数据不会被破解。与对…...

网络安全和黑客技能:15本必读书籍推荐
前言 网络安全和黑客技能紧密相连。想要有效地防范黑客攻击,了解黑客的技能和思维方式非常重要。而要想成为一名合格的白帽黑客,也需要深入理解网络安全的基本原理和最佳实践。本文将介绍15本网络安全和黑客书籍,既包括了防范黑客攻击的指南…...

电话号码的字母组合
题目:17. 电话号码的字母组合 - 力扣(Leetcode) 思路: 给定一个电话号码字符串 digits,须输出它所能表示的所有字母组合。我们可以先定义一个数字字符到字母表的映射表 numToStr,然后再用 Combine 函数递归…...
PAT A1032 Sharing
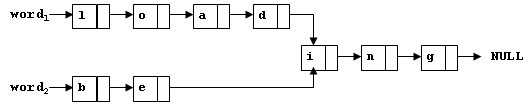
1032 Sharing 分数 25 作者 CHEN, Yue 单位 浙江大学 To store English words, one method is to use linked lists and store a word letter by letter. To save some space, we may let the words share the same sublist if they share the same suffix. For example, l…...

Git常见问题汇总
问题:Your branch is ahead of ‘origin/master’ by 1 commit 原因:你的本地分支高于远程仓库一次提交, 同步更新下,执行命令: git push origin master问题:warning: LF will be replaced by CRLF in main.lua The …...

设计模式之代理模式(静态代理动态代理)
目录 1、什么是代理模式 2、代理模式的结构 3、代理模式的实现 3.1 静态代理和动态代理概念 3.2 静态代理 3.3 动态搭理 3.3.1 代码实现 3.3.2 Proxy类讲解 4、动态代理VS静态代理 5、代理模式优缺点 1、什么是代理模式 由于某些原因需要给某对象提供一个代理以控制对…...

Java并发编程基础知识概述
前言 在现代计算机系统和服务器中,多线程并行执行已经成为常态,而且并发编程能够充分利用系统资源,提高程序处理效率和质量。因此,Java并发编程是Java程序员必须掌握的重要技能之一。 线程和进程 在操作系统中,进程是…...
Redis超详细入门手册教程!还不快来看看?
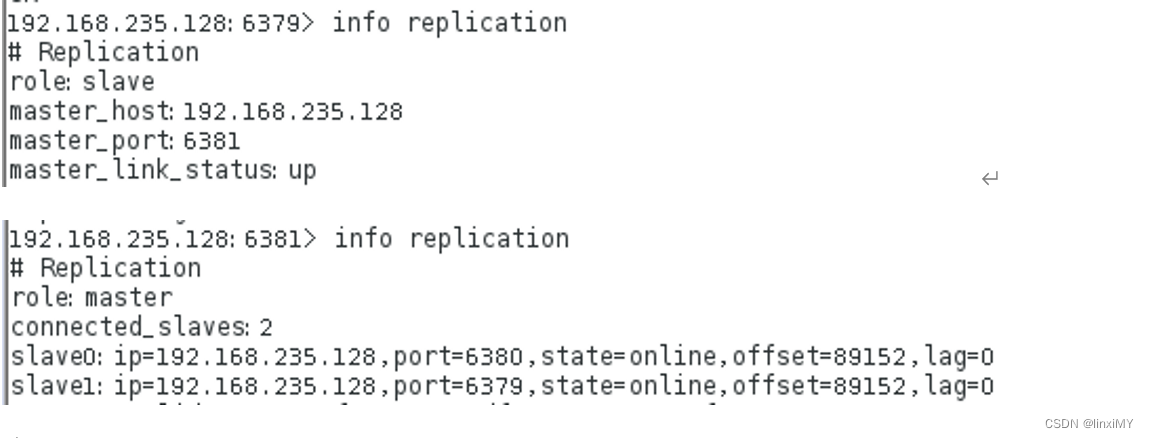
地址: RedisRedis is an open source (BSD licensed), in-memory data structure store, used as a database, cache, and message broker. Redis provides data structures …https://redis.io/ 1:NoSQL简介 1.1:数据库应用的演变历程 单…...
代码随想录算法训练营第四十九天| 121. 买卖股票的最佳时机、122.买卖股票的最佳时机II
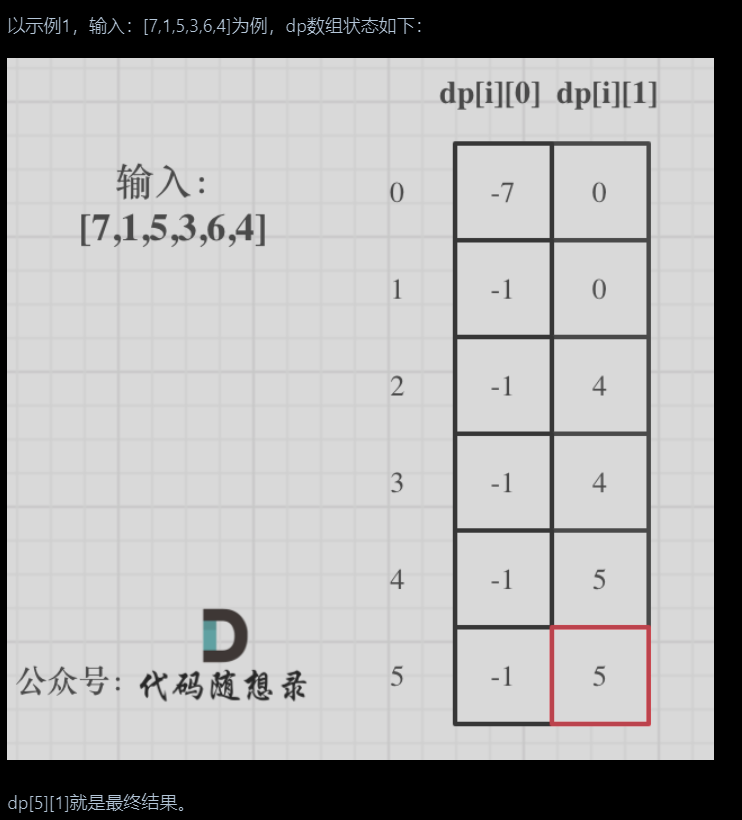
文章目录 121. 买卖股票的最佳时机122.买卖股票的最佳时机II 121. 买卖股票的最佳时机 为什么定义dp数组为二维数组? dp数组定义,dp(i)[0] 表示第i天持有股票所得最多现金,dp(i)[1]表示第i天不持有股票的状态(未必当前卖出&#x…...

零基础如何学习挖漏洞?看这篇就够了【网络安全】
前言 有不少阅读过我文章的伙伴都知道,我从事网络安全行业已经好几年,积累了丰富的经验和技能。在这段时间里,我参与了多个实际项目的规划和实施,成功防范了各种网络攻击和漏洞利用,提高了安全防护水平。 也有很多小…...

Twitter 推荐算法底有多牛? 已斩获11.7K star
点击上方“Github中文社区”,关注 看Github,每天提升第070期分享 ,作者:Huber | Github中文社区 大家好,我是Huber。 在美国当地时间 3 月 31 日,马斯克履行当初的诺言,他宣布了 Twitter 算法的…...
看过这篇文章,读懂数据分析
一、为什么需要数据分析 数据分析的重要性不言而喻,没有数据,就是感性。数据不会被观点打败,数据只能被数据打败。我们现在妥妥地已经进入了数据时代。 量化IT投资成效,以数据驱动决策 站在公司或者决策者角度,数据最…...

[计算机图形学]光场,颜色与感知(前瞻预习/复习回顾)
一、Light Field / Lumigraph—光场 1.我们看到的是什么 我们的眼睛能够把3D世界转换为2D的成像信号被我们感知,如上面第一幅图,这就是我们看到整个世界的过程,那么如果我们把之前记录的光的信息都完美的放在一个幕布上,那么我们…...

L4公司进军辅助驾驶,放话无图也能跑遍中国
作者 | Amy 编辑 | 德新 高阶智能驾驶走向规模量产,高精地图成为关键的门槛之一。今年,多家车企和智驾公司都喊出「不依赖高精地图,快速大规模落地」的口号。 华为、小鹏、元戎以及毫末等,可能是最快在国内量产 无高精图智…...

【Java笔试强训 17】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥杨辉三角…...
【IPv6】基本概念及字段
IPV4知识点: 字段值 IPv4字段共 字段值解释Version版本版本字段,可以区分V4和V6版本,V4是0100,V6是0110,需要注意的是V4和V6头部除了版本字段位置相同外,其他都是不一样的,因此两个协议不能直…...

数据库中的 Schema 变更实现
线上沙龙-技术流第 30 期营业啦 05月09日(周二)19:30 KaiwuDB - B站直播间 传统数据库操作 Schema 变更时,第一步便是锁表,需持续到 Schema 变更操作完成。这样的做法虽然实现简单,无需考虑事务并发带来的影响&#…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
