【VAR模型 | 时间序列】帮助文档:VAR模型的引入和Python实践(含源代码)
向量自回归 (VAR) 是一种随机过程模型,用于捕获多个时间序列之间的线性相互依赖性。 VAR 模型通过允许多个进化变量来概括单变量自回归模型(AR 模型)。
VAR 中的所有变量都以相同的方式进入模型:每个变量都有一个方程式,根据其自身的滞后值、其他模型变量的滞后值和一个误差项来解释其演变。
文章目录
- 一、简介
- 二、VAR模型公式背后的直觉
- 三、在Python中构建VAR模型
- 3.1 导包
- 3.2 导入数据集
- 3.3 可视化时间序列
- 3.4 使用格兰杰因果关系检验检验因果关系
- 3.5 协整测试
- 3.6 将序列拆分为训练数据和测试数据
- 3.7 检查平稳性并使时间序列保持平稳
- 3.8 如何选择VAR模型的阶数(P)
- 3.9 训练选定订单的VAR模型(p)
- 3.10 使用德宾沃森统计量检查残差(误差)的序列相关性
- 3.11 如何使用统计模型预测VAR模型
- 3.12 反转变换以获得真实预测
- 3.13 预测与实际图
- 3.14 评估预测
一、简介
首先,什么是向量自回归(VAR)以及何时使用它?
向量自回归 (VAR) 是一种多变量预测算法,当两个或多个时间序列相互影响时使用。
这意味着,使用 VAR 的基本要求是:
- 至少需要两个时间序列(变量);
- 时间序列应相互影响。
好。那么为什么它被称为“自回归”呢?
它被认为是自回归模型,因为每个变量(时间序列)都建模为过去值的函数,即预测变量只不过是序列的滞后(时间延迟值)。
好的,那么VAR与其他自回归模型(如AR,ARMA或ARIMA)有何不同?
主要区别在于这些模型是单向的,其中预测变量影响 Y,反之亦然。而矢量自动回归 (VAR) 是双向的。也就是说,变量相互影响。
二、VAR模型公式背后的直觉
在自回归模型中,时间序列被建模为其自身滞后的线性组合。也就是说,序列的过去值用于预测当前和未来。
典型的 AR(p) 模型方程如下所示:
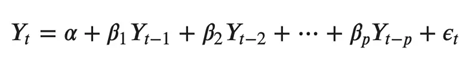
其中α是截距,一个常数,β1,β2 直到 βp 是 Y 到 p 阶的滞后的系数。阶“p”表示,最多使用 Y 的 p 滞后,它们是方程中的预测因子。ε_{t}是错误,被视为白噪声。
好。那么,VAR模型的公式是什么样的呢?
在VAR模型中,每个变量都被建模为自身过去值和系统中其他变量过去值的线性组合。由于我们有多个相互影响的时间序列,因此将其建模为方程组,每个变量(时间序列)一个方程。
也就是说,如果有5个相互影响的时间序列,我们将拥有一个由5个方程组成的系统。
那么,方程是如何精确构建的?
假设我们有两个变量(时间序列)Y1 和 Y2,需要在时间(t)预测这些变量的值。
为了计算Y1(t),VAR将使用Y1和Y2的过去值。同样,要计算 Y2(t),请使用 Y1 和 Y2 的过去值。
例如,具有两个时间序列(变量“Y1”和“Y1”)的 VAR(2) 模型的方程组如下:
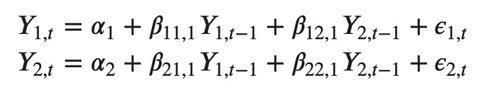
其中,Y{1,t-1} 和 Y{2,t-1} 分别是时间序列 Y1 和 Y2 的第一个滞后。
上述方程称为 VAR(1) 模型,因为每个方程的阶数为 1,也就是说,它最多包含一个预测变量(Y1 和 Y2)的滞后。
由于方程中的 Y 项是相互关联的,因此 Y 被视为内生变量,而不是外生预测因子。
类似地,两个变量的二阶 VAR(2) 模型将为每个变量(Y1 和 Y2)包含最多两个滞后。
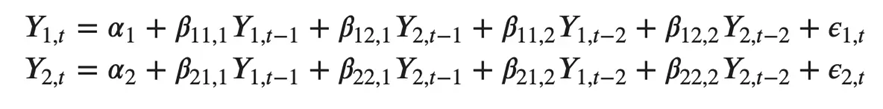
能想象一个有三个变量(Y2、Y1和Y2)的二阶VAR(3)模型会是:
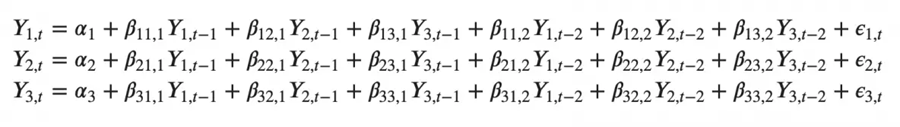
随着模型中时间序列(变量)数量的增加,方程组会变大。
三、在Python中构建VAR模型
构建 VAR 模型的过程涉及以下步骤:
- 分析时间序列特征
- 检验时间序列之间的因果关系
- 平稳性测试
- 如果需要,转换序列以使其静止
- 找到最佳顺序 (p)
- 准备训练和测试数据集
- 训练模型
- 回滚转换(如果有)
- 使用测试集评估模型
- 对未来的预测
3.1 导包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline# Import Statsmodels
from statsmodels.tsa.api import VAR
from statsmodels.tsa.stattools import adfuller
from statsmodels.tools.eval_measures import rmse, aic
3.2 导入数据集
使用Yash P Mehra在1994年的文章“工资增长和通货膨胀过程:一种实证方法”中使用的时间序列。
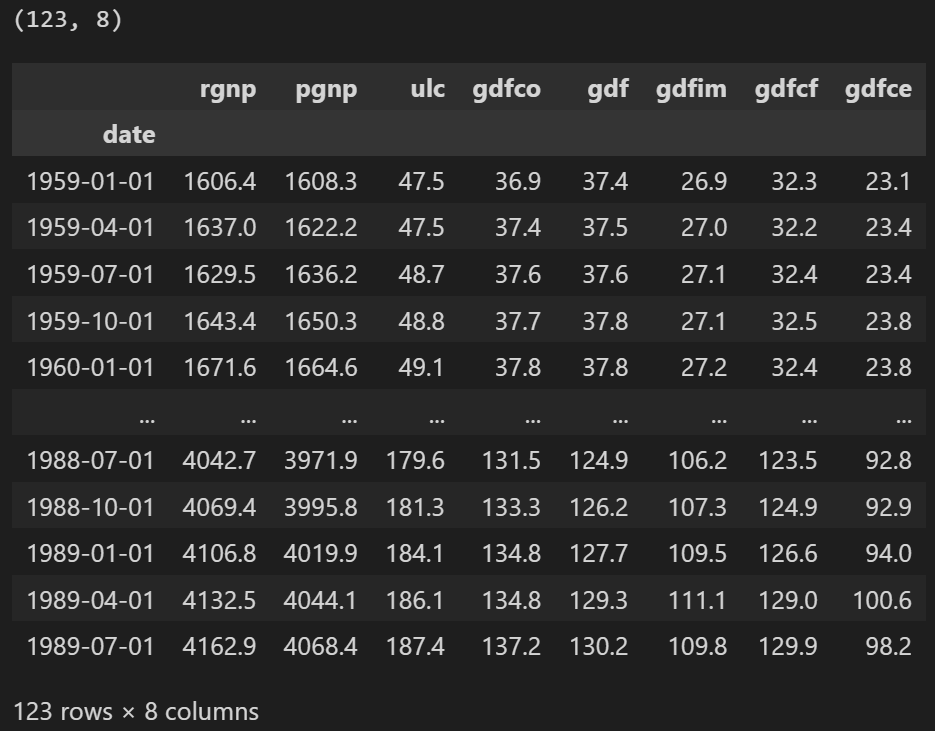
此数据集具有以下 8 个季度时间序列:
- rgnp : Real GNP.(实际国民生产总值)
- pgnp : Potential real GNP.(潜在实际国民生产总值)
- ulc : Unit labor cost.(单位人工成本)
- gdfco : Fixed weight deflator for personal consumption expenditure excluding food and energy.(不包括食品和能源的个人消费支出固定权重平减指数)
- gdf : Fixed weight GNP deflator.(固定权重国民生产总值平减指数)
- gdfim : Fixed weight import deflator.(固定重量进口平减指数)
- gdfcf : Fixed weight deflator for food in personal consumption expenditure.(个人消费支出中食品固定权重平减指数)
- gdfce : Fixed weight deflator for energy in personal consumption expenditure.(个人消费支出能源固定权重平减指数)
filepath = 'https://raw.githubusercontent.com/selva86/datasets/master/Raotbl6.csv'
df = pd.read_csv(filepath, parse_dates = ['date'], index_col = 'date')
print(df.shape)
df
3.3 可视化时间序列
fig, axes = plt.subplots(nrows=4, ncols=2, dpi=120, figsize=(10,6))
for i, ax in enumerate(axes.flatten()):data = df[df.columns[i]]ax.plot(data, color='red', linewidth=1)# Decorationsax.set_title(df.columns[i])ax.xaxis.set_ticks_position('none')ax.yaxis.set_ticks_position('none')ax.spines["top"].set_alpha(0)ax.tick_params(labelsize=6)plt.tight_layout()
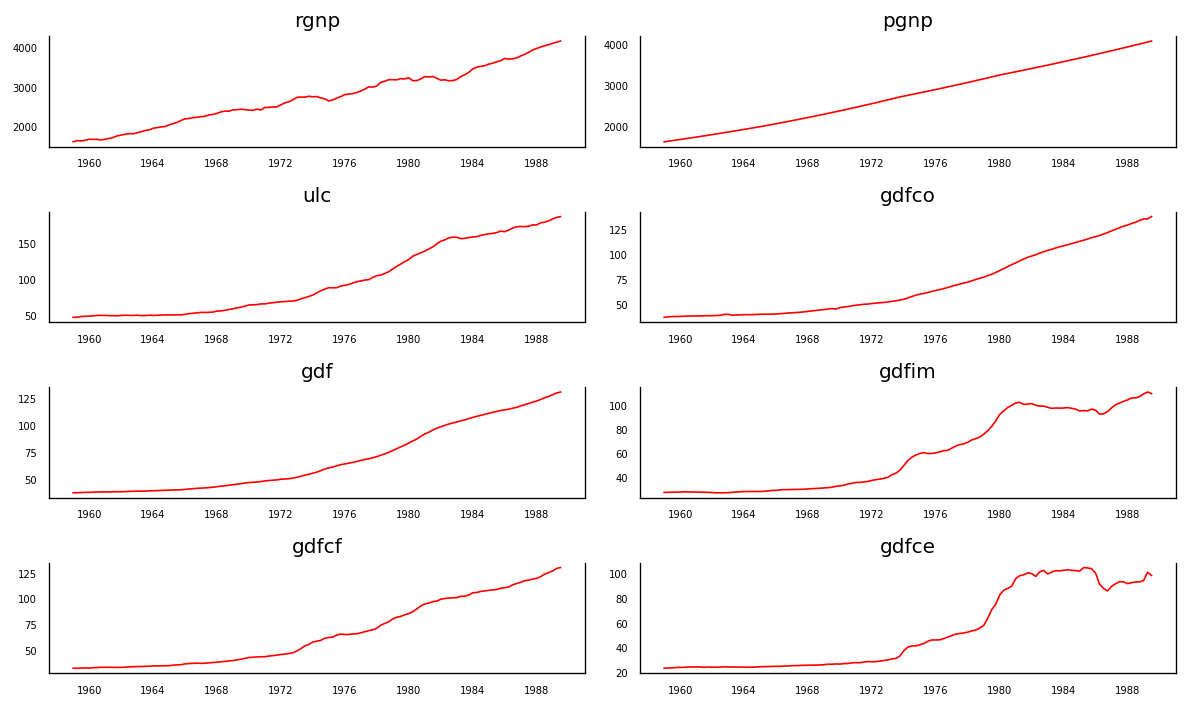
每个系列多年来都有相当相似的趋势模式,除了gdfim和gdfce,从 1980 年开始注意到不同的模式。
好的,分析的下一步是检查这些序列之间的因果关系。格兰杰因果关系检验和协整检验可以帮助我们解决这个问题。
3.4 使用格兰杰因果关系检验检验因果关系
矢量自动回归背后的基础是系统中的每个时间序列相互影响。也就是说,可以使用自身的过去值以及系统中的其他序列来预测序列。
使用格兰杰因果关系检验,甚至可以在构建模型之前测试这种关系。
格兰杰的因果关系到底检验的是什么呢?
格兰杰因果关系检验回归方程中过去值的系数为零的原假设。
简单来说,时间序列 (X) 的过去值不会导致其他序列 (Y)。因此,如果从检验获得的 p 值小于显著性水平 0.05,则可以安全地否定原假设。
下面的代码对给定数据帧中时间序列的所有可能组合实现格兰杰因果关系检验,并将每个组合的 p 值存储在输出矩阵中。
from statsmodels.tsa.stattools import grangercausalitytests
maxlag = 12
test = 'ssr_chi2test'
def grangers_causation_matrix(data, variables, test='ssr_chi2test', verbose=False): df = pd.DataFrame(np.zeros((len(variables), len(variables))), columns=variables, index=variables)for c in df.columns:for r in df.index:test_result = grangercausalitytests(data[[r, c]], maxlag=maxlag, verbose=False)p_values = [round(test_result[i+1][0][test][1],4) for i in range(maxlag)]if verbose: print(f'Y = {r}, X = {c}, P Values = {p_values}')min_p_value = np.min(p_values)df.loc[r, c] = min_p_valuedf.columns = [var + '_x' for var in variables]df.index = [var + '_y' for var in variables]return dfgrangers_causation_matrix(df, variables = df.columns)
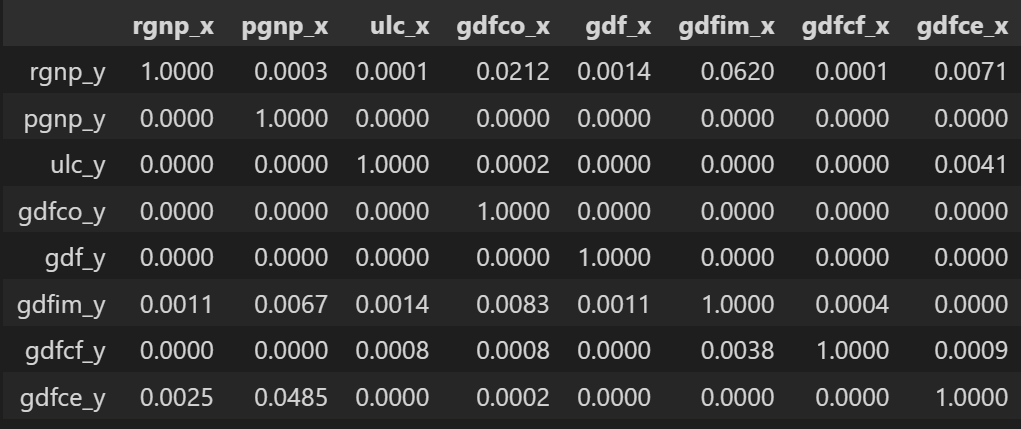
检查时间序列所有可能组合的格兰杰因果关系。行是响应变量,列是预测变量。
表中的值是 P 值。 P 值小于显着性水平 (0.05),意味着零假设对应的过去值的系数是零,即 X 不导致 Y 可以被拒绝。
Data: 包含时间序列变量的df数据框
variables : list containing names of the time series variables.
那么如何阅读上面的输出呢?行是响应 (Y),列是预测变量序列 (X)。
例如,如果在(第 0 行,第 0003 列)中取值 1.2,则它是指导致 的 p 值。而 0.000 in (第 2 行,第 1 列) 是指导致 的 p 值。pgnp_x rgnp_y rgnp_y pgnp_x
那么,如何解释p值呢?
如果给定的 p 值<显著性水平 (0.05),则相应的 X 系列(列)会导致 Y(行)。
例如,P 值 0.0003 在(第 1 行,第 2 列)表示原因的格兰杰因果关系检验的 p 值,该值小于显著性水平 0.05。pgnp_x rgnp_y
因此,我们可以拒绝原假设并得出结论原因。pgnp_x rgnp_y
查看上表中的 P 值,几乎可以观察到系统中的所有变量(时间序列)都是相互交替的。
这使得这种多时间序列系统成为使用 VAR 模型进行预测的良好候选者。
接下来,让我们进行协整测试。
3.5 协整测试
协整检验有助于确定两个或多个时间序列之间存在统计显著性联系。
但是,协整是什么意思?
要理解这一点,首先需要知道什么是“积分顺序”(d)。
积分阶数(d)只不过是使非平稳时间序列静止所需的差分数。
现在,当我们有两个或多个时间序列,并且存在它们的线性组合,其积分阶数 (d) 小于单个序列的阶数时,则序列集合称为共整。
还行?
当两个或多个时间序列共整时,这意味着它们具有长期的统计显著关系。
这是向量自回归(VAR)模型所基于的基本前提。因此,在开始构建VAR模型之前实施协整测试是相当普遍的。
好的,那么如何做这个测试呢?
参考论文:
https://www.jstor.org/stable/2938278?seq=1#page_scan_tab_contents
在Python中实现是相当简单的,如下所示:
from statsmodels.tsa.vector_ar.vecm import coint_johansendef cointegration_test(df, alpha=0.05): out = coint_johansen(df,-1,5)d = {'0.90':0, '0.95':1, '0.99':2}traces = out.lr1cvts = out.cvt[:, d[str(1 - alpha)]]def adjust(val, length = 6): return str(val).ljust(length)# Summaryprint('Name :: Test Stat > C(95%) => Signif \n', '--'*20)for col, trace, cvt in zip(df.columns, traces, cvts):print(adjust(col), ':: ', adjust(round(trace,2), 9), ">", adjust(cvt, 8), ' => ' , trace > cvt)cointegration_test(df)
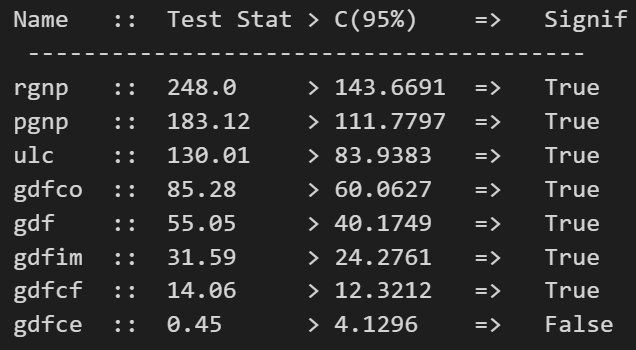
3.6 将序列拆分为训练数据和测试数据
将数据集拆分为训练数据和测试数据。
VAR模型将被拟合,然后用于预测接下来的4个观测值。这些预测将与测试数据中的实际值进行比较。
为了进行比较,我们将使用多个预测准确性指标,如本文后面所示。
nobs = 4
df_train, df_test = df[0:-nobs], df[-nobs:]# Check size
print(df_train.shape) # (119, 8)
print(df_test.shape) # (4, 8)
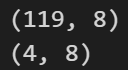
3.7 检查平稳性并使时间序列保持平稳
由于 VAR 模型要求要预测的时间序列是平稳的,因此习惯上检查系统中的所有时间序列的平稳性。
刷新一下,平稳时间序列是其特征(如均值和方差)不随时间变化的时间序列。
那么,如何测试平稳性呢?
有一套称为单位根测试的测试。流行的是:
- 增强迪基-富勒测试(ADF 测试)
- KPSS测试
- 菲利普-佩伦测试
让我们使用 ADF 测试来实现我们的目的。
顺便说一下,如果发现某个序列是非平稳的,则通过对序列进行一次差分并再次重复测试直到它变得平稳来使其平稳。
由于差分会将序列的长度减少 1,并且由于所有时间序列的长度必须相同,因此如果选择差分,则需要差分系统中的所有序列。
似乎明白了点
让我们实现 ADF 测试。
首先,我们实现一个不错的函数 (),它写出任何给定时间序列的 ADF 测试结果,并在每个序列上逐个实现此函数。adfuller_test()
def adfuller_test(series, signif=0.05, name='', verbose=False):"""Perform ADFuller to test for Stationarity of given series and print report"""r = adfuller(series, autolag='AIC')output = {'test_statistic':round(r[0], 4), 'pvalue':round(r[1], 4), 'n_lags':round(r[2], 4), 'n_obs':r[3]}p_value = output['pvalue'] def adjust(val, length= 6): return str(val).ljust(length)# Print Summaryprint(f' Augmented Dickey-Fuller Test on "{name}"', "\n ", '-'*47)print(f' Null Hypothesis: Data has unit root. Non-Stationary.')print(f' Significance Level = {signif}')print(f' Test Statistic = {output["test_statistic"]}')print(f' No. Lags Chosen = {output["n_lags"]}')for key,val in r[4].items():print(f' Critical value {adjust(key)} = {round(val, 3)}')if p_value <= signif:print(f" => P-Value = {p_value}. Rejecting Null Hypothesis.")print(f" => Series is Stationary.")else:print(f" => P-Value = {p_value}. Weak evidence to reject the Null Hypothesis.")print(f" => Series is Non-Stationary.")
在每个系列上调用:
# ADF Test on each column
for name, column in df_train.iteritems():adfuller_test(column, name=column.name)print('\n')
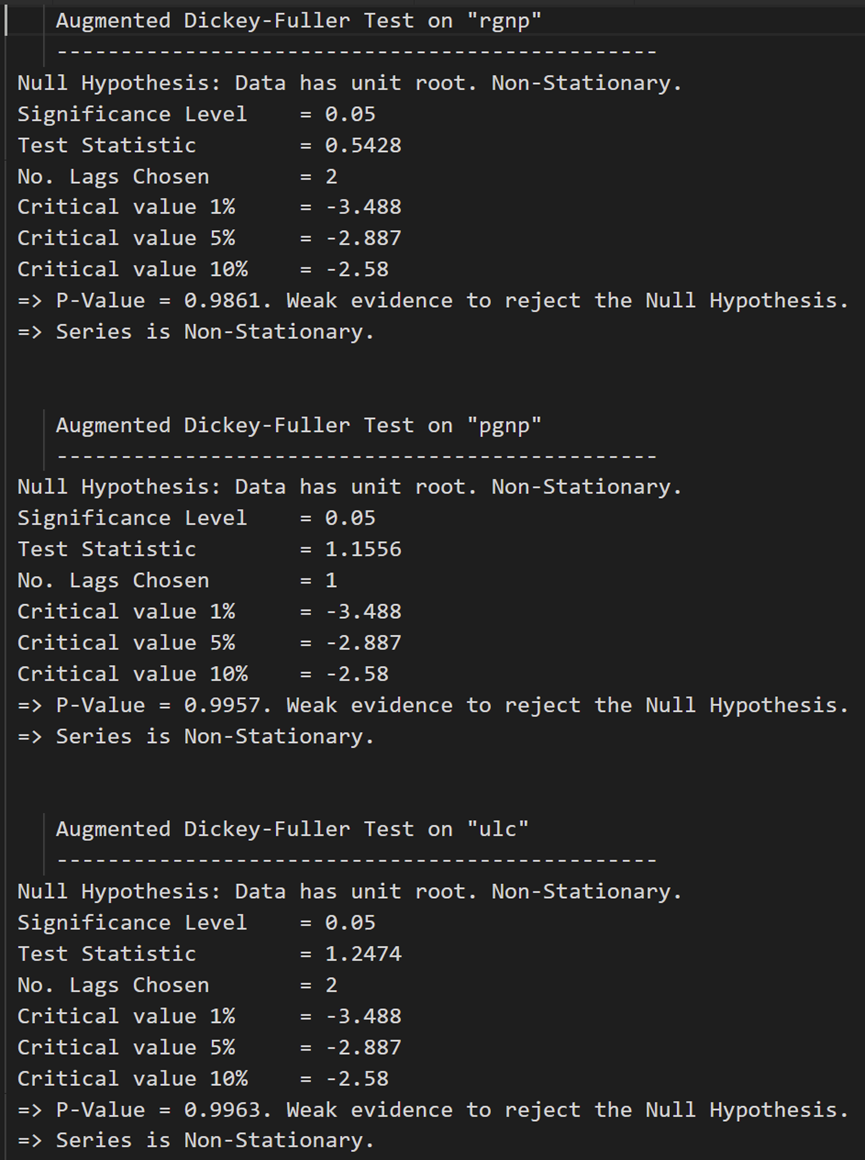
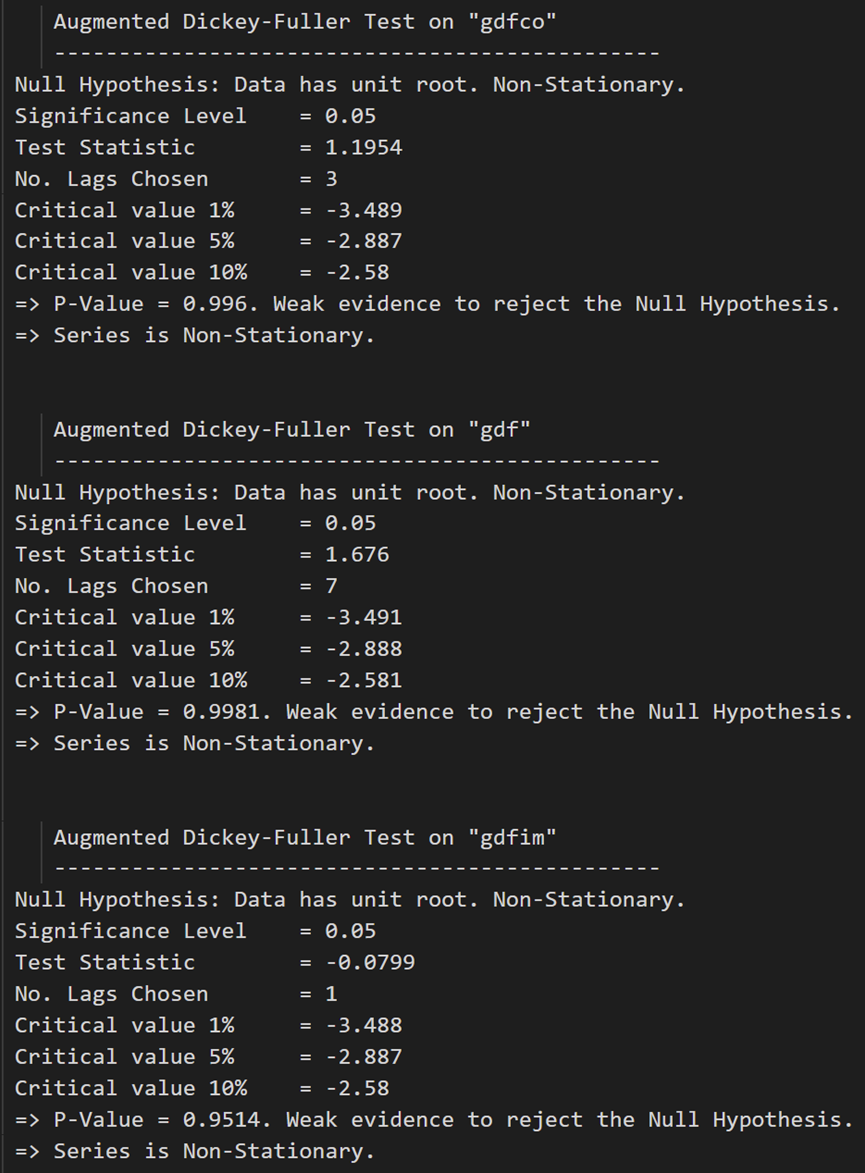
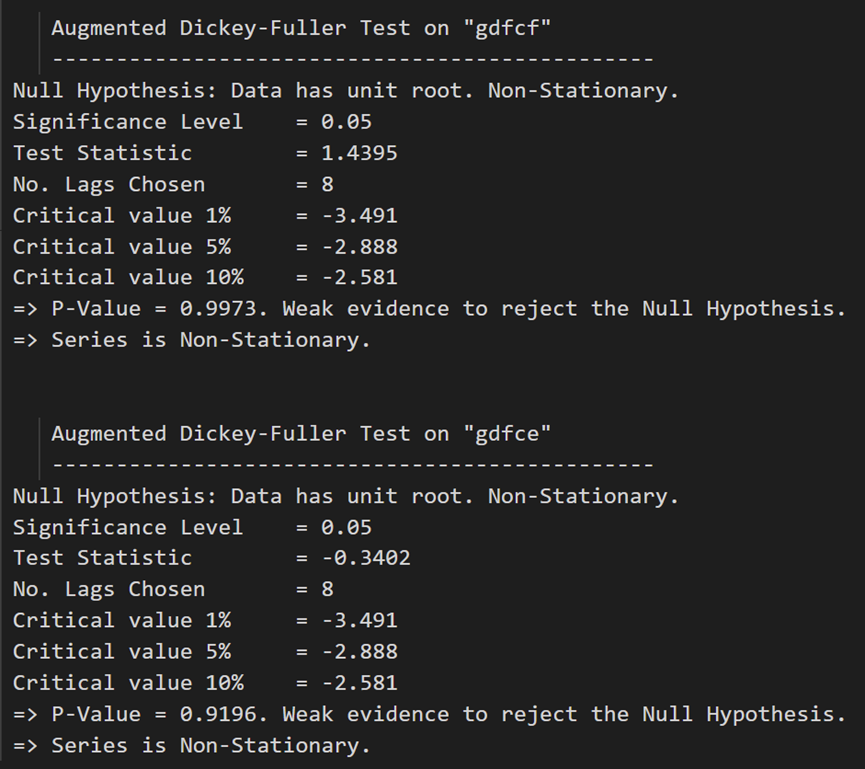
ADF 测试确认没有一个时间序列是静止的。让我们将它们全部差分一次,然后再次检查:
# 1st difference
df_differenced = df_train.diff().dropna()
# ADF Test on each column of 1st Differences Dataframe
for name, column in df_differenced.iteritems():adfuller_test(column, name=column.name)print('\n')
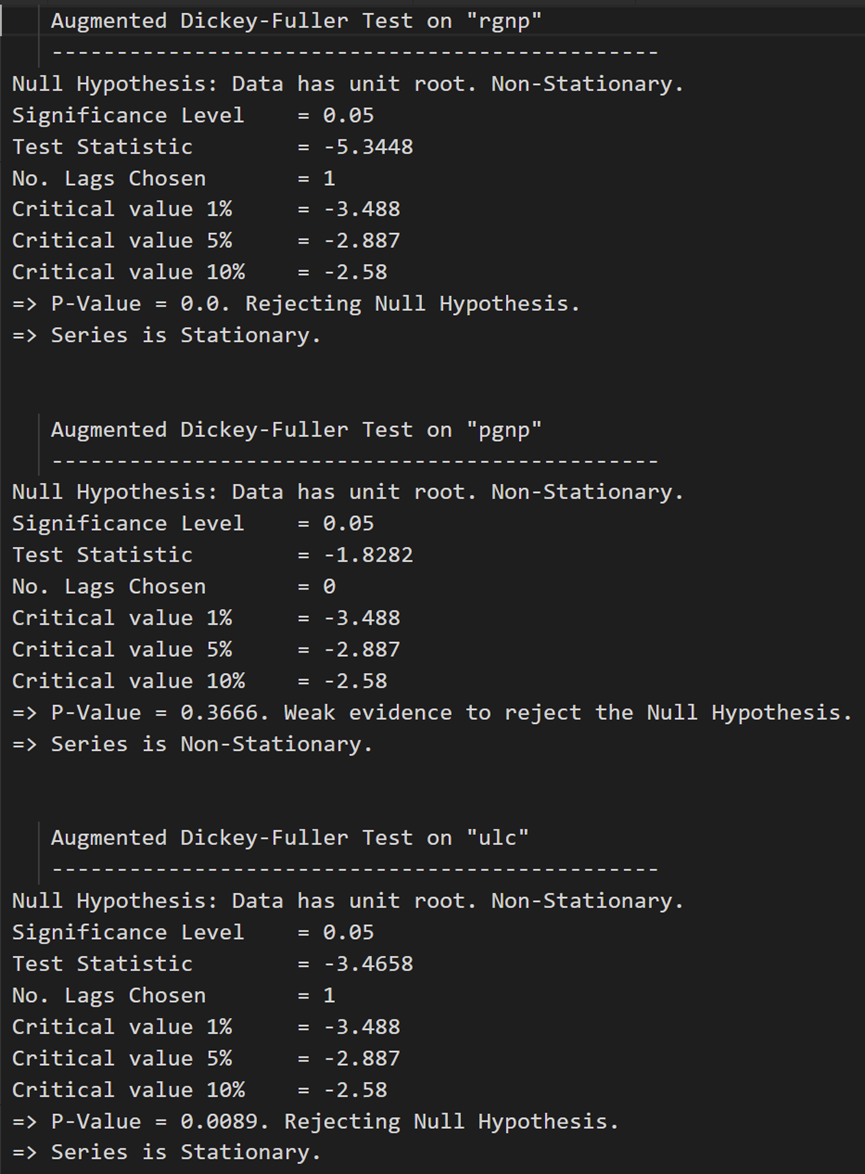
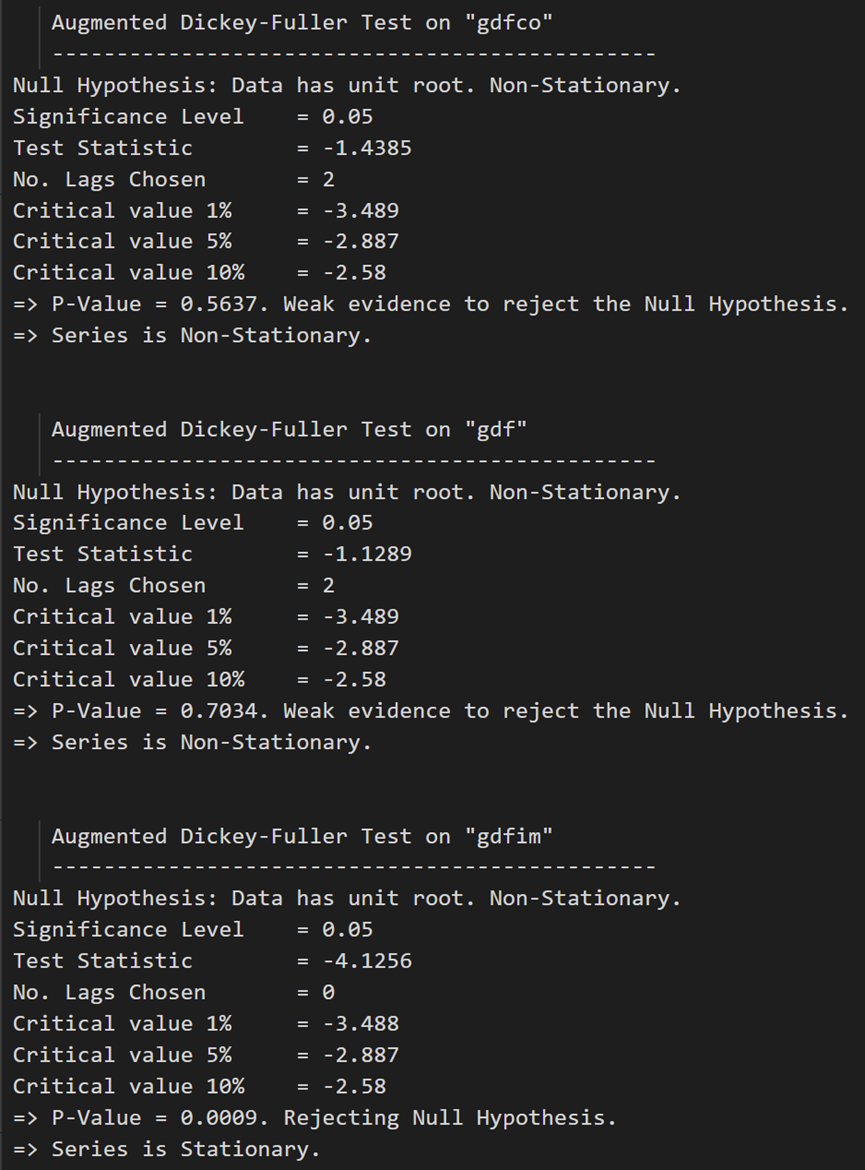
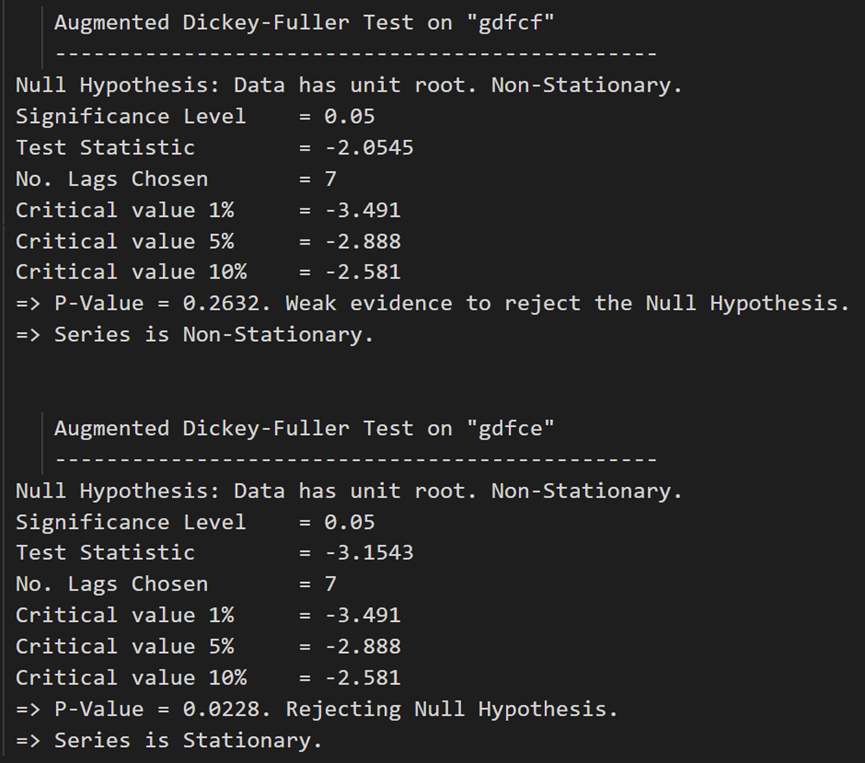
在第一个差分之后,实际工资(制造业)仍然不是静止的。它的临界值介于 5% 到 10% 的显著性水平之间。
VAR 模型中的所有序列都应具有相同数量的观测值。
因此,我们只剩下两个选择之一。
也就是说,要么继续第一个差分序列,要么再差一次所有系列。
# Second Differencing
df_differenced = df_differenced.diff().dropna()
再次运行 ADF 测试:
# ADF Test on each column of 2nd Differences Dataframe
for name, column in df_differenced.iteritems():adfuller_test(column, name=column.name)print('\n')
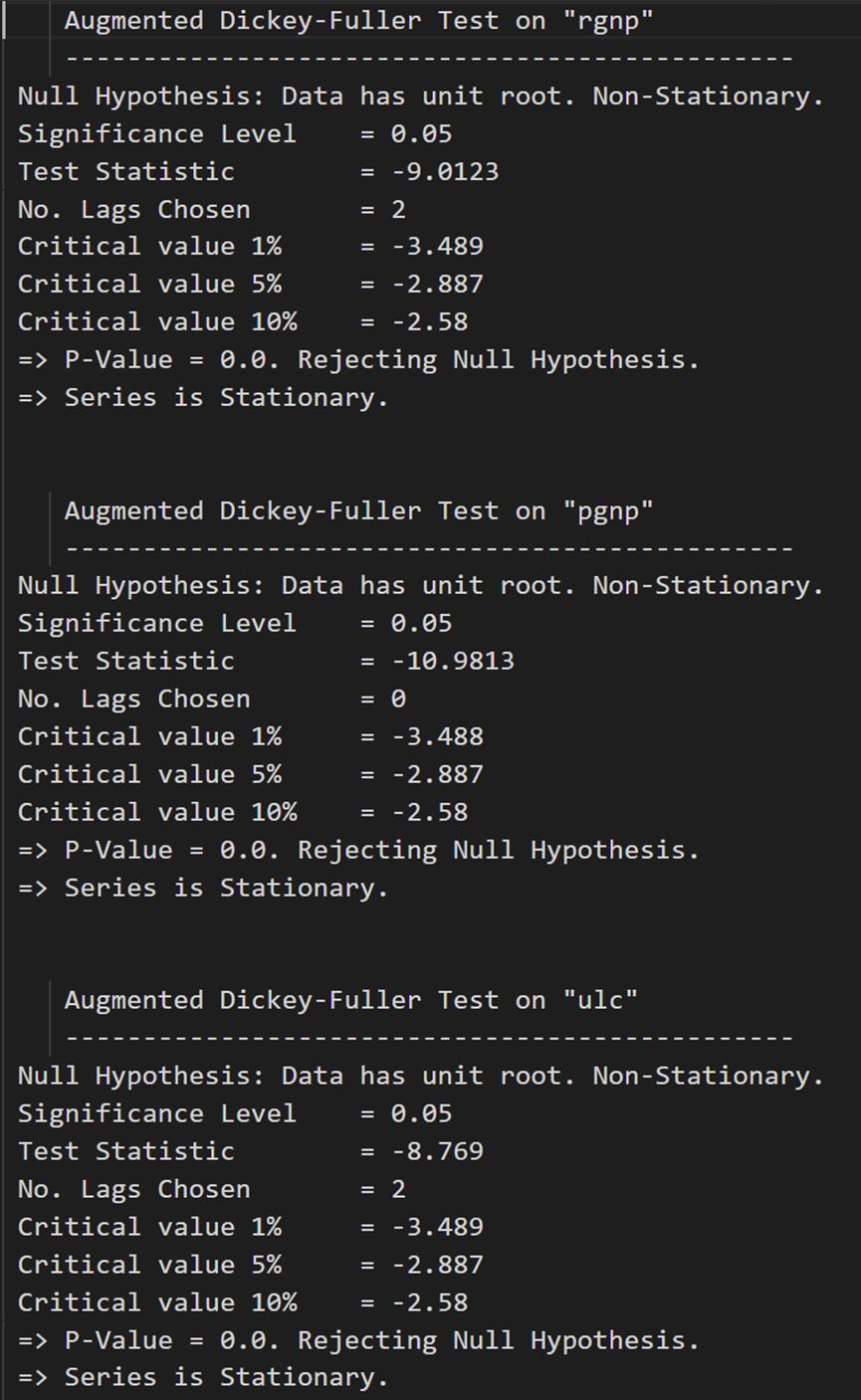
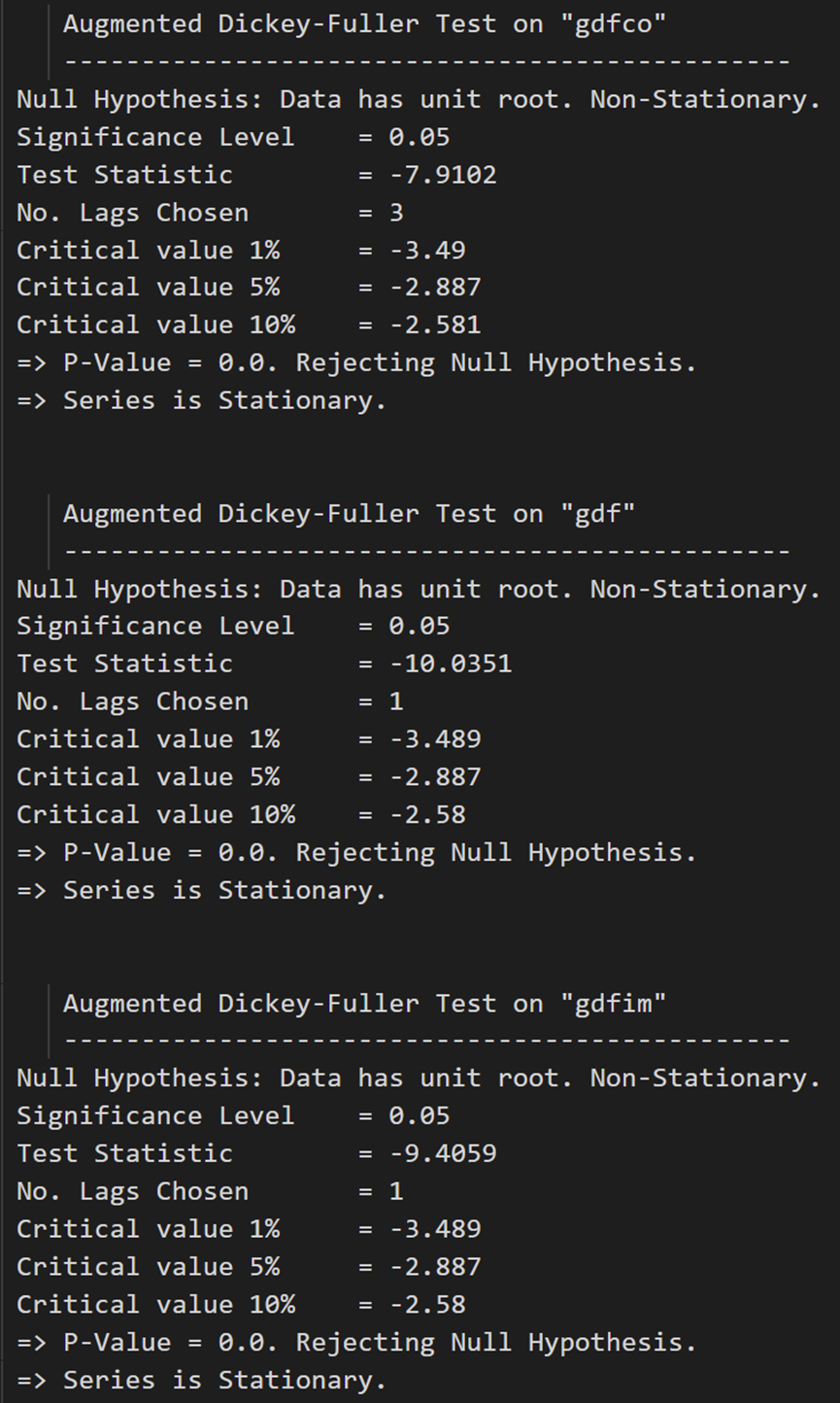
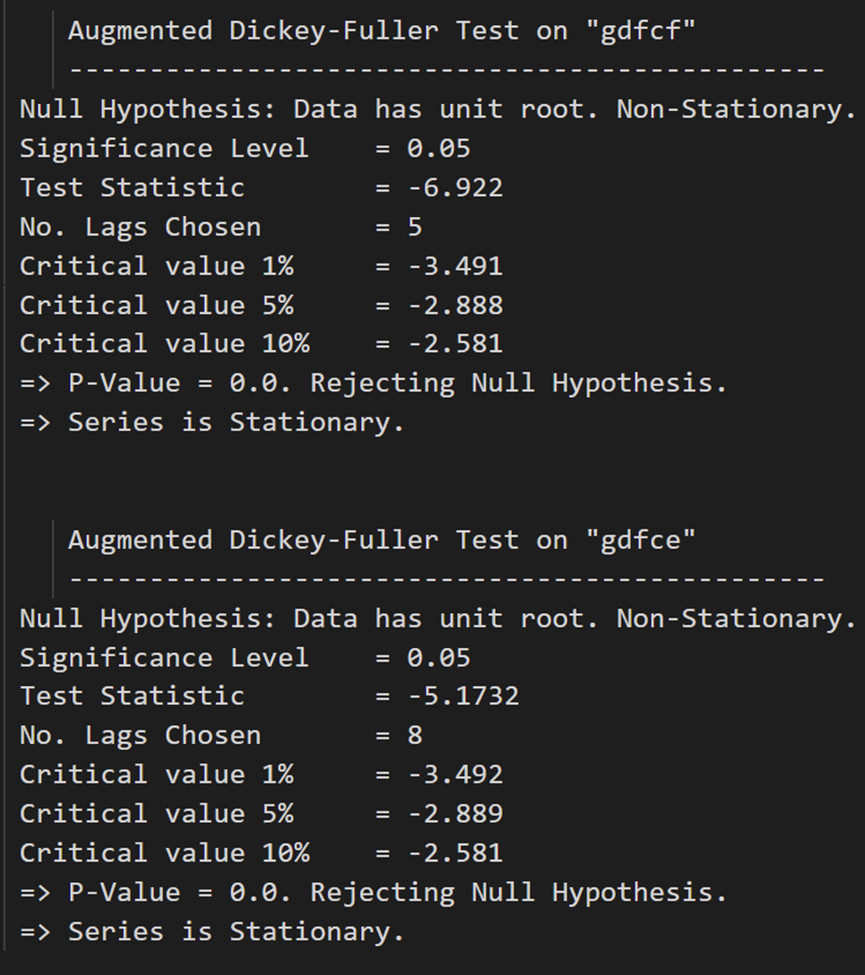
所有系列现在都是静止的。
让我们准备训练和测试数据集。
3.8 如何选择VAR模型的阶数(P)
为了选择 VAR 模型的正确顺序,我们迭代拟合 VAR 模型的递增阶数,并选择给出 AIC 最少模型的顺序。
虽然通常的做法是查看 AIC,但也可以检查BIC和FPE的其他最佳拟合比较估计值。
model = VAR(df_differenced)
for i in [1,2,3,4,5,6,7,8,9]:result = model.fit(i)print('Lag Order =', i)print('AIC : ', result.aic)print('BIC : ', result.bic)print('FPE : ', result.fpe)print('HQIC: ', result.hqic, '\n')
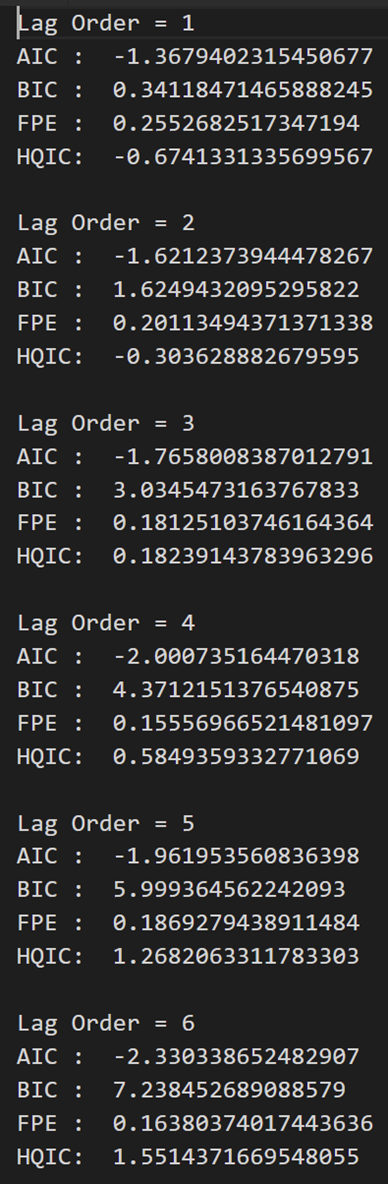
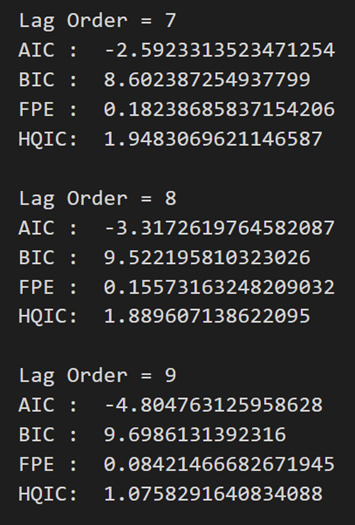
在上述输出中,AIC 在滞后 4 时降至最低,然后在滞后 5 处增加,然后持续进一步下降。
让我们使用滞后 4 模型。
选择 VAR 模型阶数 (p) 的另一种方法是使用该方法。model.select_order(maxlags)
所选顺序 (p) 是给出最低“AIC”、“BIC”、“FPE”和“HQIC”分数的顺序。
x = model.select_order(maxlags=12)
x.summary()
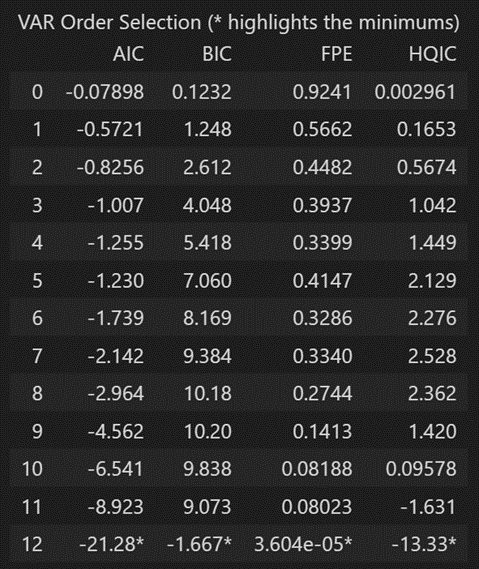
根据 FPE 和 HQIC,在 3 的滞后量级观察到最佳滞后。
但是,我没有解释为什么观察到的 AIC 和 BIC 值在使用时与在使用时看到的不同。
由于显式计算的 AIC 在滞后 4 时最低,因此我选择所选顺序为 4。
3.9 训练选定订单的VAR模型(p)
model_fitted = model.fit(4)
model_fitted.summary()
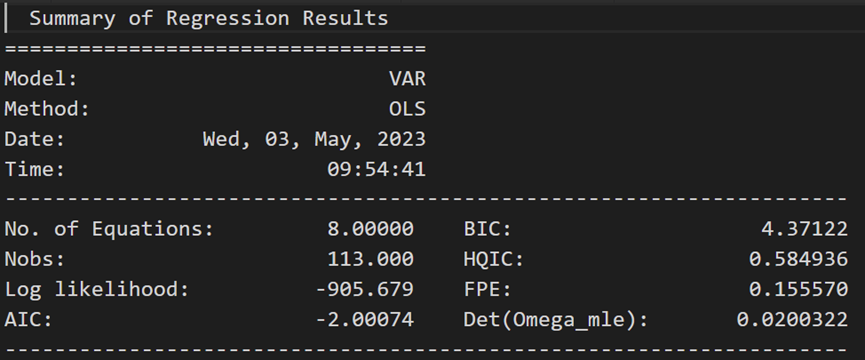
Results for equation rgnp:
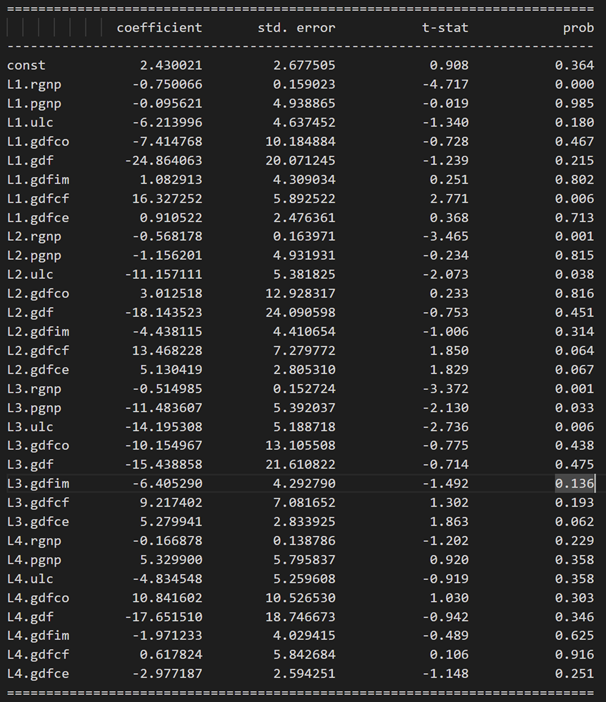
Results for equation pgnp:
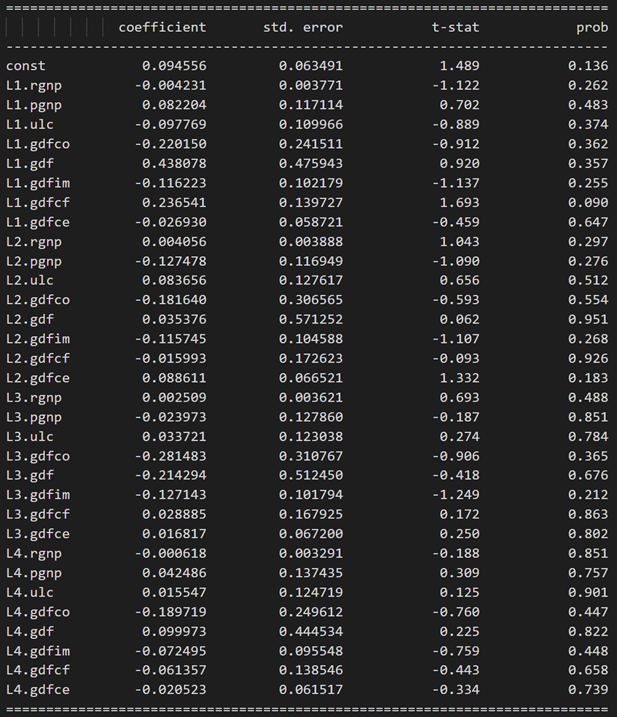
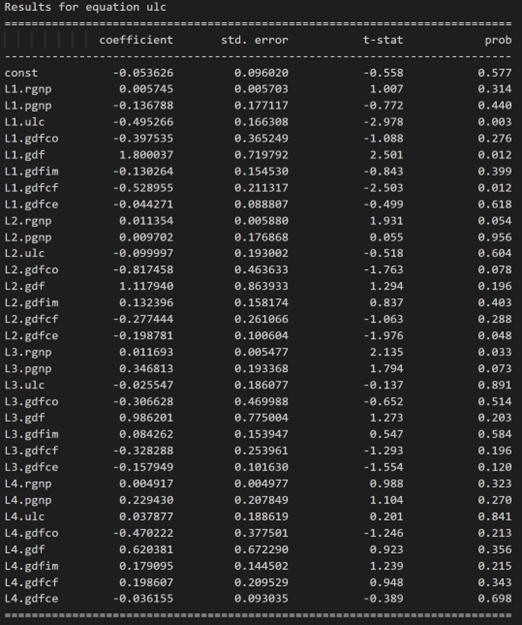
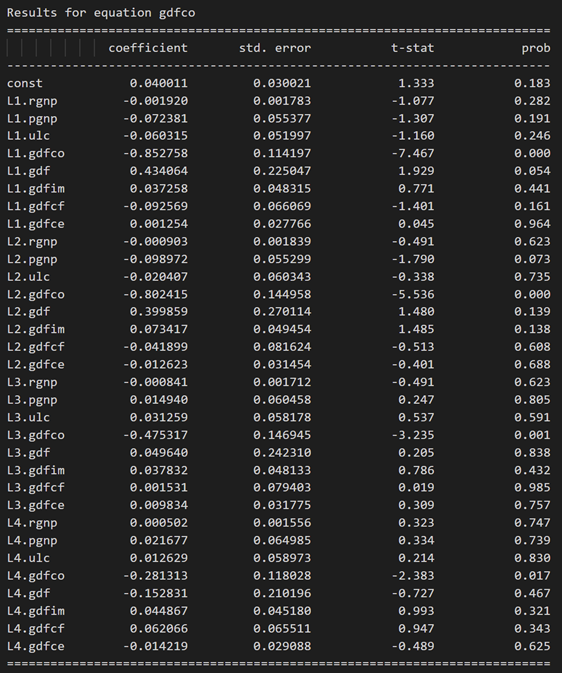
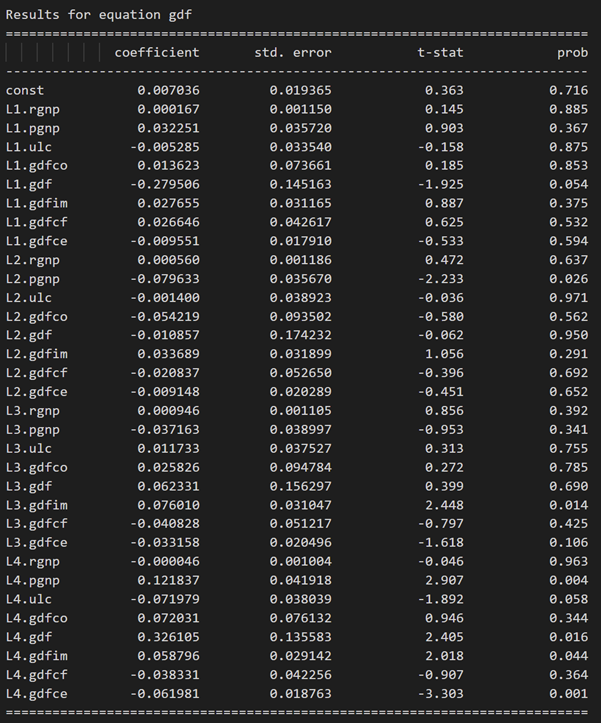
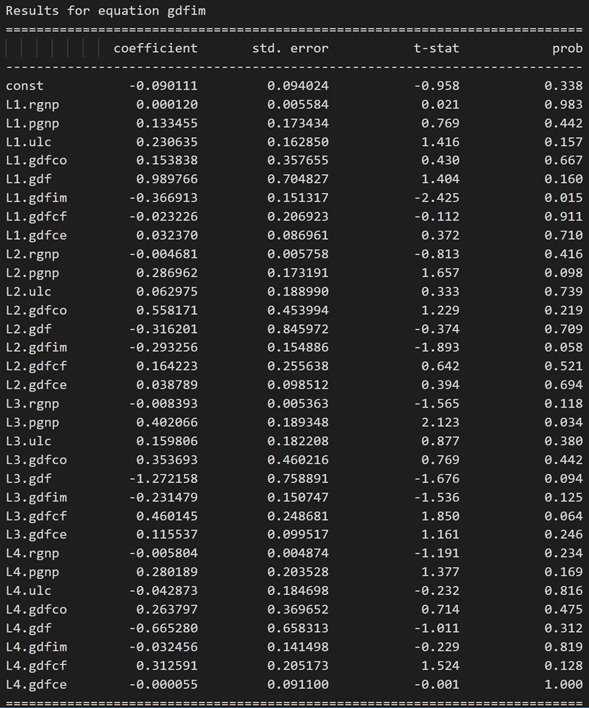
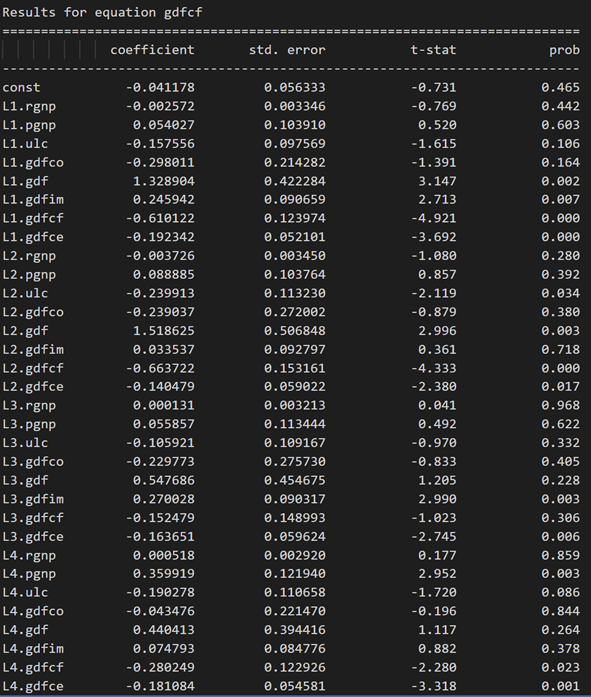
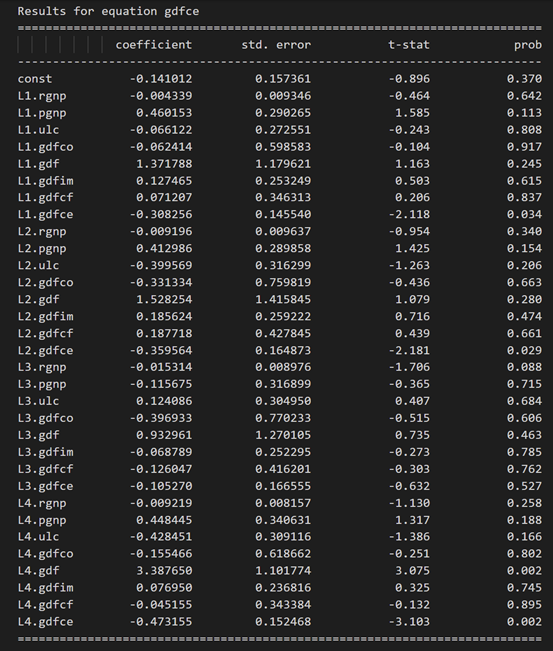
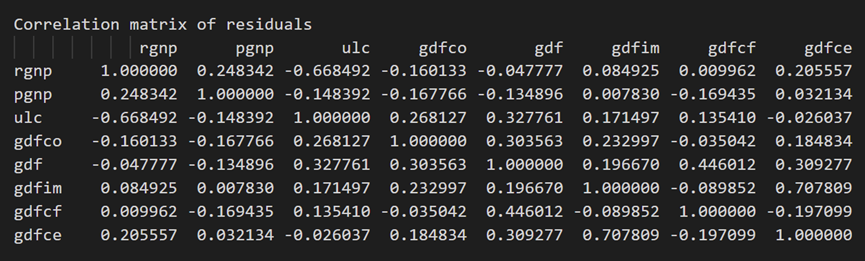
3.10 使用德宾沃森统计量检查残差(误差)的序列相关性
残差的序列相关性用于检查残差中是否存在任何剩余模式(误差)。
这对我们意味着什么?
如果残差中还存在任何相关性,那么时间序列中仍有一些模式有待模型解释。在这种情况下,典型的行动过程是增加模型的顺序或将更多预测因子引入系统,或者寻找不同的算法来对时间序列进行建模。
因此,检查序列相关性是为了确保模型能够充分解释时间序列中的方差和模式。
好了,回到正题。
检查误差序列相关性的常用方法是使用德宾沃森统计量进行测量。
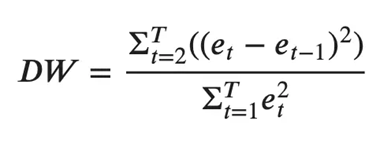
此统计数据的值可以在 0 到 4 之间变化。它越接近值 2,则没有显著的序列相关性。越接近 0,序列相关为正,越接近 4 表示序列相关为负。
from statsmodels.stats.stattools import durbin_watson
out = durbin_watson(model_fitted.resid)for col, val in zip(df.columns, out):print((col), ':', round(val, 2))
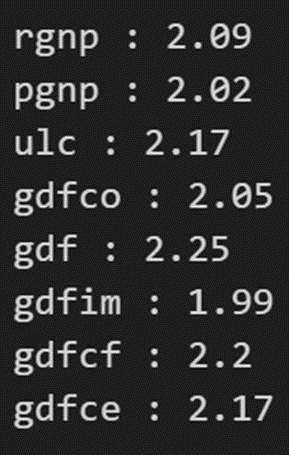
序列相关性似乎还不错。让我们继续进行预测。
3.11 如何使用统计模型预测VAR模型
为了进行预测,VAR 模型期望过去数据的观测值达到滞后顺序数。
这是因为,VAR 模型中的项本质上是数据集中各种时间序列的滞后,因此您需要为其提供模型使用的滞后顺序所指示的尽可能多的先前值。
# Get the lag order
lag_order = model_fitted.k_ar
print(lag_order) #> 4# Input data for forecasting
forecast_input = df_differenced.values[-lag_order:]
forecast_input

让我们预测一下:
# Forecast
fc = model_fitted.forecast(y=forecast_input, steps=nobs)
df_forecast = pd.DataFrame(fc, index=df.index[-nobs:], columns=df.columns + '_2d')
df_forecast
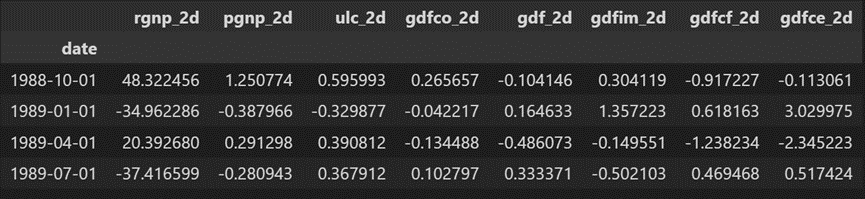
预测是生成的,但它是模型使用的训练数据的规模。因此,要使其恢复到原始比例,您需要将其去差分,就像对原始输入数据进行差分的次数一样。
在这种情况下,它是两次。
3.12 反转变换以获得真实预测
def invert_transformation(df_train, df_forecast, second_diff=False):df_fc = df_forecast.copy()columns = df_train.columnsfor col in columns: # Roll back 2nd Diffif second_diff:df_fc[str(col)+'_1d'] = (df_train[col].iloc[-1]-df_train[col].iloc[-2]) + df_fc[str(col)+'_2d'].cumsum()# Roll back 1st Diffdf_fc[str(col)+'_forecast'] = df_train[col].iloc[-1] + df_fc[str(col)+'_1d'].cumsum()return df_fc
df_results = invert_transformation(df_train, df_forecast, second_diff=True)
df_results.loc[:, ['rgnp_forecast', 'pgnp_forecast', 'ulc_forecast', 'gdfco_forecast','gdf_forecast', 'gdfim_forecast', 'gdfcf_forecast', 'gdfce_forecast']]

预测恢复到原来的规模。让我们根据测试数据的实际值绘制预测值。
3.13 预测与实际图
fig, axes = plt.subplots(nrows=int(len(df.columns)/2), ncols=2, dpi=150, figsize=(10,10))
for i, (col,ax) in enumerate(zip(df.columns, axes.flatten())):df_results[col+'_forecast'].plot(legend=True, ax=ax).autoscale(axis='x',tight=True)df_test[col][-nobs:].plot(legend=True, ax=ax);ax.set_title(col + ": Forecast vs Actuals")ax.xaxis.set_ticks_position('none')ax.yaxis.set_ticks_position('none')ax.spines["top"].set_alpha(0)ax.tick_params(labelsize=6)plt.tight_layout()
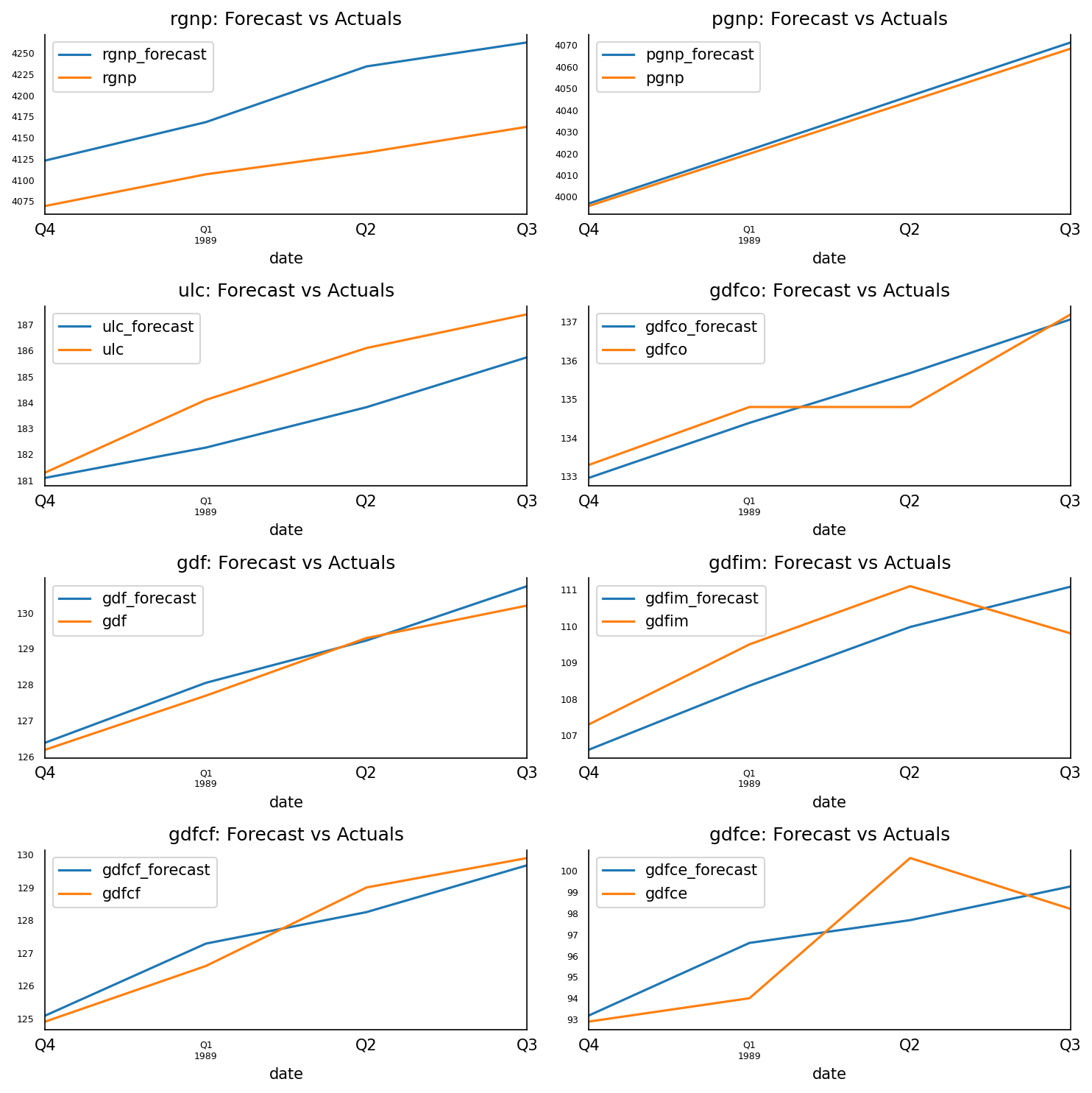
3.14 评估预测
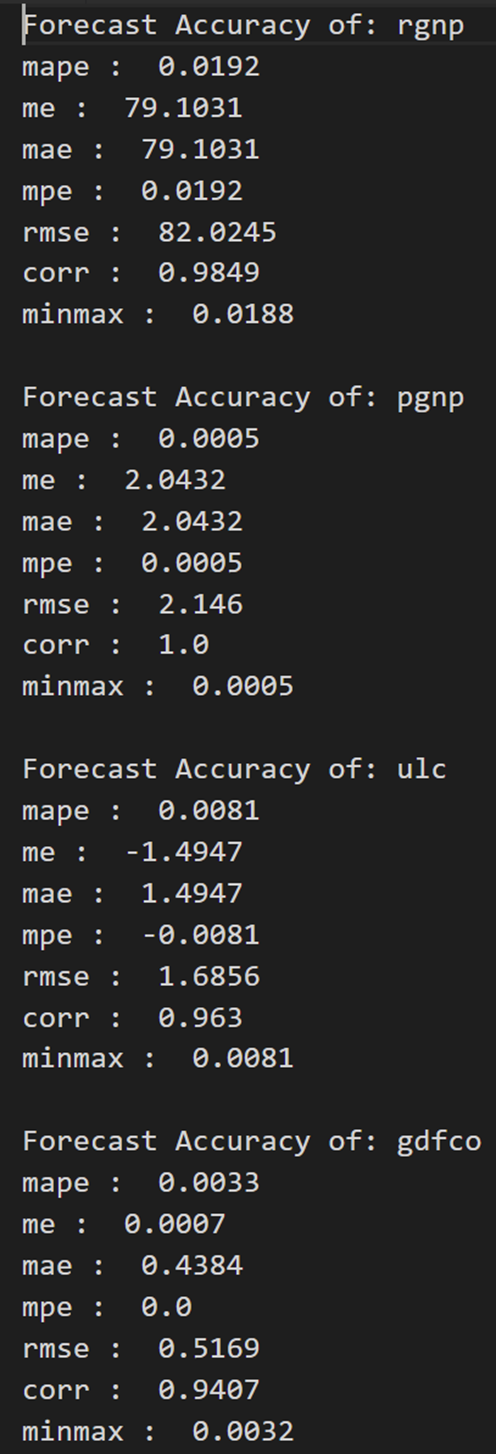
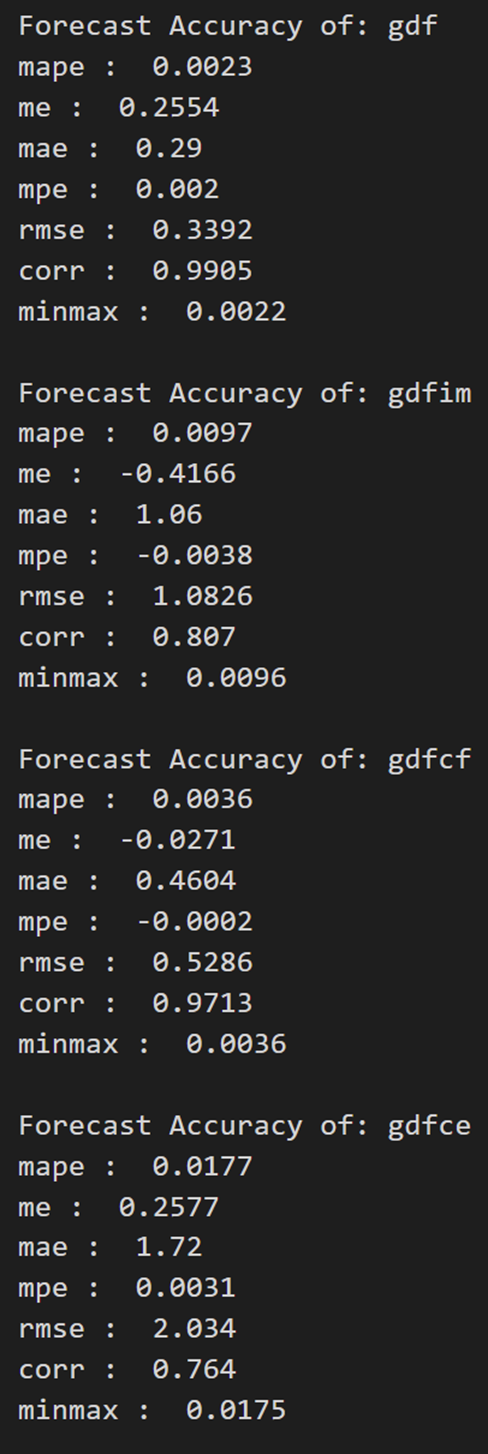
为了评估预测,让我们计算一组全面的指标,即MAPE,ME,MAE,MPE,RMSE,corr和minmax。
from statsmodels.tsa.stattools import acf
def forecast_accuracy(forecast, actual):mape = np.mean(np.abs(forecast - actual)/np.abs(actual)) # MAPEme = np.mean(forecast - actual) # MEmae = np.mean(np.abs(forecast - actual)) # MAEmpe = np.mean((forecast - actual)/actual) # MPErmse = np.mean((forecast - actual)**2)**.5 # RMSEcorr = np.corrcoef(forecast, actual)[0,1] # corrmins = np.amin(np.hstack([forecast[:,None], actual[:,None]]), axis=1)maxs = np.amax(np.hstack([forecast[:,None], actual[:,None]]), axis=1)minmax = 1 - np.mean(mins/maxs) # minmaxreturn({'mape':mape, 'me':me, 'mae': mae, 'mpe': mpe, 'rmse':rmse, 'corr':corr, 'minmax':minmax})print('Forecast Accuracy of: rgnp')
accuracy_prod = forecast_accuracy(df_results['rgnp_forecast'].values, df_test['rgnp'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: pgnp')
accuracy_prod = forecast_accuracy(df_results['pgnp_forecast'].values, df_test['pgnp'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: ulc')
accuracy_prod = forecast_accuracy(df_results['ulc_forecast'].values, df_test['ulc'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: gdfco')
accuracy_prod = forecast_accuracy(df_results['gdfco_forecast'].values, df_test['gdfco'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: gdf')
accuracy_prod = forecast_accuracy(df_results['gdf_forecast'].values, df_test['gdf'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: gdfim')
accuracy_prod = forecast_accuracy(df_results['gdfim_forecast'].values, df_test['gdfim'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: gdfcf')
accuracy_prod = forecast_accuracy(df_results['gdfcf_forecast'].values, df_test['gdfcf'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))print('\nForecast Accuracy of: gdfce')
accuracy_prod = forecast_accuracy(df_results['gdfce_forecast'].values, df_test['gdfce'])
for k, v in accuracy_prod.items():print(k, ': ', round(v,4))
相关文章:

【VAR模型 | 时间序列】帮助文档:VAR模型的引入和Python实践(含源代码)
向量自回归 (VAR) 是一种随机过程模型,用于捕获多个时间序列之间的线性相互依赖性。 VAR 模型通过允许多个进化变量来概括单变量自回归模型(AR 模型)。 VAR 中的所有变量都以相同的方式进入模型:每个变量都有一个方程式ÿ…...
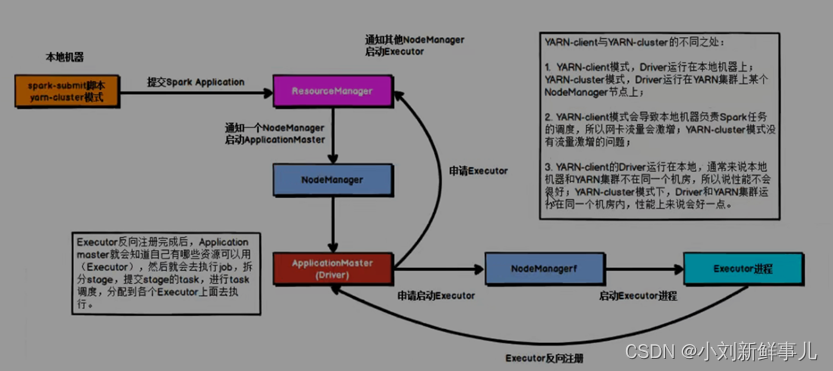
Spark任务提交流程
1. yarn-client Driver在任务提交的本地机器上运行,Driver启动后会和ResourceManager通讯,申请启动ApplicationMaster; 随后ResourceManager分配Container,在合适的NodeManager上启动ApplicationMaster,此时的ApplicationMaster的…...
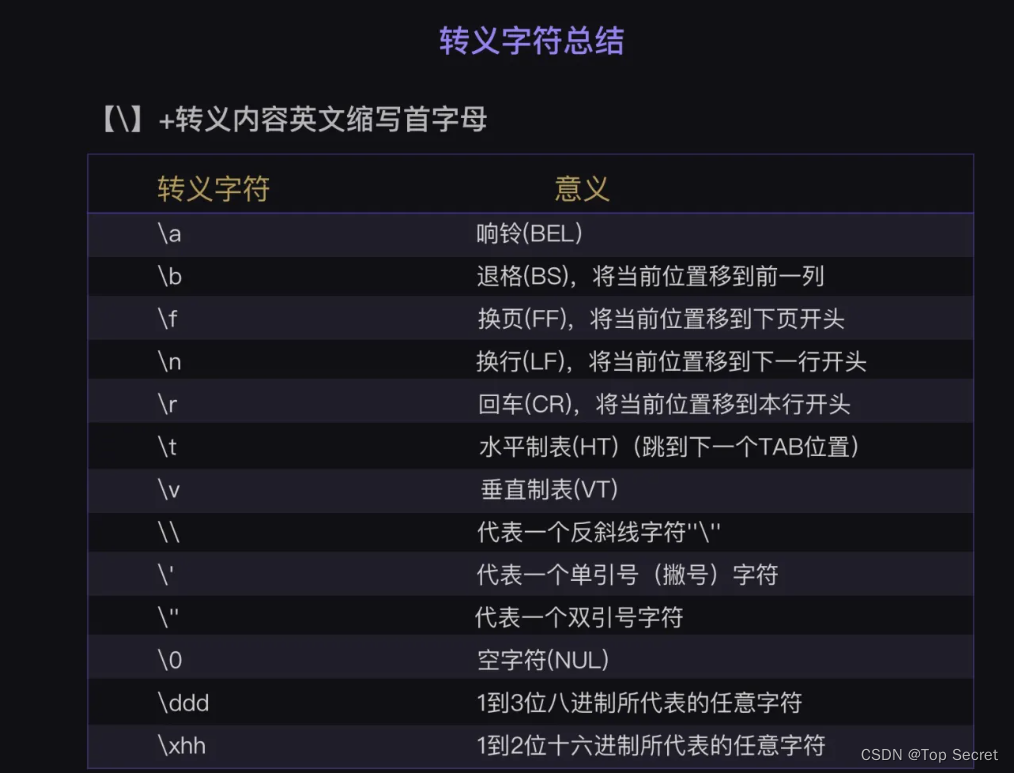
python相对路径与绝对路径
9.1 Python 绝对路径与相对路径 - 知乎 (zhihu.com) 目录 1. 绝对路径 1.1 概念 1.2 用绝对路径打开文件 1.2 相对路径 1.3 python路径表示的斜杠问题 1. 绝对路径 1.1 概念 绝对路径 指完整的描述文件位置的路径。绝对路径就是文件或文件夹在硬盘上的完整路径。 在 Win…...
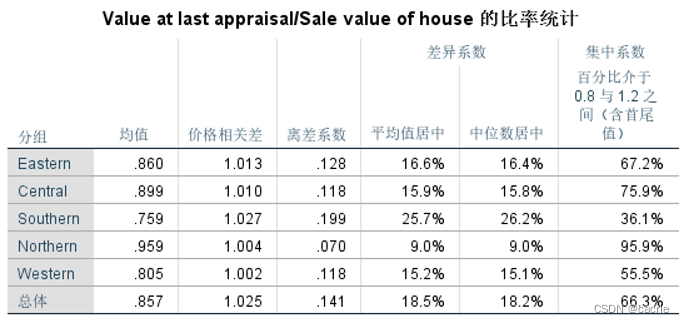
SPSS如何进行基本统计分析之案例实训?
文章目录 0.引言1.描述性分析2.频数分析3.探索分析4.列联表分析5.比率分析 0.引言 因科研等多场景需要进行数据统计分析,笔者对SPSS进行了学习,本文通过《SPSS统计分析从入门到精通》及其配套素材结合网上相关资料进行学习笔记总结,本文对基本…...
)
Python项目实战篇——常用验证码标注和识别(需求分析和实现思路)
前言:验证码识别和标注是现在网络安全中的一个重要任务,尤其是在一些电商平台和在线支付等场景中,验证码的安全性至关重要。本文将介绍如何使用Python实现常用的验证码标注和识别,以便为自己的项目提供参考。 一、需求分析 1、验证…...
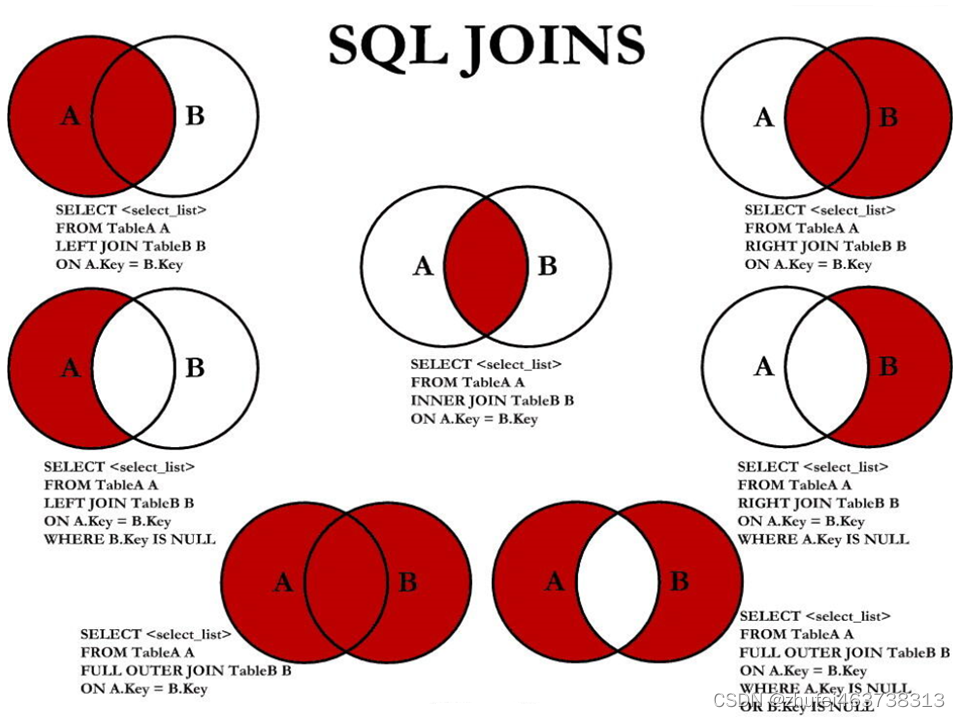
MySQL基础(六)多表查询
多表查询,也称为关联查询,指两个或更多个表一起完成查询操作。 前提条件:这些一起查询的表之间是有关系的(一对一、一对多),它们之间一定是有关联字段,这个关联字段可能建立了外键,…...
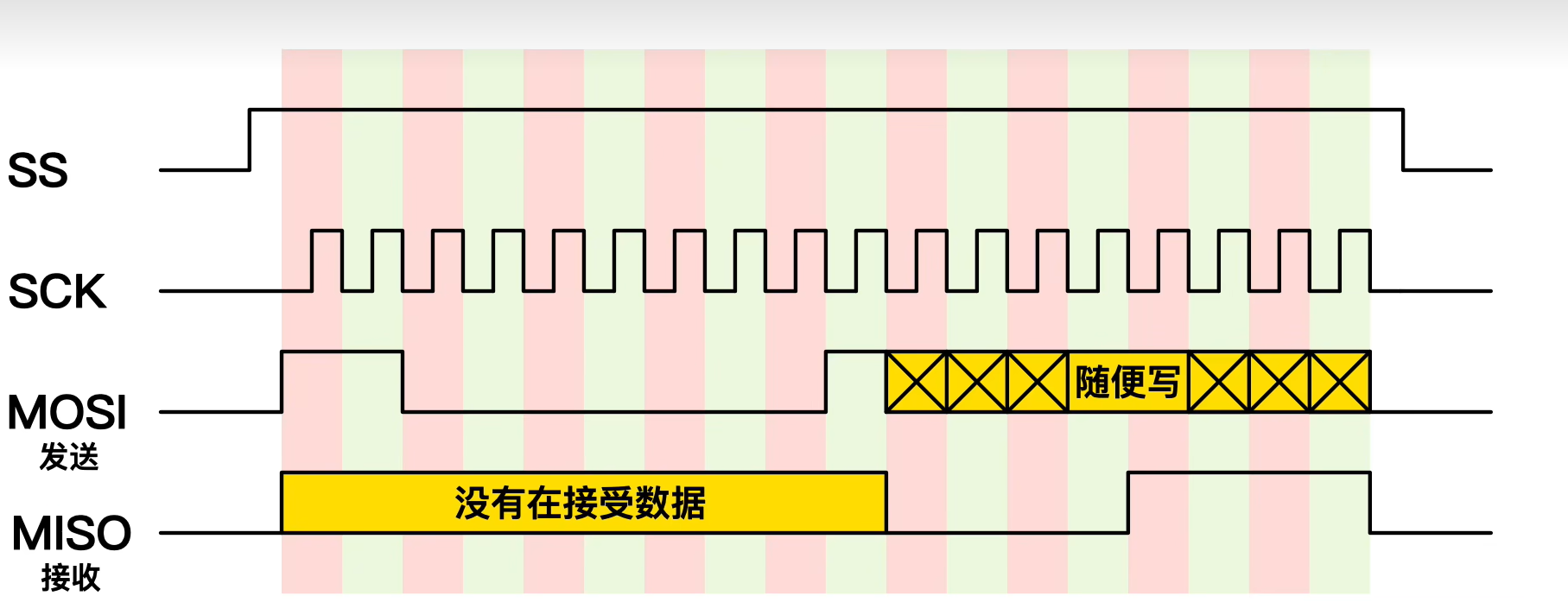
零死角玩转stm32中级篇3-SPI总线
本篇博文目录: 一.基础知识1.什么是SPI2.SPI和IIC有什么不同3.SPI的优缺点4.SPI是怎么实现通信的5.SPI 数据传输的步骤6.SPI菊花链7.通过SPI实现数据的读和写 二.STM32F103C8T6芯片SPI协议案例代码 一.基础知识 1.什么是SPI SPI(Serial Peripheral Interface&#…...
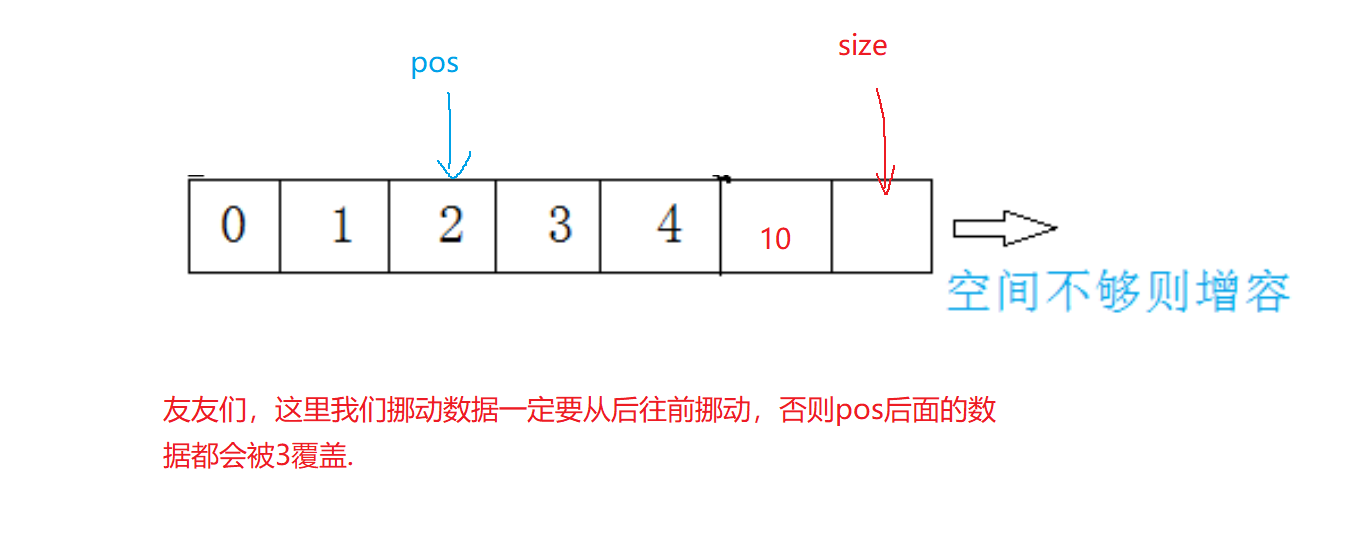
顺序表功能实现(入手版详解)
🍉博客主页:阿博历练记 📖文章专栏:数据结构与算法 🚚代码仓库:阿博编程日记 🌹欢迎关注:欢迎友友们点赞收藏关注哦 文章目录 🍓前言✨顺序表🔍1.顺序表的整体…...
)
Java 中的线程是什么,如何创建和管理线程-下(十三)
书接上文 CompletableFuture CompletableFuture 是 Java 8 中新增的类,提供了更为强大的异步编程支持。它可以将多个异步任务组合成一个整体,并且可以处理异常情况。 例如,可以使用 CompletableFuture 来实现异步任务的串行执行࿱…...

为什么我的Windows 10 便签不支持更改字体?
Windows便签是一款常用的记录工具,可以帮助我们快速记录一些重要的信息。在使用Windows便签时,如果你想要更好地呈现你的信息,可以通过设置字体来达到这个效果。本文将介绍Windows便签字体设置的相关知识,希望对你有所帮助。 1、打…...
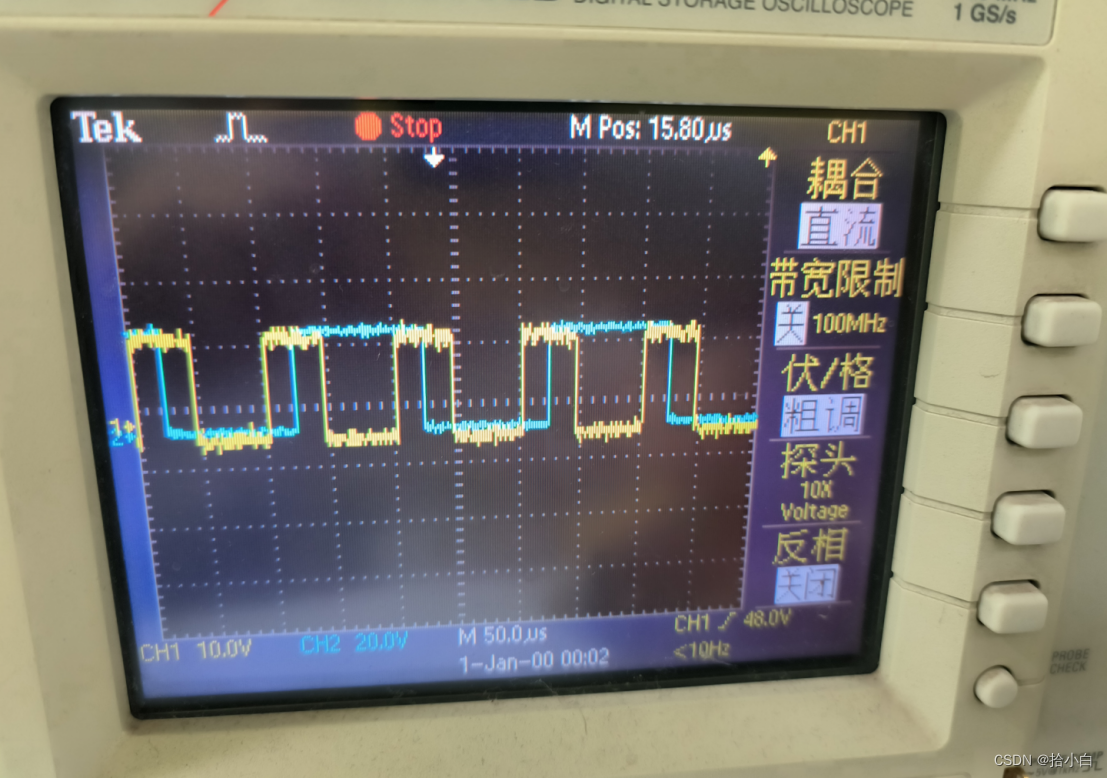
野火STM32电机系列(六)Cubemx配置ADC规则和注入通道
前文已经配置了GPIO、编码器 本节讲解CubeMXADC规则和注入通道 本文adc注入通道采用定时器触发,因此在上文定时器配置的基础上进行 常规信号(温度等)使用带DMA的常规通道连续采样 注入采样由定时器触发,采集电机三相电流&…...

预制菜,巨头们的新赛场
俗话说“民以食为天”,饮食对于大众的重要性自然是无需赘述。然而,随着生活节奏的加快,越来越多年轻人没有时间和精力去烹制菜肴,这也是外卖行业持续火热的重要原因之一。尽管如此,随着消费者健康意识的持续提升&#…...

英语语法第一章之英语语法综述
英语的任何句型基本都可以翻译成 什么怎么样 ,在这里什么就是我们常说的主语,而怎么样就是我们常说的谓语; 可能有些小伙伴会反问,不是主谓宾吗?别急等我慢慢讲解 在这里谓语也有很有多的不同的动作 可以独立完成的动作 句型&am…...
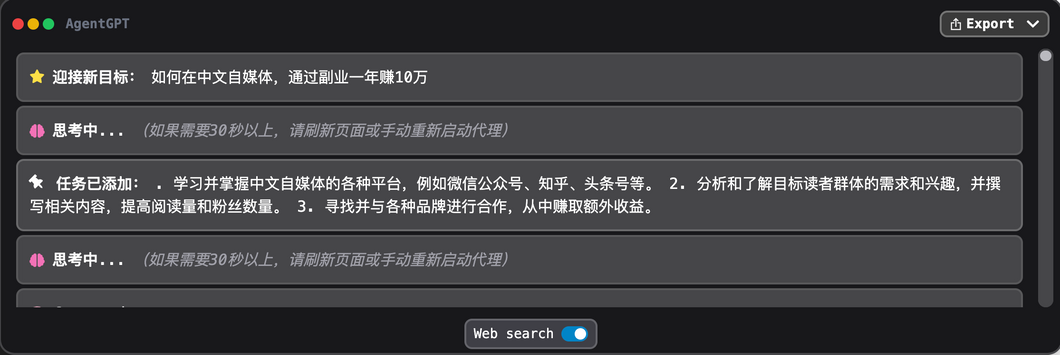
ChatGPT被淘汰了?Auto-GPT到底有多强
大家好,我是可夫小子,关注AIGC、读书和自媒体。解锁更多ChatGPT、AI绘画玩法。 说Auto-GPT淘汰了ChatGPT了,显然是营销文案里面的标题党。毕竟它还是基于ChatGPT的API,某种意义只是基于ChatGPT能力的应用。但最近,Auto…...
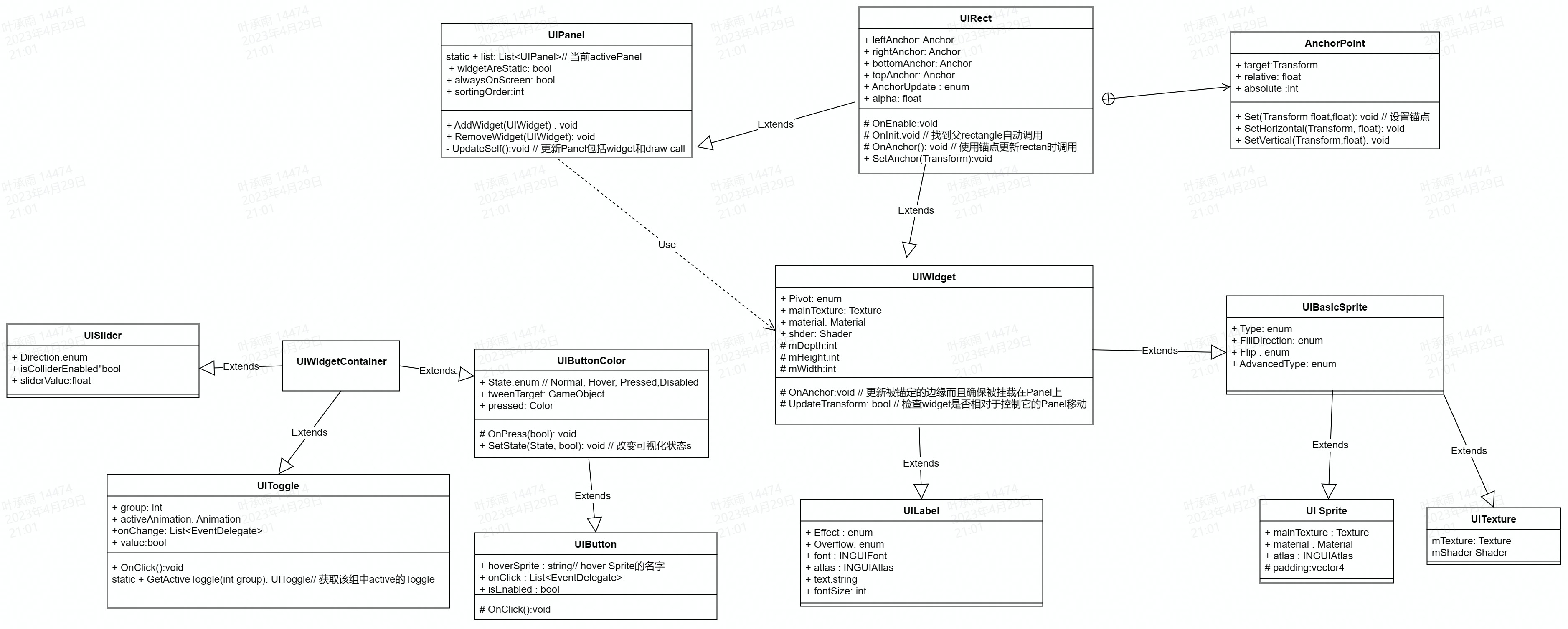
unity NGUI使用方法
基本用法 很多基本模块比如按钮、slider等都能从Prefab中直接拖拽到场景中实现,但都需要有一个Collider(Prefab已经自带) 因为不仅是UI,所有带有Collider的游戏物体都能接收到OnClick, OnPress这样的事件——前提是需…...
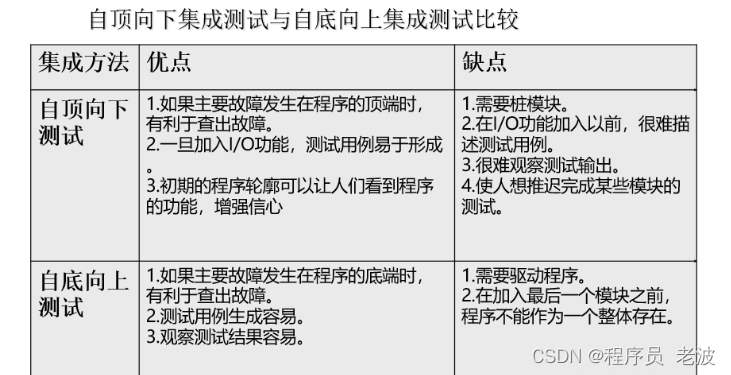
软件测试技术(五)软件测试流程
软件测试流程 软件测试流程如下: 测试计划测试设计测试执行 单元测试集成测试确认测试系统测试验收测试回归测试验证活动 测试计划 测试计划由测试负责人来编写,用于确定各个测试阶段的目标和策略。这个过程将输出测试计划,明确要完成的测…...

Redis缓存穿透和雪崩
Redis缓存穿透和雪崩 Redis缓存的使用,极大的提升了应用程序的性能和效率,特别是数据查询方面。但同时,它也带来了一些问题。其中,最要害的问题,就是数据的一致性问题,从严格意义上讲,这个问题…...

【C++】set和map的使用
对于STL容器来说,有很多相似的功能,所以这里主要将与之前不同的功能说清楚 文章目录 1.对于set与map的简单理解2. setinsert迭代器遍历countmultisetinsertfindcount 3. mapinsert与迭代器的使用统计水果次数 operator []operator[]的实现理解对整体的拆…...

大学生学java编程的就业前景怎么样?我来聊聊自己的见解
今天兴哥想跟大家分享一个话题,就是学java到底好不好找工作。因为我发现很多粉丝朋友,之前可能并不是从事IT行业的,然后想转行来做这一行,或者是有些大四即将面临毕业的老哥,可能大学没有好好学习吧,然后专…...
JavaScript全解析——canvas 入门(上)
●canvas 是 HTML5 新增的一个标签, 表示画布 ●canvas 也是 h5 的画布技术, 我们通过代码的方式在画布上描绘一个图像 canvas 标签 ●向进行 canvas 绘图, 首先我们先要了解到 canvas 标签 ●是 html5 推出的一个标签 <html> <head>... </head> <body&…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
