数据库设计-范式
范式
范式就是数据库的构建规则,目前关系数据库有六种范式:第一范式(1NF)、第二范式(2NF)、第三范式(3NF)、第四范式(4NF)、第五范式(5NF)和第六范式(6NF)。满足最低要求的范式是第一范式(1NF)。在第一范式的基础上进一步满足更多要求的称为第二范式(2NF),其余范式以次类推。一般说来,数据库只需满足第三范式(3NF)就行了。
1NF(第一范式)
特征:无重复列
官方解释:在关系模式R中的每一个具体关系r中,如果每个属性值 都是不可再分的最小数据单位,则称R是第一范式的关系
目的:消除实体中列中的重复值或实体的重复属性
例:如职工号,姓名,电话号码组成一个表(一个人可能有一个办公室电话 和一个家里电话号码) 规范成为1NF有三种方法:
一是重复存储职工号和姓名。这样,关键字只能是电话号码。
二是职工号为关键字,电话号码分为单位电话和住宅电话两个属性
三是职工号为关键字,但强制每条记录只能有一个电话号码。
以上三个方法,第一种方法最不可取,按实际情况选取后两种情况。
1NF(第一范式)
特征:无重复列
官方解释:在关系模式R中的每一个具体关系r中,如果每个属性值 都是不可再分的最小数据单位,则称R是第一范式的关系
目的:消除实体中列中的重复值或实体的重复属性
例:如职工号,姓名,电话号码组成一个表(一个人可能有一个办公室电话 和一个家里电话号码) 规范成为1NF有三种方法:
一是重复存储职工号和姓名。这样,关键字只能是电话号码。
二是职工号为关键字,电话号码分为单位电话和住宅电话两个属性
三是职工号为关键字,但强制每条记录只能有一个电话号码。
以上三个方法,第一种方法最不可取,按实际情况选取后两种情况。
3NF(第三范式)
特征:传递依赖
官方解释:如果关系模式R(U,F)中的所有非主属性对任何候选关键字都不存在传递依赖,则称关系R是属于第三范式的。
目的:消除传递依赖
例:如S1(SNO,SNAME,DNO,DNAME,LOCATION) 各属性分别代表学号,
姓名,所在系,系名称,系地址。
关键字SNO决定各个属性。由于是单个关键字,没有部分依赖的问题,肯定是2NF。但这关系肯定有大量的冗余,有关学生所在的几个属性DNO,DNAME,LOCATION将重复存储,插入,删除和修改时也将产生类似以上例的情况。
原因
关系中存在传递依赖造成的。即SNO -> DNO。 而DNO -> SNO却不存在,DNO -> LOCATION, 因此关键字 SNO 对 LOCATION 函数决定是通过传递依赖 SNO -> LOCATION 实现的。也就是说,SNO不直接决定非主属性LOCATION。
解决目地
每个关系模式中不能留有传递依赖。
解决方法
分为两个关系 S(SNO,SNAME,DNO),D(DNO,DNAME,LOCATION)
注意
关系S中不能没有外关键字DNO。否则两个关系之间失去联系。
相关文章:

数据库设计-范式
范式 范式就是数据库的构建规则,目前关系数据库有六种范式:第一范式(1NF)、第二范式(2NF)、第三范式(3NF)、第四范式(4NF)、第五范式(5NF&#x…...

在前端开发中,何时应该使用 jQuery,何时应该使用 Vue.js
如果您是最近才开始进入 Web 前端开发领域的开发人员,那么您可能会听说过 jQuery。jQuery 是一个小巧而功能强大的 JavaScript 库,旨在简化跨浏览器 DOM 操作、事件处理、动画效果和 AJAX 等方面的操作,可以让开发人员更轻松地开发出高质量的…...

Promise类方法
这篇主要讲一下Promise的类方法的基本使用,至于Promise的基本使用这里就不赘述了,之前也有手写过Promise、实现了Promise的核心逻辑。其实我们平时用Promise也挺多的,不过又出现了两个新的语法(ES11,ES12新增了两个&am…...
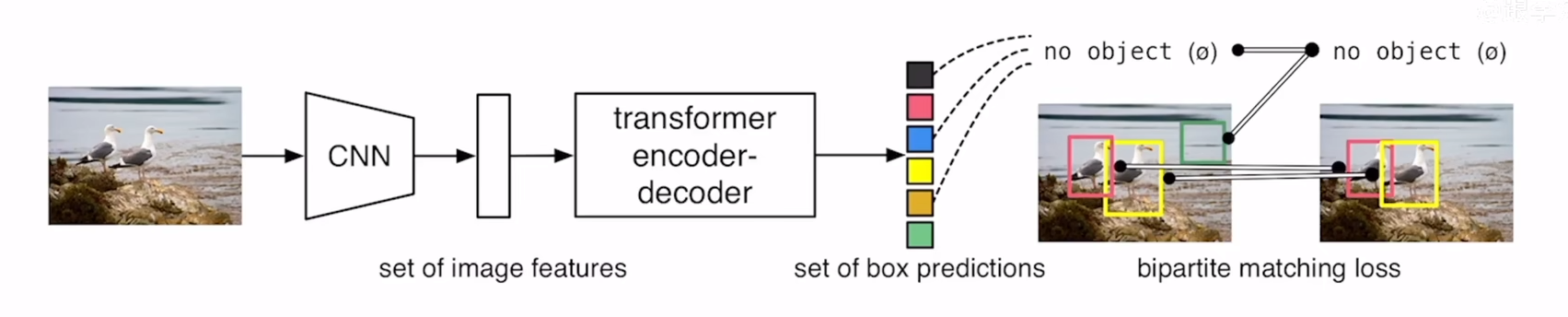
transformer and DETR
RNN 很难并行化处理 Transformer 1、Input向量x1-x4分别乘上矩阵W得到embedding向量a1-a4。 2、向量a1-a4分别乘上Wq、Wk、Wv得到不同的qi、ki、vi(i{1,2,3,4})。 3、使用q1对每个k(ki)做attention得到a1,i(i{1,2,3,4…...
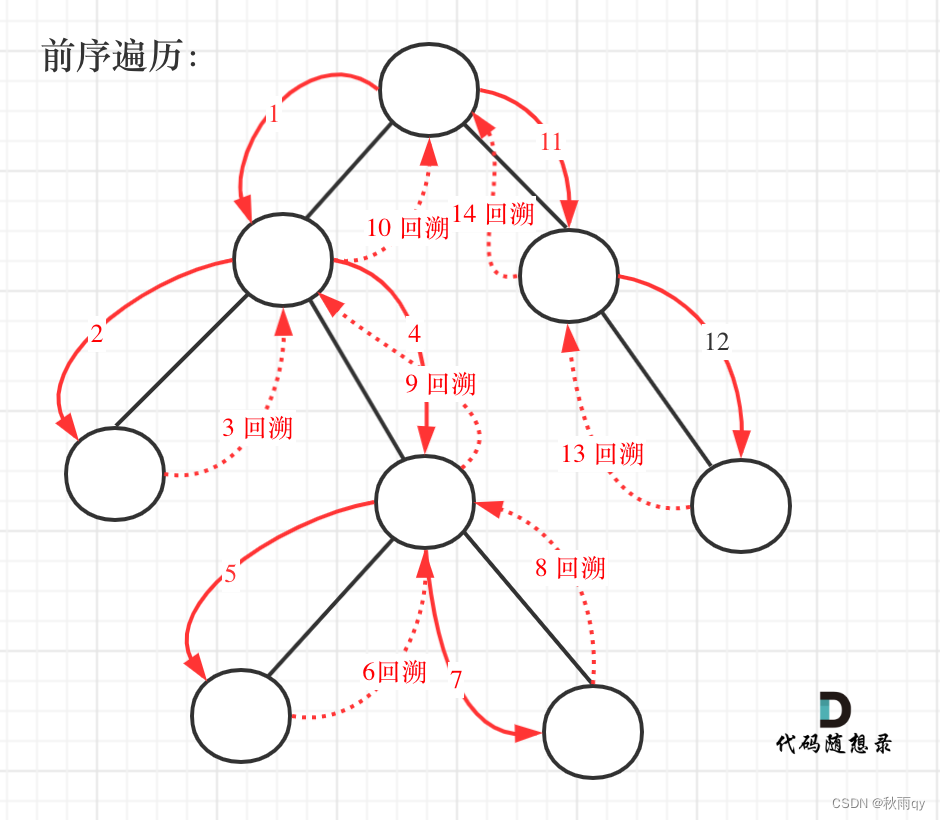
数据结构(六)—— 二叉树(4)回溯
文章目录 一、题1 257 二叉树的所有路径1.1 写法11.2 写法2 一、题 1 257 二叉树的所有路径 1.1 写法1 递归回溯:回溯是递归的副产品,只要有递归就会有回溯 首先考虑深度优先搜索;而题目要求从根节点到叶子的路径,所以需要前序…...
)
JVM基础知识(一)
1.整体架构和组件 1.Class Loader Class Loader(类加载器)负责将.class文件加载到JVM中,并生成对应的Java类对象(Class对象)。Java中有三种类加载器: Bootstram ClassLoader:加载核心类库&…...
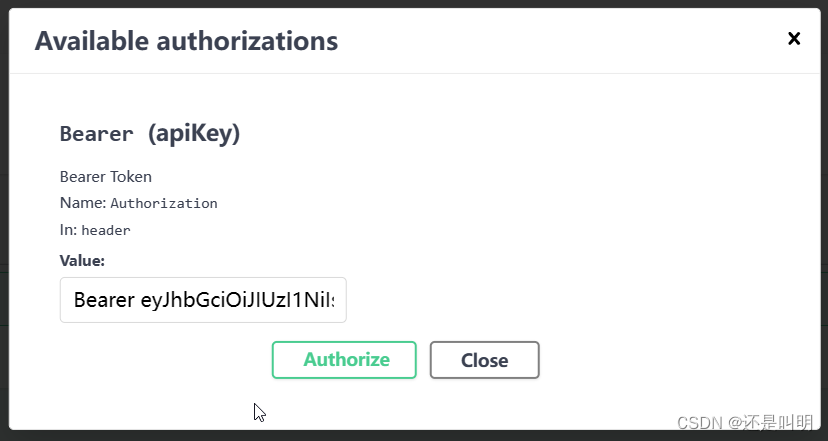
ASP.NET Core Web API用户身份验证
一、JWT介绍 ASP.NET Core Web API用户身份验证的方法有很多,本文只介绍JWT方法。JWT实现了服务端无状态,在分布式服务、会话一致性、单点登录等方面凸显优势,不占用服务端资源。简单来说,JWT的验证过程如下所示: &a…...

785. 快速排序
785. 快速排序 给定你一个长度为 n n n 的整数数列。 请你使用快速排序对这个数列按照从小到大进行排序。 并将排好序的数列按顺序输出。 输入格式 输入共两行,第一行包含整数 n n n。 第二行包含 n n n 个整数(所有整数均在 1 ∼ 1 0 9 1 \th…...

C6678学习-IPC
文章目录 1、简介2、模块MultiProc静态设置(cfg设置)动态设置 IPCNotifyMessageQShareRegion 1、简介 IPC: Inter-Processor Communication 处理器间通信,指提供多处理器环境中的处理器之间的通信、相同处理器不同线程间的通信。包括数据传递…...
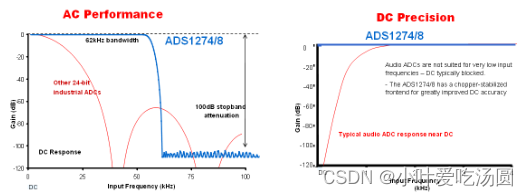
利用 Delte-Sigma ADC简化电路设计
很多时候在电路中选择合适的 ADC可以很大程度上简化前端的电路。这里我们一起来看一个电阻电桥的例子: 这里用到了一只仪表放大器和一只运算放大器,他们实际上主要完成了三个功能: 1. 抑制了 2.5V的共模信号; 2. 将-1…...
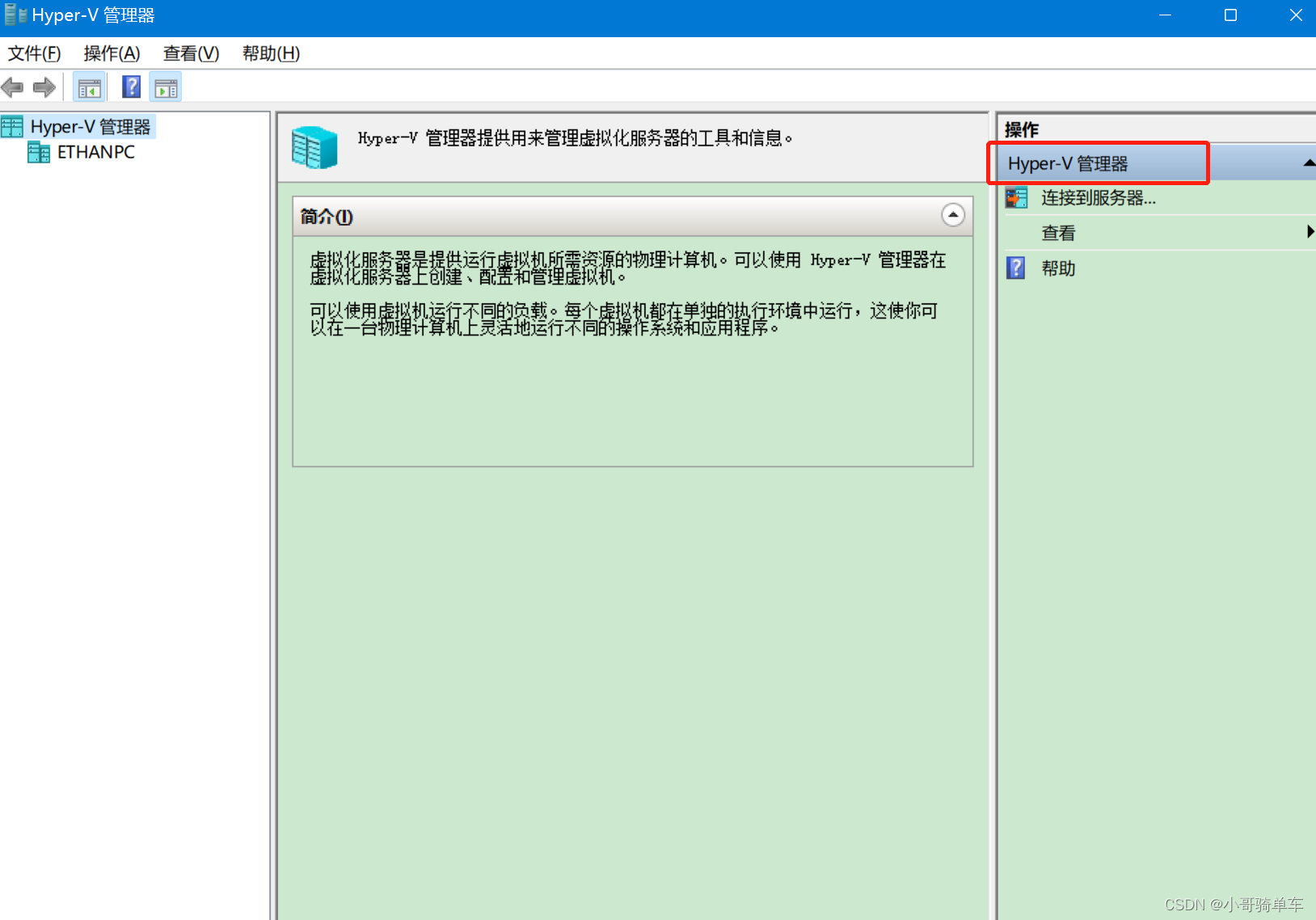
如何在 Windows 11 启用 Hyper-V
准备在本机玩一下k8s,需要先启用 Hyper-V,谁知道这一打开,没有 Hyper-V选项: 1、查看功能截图: 2、以下文件保存记事本,然后重命名为*.bat pushd "%~dp0" dir /b %SystemRoot%\servicing\Packa…...

哈希表企业应用-DNA的字符串检测
DNA的字符串检测-引言 若干年后, ikun DNA 检测部成立,专门对 这些ikun的解析检测 突然发现已经完全控制不了 因为学生已经会了 而且是太会了 所以DNA采用 以下视频测试: ikun必进曲 ikun必经曲 ikun必阶曲 如何感受到了吧!,如果你现在唱跳并且还Rap 还有打篮球 还有铁山靠 那…...

Kafka运维与监控
Kafka运维与监控 Kafka运维与监控一、简介二、运维1.安装和部署安装部署 2.优化参数配置配置文件高级配置分区和副本设置分区数量设置副本数量设置 网络参数调优传输机制设置连接数和缓冲区大小设置 消息压缩和传输设置消息压缩设置消息传输设置 磁盘设置和文件系统分区磁盘容量…...
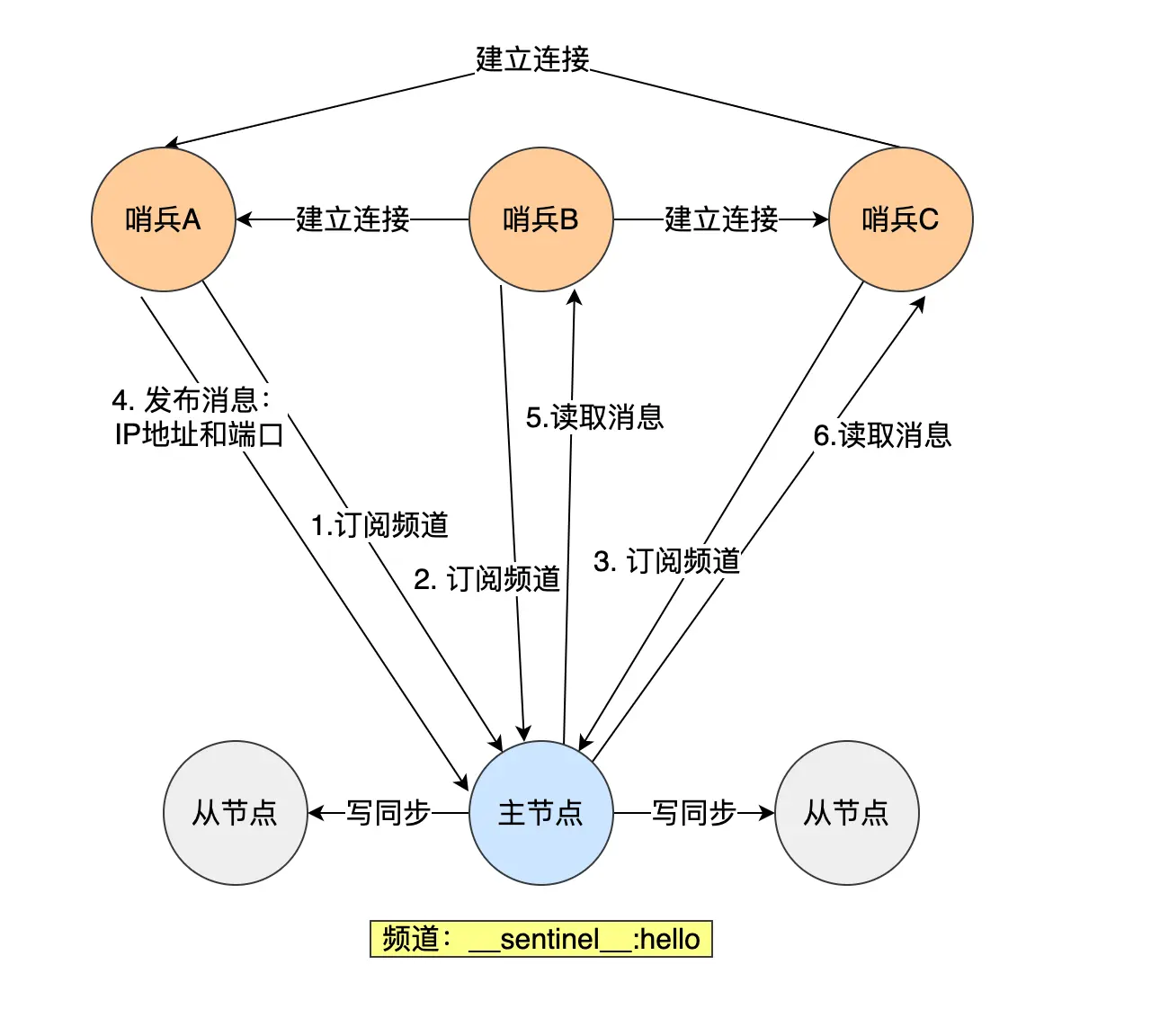
【Redis—哨兵机制】
文章目录 概念哨兵机制如何工作的监控(如何判断主节点真的故障了)哪个哨兵进行主从故障转移?故障转移流程哨兵集群 概念 当进行主从复制时,如果主节点挂掉了,那么没有主节点来服务客户端的写操作请求了,也…...
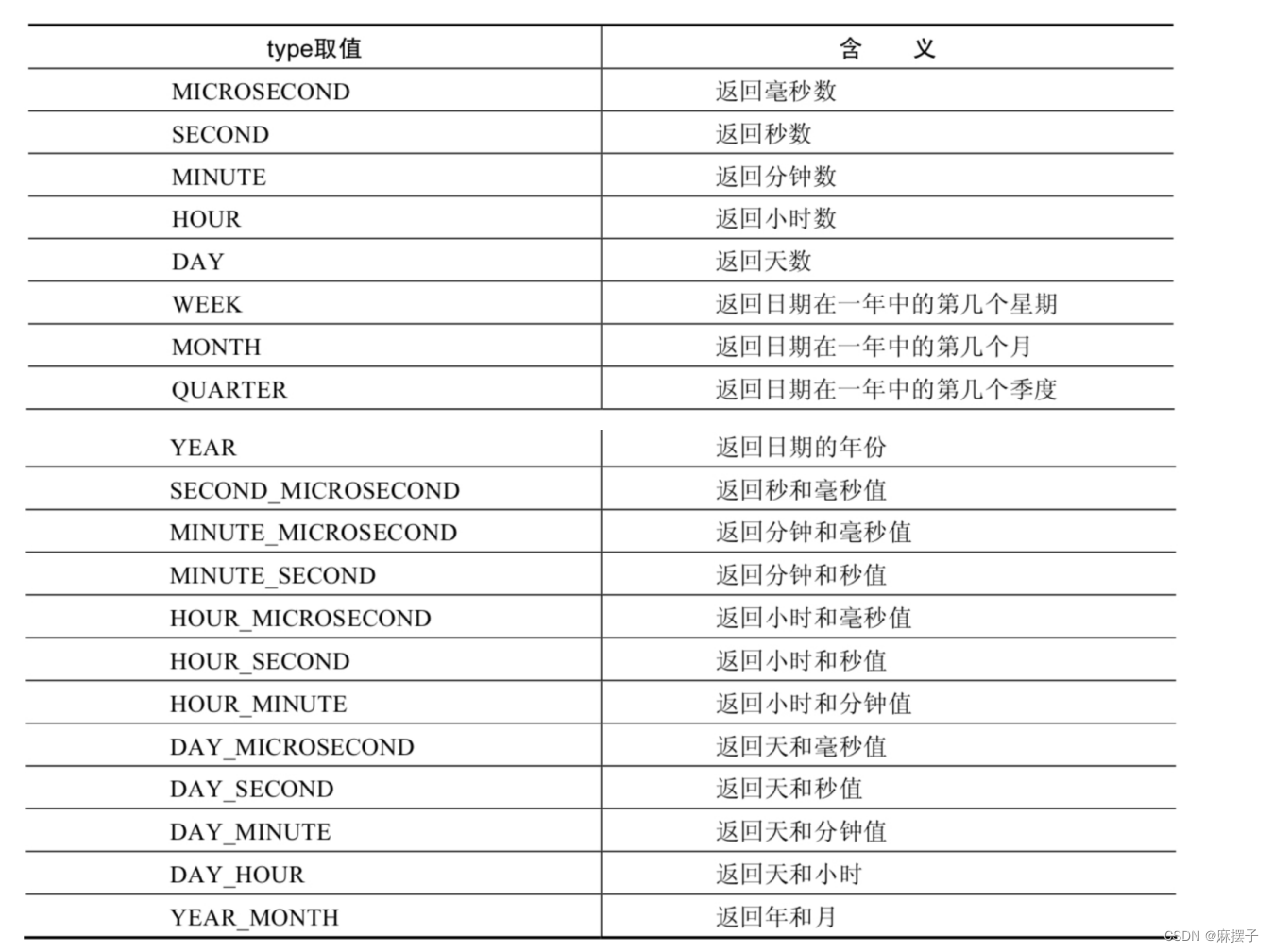
MySQL学习笔记第七天
第07章单行函数 2. 数值函数 2.4 指数函数、对数函数 函数用法POW(x,y),POWER(X,Y)返回x的y次方EXP(X)返回e的x次方,其中e是一个常数,2.718281828459045LN(X),LOG(X)返回以e为底的X的对数,当x<0时,返…...

中级软件设计师备考---程序设计语言和法律法规知识
目录 需要掌握的程序语言特点法律法规知识---保护期限法律法规知识---知识产权人确定法律法规知识---侵权判定标准化基础知识 需要掌握的程序语言特点 Fortran语言:科学计算、执行效率高Pascal语言:为教学而开发的、表达能力强,演化出了Delp…...
Leetcode434. 字符串中的单词数
Every day a leetcode 题目来源:434. 字符串中的单词数 解法1:istringstream 我们知道,C默认通过空格(或回车)来分割字符串输入,即区分不同的字符串输入。 istringstream类用于执行C风格的串流的输入操…...

C++ cmake工程引入qt6和Quick 教程
目录标题 前言QML简介锻炼C水平 cmake修改方法方式一(qt6_add_resources)方式二 (qt_add_qml_module ) 其他相关知识为什么会有_other_files?qt_standard_project_setup() 函数qt_add_qml_module() 和 qt6_add_resources()的方式差异const QU…...
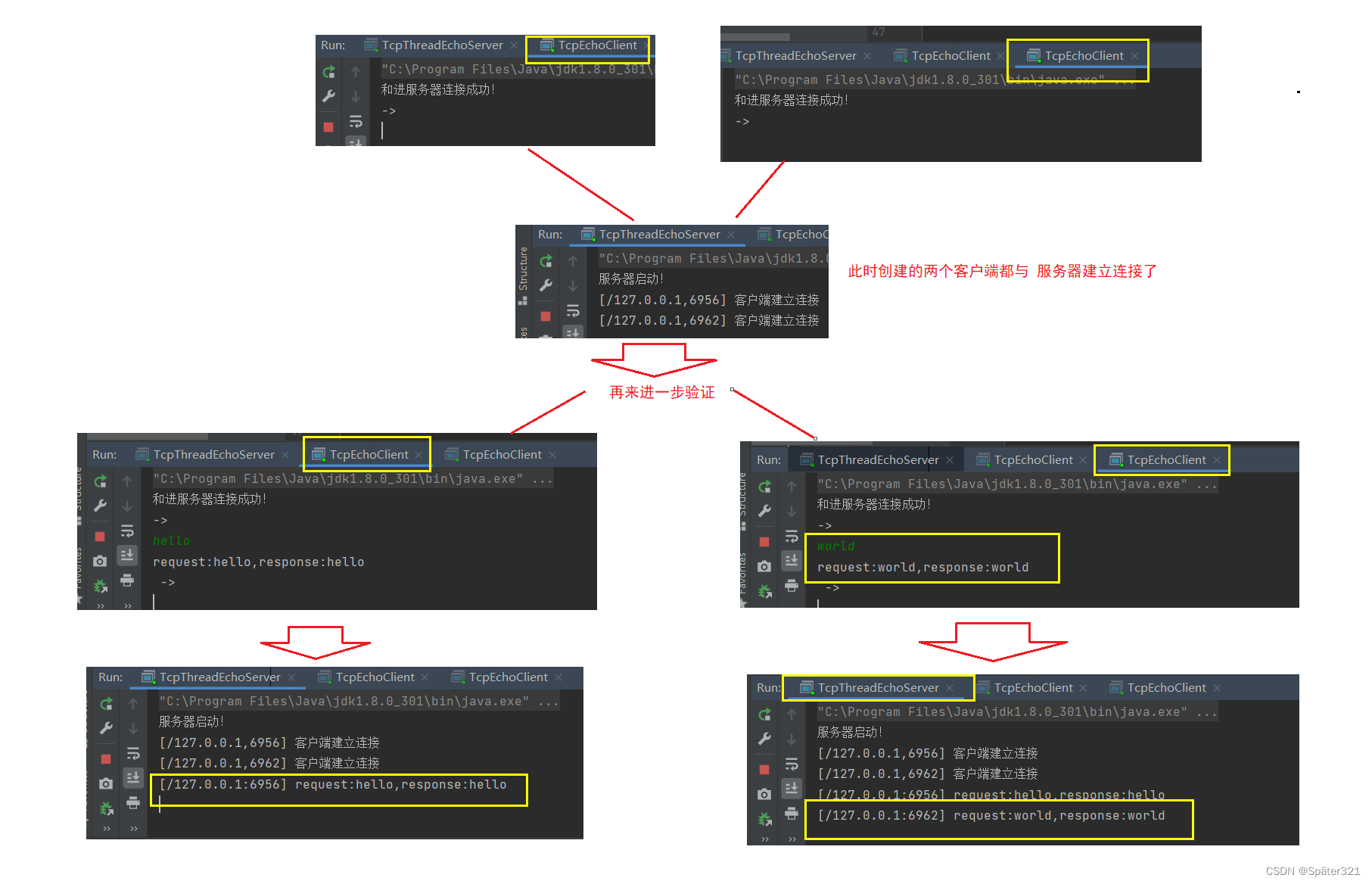
JavaEE - 网络编程
一、网络编程基础 为什么需要网络编程? 用户在浏览器中,打开在线视频网站,如优酷看视频,实质是通过网络,获取到网络上的一个视频资源。 与本地打开视频文件类似,只是视频文件这个资源的来源是网络。 相比本…...
【Android车载系列】第11章 系统服务-SystemServer自定义服务
1 编写自定义系统服务 1.1 AIDL接口定义 系统源码目录/frameworks/base/core/java/android/app/下新建AIDL接口IYvanManager.aidl package android.app;/** * 目录:/frameworks/base/core/java/android/app/IYvanManager.aidl */ interface IYvanManager{String …...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
