利用 Delte-Sigma ADC简化电路设计
很多时候在电路中选择合适的 ADC可以很大程度上简化前端的电路。这里我们一起来看一个电阻电桥的例子:
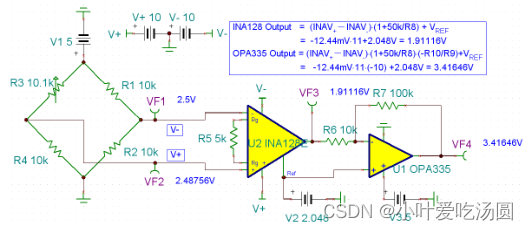
这里用到了一只仪表放大器和一只运算放大器,他们实际上主要完成了三个功能:
1. 抑制了 2.5V的共模信号;
2. 将-12.44mV的差模信号放大了 110倍,从而满足了 ADC采样精度的要求;
3. 虽然电桥输出的信号都是单极性(正电平)的,但是其差模信号 -12.44mV 到12.56mV是双极性的。运放电路给该双极性信号加入了 2.048V的直流偏置,使得最大化利用了 0-4.096V输入 ADC的动态范围;
所以如果我们能找到一种 ADC,拥有全差分输入(提供完整的共模抑制能力),并拥有超高的精度,我们就有可能无需 INA进行共模抑制和电平抬升,无需两级放大就能够完成在25mV中获得 2000个读数的要求,就是说该 ADC的最小分辨率要小于 12.5uV!
(1) 用△-∑ ADC完成整个信号链的工作
在电阻电桥中,当 R3这个可变电阻器的阻值从 9.9k变化到 10.1k的过程中,输出的差模信号为 12.56mV到-12.44mV,也就是说在 0.2k欧姆的电阻变化过程中,可检测的信号变化范围为 25mV。如果期望的精度为 0.1欧姆,即需要 2000个读数,即在 25mV的范围内需要2000个读数,即每个读数为 12.5uV。
以 ADS1232为例,它是 24位 5V满量程输入的 ADC,由下表可以看到当其数据吞吐率为10SPS,内部 PGA设定为 1时,其输入级峰峰值噪声仅为 1.79uV。

此时,ADS1232的无噪声位数可以达到 21.4位,这里我们取 2^20约合 10^6来计算ADS1232每个 LSB的大小为:1LSB=5V/10^6=5uV < 12.5uV。在电桥 25mV的满量程差模输出中可以得到 5000个读数,远远满足要求。因此,电路可以简化为:

虽然理论上我们可以使用 ADS1232完成设计,但是在系统设计中,控制系统噪声(包括器件噪声,辐射噪声和传导噪声等)的峰峰值小于 12.5uV是非常困难的事情。这时,我们可以利用 ADS1232内部的 PGA,把输入差模信号放大(可选倍数为 1,2,4…128),比如我们把输入的 25mV差模信号通过内部 PGA放大 64倍,得到 1.6V的有用差模信号,我们的系统噪声只需小于 1.6V/2000=800uV就可以完成工作了,这对系统设计的要求降低了许多,特别是在省略了大量的运放和电阻器后,噪声源减少,更有利于减少系统噪声。从芯片数据表我们可以看到,在 PGA倍数增大后,ADS1232的输入级噪声变为:125nV*64=8uV。
在使用 PGA后,我们对 ADC的位数要求可以降低,现在可以使用 16位的满量程输入为5V的 ADS1146来完成设计,此时 ADS1146的 1LSB=5V/65536=76uV,从放大后的 1.6V差模信号中可以获得 1.6V/76uV=20,000个数据!同时,ADS1146也拥有完整的差分输入级,可以完成整个信号链的工作。
(2) 利用 ADS1147完成对 3线制 RTD电阻的测量

ADS1147(16位)和 ADS1247(24位)是内建电流源的△-∑ ADC, 这类 ADC专为 RTD等需要电流源激励的传感器设计,其全差分输入,PGA放大器和超高的精度帮助我们省下了一大堆运放和电阻。
除了压力信号,温度信号这种变化缓慢的信号需要高精度测量,还有一些动态范围大的低频交流小信号需要被稍高的采样率高精度采集,比如振动信号,地震信号的采集,这时几十或者几百 Hz的吞吐率已经难以满足要求,而 TI推出的 ADS127x,业界最快的兼顾直流和交流精度的∑-△型 ADC,就非常适合这类需求。
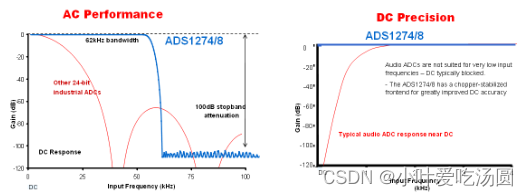
如上图,在交流精度方面,和相近直流精度的工业用∑-△型 ADC相比,ADS127x拥有更宽的频率响应,可以对 62KHz带宽的模拟输入信号采样;而在直流精度方面,和相同采样率的音频∑-△型 ADC相比,ADS127x又充分保留了测量的直流精度。
相关文章:

利用 Delte-Sigma ADC简化电路设计
很多时候在电路中选择合适的 ADC可以很大程度上简化前端的电路。这里我们一起来看一个电阻电桥的例子: 这里用到了一只仪表放大器和一只运算放大器,他们实际上主要完成了三个功能: 1. 抑制了 2.5V的共模信号; 2. 将-1…...
如何在 Windows 11 启用 Hyper-V
准备在本机玩一下k8s,需要先启用 Hyper-V,谁知道这一打开,没有 Hyper-V选项: 1、查看功能截图: 2、以下文件保存记事本,然后重命名为*.bat pushd "%~dp0" dir /b %SystemRoot%\servicing\Packa…...

哈希表企业应用-DNA的字符串检测
DNA的字符串检测-引言 若干年后, ikun DNA 检测部成立,专门对 这些ikun的解析检测 突然发现已经完全控制不了 因为学生已经会了 而且是太会了 所以DNA采用 以下视频测试: ikun必进曲 ikun必经曲 ikun必阶曲 如何感受到了吧!,如果你现在唱跳并且还Rap 还有打篮球 还有铁山靠 那…...

Kafka运维与监控
Kafka运维与监控 Kafka运维与监控一、简介二、运维1.安装和部署安装部署 2.优化参数配置配置文件高级配置分区和副本设置分区数量设置副本数量设置 网络参数调优传输机制设置连接数和缓冲区大小设置 消息压缩和传输设置消息压缩设置消息传输设置 磁盘设置和文件系统分区磁盘容量…...
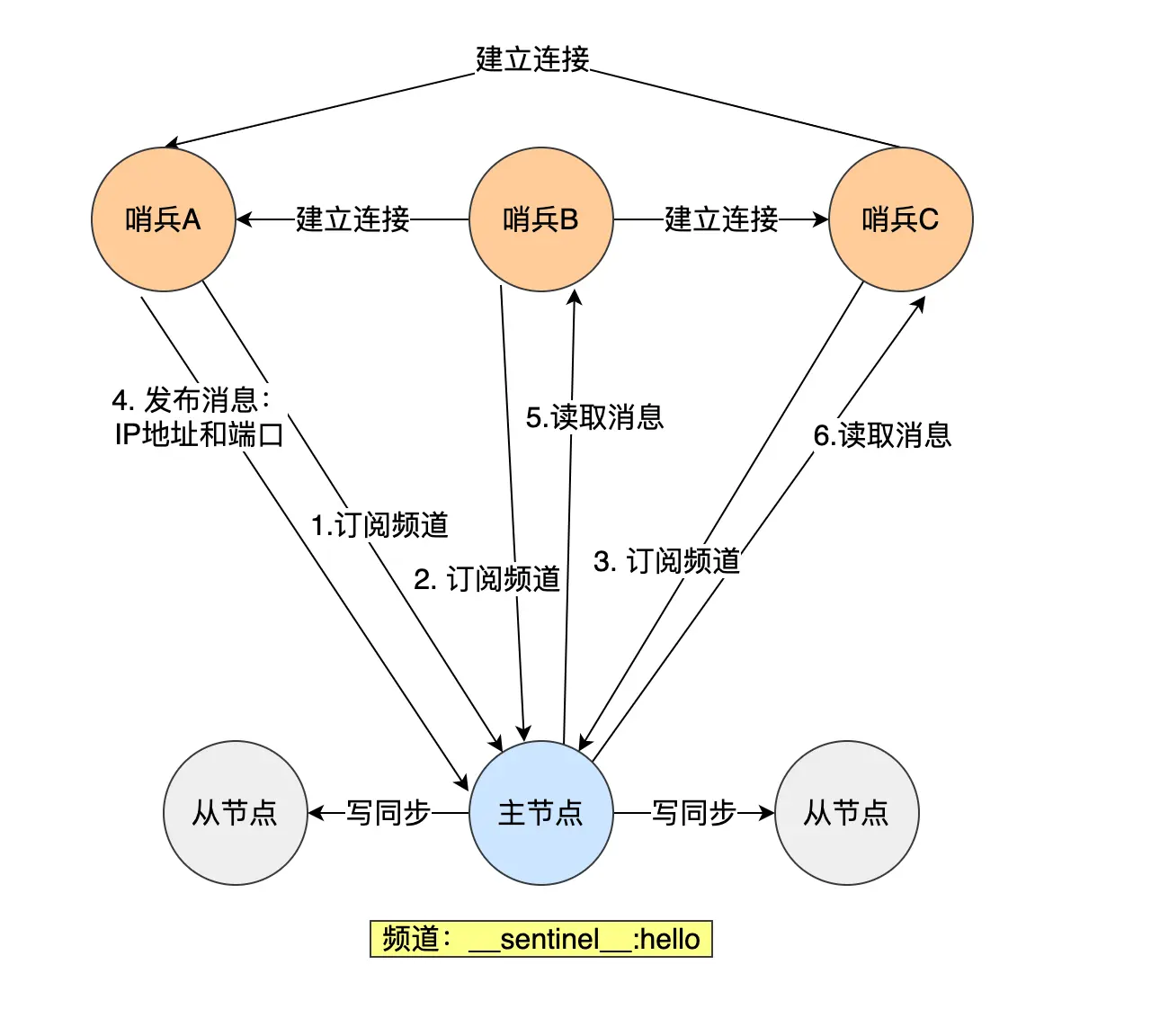
【Redis—哨兵机制】
文章目录 概念哨兵机制如何工作的监控(如何判断主节点真的故障了)哪个哨兵进行主从故障转移?故障转移流程哨兵集群 概念 当进行主从复制时,如果主节点挂掉了,那么没有主节点来服务客户端的写操作请求了,也…...
MySQL学习笔记第七天
第07章单行函数 2. 数值函数 2.4 指数函数、对数函数 函数用法POW(x,y),POWER(X,Y)返回x的y次方EXP(X)返回e的x次方,其中e是一个常数,2.718281828459045LN(X),LOG(X)返回以e为底的X的对数,当x<0时,返…...

中级软件设计师备考---程序设计语言和法律法规知识
目录 需要掌握的程序语言特点法律法规知识---保护期限法律法规知识---知识产权人确定法律法规知识---侵权判定标准化基础知识 需要掌握的程序语言特点 Fortran语言:科学计算、执行效率高Pascal语言:为教学而开发的、表达能力强,演化出了Delp…...
Leetcode434. 字符串中的单词数
Every day a leetcode 题目来源:434. 字符串中的单词数 解法1:istringstream 我们知道,C默认通过空格(或回车)来分割字符串输入,即区分不同的字符串输入。 istringstream类用于执行C风格的串流的输入操…...

C++ cmake工程引入qt6和Quick 教程
目录标题 前言QML简介锻炼C水平 cmake修改方法方式一(qt6_add_resources)方式二 (qt_add_qml_module ) 其他相关知识为什么会有_other_files?qt_standard_project_setup() 函数qt_add_qml_module() 和 qt6_add_resources()的方式差异const QU…...
JavaEE - 网络编程
一、网络编程基础 为什么需要网络编程? 用户在浏览器中,打开在线视频网站,如优酷看视频,实质是通过网络,获取到网络上的一个视频资源。 与本地打开视频文件类似,只是视频文件这个资源的来源是网络。 相比本…...
【Android车载系列】第11章 系统服务-SystemServer自定义服务
1 编写自定义系统服务 1.1 AIDL接口定义 系统源码目录/frameworks/base/core/java/android/app/下新建AIDL接口IYvanManager.aidl package android.app;/** * 目录:/frameworks/base/core/java/android/app/IYvanManager.aidl */ interface IYvanManager{String …...

Lerna
Lerna Lerna是一个优化基于gitnpm的多pagkage项目的管理工具 解决的痛点 痛点一:重复操作 多Package本地link多Package依赖安装多Package单元测试多Package代码提交多Package代码发布 痛点二:版本一致性 发布时版本一 致性发布后相互依赖版本升级 package越多,管…...

迁移学习 pytorch
迁移学习(Transfer Learning)是通过使用一个预训练模型来快速训练一个新的网络模型,通常应用于数据集较小或计算资源较少的情况下。在 PyTorch 中,由于 torchvision 库中已经内置了一些经典的预训练模型,因此我们可以通过简单的调用函数来实现迁移学习。 下面是一个基于 …...
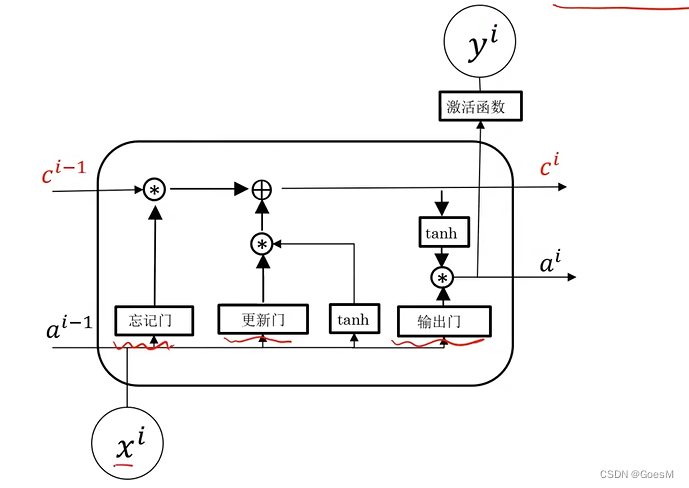
【python】keras包:深度学习( RNN循环神经网络 Recurrent Neural Networks)
RNN循环神经网络 应用: 物体移动位置预测、股价预测、序列文本生成、语言翻译、从语句中自动识别人名、 问题总结 这类问题,都需要通过历史数据,对未来数据进行预判 序列模型 两大特点 输入(输出)元素具有顺序关系…...

vue框架快速入门
vue 1、第一个Vue程序1.1、什么是Vue程序1.2、为什么要使用MVVM1.3、Vue1.4、第一个vue程序 2、基础语法2.1、v-bind2.2、v-if, v-else2.3、v-for2.4、v-on 3、Vue表单双绑、组件3.1、什么是双向数据绑定3.2、在表单中使用双向数据绑定3.3、什么是组件 4、Axios异步…...
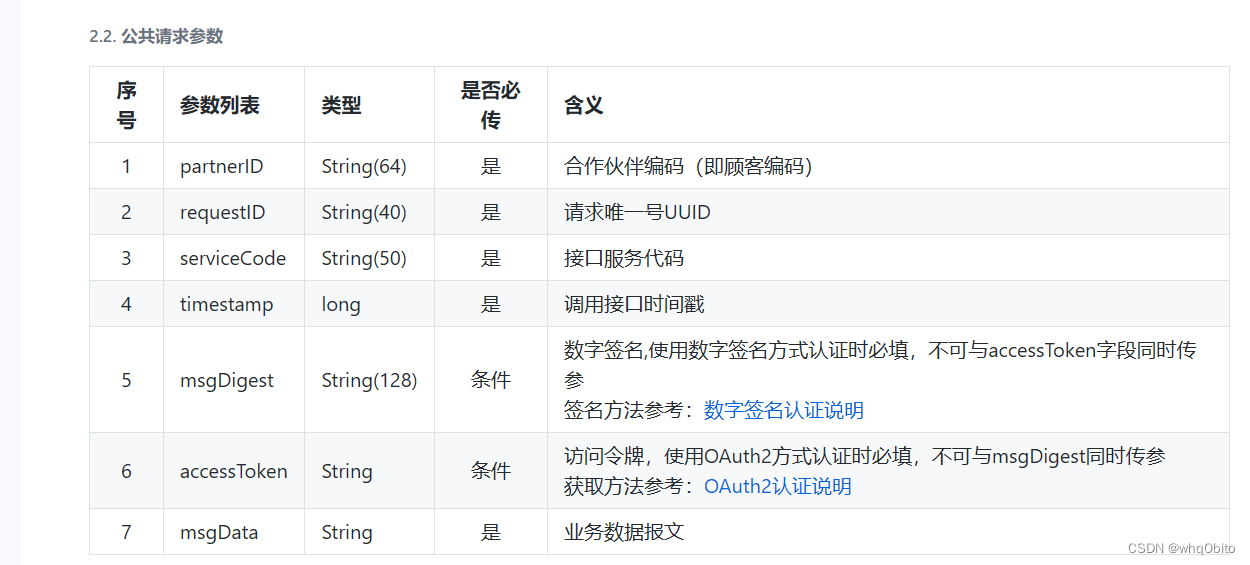
Java连接顺丰开放平台
今天使用Java去访问顺丰的开放平台时,JSON转换一直不成功,最终发现是 可以看到这里是 "apiResultData": "{\"success\": .........它是以 " 开头的!!!如果是对象的话,那么…...

前端三剑客 - HTML
前言 前面都是一些基础的铺垫,现在就正式进入到web开发环节了。 我们的目标就是通过学习 JavaEE初阶,搭建出一个网站出来。 一个网站分成两个部分: 前端(客户端) 后端(服务器) 通常这里的客户端…...
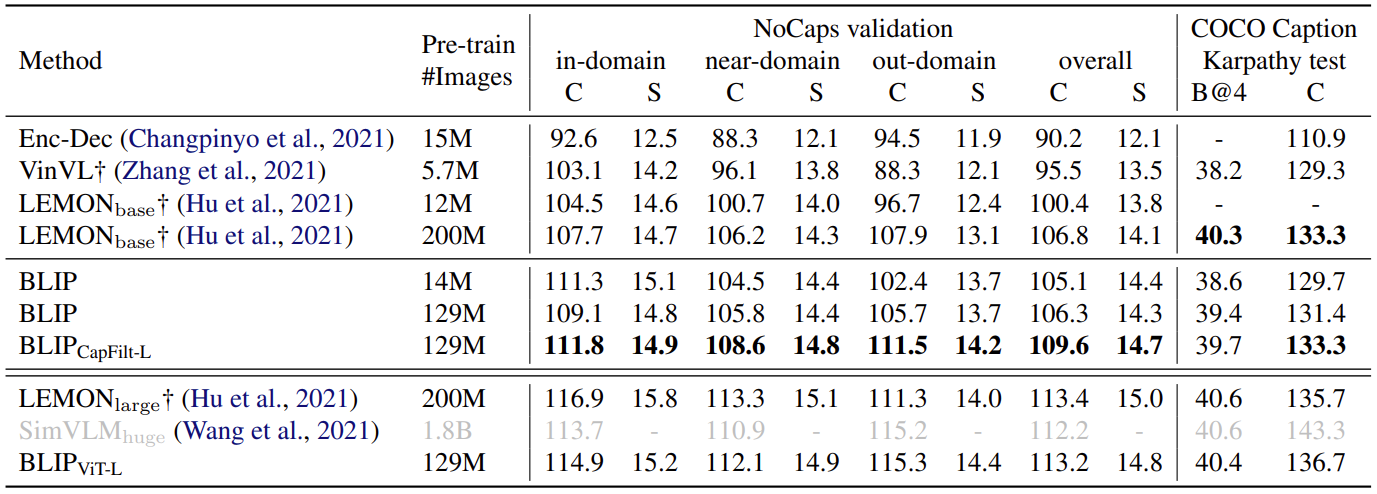
【计算机视觉 | 自然语言处理】BLIP:统一视觉—语言理解和生成任务(论文讲解)
文章目录 一、前言二、试玩效果三、研究背景四、模型结构五、Pre-training objectives六、CapFilt架构七、Experiment八、结论 一、前言 今天我们要介绍的论文是 BLIP,论文全名为 Bootstrapping Language-Image Pre-training for Unified Vision-Language Understa…...
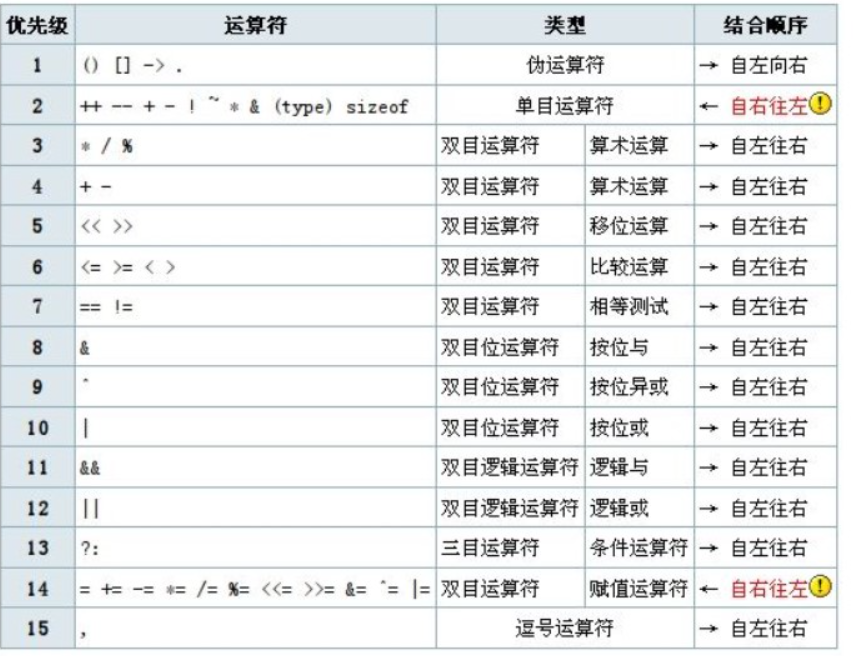
c++基础-运算符
目录 1关系运算符 2运算符优先级 3关系表达式的书写 代码实例: 下面是面试中可能遇到的问题: 1关系运算符 C中有6个关系运算符,用于比较两个值的大小关系,它们分别是: 运算符描述等于!不等于<小于>大于<…...

美术馆c++
题目: 杜老师非常喜欢玩一种叫做“美术馆”的数字游戏,蜗蜗看了之后决定也来试一试,他改编了这个游戏,规则如下: 有一个 n� 行 m� 列的方格,每一个格子中有一个数,数字…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
