智能优化算法:浣熊优化算法-附代码
智能优化算法:浣熊优化算法
文章目录
- 智能优化算法:浣熊优化算法
- 1.浣熊优化算法
- 1.1 初始化
- 1.2 阶段一:狩猎和攻击(探索阶段)
- 2.实验结果
- 3.参考文献
- 4. Matlab
摘要:浣熊优化算法(Coati Optimization Algorithm(COA)),是于2022年提出的一种基于浣熊行为的优化算法,该算法通过模拟浣熊猎食行为来进行寻优,具有寻优能力强,收敛速度快等特点
1.浣熊优化算法
1.1 初始化
与其他优化算法类似,在寻优空间里随机初始化种群:
x i , j = l b j + r ⋅ ( u b j − l b j ) (2) x_{i, j}=l b_j+r \cdot\left(u b_j-l b_j\right) \tag{2} xi,j=lbj+r⋅(ubj−lbj)(2)
其中 x i , j x_{i,j} xi,j为个体, l b j lb_j lbj为寻优下边界, u b j ub_j ubj为寻优上边界, r r r为[0,1]之间的随机数。
1.2 阶段一:狩猎和攻击(探索阶段)
在搜索空间中更新coatis种群的第一阶段是基于模拟它们攻击鬣蜥(Iguana)时的策略进行建模的。在这一策略中,一群coatis爬上树去够一只鬣蜥并吓唬它。其他几只coatis在树下等待,直到鬣蜥摔倒在地。鬣蜥落地后,coatis攻击并猎杀它。这种策略导致coatis移动到搜索空间的不同位置,这表明了COA在解决问题空间的全局搜索中的探索能力。
在COA设计中,假设种群中最好成员的位置是鬣蜥的位置。也有人假设,一半的鬣蜥爬上树,另一半等待鬣蜥掉到地上。因此,使用等式(4)对从树上升起的涂层的位置进行数学模拟。
X i P 1 : x i , j P 1 = x i , j + r ⋅ ( Iguana j − I ⋅ x i , j ) , for i = 1 , 2 , … , ⌊ N 2 ⌋ a n d j = 1 , 2 , … , m . (4) X_i^{P 1}: x_{i, j}^{P 1}=x_{i, j}+r \cdot\left(\text { Iguana }_j-I \cdot x_{i, j}\right), \text { for } i=1,2, \ldots,\left\lfloor\frac{N}{2}\right\rfloor \\and j=1,2, \ldots, m. \tag{4} XiP1:xi,jP1=xi,j+r⋅( Iguana j−I⋅xi,j), for i=1,2,…,⌊2N⌋andj=1,2,…,m.(4)
鬣蜥摔倒在地后,它被放置在搜索空间中的一个随机位置。基于这个随机位置,地面上的涂层在搜索空间中移动,这是使用等式(5)和(6)模拟的。
Iguana G : Iguana a j G = l b j + r ⋅ ( u b j − l b j ) , j = 1 , 2 , … , m , (5) \begin{aligned} & \text { Iguana }^G: \text { Iguana } a_j^G=l b_j+r \cdot\left(u b_j-l b_j\right), j=1,2, \ldots, m \text {, } \end{aligned}\tag{5} Iguana G: Iguana ajG=lbj+r⋅(ubj−lbj),j=1,2,…,m, (5)
X i p 1 : x i , j P 1 = { x i , j + r ⋅ ( Iguana j j G − I ⋅ x i , j ) , F Iguana G < F i , x i , j + r ⋅ ( x i , j − Iguana j G ) , else, for i = ⌊ N 2 ⌋ + 1 , ⌊ N 2 ⌋ + 2 , … , N and j = 1 , 2 , … , m . (6) \begin{aligned} & X_i^{p 1}: x_{i, j}^{P 1}=\left\{\begin{array}{cl} x_{i, j}+r \cdot\left(\text { Iguana } j_j^G-I \cdot x_{i, j}\right), & F_{\text {Iguana }}^G<F_i, \\ x_{i, j}+r \cdot\left(x_{i, j}-\text { Iguana }_j^G\right), & \text { else, } \end{array}\right. \\ & \text { for } i=\left\lfloor\frac{N}{2}\right\rfloor+1,\left\lfloor\frac{N}{2}\right\rfloor+2, \ldots, N \text { and } j=1,2, \ldots, m \text {. } \\ & \end{aligned}\tag{6} Xip1:xi,jP1={xi,j+r⋅( Iguana jjG−I⋅xi,j),xi,j+r⋅(xi,j− Iguana jG),FIguana G<Fi, else, for i=⌊2N⌋+1,⌊2N⌋+2,…,N and j=1,2,…,m. (6)
如果更新后的个体更优则更新当前个体,否则保持原状:
X i = { X i P 1 , F i P 1 < F i X i , else. (7) X_i=\left\{\begin{aligned} X_i^{P 1}, & F_i^{P 1}<F_i \\ X_i, & \text { else. } \end{aligned}\right. \tag{7} Xi={XiP1,Xi,FiP1<Fi else. (7)
这里 X i P 1 X_i^{P1} XiP1是更新后的新位置, I g u a n a Iguana Iguana为猎物鬣蜥的位置, r r r为[0,1]之间的随机数。I为随机选择的1或者2。
1.3 阶段二:逃离捕食者(开发阶段)
更新coatis在搜索空间中的位置的过程的第二阶段是基于coatis遇到捕食者和逃离捕食者时的自然行为进行数学建模的。当捕食者攻击一只coatis时,它会从自己的位置逃跑。Coati在这一战略中的举措使其处于接近当前位置的安全位置,这表明了COA在本地搜索中的局部搜索能力。
为了模拟这种行为,基于等式(8)和(9),在每个coatis所在的位置附近生成随机位置。
l b j local = l b j t , u b j local = u b j t , where t = 1 , 2 , … , T (8) \begin{gathered} l b_j^{\text {local }}=\frac{l b_j}{t}, u b_j^{\text {local }}=\frac{u b_j}{t}, \text { where } t=1,2, \ldots, T \end{gathered}\tag{8} lbjlocal =tlbj,ubjlocal =tubj, where t=1,2,…,T(8)
X i P 2 : x i , j P 2 = x i , j + ( 1 − 2 r ) ⋅ ( l b j local + r ⋅ ( u b j local − l b j local ) ) , i = 1 , 2 , … , N , j = 1 , 2 , … , m (9) \begin{gathered} X_i^{P 2}: x_{i, j}^{P 2}=x_{i, j}+(1-2 r) \cdot\left(l b_j^{\text {local }}+r \cdot\left(u b_j^{\text {local }}-l b_j^{\text {local }}\right)\right), \\ i=1,2, \ldots, N, j=1,2, \ldots, m \end{gathered}\tag{9} XiP2:xi,jP2=xi,j+(1−2r)⋅(lbjlocal +r⋅(ubjlocal −lbjlocal )),i=1,2,…,N,j=1,2,…,m(9)
其中t 为迭代次数,如果更新后的个体更优则更新当前个体,否则保持原状:
X i = { X i P 2 , F i P 2 < F i X i , else (10) X_i=\left\{\begin{aligned} X_i^{P 2}, & F_i^{P 2}<F_i \\ X_i, & \text { else } \end{aligned}\right.\tag{10} Xi={XiP2,Xi,FiP2<Fi else (10)
算法流程图如下:

2.实验结果

3.参考文献
[1]Dehghani Mohammad,Montazeri Zeinab,Trojovská Eva,Trojovský Pavel. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems[J]. Knowledge-Based Systems,2023,259.
uristic algorithm for solving optimization problems[J]. Knowledge-Based Systems,2023,259.
4. Matlab
相关文章:

智能优化算法:浣熊优化算法-附代码
智能优化算法:浣熊优化算法 文章目录 智能优化算法:浣熊优化算法1.浣熊优化算法1.1 初始化1.2 阶段一:狩猎和攻击(探索阶段) 2.实验结果3.参考文献4. Matlab 摘要:浣熊优化算法(Coati Optimizat…...
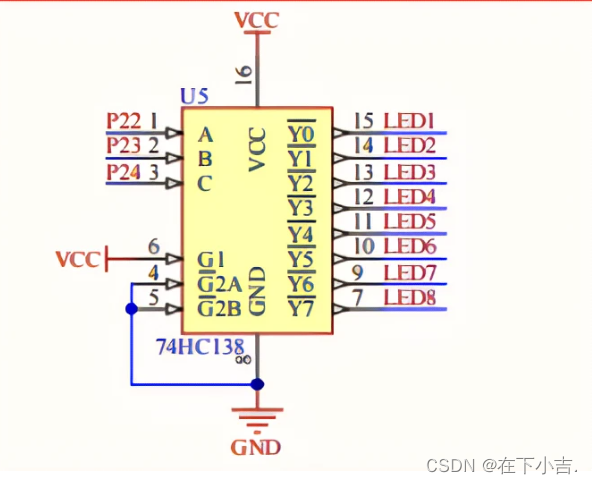
【51单片机】数码管显示(样例展示以及异常分析)
🎊专栏【51单片机】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 大一同学小吉,欢迎并且感谢大家指出我的问题🥰 ⭐数码管 比如要显示“6”,那么下面图片中,AFEDCG=1,B=0 对应到数码管上,就是 ⭐原理 🎊P22~P24控制LED1~...

Android InputChannel事件发送接收系统分析
本文基于Android12。 InputChannel表示其他进程通过文件描述符传递输入事件到View的通道,因为需要跨进程传输,实现了Parcelable序列化接口,所以也能够理解Java层的InputChannel后面为什么使用copyTo()方法初始化。 输入事件的接收方是View&…...
-- LocalDate()类)
Java时间类(五)-- LocalDate()类
目录 引言: 1. LocalDate的概述: 2. LocalDate的常用方法: 引言: (1)Date存在的缺陷: 如果不格式化,打印出的日期可读性差://获取当前时间Date date = new Date();System.out.println("date = " + date); //date = Wed May 03 22:30:24 CST...
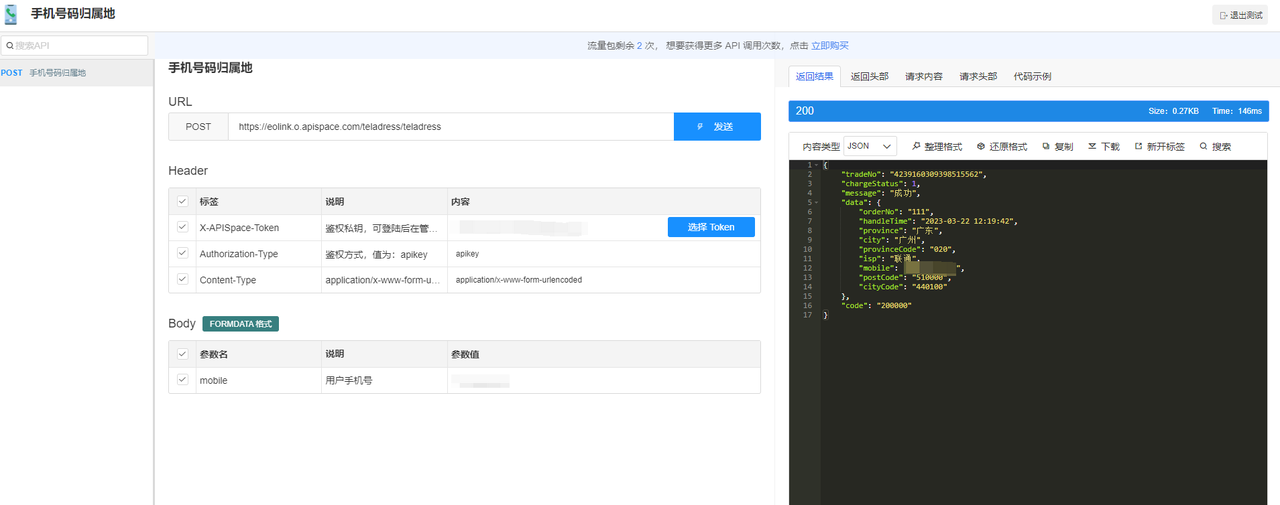
用手机号码归属地 API 开发的应用推荐
引言 手机号码归属地 API是一种提供手机号码归属地信息的接口,通过该接口,可以获取手机号码所属的省份、城市、运营商等信息。它可以帮助企业更好地了解客户,为个性化推荐和精准广告投放提供数据支持。作为一种数据服务,手机号码…...
测试从业第 3 年,我看到了终点......
先说明,今天的内容,是写给想成为高级测试开发、自动化测试专家的人看的,因为,它可能颠覆你的认知。 众所周知,如今无论是大厂还是中小厂,自动化测试基本是标配了,毕竟像双11、618 这种活动中庞…...

结巴分词原理分析
结巴分词器工作原理 结巴分词是一款python写成的开源中文分词器,分词过程大致如下: 首先,结巴使用正则表达式将输入文本切割成若干中文块,接着对每个中文块B做处理,将B转成有向无环图(DAG)。DAG是以{key:list[i,j...…...

JavaEE 第三-四周
计算机Z20-第3-4周作业 总分:100分 得分:74.2分 1 . 填空题 简单 5分 在web.xml文件中,<url-pattern>/xxxxServlet</url-pattern>中的第一个‘/’表示__________。 学生答案 当前web应用程序的根目录 2 . 填空题 简…...
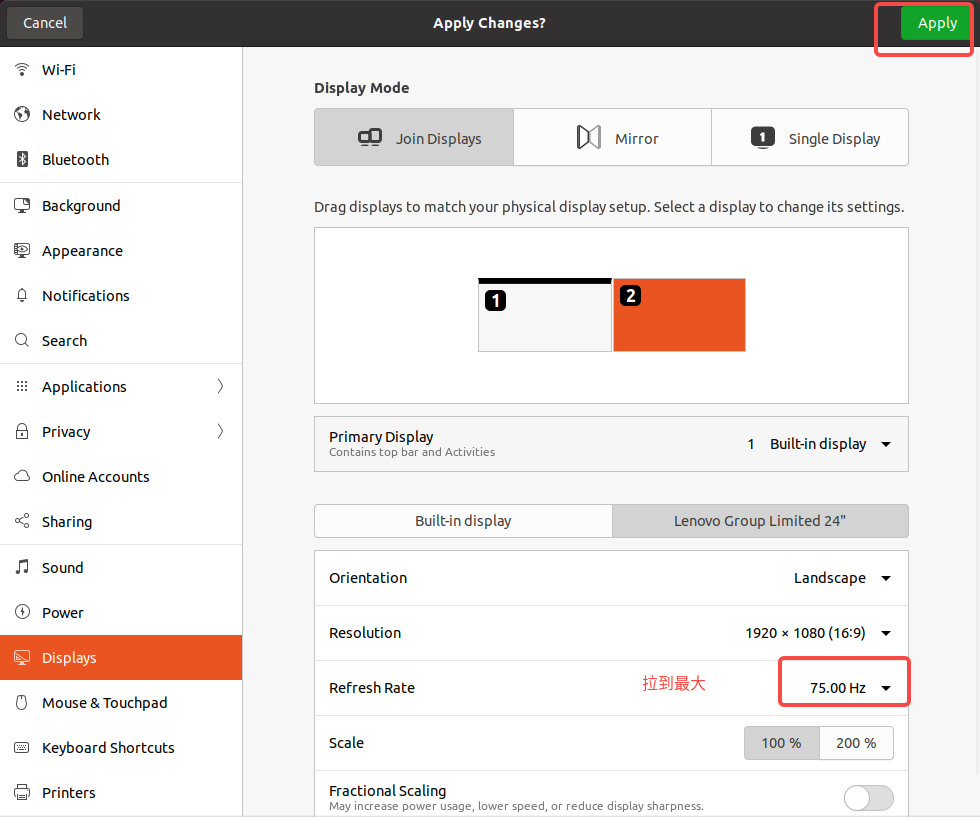
Ububtu20.04 无法连接外屏(显卡驱动问题导致)
Ububtu20.04 无法显示第二个屏幕(显卡驱动问题) Ububtu20.04 无法显示第二个屏幕(显卡驱动问题) Ububtu20.04 无法显示第二个屏幕(显卡驱动问题) 1. 问题描述2. 解决方案 1. 问题描述 一开始我的ububt…...
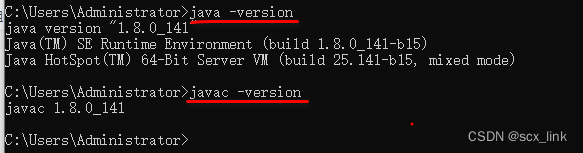
配置JDK环境变量
文章目录 查看电脑系统下载及安装JavaSE配置系统环境变量测试环境变量配置是否成功。 查看电脑系统 运行输入框中输入:control 下载及安装JavaSE 这个从网上下载就行,jdk-8u141-windows-x64.exe,不提供下载方式了。 主要讲解安装过程&a…...

保护移动设备免受恶意软件侵害优秀方法
几天前,移动恶意软件攻击增加了500%显然,我们大多数人都不知道不能很好地保护我们的手机下面小编揭秘有效保护移动设备免受恶意软件侵害的最佳方法。 1、使用移动反恶意软件 恶意软件很容易感染智能手机和平板电脑,因此在设备上安装可靠的…...
一个人在家怎么赚钱?普通人如何通过网络实现在家就能赚钱
近年来,随着互联网的飞速发展,嗅觉敏锐的人只要使用互联网就可以快乐地赚钱。一般来说,网上赚钱的投资较少,有时有一台能上网的电脑或手机就够了,所以大家有时称其为“无成本或低成本网赚”。今天就分享一个人在家如何…...
ChatGPT诞生的新岗位:提示工程师(Prompt Engineer)
ChatGPT诞生的新岗位:提示工程师(Prompt Engineer) Prompt 工程师是什么? 是识别人工智能的错误和隐藏功能,以便开发者可以对这些发现进行处理。 如果你正在寻找科技领域最热门的工作,你可以尝试了解如何与AI聊天机…...

机器学习笔记 使用PPOCRLabel标注自己的OCR数据集
一、PPOCRLabel的安装 最简单的方式就是直接pip安装,如下命令。 pip install PPOCRLabel -i https://pypi.douban.com/simple/ 运行的时候,直接激活安装了PPOCRLabel的环境后,输入PPOCRLabel回车即可运行,不过PPOCRLabel依赖PyQt5,所以会要求安装PyQt5,按要求安装或者提前…...

【C++初阶】类和对象(二)
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C初阶 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C初阶】…...

深入探讨Java、Spring和Dubbo的SPI机制
在Java开发领域中,SPI(Service Provider Interface)是一种用于实现框架扩展的机制。Java本身提供了SPI机制,Spring和Dubbo也都有自己的SPI机制。本文将介绍Java、Spring、Dubbo三者SPI机制的原理和区别。 一、Java SPI机制 Java…...
使用机器人为无线传感器网络提供服务(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 无线传感器网络是一种无线网络,包括大量循环的、自定向的、微小的、低功耗的设备,称为传感器节点&…...

QT自制软键盘 最完美、最简单、跟自带虚拟键盘一样
QT自制软键盘 最完美、最简单、跟自带虚拟键盘一样 [1] QT自制软键盘 最完美、最简单、跟自带虚拟键盘一样一、本自制虚拟键盘特点二、windows打开系统自带软键盘三、让键盘界面保持在最上方、不改变底层界面焦点四、长按按键重复输入键盘内容五、模拟键盘点击事件完成虚拟键盘…...

优思学院|8D和DMAIC两种方法应如何选择?
在现代的商业环境中,客户投诉是一个非常常见的问题。当客户不满意产品或服务时,他们往往会向企业发出投诉。质量管理部门是一个负责处理这些投诉的重要部门,因为它们需要确保产品和服务的质量满足客户的期望。改善方法是质量管理部门用来解决…...

回归预测 | MATLAB实现MLR多元线性回归预测(多指标评价)
回归预测 | MATLAB实现MLR多元线性回归预测(多指标评价) 目录 回归预测 | MATLAB实现MLR多元线性回归预测(多指标评价)预测效果基本介绍模型描述程序设计参考资料预测效果 基本介绍 回归预测 | MATLAB实现MLR多元线性回归预测(多指标评价) 模型描述 多元线性回归(Multip…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
