Problem E. 矩阵游戏 (2023年ccpc河南省赛)
原题链接:
https://codeforces.com/gym/104354
题意:
有一个n*m的矩阵,只有三种字符:0,1和?。从[1,1]走到[n,m],每次只能向下走或者向下走。当走到1的时候得一分,走到0的时候不得分,走到?的时候可以将他变为1从而得到一分,或者不变,求所有从[1,1]走到[n,m]的路径的得分的最大值
思路:
f[i][j][k]表示走到[i,j]恰好有k个?变成1的方案数的最大得分
状态转移:
a[i][j]‘0’:f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k])
a[i][j]‘1’:f[i][j][k]=max(f[i-1][j][k]+1,f[i][j-1][k]+1)
a[i][j]==‘?’:
改:f[i][j][k]=max(f[i-1][j][k-1]+1,f[i][j-1][k-1]+1)
不改:f[i][j][k]=max(f[i-1][j][k],f[i][j-1][k])
那么这样的空间复杂度是n* m * x,会mle
于是考虑将数组优化到二维:f[j][k]
1.将k从大到小枚举
在转移的时候,如果按正常枚举,就会出现重复的情况,这时候只需要将k从大到小进行枚举,就避免了重复
#include<bits/stdc++.h>
using namespace std;
int n,m,x;
int f[505][1005];
char a[505][505];
bool cheek(int x,int y){if(x>=1&&x<=n&&y>=1&&y<=m) return true;else return false;
}
void sove(){scanf("%d%d%d",&n,&m,&x);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int j=0;j<=m;j++){for(int k=0;k<=x;k++){f[j][k]=-0x3f3f3f3f;}}if(a[1][1]=='1'){f[1][0]=1;}else if(a[1][1]=='0'){f[1][0]=0;}else{f[1][1]=1;f[1][0]=0;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int k=x;k>=0;k--){if(a[i][j]=='1'){if(cheek(i-1,j)){f[j][k]=max(f[j][k],f[j][k]+1);}if(cheek(i,j-1)){f[j][k]=max(f[j][k],f[j-1][k]+1);}}else if(a[i][j]=='0'){if(cheek(i,j-1)){f[j][k]=max(f[j][k],f[j-1][k]);} }else{if(cheek(i-1,j)){if(k-1>=0) f[j][k]=max(f[j][k],f[j][k-1]+1);}if(cheek(i,j-1)){f[j][k]=max(f[j-1][k],f[j][k]);if(k-1>=0)f[j][k]=max(f[j][k],f[j-1][k-1]+1);} }}}}int ans=0;for(int i=0;i<=x;i++){ans=max(ans,f[m][i]);}cout<<ans<<endl;
}
int main(){int t;scanf("%d",&t);while(t--){sove();}return 0;
}
2.滚动数组
在转移的时候只用到了i和i-1层,那么我们就将i这一维开两个,在转移的时候在两维之间相互转移就可以了
#include<bits/stdc++.h>
using namespace std;
int n,m,x;
int f[3][505][1005];
char a[505][505];
bool cheek(int x,int y){if(x>=1&&x<=n&&y>=1&&y<=m) return true;else return false;
}
void sove(){scanf("%d%d%d",&n,&m,&x);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int i=0;i<3;i++){for(int j=0;j<=m;j++){for(int k=0;k<=x;k++){f[i][j][k]=-0x3f3f3f3f;}}
}if(a[1][1]=='1'){f[1][1][0]=1;}else if(a[1][1]=='0'){f[1][1][0]=0;}else{f[1][1][1]=1;f[1][1][0]=0;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int k=0;k<=x;k++){if(a[i][j]=='1'){if(cheek(i-1,j)){f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][j][k]+1);}if(cheek(i,j-1)){f[i&1][j][k]=max(f[i&1][j][k],f[i&1][j-1][k]+1);}}else if(a[i][j]=='0'){if(cheek(i-1,j)){f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][j][k]);}if(cheek(i,j-1)){f[i&1][j][k]=max(f[i&1][j][k],f[i&1][j-1][k]);} }else{if(cheek(i-1,j)){f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][j][k]);if(k-1>=0)f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][j][k-1]+1);}if(cheek(i,j-1)){f[i&1][j][k]=max(f[i&1][j][k],f[i&1][j-1][k]);if(k-1>=0)f[i&1][j][k]=max(f[i&1][j][k],f[i&1][j-1][k-1]+1);} }}}}int ans=0;for(int i=0;i<=x;i++){ans=max(ans,f[n&1][m][i]);} cout<<ans<<endl;
}
int main(){int t;scanf("%d",&t);while(t--){sove();}return 0;
}相关文章:
)
Problem E. 矩阵游戏 (2023年ccpc河南省赛)
原题链接: https://codeforces.com/gym/104354 题意: 有一个n*m的矩阵,只有三种字符:0,1和?。从[1,1]走到[n,m],每次只能向下走或者向下走。当走到1的时候得一分,走到0的时候不得分,走到?的时候可以将他…...
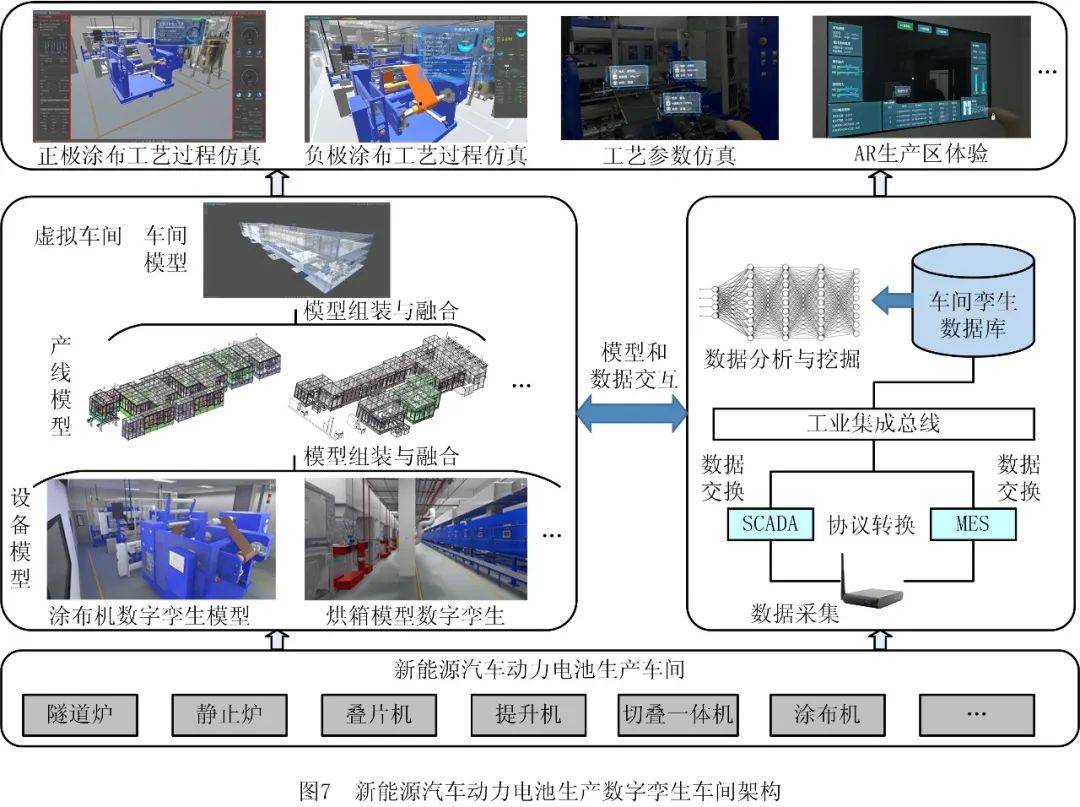
数字孪生模型构建理论及应用
源自:计算机集成制造系统 作者:陶飞 张贺 戚庆林 徐 俊 孙铮 胡天亮 刘晓军 刘庭煜 关俊涛 陈畅宇 孟凡伟 张辰源 李志远 魏永利 朱铭浩 肖斌 摘 要 数字孪生作为实现数字化转型和促进智能化升级的重要使能途径,一直备受各…...

Vue面试题:30道含答案和代码示例的练习题
Vue中的双向数据绑定是怎么实现的? 双向数据绑定通过使用v-model指令实现。v-model指令会在表单元素上创建一个监听器,在用户输入时实时更新Vue实例的数据,并且在Vue实例数据变化时更新表单元素的值。 如何在Vue中定义一个方法?…...
)
2023-05-09 LeetCode每日一题(有效时间的数目)
2023-05-09每日一题 一、题目编号 2437. 有效时间的数目二、题目链接 点击跳转到题目位置 三、题目描述 给你一个长度为 5 的字符串 time ,表示一个电子时钟当前的时间,格式为 “hh:mm” 。最早 可能的时间是 “00:00” ,最晚 可能的时间…...
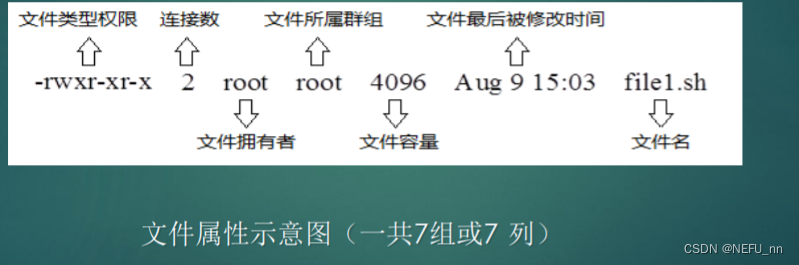
第三节课 Linux文件权限
目录 文件属性详解 权限修改 文件所有者与属组修改 文件默认权限修改 Linux是多人多任务的操作系统,因此可能常常会有多人使用一台机器, 为了考虑每个人的隐私、方便用户合作,每个文件都有三类用户,权限是基于这三类用户设定的…...

开发STC89C51系列单片机需要的单片机技术
端口操作:控制单片机的输入输出端口,与外界进行通信。中断优先级:当多个中断同时发生时,确定哪个中断优先级更高,优先响应。时钟模块:控制单片机的时钟,可以精确计时。PWM技术:实现模…...
)
分布式键值存储是什么?(分布式键值存储大值)
文章目录 什么是分布式键值存储?分布式键值存储“大值”指什么? 什么是分布式键值存储? 分布式键值存储是一种分布式数据存储系统,它将数据存储为键值对的形式,并将这些键值对分散在多个节点上。每个节点都可以独立地…...
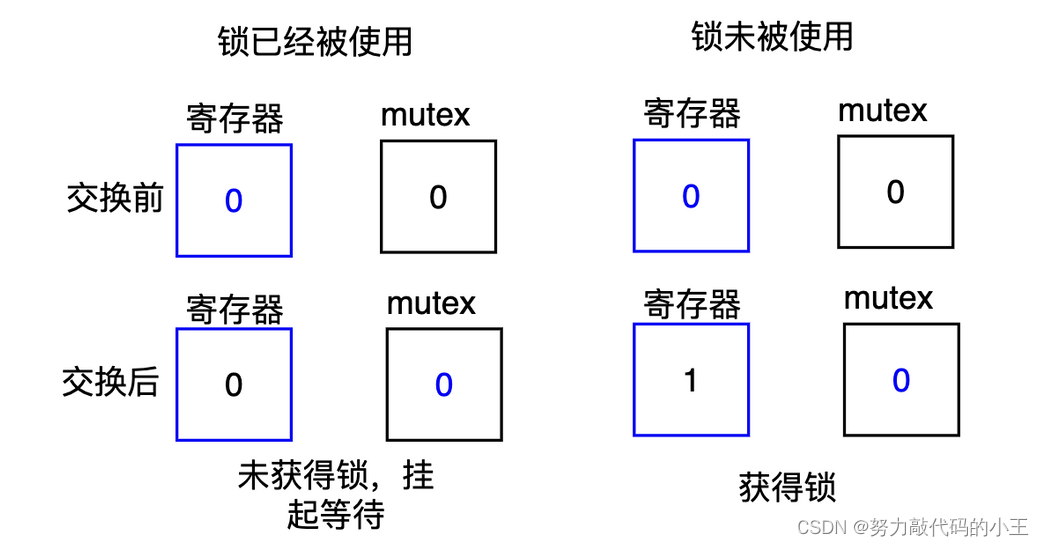
多线程(线程同步和互斥+线程安全+条件变量)
线程互斥 线程互斥: 任何时刻,保证只有一个执行流进入临界区访问临界资源,通常对临界资源起到保护作用 相关概念 临界资源: 一次仅允许一个进程使用的共享资源临界区: 每个线程内部,访问临界资源的代码&am…...

Flutter学习——开发Flutter需要的技能
第二章 Flutter开发所需要掌握的知识 文章目录 第二章 Flutter开发所需要掌握的知识前言一、开发语言Dart语言Android/Ios知识 二、组件学习三、调试与性能优化总结 前言 上一章,介绍了Flutter的来源和平台支持及特点,这一章,来梳理一下学习…...
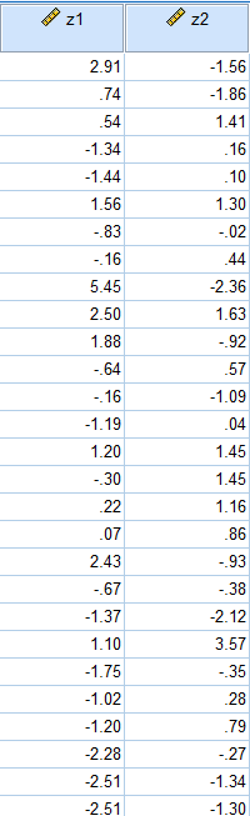
SPSS如何进行因子分析和主成分分析之案例实训?
文章目录 0.引言1.因子分析2.主成分分析 0.引言 因科研等多场景需要进行数据统计分析,笔者对SPSS进行了学习,本文通过《SPSS统计分析从入门到精通》及其配套素材结合网上相关资料进行学习笔记总结,本文对因子分析和主成分分析进行阐述。 1.因…...

图标字体与HTML转义字符:网页设计中的两个关键概念
在网页设计中,图标字体和HTML转义字符是两个重要的概念。图标字体用于显示网页的图标,可以让用户更加直观地理解网页的内容。而HTML转义字符则用于在网页中插入特殊的字符,以保证网页的安全性和可读性。 一、图标字体 在网页中显示图标&#…...
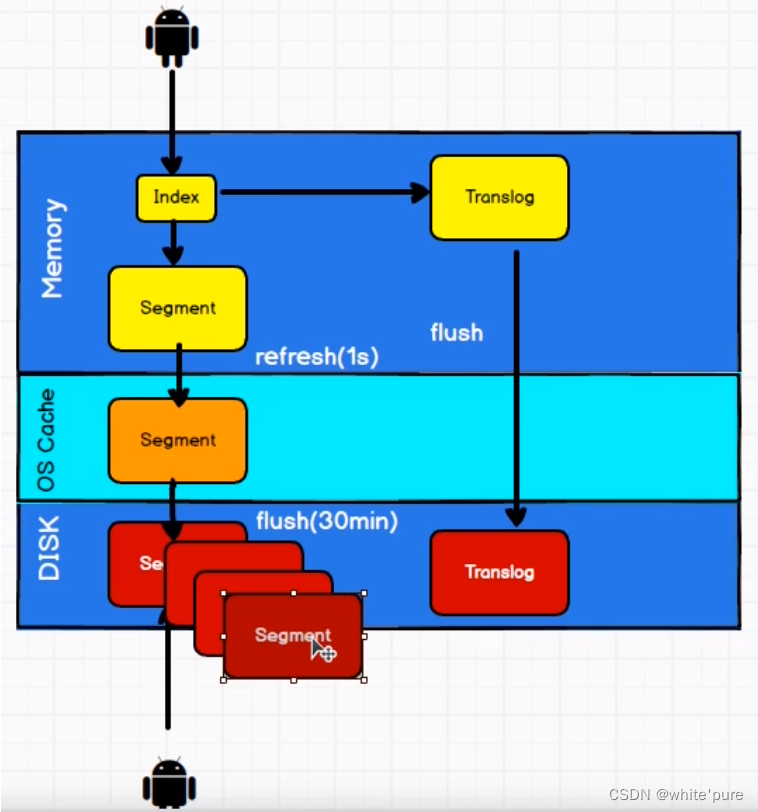
Elasticsearch详解
文章目录 概览使用与ES交互索引创建索引查询索引删除文档创建修改文档局部修改文档查询文档删除全查询 整合SpringBootpom依赖application.ymlElasticsearchAutoConfigurationElasticsearchPropertiesElasticsearchConstantPersonSearchPageHelperPersonServiceBaseElasticsear…...
网络基础)
学习笔记(13)网络基础
目录 1,get与post的区别2,JSON解析2.1,JSON.stringify2.2,JSON.parse 3,cookie3.1,set方法3.2,cookie方法用于设置响应头, 4,http模块4.1,请求报文和响应报文…...

LeertCode 134 加油站
题目: 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。给定两个整数数组 …...

python文件操作的基本流程
引入 程序运行过程中产生的数据会保存到内存中,如果想要永久保存下来,就必须将数据存放在硬盘上,应用程序如果想要操作计算机的硬件就必须通过操作系统,文件就是操作系统提供给应用程序来操作硬盘的虚拟概念,应用程序…...
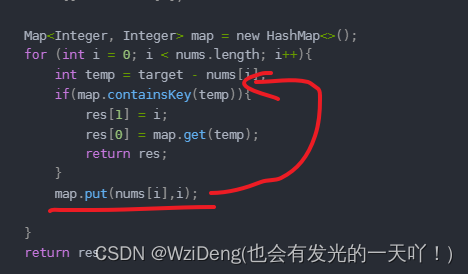
1. 两数之和
原题链接: 1. 两数之和 https://leetcode.cn/problems/two-sum/ 完成情况: ##1. n 2 n^2 n2复杂度 2.HashMap进行优化 3.空间换时间方法 即,构建一个 1 0 − 9 10^-9 10−9 到 1 0 9 10^9 109这个大的数组,然后把数填进去&…...

操作系统:06 进程通信
1 基本概念 进程间通信是指两个或多个进程之间交互数据的过程,因为进程之间是相互独立的,为了协同工作必须进行进程间交互数据 2 进程间通信的分类 2.1 简单的进程间通信: 信号(携带附加数据)、文件、命令行参数、环境变量表 2.2 传统的进…...

WRF模式
随着生态文明建设和“碳中和”战略的持续推进,我国及全球气候变化及应对是政府、科学界及商业界关注的焦点。气候是多个领域(生态、水资源、风资源及碳中和等问题)的主要驱动因素,合理认知气候变化有利于解释生态环境变化机理及过…...
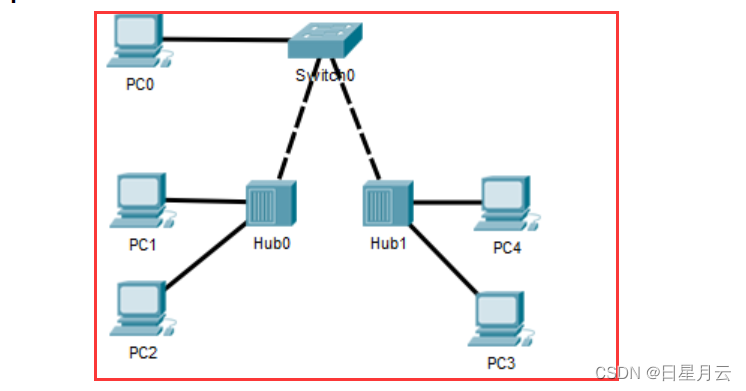
2直接连接的网络与VLAN划分【实验】【计算机网络】
2直接连接的网络与VLAN划分【实验】【计算机网络】 前言推荐2直接连接的网络与VLAN划分2.1共享式以太网和交换式以太网实验目的实验内容及实验环境实验原理共享式以太网交换式以太网 实验过程搭建实验环境初始化序训练操作共享式以太网-操作交换式以太网查看共享式以太网冲突查…...

【Linux0.11代码分析】04 之 head.s 启动流程
【Linux0.11代码分析】04 之 head.s 启动流程 一、boot/head.s 系列文章如下: 系列文章汇总:《【Linux0.11代码分析】之 系列文章链接汇总(全)》 . 1.《【Linux0.11代码分析】01 之 代码目录分析》 2.《【Linux0.11代码分析】02 之…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
