前端:20 个常见的前端算法题
现在面试中,算法出现的频率越来越高了,大厂基本必考
今天给大家带来 20 个常见的前端算法题,重要的地方已添加注释,如有不正确的地方,欢迎多多指正 💕
1、两数之和
题目: 给定一个数组 nums 和一个目标值 target,在该数组中找出和为目标值的两个数
输入: nums: [8, 2, 6, 5, 4, 1, 3] ; target:7
输出: [2, 5]
// 时间复杂度O(n)、 空间复杂度O(n)
function twoNumAdd(arr, target) {if (Array.isArray(arr)) {// 使用map将遍历过的数字存起来,空间换时间let map = {};for (let i = 0; i < arr.length; i++) {// 从map中查找是否有key 等于 target-nums[i],如果有,则条件成立,返回结果if (map[target - arr[i]] !== undefined) {return [target - arr[i], arr[i]];} else {// 条件不成立,将该值存起来map[arr[i]] = i;}}}return [];
}
2、三数之和
题目: 给定一个数组 nums,判断 nums 中是否存在三个元素a,b,c,使得 a + b + c = target,找出所有满足条件且不重复的三元组合
输入: nums: [5, 2, 1, 1, 3, 4, 6] ;target:8
输出: [[1, 1, 6], [1, 2, 5], [1, 3, 4]]
// 用`双端指针`的方式,将三数之和转化为两数之和
function findThree(arr, target) {// 先将数组从小到大排序arr.sort();let result = [];for (let i = 0; i < arr.length; i++) {// 跳过重复的arr[i]值, 比如[2, 1, 1],跳过第二个1if (i && arr[i] === arr[i - 1]) continue;let left = i + 1;let right = arr.length - 1;// 双端指针left、rightwhile (left < right) {let sum = arr[i] + arr[left] + arr[right];if (sum > target) {right--;} else if (sum < target) {left++;} else {// 先取arr[left],然后left++, 两步合成一步;arr[right--]同样的逻辑result.push([arr[i], arr[left++], arr[right--]]);while (arr[left] === arr[left - 1]) {// 跳过重复的arr[left]值,left++;}while (arr[right] === arr[right + 1]) {// 跳过重复的arr[right]值right--;}}}}return result;
}
3、版本号排序
题目: 输入一组版本号,输出从大到小的排序
输入: [‘2.1.2’, ‘0.402.1’, ‘3.20.1’, ‘0.1.8’, ‘5.1.2’, ‘1.3.4.5’]
输出: [‘5.1.2’, ‘3.20.1’, ‘2.1.2’, ‘1.3.4.5’, ‘0.402.1’, ‘0.1.8’]
function versionSort(arr) {return arr.sort((a, b) => {let i = 0;const arr1 = a.split(".");const arr2 = b.split(".");while (true) {// 取出相同位置的数字const s1 = arr1[i];const s2 = arr2[i];i++;// 若s1 或 s2 不存在,说明相同的位置已比较完成,接下来比较arr1 与 arr2的长度,长的版本号大if (s1 === undefined || s2 === undefined) {return arr2.length - arr1.length;}if (s1 === s2) continue;// 比较相同位置的数字大小return s2 - s1;}});
}
4、第一个不重复的字符
题目: 输入一个字符串,找到第一个不重复字符的下标
输入: ‘abcabcde’
输出: 6
// 时间复杂度O(n)、 空间复杂度O(n)
function findOneStr(str) {if (!str) return -1;// 使用map存储每个字符出现的次数let map = {};let arr = str.split("");arr.forEach(item => {let val = map[item];// val为undefined时,表示未存储,map[item] = 1;否则map[item] = val + 1map[item] = val ? val + 1 : 1;});// 再遍历一遍找到出现1次的下标for (let i = 0; i < arr.length; i++) {if (map[arr[i]] == 1) {return i;}}return -1;
}
5、字符串所有排列组合
题目: 输入一个字符串,打印出该字符串中,所有字符的排列组合
输入: ‘abc’
输出: [‘abc’, ‘acb’, ‘bca’, ‘bac’, ‘cab’, ‘cba’]
/*** 利用回溯算法,计算所有字符串的组合* @param {array} list - 字符串列表* @param {array} result - 最终的结果* @param {string} current - 当前的字符串* @param {string} temp - 当前固定的字符
*/
function stringGroup(list = [], result = [], current = "", temp = "") {current += temp;if (list.length === 0) {// 递归的出口,将对应结果添加到list中return result.push(current);}for (let i = 0; i < list.length; i++) {// 每次递归 固定第一个字符temp = list.shift();stringGroup(list, result, current, temp);// 将删除的temp重新添加到queue尾部,实现将数组反转的效果,如[a,b,c]反转为[c,b,a]list.push(temp);}// 这里去重是解决str中有重复的字母,比如str为'aacd'return [...new Set(result)];
}
6、冒泡排序
时间复杂度为O(n²),稳定排序算法
function bubbleSort(arr) {let length = arr.length;// 外层循环用控制 排序进行多少轮for (let i = 0; i < length; i++) {// 内层循环用于每一轮的数据比较// 注意j的长度范围 length - i - 1for (let j = 0; j < length - i - 1; j++) {// 相邻元素,大的放到后面if (arr[j] > arr[j + 1]) {// 交换位置[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];}}}return arr;
}
7、选择排序
时间复杂度为O(n²),不稳定
function selectSort(arr) {// 定义index存储最小值的下标let index;// 外层循环用控制 排序进行多少轮for (let i = 0; i < arr.length - 1; i++) {index = i;// 内层循环用于每一轮的数据比较// 注意j的起始范围是 i + 1for (let j = i + 1; j < arr.length; j++) {// 寻找最小值if (arr[j] < arr[index]) {// 保存最小值的下标index = j;}}// 如果 index 不是目前的头部元素,则交换两者if (index !== i) {[arr[i], arr[index]] = [arr[index], arr[i]];}}return arr;
}
8、插入排序
时间复杂度为O(n²),稳定
function insertSort(arr) {// 从第 2 个元素开始遍历序列for (let i = 1; i < arr.length; i++) {let j = i;//记录要插入的目标元素let target = arr[j];//从 target 所在位置向前遍历,直至找到一个比目标元素小的元素,目标元素插入到该元素之后的位置while (j > 0 && arr[j - 1] > target) {//移动前一个元素的位置,将其向后移动一个位置arr[j] = arr[j - 1];j--;}arr[j] = target;}return arr;
}
9、快速排序
时间复杂度为O(nlogn),不稳定
function quickSort(list) {// 当list.length <= 1时,退出递归if (list.length <= 1) return list;// 找到中间节点let mid = Math.floor(list.length / 2);// 以中间节点为基准点,比该节点大的值放到right数组中,否则放到left数组中let base = list.splice(mid, 1)[0];let left = [];let right = [];list.forEach(item => {if (item > base) {right.push(item);} else {left.push(item);}});// 重新组合数组return quickSort(left).concat(base, quickSort(right));
}
10、归并排序
时间复杂度为O(nlogn),稳定
function MergeSort(array) {let len = array.length;// 当每个子序列中仅有1个元素时返回if (len <= 1) {return array;}// 将给定的列表分为两半let num = Math.floor(len / 2);let left = MergeSort(array.slice(0, num));let right = MergeSort(array.slice(num, array.length));return merge(left, right);function merge(left, right) {let [l, r] = [0, 0];let result = [];// 从 left 和 right 区域中各个取出第一个元素,比较它们的大小while (l < left.length && r < right.length) {// 将较小的元素添加到result中,然后从较小元素所在的区域内取出下一个元素,继续进行比较;if (left[l] < right[r]) {result.push(left[l]);l++;} else {result.push(right[r]);r++;}}// 如果 left 或者 right 有一方为空,则直接将另一方的所有元素依次添加到result中result = result.concat(left.slice(l, left.length));result = result.concat(right.slice(r, right.length));return result;}
}
11、列表转成树
题目: 输入一组列表如下,转化成树形结构
输入:
[{ id: 1, title: "child1", parentId: 0 },{ id: 2, title: "child2", parentId: 0 },{ id: 3, title: "child1_1", parentId: 1 },{ id: 4, title: "child1_2", parentId: 1 },{ id: 5, title: "child2_1", parentId: 2 }
]
输出:
tree=[{"id": 1,"title": "child1","parentId": 0,"children": [{"id": 3,"title": "child1_1","parentId": 1},{"id": 4,"title": "child1_2","parentId": 1}]},{"id": 2,"title": "child2","parentId": 0,"children": [{"id": 5,"title": "child2_1","parentId": 2}]}
]
function listToTree(data) {// 使用对象重新存储数据, 空间换时间let map = {};// treeData存储最后结果let treeData = [];// 遍历原始数据data,存到map中,id为key,值为数据for (let i = 0; i < data.length; i++) {map[data[i].id] = data[i];}// 遍历对象for (let i in map) {// 根据 parentId 找到的是父节点if (map[i].parentId) {if (!map[map[i].parentId].children) {map[map[i].parentId].children = [];}// 将子节点放到父节点的 children中map[map[i].parentId].children.push(map[i]);} else {// parentId 找不到对应值,说明是根结点,直接插到根数组中treeData.push(map[i]);}}return treeData;
}
12、深度优先遍历
题目: 对树进行遍历,从第一个节点开始,遍历其子节点,直到它的所有子节点都被遍历完毕,然后再遍历它的兄弟节点
输入: 上文第 11 题生成的 tree
输出: [1, 3, 4, 2, 5]
// 递归版本
function deepTree(tree, arr = []) {if (!tree || !tree.length) return arr;tree.forEach(data => {arr.push(data.id);// 遍历子树data.children && deepTree(data.children, arr);});return arr;
}// 非递归版本
function deepTree(tree) {if (!tree || !tree.length) return;let arr = [];let stack = [];//先将第一层节点放入栈for (let i = 0, len = tree.length; i < len; i++) {stack.push(tree[i]);}let node;while (stack.length) {// 获取当前第一个节点node = stack.shift();arr.push(node.id);//如果该节点有子节点,继续添加进入栈顶if (node.children && node.children.length) {stack = node.children.concat(stack);}}return arr;
}
13、广度优先遍历
题目: 以横向的维度对树进行遍历,从第一个节点开始,依次遍历其所有的兄弟节点,再遍历第一个节点的子节点,一层层向下遍历
输入: 上文第 11 题生成的 tree
输出: [1, 2, 3, 4, 5]
function rangeTree(tree) {if (!tree || !tree.length) return;let arr = [];let node, list = [...tree];// 取出当前节点while ((node = list.shift())) {arr.push(node.id);node.children && list.push(...node.children);}return arr;
}
14、树形结构查找节点
题目: 查找树形结构中符合要求的节点
输入:
tree: 上文第 11 题生成的 tree
func: data => data.title === “child2_1”
输出:{ id: 5, parentId: 2, title: “child2_1” }
/**
* 查找节点
* @param {array} tree - 树
* @param {function} func - 查找条件
* */
function findTreeNode(tree, func) {for (const data of tree) {// 条件成立 直接返回if (func(data)) return data;if (data.children) {const res = findTreeNode(data.children, func);// 结果存在再返回if (res) return res;}}return null;
}
// 测试
findTreeNode(tree, data => data.title === "child2_1")
15、二叉查找树
题目: 判断一个数组,是否为某二叉查找树的前序遍历结果,二叉查找树特点是所有的左节点比父节点的值小,所有的右节点比父节点的值大
输入: [5, 3, 2, 1, 4, 6, 7, 8, 9]
输出: true
function preOrderOfBST(list) {if (list && list.length > 0) {// 前序遍历,第一个值为根节点var root = list[0];// 找到数组中,第一个比根节点大的节点,即为右子树的节点for (var i = 0; i < list.length; i++) {if (list[i] > root) {break;}}// 遍历右子树的节点,要求所有右子树的节点都比根节点大for (let j = i; j < list.length; j++) {if (list[j] < root) {return false;}}var left = true;// 同理,递归判断左子树是否符合二叉查找树的规则if (i > 1) {left = preOrderOfBST(list.slice(1, i + 1));}var right = true;// 递归判断右子树是否符合二叉查找树的规则if (i < list.length) {right = preOrderOfBST(list.slice(i, list.length));}// 左、右子树都符合要求,则是一个二叉查找树return left && right;}
}
16、查找二叉树的路径
题目: 查找二叉树和为某一值的路径
输入: 二叉树结构如下,找到和为 11 的所有路径
输出: [[5, 3, 2, 1], [5, 6]]
/**
* 利用回溯算法,找到和为某一值的路径
* @param {object} node - 二叉树
* @param {number} num - 目标值
* @param {array} stack - 栈
* @param {number} sum - 当前路径的和
* @param {array} result - 存储所有的结果
* */
function findPath(node, num, stack = [], sum = 0, result = []) {stack.push(node.data);sum += node.data;// 找到所有的节点路径(包含叶子节点和子节点的所有情况之和)if (sum === num) {// if (!node.left && !node.right && sum === num) { // 找到所有的叶子节点路径result.push(stack.slice());}if (node.left) {findPath(node.left, num, stack, sum, result);}if (node.right) {findPath(node.right, num, stack, sum, result);}// 回溯算法:不符合要求,退回来,换一条路再试// 叶子节点直接pop;子节点中的所有的节点递归完成后再popstack.pop();return result;
}
17、买卖股票问题
题目: 给定一个整数数组,其中第 i 个元素代表了第 i天的股票价格;
非负整数 fee 代表了交易股票的手续费用,求返回获得利润的最大值
输入: arr: [1, 12, 13, 9, 15, 8, 6, 16]; fee: 2
输出: 22
/*** 贪心算法求解* @param {array} list - 股票每天的价格列表* @param {number} fee - 手续费* */
function buyStock(list, fee) {// min为当前的最小值,即买入点let min = list[0],sum = 0;for (let i = 1; i < list.length; i++) {// 从1开始,依次判断if (list[i] < min) {// 寻找数组的最小值min = list[i];} else {// 计算如果当天卖出是否赚钱let temp = list[i] - min - fee;if (temp > 0) {// 赚钱 存数据sum += temp;// 关键代码:重新计算min,分两种情况,如果后面继续涨,则默认继续持有;若后面跌,则以后面的价格重新买入min = list[i] - fee;}}}return sum;
}
18、斐波那契数列
题目: 从第 3 项开始,当前项等于前两项之和: 1 1 2 3 5 8 13 21 ……,计算第 n 项的值
输入: 10
输出: 89
// 使用动态规划,将复杂的问题拆分,也就是:`F(N) = F(N - 1) + F(N - 2)`,用数组将已经计算过的值存起来
function fib(n) {// 使用dp数组,将之前计算的结果存起来,防止栈溢出if (n < 2) return 1;let dp = [1, 1];for (let i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}
19、滑动窗口最大值
题目: 给定一个数组 nums,有一个大小为 k 的滑动窗口,从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口中的 k 个数字。滑动窗口每次只向右移动一位,求返回滑动窗口最大值
输入: nums: [1,3,-1,-3,5,3,6,7]; k: 3
输出: [3, 3, 5, 5, 6, 7]
function maxSlidingWindow(nums, k) {// window存储当前窗口中数据的下标const window = [];// result存储窗口中的最大值const result = [];for (let i = 0; i < nums.length; i++) {if (i - window[0] > k - 1) {// 剔除窗口长度超出范围时左侧的最大值window.shift();}for (let j = window.length - 1; j >= 0; j--) {// 当前窗口的值依次和要插入的值做比较,如果小于要插入的值,剔除掉该值,直到window为空为止(保证window中最左侧的值为最大值)if (nums[window[j]] <= nums[i]) {window.pop();}}// 添加右侧新加入的值,插入新值时有两种情况:// 1、新值为最大值时,则window此时为空;// 2、新值不为最大值时,window已剔除掉比新值小的值window.push(i);if (i >= k - 1) {// 窗口是从0开始移动,当移动的距离大于等于目标范围后,以后再往后移动一次,就要写入当前窗口的最大值result.push(nums[window[0]]);}}return result;
}
20、最长递增子序列
题目: 一个整数数组 nums,找到其中一组最长递增子序列的值
输入: [3,5,7,1,2,8]
输出: [3,5,7,8]
function lengthOfLIS(nums) {if (!nums.length) return 0;// 创建一个和原数组等长的数组dp,用来存储每一项的最长递增子序列// 比如[1,2,2] 表示第二项和第三项的最长递增子序列都为2let dp = new Array(nums.length).fill(1);// 双层for循环,每一项都和之前的所有项一一进行比较,计算出该项的最长递增子序列个数,存储到dp中for (let i = 0; i < nums.length; i++) {// 当前项依次和之前的每一项进行比较,累加出当前项的最长递增子序列for (let j = 0; j < i; j++) {if (nums[j] < nums[i]) {// 比较当前项已有的最大值和之前项最大值,比如当比较到第三项[1,2,2]时,如第三项比第二项大,所以第三项的计算结果为[1,2,3]dp[i] = Math.max(dp[i], dp[j] + 1);}}}// 取出一组最长递增子序列的具体值(注意:最长递增子序列有可能有多组值,这里是只取出其中一组值)// 找到dp中的最大值,该值就是nums的最长递增子序列的个数let max = Math.max(...dp);let result = [];for (let i = max; i >= 1; i--) {// 倒序遍历,根据长度获取对应的值findArrNode(dp, i, result, nums);}return result;
}
function findArrNode(dp, value, result, arr) {// 找到符合条件最后一项的下标,这样才能保证数组的顺序是正确的let index = dp.lastIndexOf(value);// 存储对应的值result.unshift(arr[index]);// 对dp进行截取,保证只取最大项之前的数据dp.length = index + 1;
}
相关文章:

前端:20 个常见的前端算法题
现在面试中,算法出现的频率越来越高了,大厂基本必考 今天给大家带来 20 个常见的前端算法题,重要的地方已添加注释,如有不正确的地方,欢迎多多指正 💕 1、两数之和 题目: 给定一个数组 nums …...
【Linux】多线程 --- 线程概念 控制 封装
从前种种,譬如昨日死。从后种种,往如今日生。 文章目录 一、线程概念1.重新理解用户级页表1.1 进程资源如何进行分配呢?(地址空间页表)1.2 虚拟地址如何转换到物理地址?(页目录页表项࿰…...

最长递增子序列的长度 _ 贪心+二分查找 _ 20230510
最长递增子序列的长度 _ 贪心二分查找 _ 20230510 前言 最长递增子序列的程序一般采用动态规划方式,使用bottom-up的数组记忆方式比较容易理解,当然也可以采用top-down的递归模式。本文主要讨论如何利用贪心策略,同时辅助以二分查找的方式实…...

VMware ESXi 7.0 U3m Unlocker OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版)
ESXi 7 U3 标准版集成 Intel 网卡、USB 网卡 和 NVMe 驱动 请访问原文链接:https://sysin.org/blog/vmware-esxi-7-u3-sysin/,查看最新版。原创作品,转载请保留出处。 作者主页:sysin.org 2023-05-03,发布 ESXi 7.0U…...
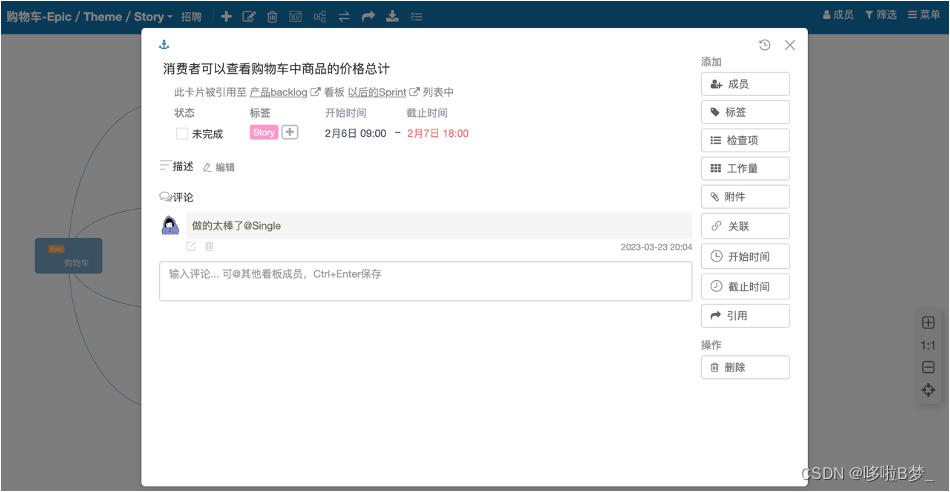
Scrum敏捷开发和项目管理流程及工具
Scrum是全球运用最广泛的敏捷管理框架,Leangoo基于Scrum框架提供了一系列的流程和模板,可以帮助敏捷团队快速启动Scrum敏捷开发。 这里可以介绍一下在scrum中单团队敏捷开发如何管理,单团队敏捷开发主要是针对10-15人以下,只有一…...

微服务之配置中心
文章目录 1什么是配置2什么是配置中心3为什么我们要用配置中心4特点 1什么是配置 就是springboot中的application.yml/properties文件 比如:项目名、端口号、数据库连接参数、启动参数等。 2什么是配置中心 配置中心就是用来管理项目当中所有配置的系统ÿ…...
windows下安装OpenCL
由于我的电脑是windows10,显卡是集显Intel UHD Graphics 630。 下载Intel的SDK for OpenCL,下载地址https://software.intel.com/en-us/opencl-sdk/choose-download,也可以在我的资源里面直接下载https://download.csdn.net/download/qq_363…...
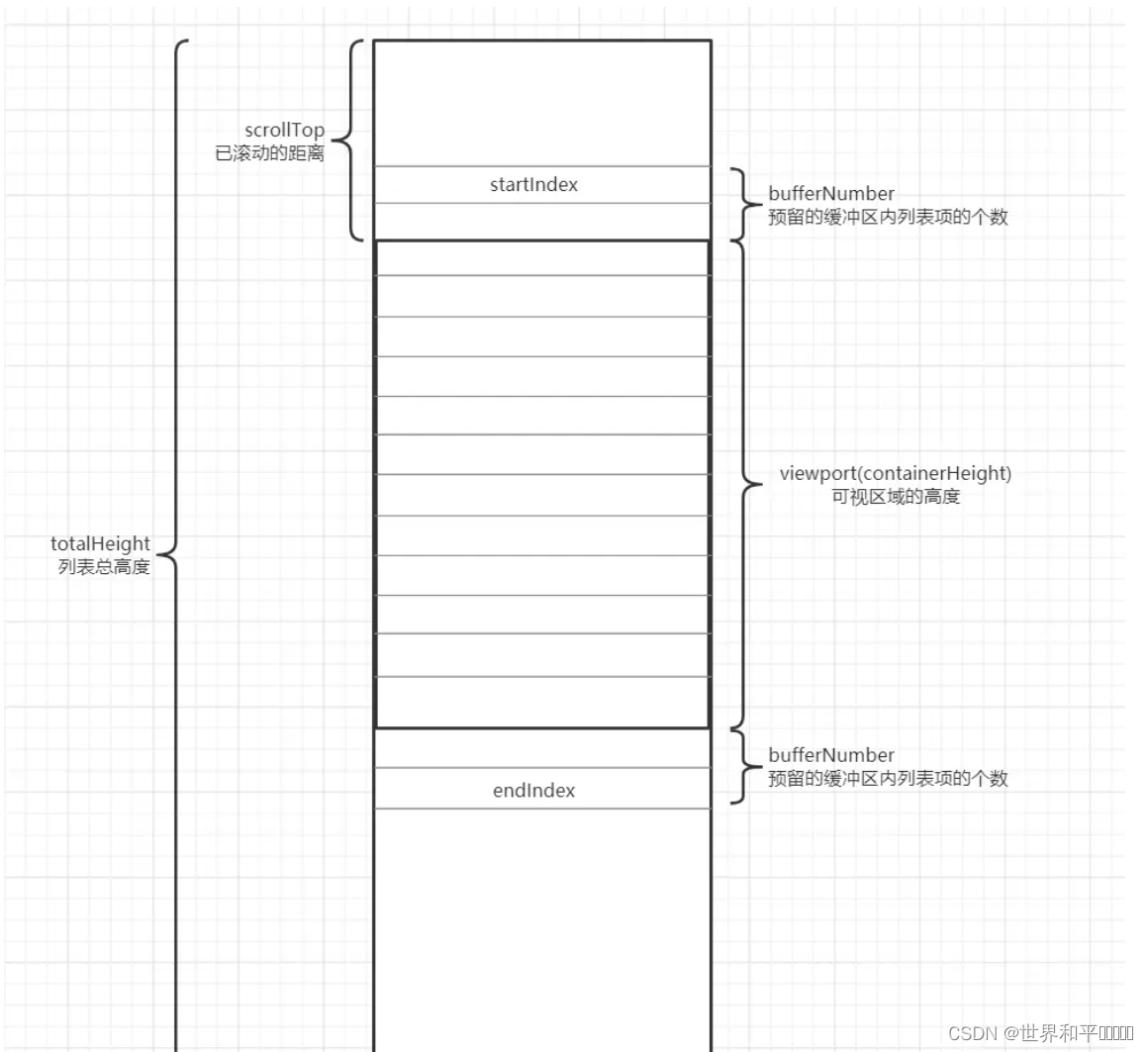
前端项目的通用优化策略
一、虚拟滚动 当我们开发的时候,遇到大数据加载,页面卡顿的问题应该如何处理?大多数情况下,我们都是尽量通过分页的方式处理这类问题,但是总有一些特殊的情况我们必须把数据全部加载到前端进行处理。我曾经遇到过一个…...
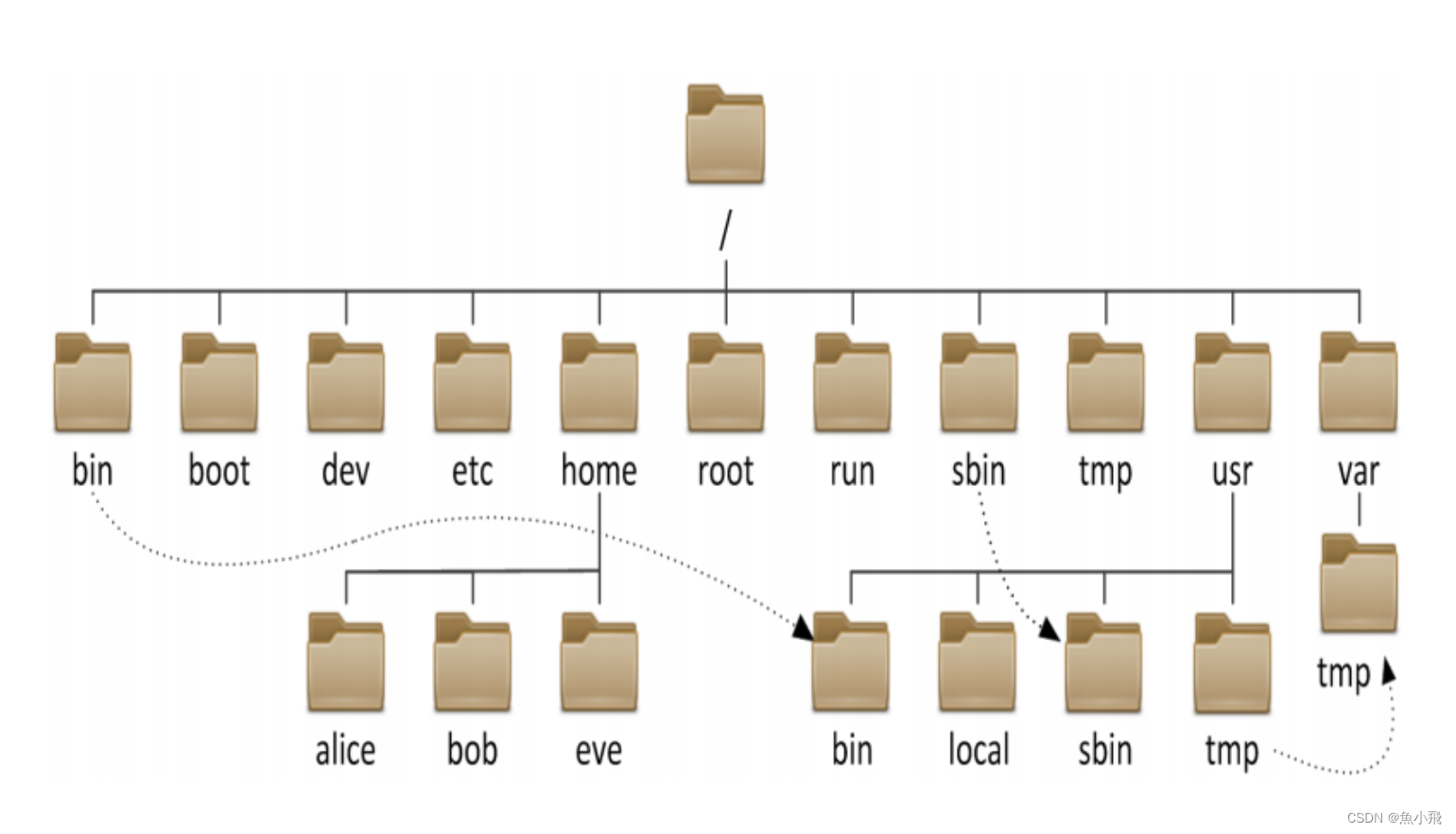
关于 IO、存储、硬盘和文件系统
关于IO、存储、硬盘和文件系统 0.引入1.了解IO1.1.存储器IO1.2.设备IO 2.存储介质和存储类型2.1.内存2.2.硬盘2.3.固态硬盘(SSD)2.4.U盘 3.硬盘的工作原理3.1.磁头3.2.盘片3.3.电动机3.4.硬盘的读写操作 4.文件系统概述4.1.文件系统的类型4.2.文件系统的…...

计算机网络期中复习提纲-酷酷的聪整理版
第一章 概述 1.请介绍计算机网络在逻辑上的组成及其各自的作用。 计算机网络在逻辑上可以分为终端子网和通信子网两部分。 终端子网是指连接计算机与网络的部分,主要负责将数据从计算机发送到通信子网,或将从通信子网接收到的数据传输到计算机。终端子网通常包括物理层和数据…...
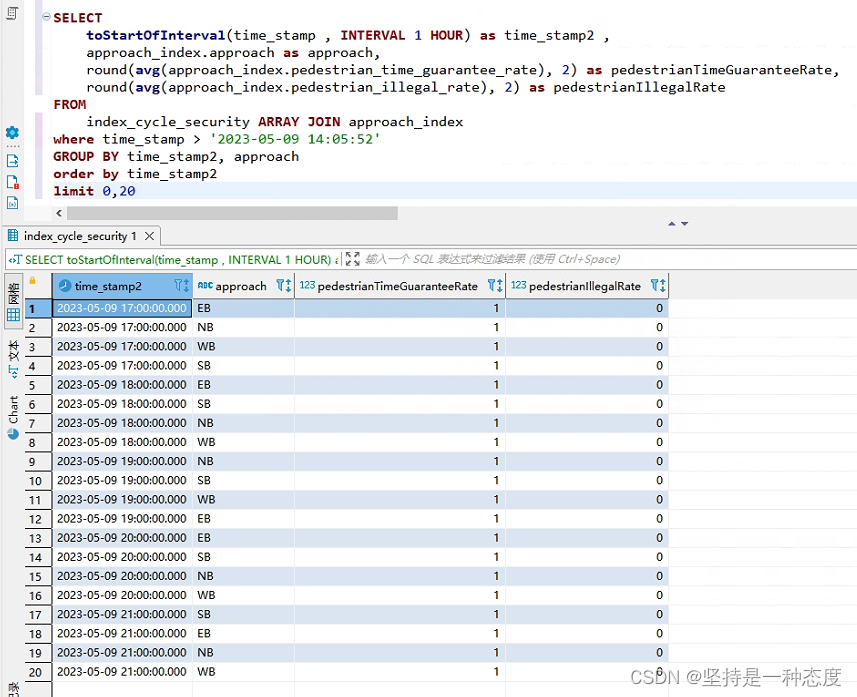
clickhouse的嵌套数据结构Tuple、Array与Nested类型介绍和使用示例
文章目录 Tuple类型Array类型Nested类型使用示例单独使用Tuple数组嵌套 Array(Tuple)Nested类型 生产使用:分组查询 Tuple类型 Tuple是ClickHouse数据库中的一种数据类型,它允许在一个字段中存储由不同数据类型组成的元组(tuple)。元组可以包含任意数量…...

人脸修复增强调研
Real-ESRGAN 工程地址:https://github.com/xinntao/Real-ESRGAN 效果: 人脸增强部分,调用的GFPGAN. GFPGAN 工程地址:https://github.com/TencentARC/GFPGAN 论文效果: BasicSR-ESRGAN: 项目地址&a…...
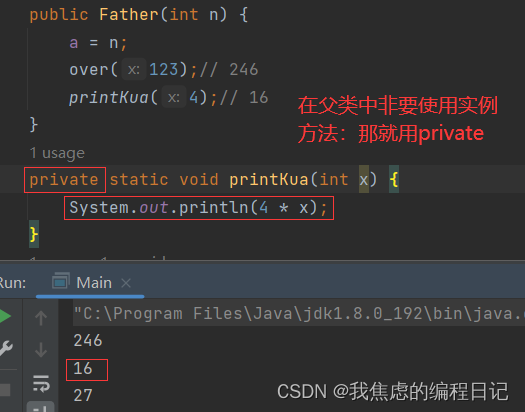
【Java】继承和多态
文章目录 一、继承1.继承的例子(is-a)2.组合的例子(has-a) 二、多态1.重写2.重载 三、继承的语法四、继承的注意事项1.初始化的顺序:2.super关键字 五、继承访问限定符六、多态实现方式七、多态的理解注意事项…...

ThingsBoard集群部署之k8s
1、概述 今天终于有时间去搞这个啦,拖了很久了,一直没时间,因为我本地没有那么多机器资源,开虚拟机不够,如果租用阿里云服务器,需要有充值的时间,因为这个费用是按小时付费,需要有连贯的时间来搞才行,今天恰好有时间,就开始搞了,弄成功搞出来了,特地写博客记录下来…...

【Gorm】如何在 GORM 中实现模型之间的关联?
文章目录 关联1、Belongs To(属于)2、Has One(拥有一个)3、Has Many(拥有多个)4、Many To Many(多对多) 关联 当涉及到 ORM(Object-Relational Mapping)的…...

Linux危险命令
rm -rf 命令 该命令可能导致不可恢复的系统崩坏。 rm -rf / #强制删除根目录下所有东西。rm -rf * #强制删除当前目录的所有文件。rm -rf . #强制删除当前文件夹及其子文件夹。fork 炸弹 :() { :|:& };:不太好理解可以转换成 bomb() {bomb|bomb& }; bomb一旦执行…...
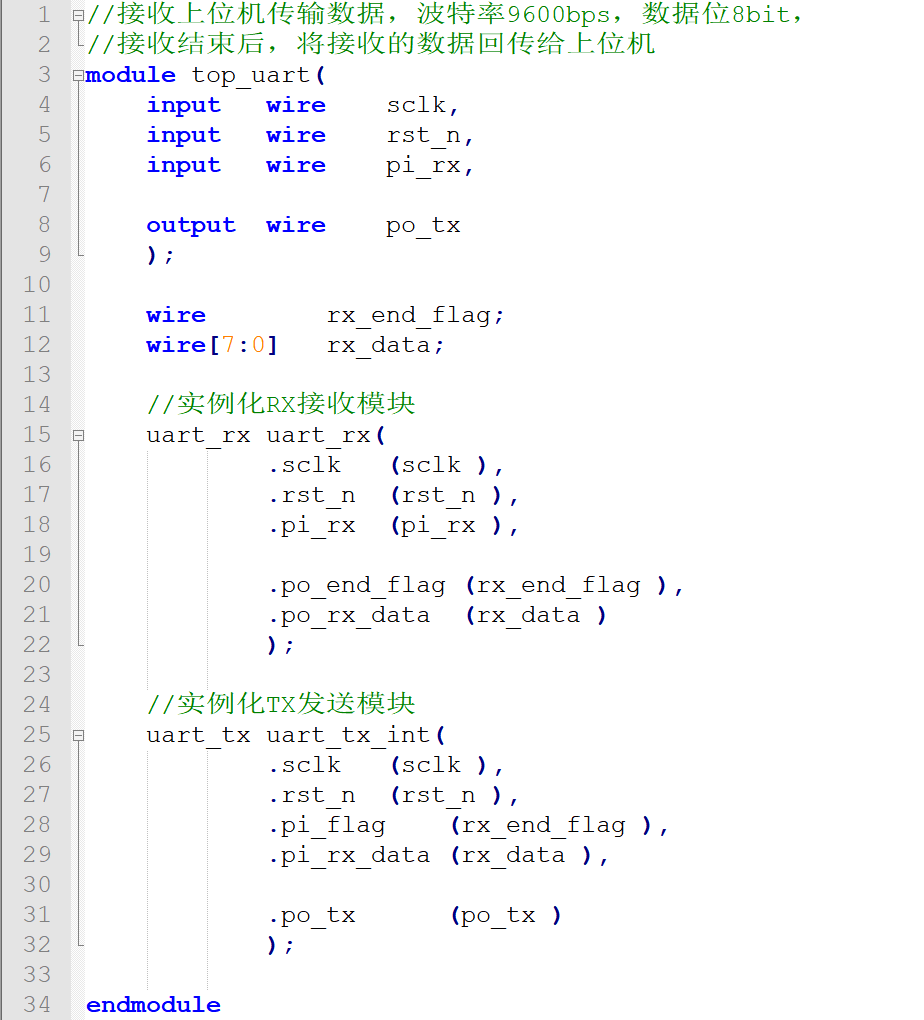
FPGA入门系列13--异步串口通信
文章简介 本系列文章主要针对FPGA初学者编写,包括FPGA的模块书写、基础语法、状态机、RAM、UART、SPI、VGA、以及功能验证等。将每一个知识点作为一个章节进行讲解,旨在更快速的提升初学者在FPGA开发方面的能力,每一个章节中都有针对性的代码…...
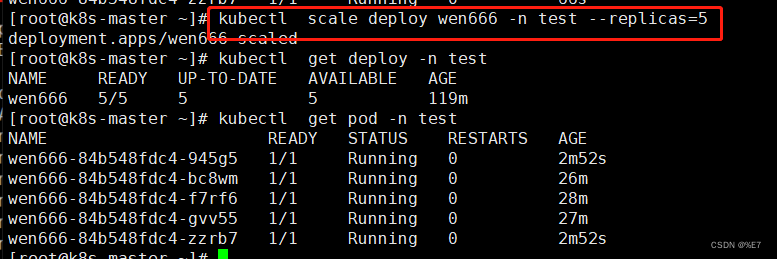
k8s基础4——deployment控制器、应用部署、升级、回滚、水平扩容缩容
文章目录 一、基本介绍二、应用程序生命周期2.1 部署应用2.2 应用升级2.2.1 修改YAML文件升级(交互式)2.2.2 命令指定镜像版本升级(免交互式)2.2.3 调用vim升级 2.3 滚动升级2.3.1 升级流程 2.4 应用回滚2.4.1 查看历史发布版本2.…...
动态规划算法——40道leetcode实例入门到熟练
目录 t0.解题五部曲1.基础入门题目1.509. 斐波那契数2.70. 爬楼梯3.746. 使用最小花费爬楼梯4.62. 不同路径5.63. 不同路径 II6.343. 整数拆分7.96. 不同的二叉搜索树 2.背包问题1.01背包(二维数组实现)2.01背包(滚动数组实现)1.4…...

Nmap入门到高级【第十一章】
预计更新第一章. Python 简介 Python 简介和历史Python 特点和优势安装 Python 第二章. 变量和数据类型 变量和标识符基本数据类型:数字、字符串、布尔值等字符串操作列表、元组和字典 第三章. 控制语句和函数 分支结构:if/else 语句循环结构&#…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
