快速排序、希尔排序、归并排序、堆排序、插入排序、冒泡排序、选择排序(递归、非递归)C语言详解

1.排序的概念及其运用

1.1排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

内部排序：数据元素全部放在内存中的排序。

外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

1.2排序运用

1.3 常见的排序算法

// 排序实现的接口// 插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 选择排序
void SelectSort(int* a, int n);// 堆排序
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n)// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right);
// 快速排序挖坑法
int PartSort2(int* a, int left, int right);
// 快速排序前后指针法
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int left, int right);// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)// 归并排序递归实现
void MergeSort(int* a, int n)
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)// 计数排序
void CountSort(int* a, int n)// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int)*N);int* a2 = (int*)malloc(sizeof(int)*N);int* a3 = (int*)malloc(sizeof(int)*N);int* a4 = (int*)malloc(sizeof(int)*N);int* a5 = (int*)malloc(sizeof(int)*N);int* a6 = (int*)malloc(sizeof(int)*N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N-1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);
}

排序OJ(可使用各种排序跑这个OJ)OJ链接

2.常见排序算法的实现

2.1 插入排序

2.1.1基本思想：

直接插入排序是一种简单的插入排序法，其基本思想是：

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列 。

实际中我们玩扑克牌时，就用了插入排序的思想

2.1.2直接插入排序：

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移

直接插入排序的特性总结：

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定

//插入排序
void InsertSort(int* a, int length)
{for (int i = 1; i < length; i++){int end = i - 1;int num = a[i];while (end >= 0){if (num < a[end]){a[end + 1] = a[end];//挪动数组end--;}else{break;//找到了要插入的点}}a[end + 1] = num;}
}

2.1.3 希尔排序( 缩小增量排序 )

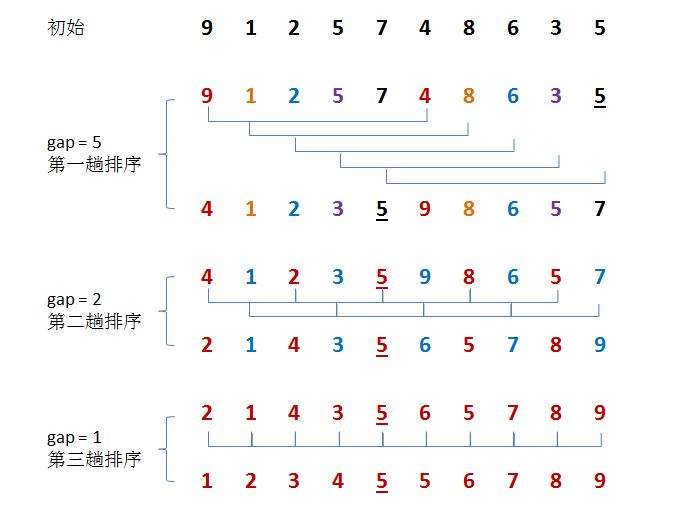
希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

//希尔排序
void ShellSort(int* a, int length)
{//接近有序int gap = length;while (gap > 1){gap /= 2;for (int i = 0; i < length - gap; i++){int end = i;int num = a[i + gap];while (end >= 0){if (a[end] > num){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = num;}}
}

希尔排序的特性总结：

1. 希尔排序是对直接插入排序的优化。

2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。

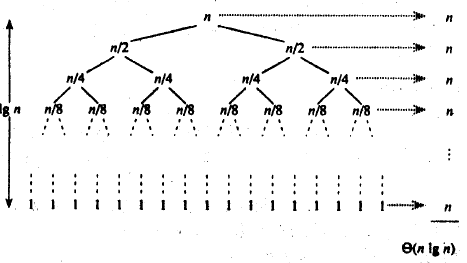
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定：

《数据结构(C语言版)》— 严蔚敏

《数据结构-用面相对象方法与C++描述》— 殷人昆

因为咋们的gap是按照Knuth提出的方式取值的，而且Knuth进行了大量的试验统计，我们暂时就按照：$O(n^{1.25})$ 到 $O(1.6\ast n^{1.25})$来算。

4. 稳定性：不稳定

2.2 选择排序

2.2.1基本思想：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

2.2.2 直接选择排序:

• 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素

• 若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换

• 在剩余的array[i]–array[n-2]（array[i+1]–array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

//选择排序
void SelectSort(int* a, int length)
{int left = 0, right = length - 1;while (left < right){int maxi = left, mini = left;for (int i = left + 1; i <= right; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[left], &a[mini]);if (left == maxi) maxi = mini;Swap(&a[right], &a[maxi]);left++;right--;}
}

直接选择排序的特性总结：

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

2.2.3 堆排序

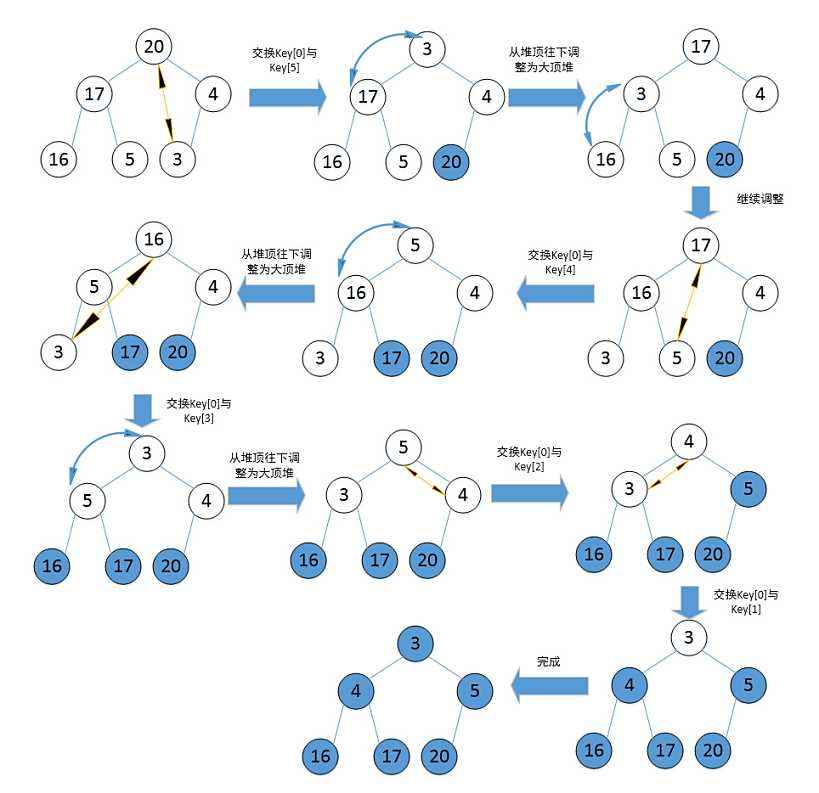
堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

//堆排序
void AdjustDown(int* a, int sz, int parent)
{//调大堆assert(a);int child = parent * 2 + 1;while (child < sz)//儿子节点要存在{//找左右儿子中最大的那个if (child + 1 < sz && a[child] < a[child + 1]){child++;//找到了最大的那个}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void SetHeap(int* a, int sz)
{assert(a);for (int i = (sz - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, sz, i);}
}void heap_sort(int* a, int sz)
{int num = sz;SetHeap(a, sz);while (num){Swap(&a[0], &a[num-1]);num--;AdjustDown(a, num, 0);}
}

直接选择排序的特性总结：

1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

2.3 交换排序

基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

2.3.1冒泡排序

//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){bool exchange = false;for (int j = 0; j < n - i - 1; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);exchange = true;}}if (exchange == false){break;}}
}

冒泡排序的特性总结：

1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定

2.3.2 快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基准值对array数组的 [left, right)区间中的元素进行划分int div = partion(array, left, right);// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}

上述为快速排序递归实现的主框架，发现与二叉树前序遍历规则非常像，同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来，后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。

将区间按照基准值划分为左右两半部分的常见方式有：

1. hoare版本

//hoare版本
void QuickSort(int* a, int left,int right)
{if (left >= right) return;int begin = left, end = right;int keyi = left;int mid = GetMid(a, left, right);Swap(&a[left], &a[mid]);while (left < right){while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = right;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}

2. 挖坑法

//挖坑法
void QuickSort(int* a, int left, int right)
{if (left >= right) return;int key = a[left];int begin = left, end=right;while (left < right){while (left < right && a[right] >= key){right--;}a[left] = a[right];while (left < right && a[left] <= key){left++;}a[right] = a[left];}a[left] = key;int keyi = left;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}

3. 前后指针版本

//前后指针快速排序
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int cur = left + 1, prev = left;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && cur > prev){prev++;Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[keyi]);int mid = prev;QuickSort(a, left, mid - 1);QuickSort(a, mid+1, right);
}

2.3.2 快速排序优化

1. 三数取中法选key

int GetMid(int* a,int left,int right)
{int mid = left + right >> 1;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else//a[left]>a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[mid]){return left;}else{return right;}}
}

1. 递归到小的子区间时，可以考虑使用插入排序

//小区间优化
void QuickSort(int* a, int left, int right)
{if (left >= right){return;}if ((right - left + 1) > 10){int cur = left + 1, prev = left;int keyi = left;while (cur <= right){if (a[cur] < a[keyi] && cur > prev){prev++;Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[keyi]);int mid = prev;QuickSort(a, left, mid - 1);QuickSort(a, mid + 1, right);}else{InsertSort(a + left, right - left + 1);}
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rFA7yHte-1683775858014)(C:/Users/19735/Desktop/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E5%88%9D%E9%98%B6V5-2021%E4%BF%AE%E8%AE%A2/Lesson6–%E6%8E%92%E5%BA%8F/11.jpg)]

2.3.2 快速排序非递归

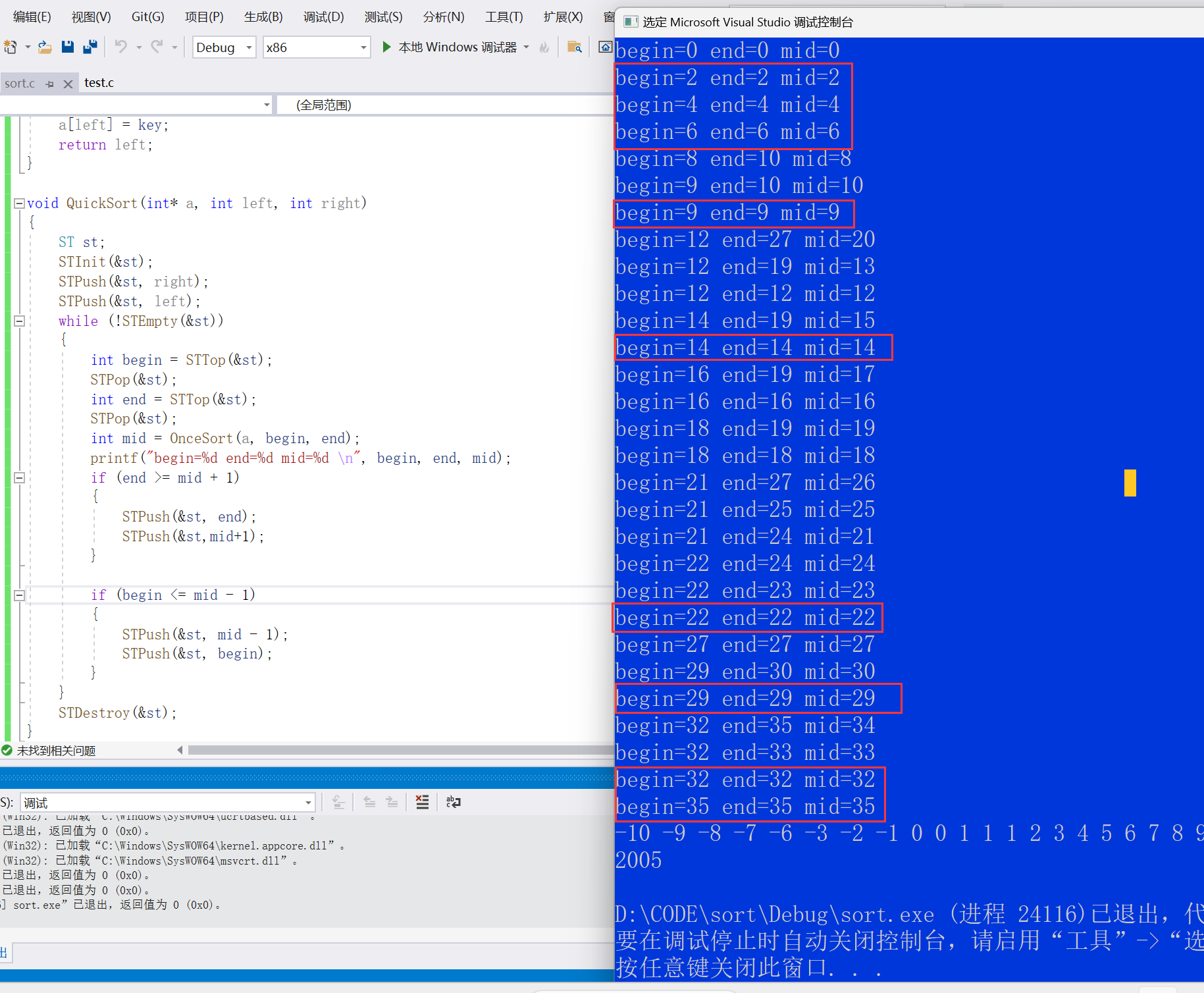
void QuickSortNonR(int* a, int left, int right)
{Stack st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (StackEmpty(&st) != 0){right = StackTop(&st);StackPop(&st);left = StackTop(&st);StackPop(&st);if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基准值为分割点，形成左右两部分：[left, div) 和 [div+1, right)StackPush(&st, div+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, div);}StackDestroy(&s);
}

int OnceSort(int* a, int left, int right)
{if (left > right){return;}int key = a[left];while (left < right){//先算右边，右边找大while (left<right&&a[right] >= key){right--;}//找到了就交换a[left] = a[right];while (left<right&&a[left] <= key){left++;}a[right] = a[left];}a[left] = key;//将key放在正确的位置上int meeti = left;//相遇的点return meeti;
}void QuickSort(int* a, int left, int right)
{ST st;//创建一个栈来模拟递归的过程STInit(&st);STPush(&st,right);STPush(&st,left);while (!STEmpty(&st)){//左区间int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int mid = OnceSort(a, begin, end);if(end > mid + 1){STPush(&st, end);STPush(&st, mid + 1);}//如果left>=mid-1说明左边已经排完序了if(begin < mid - 1){STPush(&st,mid - 1);STPush(&st, begin);}}STDestroy(&st);
}

在这里判断if语句的条件为什么不取=号呢？

假如我们取了等于号：

会出现很多没必要的判断，begin和end相等的时候就是只有一个元素，一个元素是不需要排序的，所以不用取=号

如果没有取=号的话：

快速排序的特性总结：

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(logN)

4. 稳定性：不稳定

2.4 归并排序

基本思想：

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
归并排序核心步骤：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-svQBGJGJ-1683775858015)(C:/Users/19735/Desktop/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E5%88%9D%E9%98%B6V5-2021%E4%BF%AE%E8%AE%A2/Lesson6–%E6%8E%92%E5%BA%8F/12.jpg)]

//归并排序递归
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end){return;}int mid = begin + end >> 1;_MergeSort(a, begin, mid,tmp);_MergeSort(a, mid+1, end,tmp);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}//处理剩余的while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int sz)
{int* tmp = (int*)malloc(sizeof(int) * sz);if (tmp == NULL){perror("malloc fail");exit(-1);}_MergeSort(a, 0, sz - 1, tmp);free(tmp);
}

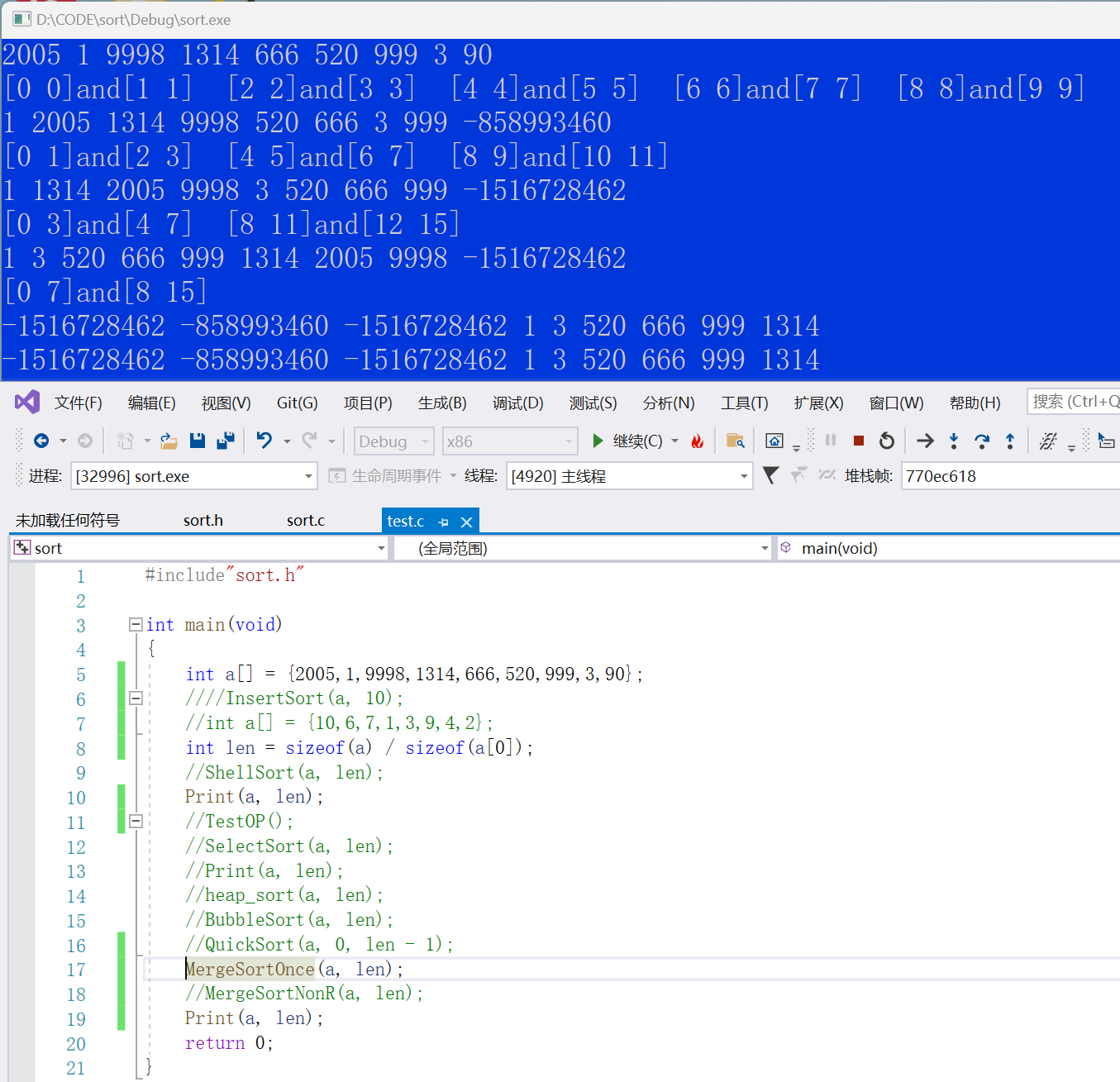
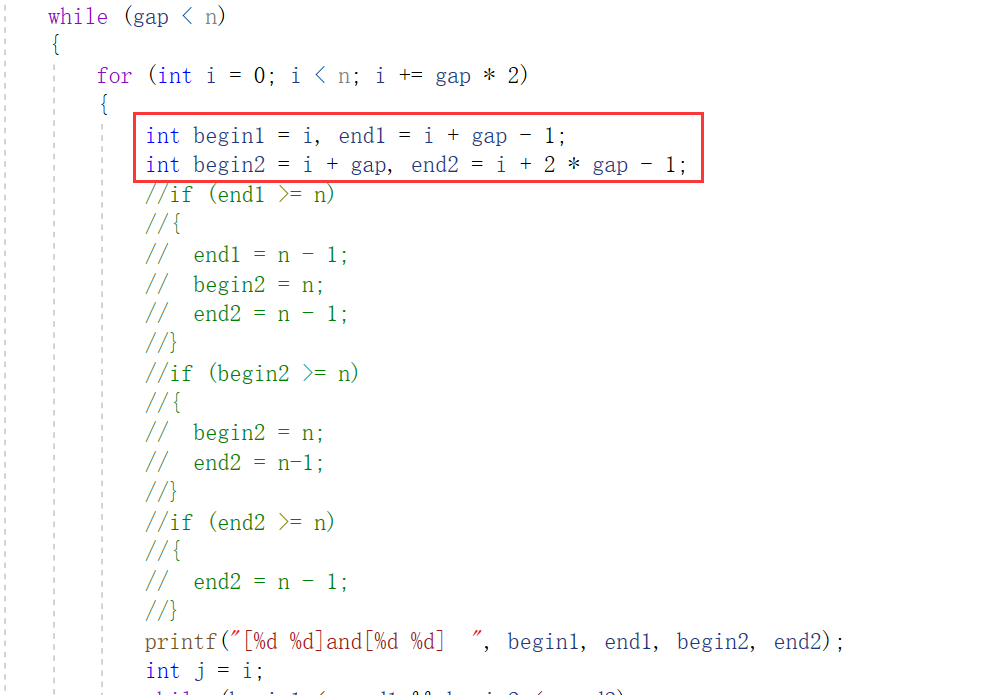
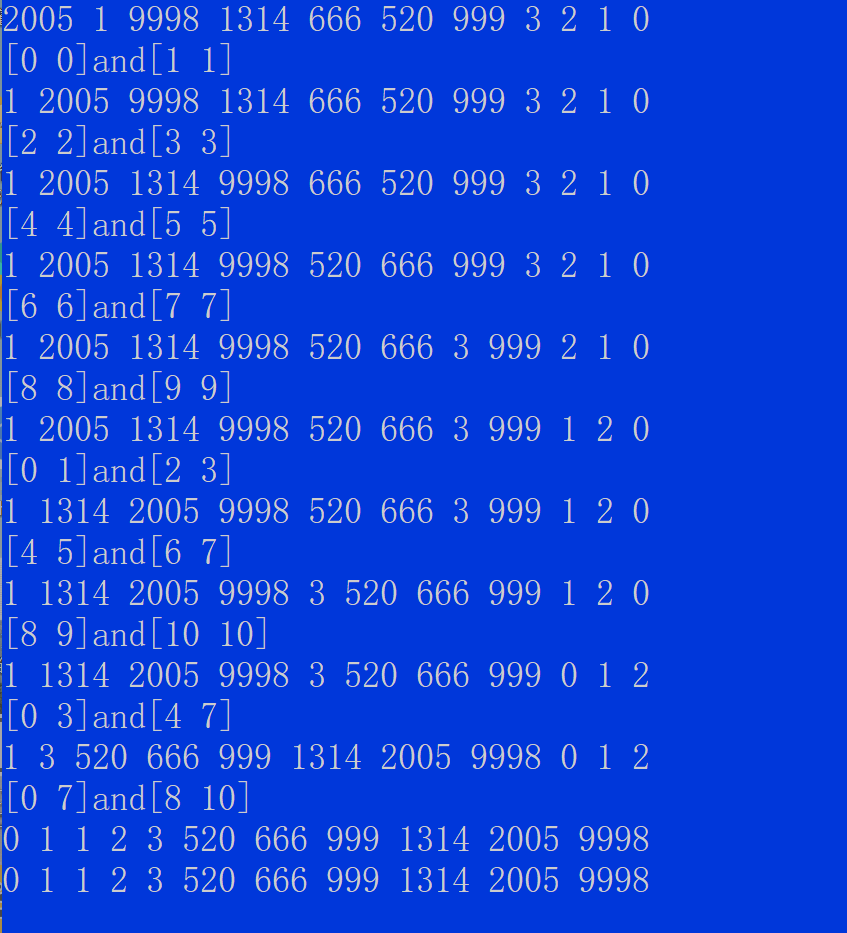
//归并排序非递归
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}int gap = 1;//分组，组间距while (gap < n){for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int j = i;if (begin1>=n||end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}printf("[%d %d] [%d %d]\n", begin1, end1, begin2, end2);while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);
}

如果不对区间进行修正：

可以看到原数组本来只有9个元素，有效区间是[0,8]但上述运行中明显有超过这个区间的区间，那这是什么原因导致的呢？

框框中的代码当gap很大的时候就会产生越界，但由于begin2依旧满足小于end2所以程序会继续进行

代码运行过程：

归并排序的特性总结：

1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定

2.5 非比较排序

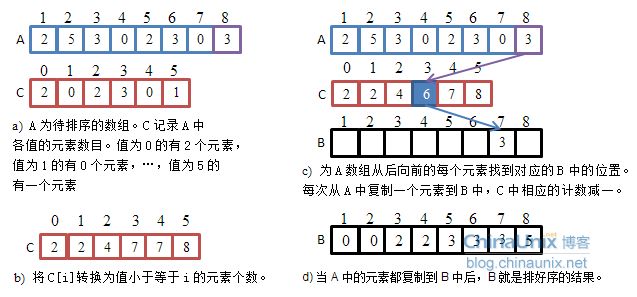
思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。
操作步骤：

1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

//计数排序
void CountSort(int* a, int n)
{int max = a[0], min = a[0];for (int i = 1; i < n; ++i){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;int* countA = (int*)malloc(sizeof(int) * range);if (countA == NULL){perror("malloc fail\n");return;}memset(countA, 0, sizeof(int) * range);// 计数for (int i = 0; i < n; i++){countA[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (countA[i]--){a[j++] = i + min;}}free(countA);
}

计数排序的特性总结：

1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(MAX(N,范围))
3. 空间复杂度：O(范围)
4. 稳定性：稳定

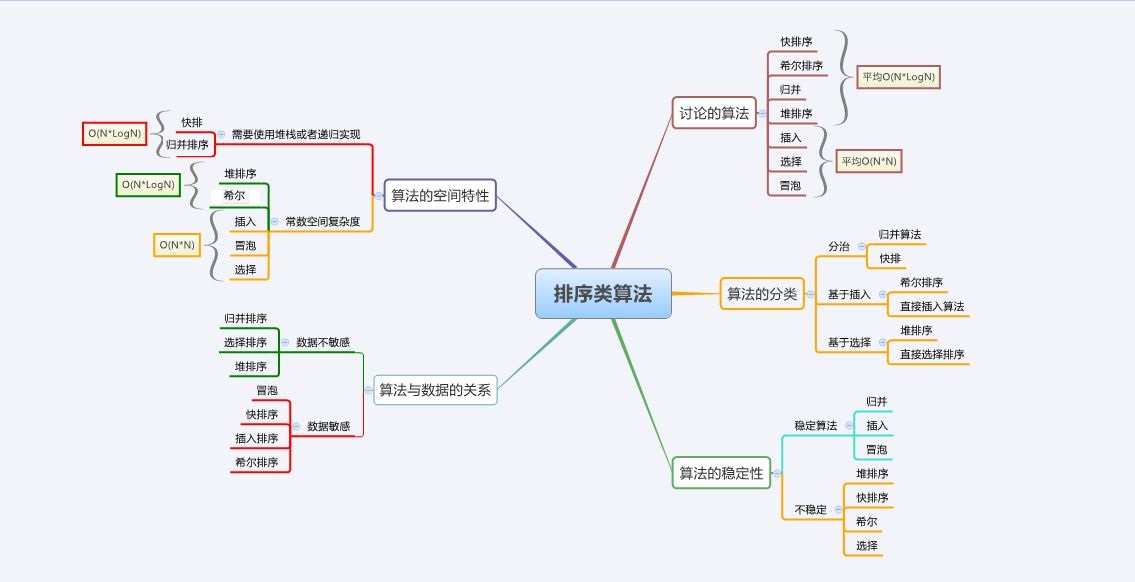
3.排序算法复杂度及稳定性分析

4.选择题练习

1. 快速排序算法是基于（    ）的一个排序算法。
A 分治法
B 贪心法
C 递归法
D 动态规划法2.对记录（54,38,96,23,15,72,60,45,83）进行从小到大的直接插入排序时，当把第8个记录45插入到有序表时，为找到插入位置需比较（ ）次？（采用从后往前比较）
A 3
B 4
C 5
D 63.以下排序方式中占用O（n）辅助存储空间的是
A 选择排序
B 快速排序
C 堆排序
D 归并排序4.下列排序算法中稳定且时间复杂度为O(n2)的是（ ）
A 快速排序
B 冒泡排序
C 直接选择排序
D 归并排序5.关于排序，下面说法不正确的是
A 快排时间复杂度为O(N*logN)，空间复杂度为O(logN)
B 归并排序是一种稳定的排序,堆排序和快排均不稳定
C 序列基本有序时，快排退化成冒泡排序，直接插入排序最快
D 归并排序空间复杂度为O(N), 堆排序空间复杂度的为O(logN)6.下列排序法中，最坏情况下时间复杂度最小的是（ ）
A 堆排序
B 快速排序
C 希尔排序
D 冒泡排序7.设一组初始记录关键字序列为(65,56,72,99,86,25,34,66)，则以第一个关键字65为基准而得到的一趟快速排序结果是（）
A 34，56，25，65，86，99，72，66
B 25，34，56，65，99，86，72，66
C 34，56，25，65，66，99，86，72
D 34，56，25，65，99，86，72，66

答案：
1.A
2.C
3.D
4.B
5.D
6.A
7.A