小猪,信息论与我们的生活
前言
动态规划是大家都熟悉与陌生的知识,非常灵活多变,我自己也不敢说自己掌握了,今天给大家介绍一道题,不仅局限于动态规划做题,还会上升到信息论,乃至于启发自己认知世界的角度
因为比较难,本文不会详细介绍动态规划方法,所以需要读者有一定基础,否则可能理解有困难
题目链接:可怜的小猪
有 buckets 桶液体,其中 正好有一桶 含有毒药,其余装的都是水。它们从外观看起来都一样。为了弄清楚哪只水桶含有毒药,你可以喂一些猪喝,通过观察猪是否会死进行判断。不幸的是,你只有 minutesToTest 分钟时间来确定哪桶液体是有毒的。
喂猪的规则如下:
- 选择若干活猪进行喂养
- 可以允许小猪同时饮用任意数量的桶中的水,并且该过程不需要时间。
- 小猪喝完水后,必须有
minutesToDie分钟的冷却时间。在这段时间里,你只能观察,而不允许继续喂猪。 - 过了
minutesToDie分钟后,所有喝到毒药的猪都会死去,其他所有猪都会活下来。 - 重复这一过程,直到时间用完。
给你桶的数目 buckets ,minutesToDie 和 minutesToTest ,返回 在规定时间内判断哪个桶有毒所需的 最小 猪数 。
示例 1:
输入: buckets = 1000, minutesToDie = 15, minutesToTest = 60
输出: 5
示例 2:
输入: buckets = 4, minutesToDie = 15, minutesToTest = 15
输出: 2
示例 3:
输入: buckets = 4, minutesToDie = 15, minutesToTest = 30
输出: 2
dp解析
一般来说,动态规划就是三步骤
- 定义数组含义,多数情况是int值, dp[]或者dp[][]
- 赋予初始值
- 找到状态转移方程,开始递推
推到最后,大部分情况下,dp数组最后一个值就是答案
这个题,
题中有buckets,minutesToTest,minutesToDie三个变量,由于正面角度比较难思考,可以反过来,
全问题为n只小猪,能够有限的轮次测试中测出毒药,一轮耗时minutesToDie,总轮数为minutesToTest/minutesToDie
所以,其子问题为i只小猪测试j轮的结果,不影响后续测试,而后续测试需要子问题的结果来递推
满足动态规划的重叠子问题和无后效性原则,同时又是求最值(简称n),所以确定可以用动态规划(简称dp)
- 首先定义数组含义
f(i, j)表示i只小猪,测试j轮后最多可以在多少butkets中找到毒药,显然,这是一个二维数组dp[i][j] - 然后赋予初始值
dp[0][0] , dp[i][0]都为1,相当于没有测试,因为知道必有一桶毒,所以bucket = 1时,可以肯定为有毒,dp[0][j]没有猪,也全为1 - 状态转移
假设现在状态要算f(i, j),一轮测试后还剩下k只猪存活,而测试剩下j - 1次,可以确定,f(k, j - 1)就是f(i, j )的前一个状态,并将递推出f(i, j)
从i变为k的可能组合数为 C(i, k),因此f(i, j) = C(i, k) * f(k, j - 1),其中k的取值为0~i,所以最后的计算如下
f ( i , j ) = ∑ k = 0 i f ( k , j − 1 ) × C i k f(i,j) = \sum_{k=0}^i f(k, j-1) \times C_{i}^{k} f(i,j)=k=0∑if(k,j−1)×Cik
到了这步,已经掌握了解题钥匙,更多细节可以参考题解
本文并非想详细介绍题解,更多的是探讨思想
信息论
抛开dp的过程,只看开始和结尾,buckets,minutesToTest,minutesToDie都限定后,通过递推或者某种方式,我们就能得到最少的猪数量n,也就是说,当相关信息量确认好后,答案就确定了
这给我们一个很大提示,那就是,面对一个问题的时候,在耗费时间去做之前,仅仅凭借已经掌握的信息,就能判断出能不做成。注意,这里不是靠经验或者直觉,而是真真实实的科学,若是吸收这一思想,并勤加练习,相当多的难题可以得到解决
那现在我们就来仔细了解下这一理论吧
我们知道,计算机的很多数据看不见摸不着,我们将其统一设置为二进制,使用bit来记录数据,创造纷繁的信息世界。而我们,不知道三维世界的造物主用的几进制,在这个世界的我们无法用自己的信息来精确表达信息本身
熵
不过没关系,我们可以一个模糊的“熵”暂时代替,表示混乱度,越混乱,熵越高
熵增定律:在一个孤立系统里,如果没有外力做功,其总混乱度(熵)会不断增大
对于理科生很好理解,毕竟学过
对于保洁也很好理解,毕竟一个房间如果长期不打扫,肯定会变脏
对于老师也很好理解,毕竟他如果长时间不来教室,教室肯定乱套
对于宅男更好理解,长期不外出不和人交流,一定……
信息熵与信息
在信息论中,信息熵表示信息的不确定程度
比如,我们都知道,同样的内容,中文写的往往比英文薄一些,实际上,就是因为中文的信息不确定程度高,也就是信息熵大,所以所需的信息量就会少,字数也会少,往往掌握1000个汉字就能应付日常说话,很多汉字在不同的组词下有大量不同的含义。而英文,掌握5000单词都未必能说清楚
但是信息熵大未必是好事,信息熵越大,不确定程度越高,其实代表信息量越少,而减少信息熵的方式,就是增加含信息量的信息,不含信息量的信息,可以归类为废话(说到这,我都不认识信息两字了)
所以方向来了!对于一件富含信息熵的事情,我只要掌握足够信息量的信息,与信息熵等价,那么就可以做!
比如,明天是否下雨?,这件事信息熵很大,天气预报的结果,天上的乌云,蚂蚁搬家等等都是多多少少降低信息熵的信息
到了这里,你可以还是会有疑惑,说来说去,最后不还是靠感觉吗?不过是用了一些科学名词归类而已
香农厉害就厉害在这里,讲一个千万年来人说不清的感觉提取出公式,让人类的认知进入了一个全新领域。在信息论提出之后,个人认为能与这一瞬间媲美的只有阿姆斯特朗的那一小步。
公式如下
H ( X ) = − ∑ i = 1 n p ( x i ) log b p ( x i ) H(X) = -\sum_{i=1}^n p(x_i)\log_b p(x_i) H(X)=−i=1∑np(xi)logbp(xi)
看起来挺复杂,但是理解很简单,
其中,H(X)表示随机变量X的信息熵,P(xi)表示X取值为xi的概率,logb表示以b为底的对数。
这里的b表示信息单位的基础,如果你想二进制表示,那么b == 2
x表示事件,xi可以理解为x里面的某种元素,公式就是将X事件中,1~n种元素发生的概率求和而来,n可以理解为可能的所有情况
比如扔一枚硬币,只有两种情况,那么其信息熵为
H ( X ) = − ∑ i = 1 2 p ( x i ) log 2 p ( x i ) = − [ 0.5 log 2 ( 0.5 ) + 0.5 log 2 ( 0.5 ) ] = 1 b i t H(X) = -\sum_{i=1}^2 p(x_i)\log_2 p(x_i) = -\left[0.5\log_2(0.5) + 0.5\log_2(0.5)\right] = 1 bit H(X)=−i=1∑2p(xi)log2p(xi)=−[0.5log2(0.5)+0.5log2(0.5)]=1bit
也就是说,只要有一个含1bit信息量的信息,就可以消灭信息熵,比如我告诉你,硬币为正面,此时,信息熵消失
解题
回到小猪的话题,题目充满了H(X)信息熵,在minutesToTest,minutesToDie限定下,X为bucket数,x为1000时
H = − ( 1 / 1000 ) ∗ l o g 2 ( 1 / 1000 ) − ( 1 / 1000 ) ∗ l o g 2 ( 1 / 1000 ) − . . . − ( 1 / 1000 ) ∗ l o g 2 ( 1 / 1000 ) H = - (1/1000) * log2(1/1000) - (1/1000) * log2(1/1000) - ... - (1/1000) * log2(1/1000) H=−(1/1000)∗log2(1/1000)−(1/1000)∗log2(1/1000)−...−(1/1000)∗log2(1/1000)
= − 1000 ∗ ( 1 / 1000 ) ∗ l o g 2 ( 1 / 1000 ) = l o g 2 ( 1000 ) ≈ 9.97 = - 1000 * (1/1000) * log2(1/1000) = log2(1000) ≈ 9.97 =−1000∗(1/1000)∗log2(1/1000)=log2(1000)≈9.97
我们可以对这个结果有些感性认识,看起来信息熵的增长不是线性的,而是log,扔硬币这种五五开的事情为1,而1000桶水找1个有毒居然只有9.97,当有10000桶水时,信息熵为log2(10000) = 13.29
现在我们就要考虑,多少小猪能提供超过9.97
参考链接:https://www.zhihu.com/question/60227816/answer/1274071217
https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)
相关文章:

小猪,信息论与我们的生活
前言 动态规划是大家都熟悉与陌生的知识,非常灵活多变,我自己也不敢说自己掌握了,今天给大家介绍一道题,不仅局限于动态规划做题,还会上升到信息论,乃至于启发自己认知世界的角度 因为比较难,本…...
【鸿蒙应用ArkTS开发系列】- http网络库使用讲解和封装
目录 前言http网络库组件介绍http网络库封装创建Har Module创建RequestOption 配置类创建HttpCore核心类创建HttpManager核心类对外组件导出添加网络权限 http网络库依赖和使用依赖http网络库(httpLibrary)使用http网络库(httpLibrary&#x…...

【Java零基础入门篇】第 ⑥ 期 - 异常处理
博主:命运之光 专栏:Java零基础入门 学习目标 掌握异常的概念,Java中的常见异常类; 掌握Java中如何捕获和处理异常; 掌握自定义异常类及其使用; 目录 异常概述 异常体系 常见的异常 Java的异常处理机制…...

计算职工工资
目录 问题描述 程序设计 问题描述 【问题描述】 给定N个职员的信息,包括姓名、基本工资、浮动工资和支出,要求编写程序顺序输出每位职员的姓名和实发工资(实发工资=基本工资+浮动工资-支出)。 【输入形式】 输入在一行中给出正整数N。随后N行,每行给出一位职员的信息,…...

2019年上半年软件设计师下午试题
试题四(共 15 分) 阅读下列说明和 C 代码,回答问题 1 至 3,将解答写在答题纸的对应栏内 【说明】 n 皇后问题描述为:在一个 n*n 的棋盘上摆放 n 个皇后,要求任意两个皇后不能冲突, 即任意两个皇后不在同一行、同一列或者同一斜…...

IS200TPROH1BCB用于工业应用和电力分配等。高压型隔离开关用于变电站
IS200TPROH1BCB用于工业应用和电力分配等。高压型隔离开关用于变电站 什么是隔离器,它与断路器有何不同 什么是隔离器,为什么要使用隔离器 隔离器是一种开关装置,它可以手动或自动操作,隔离一部分电能。隔离器可用于在无负载情…...
【MySql】数据库 select 进阶
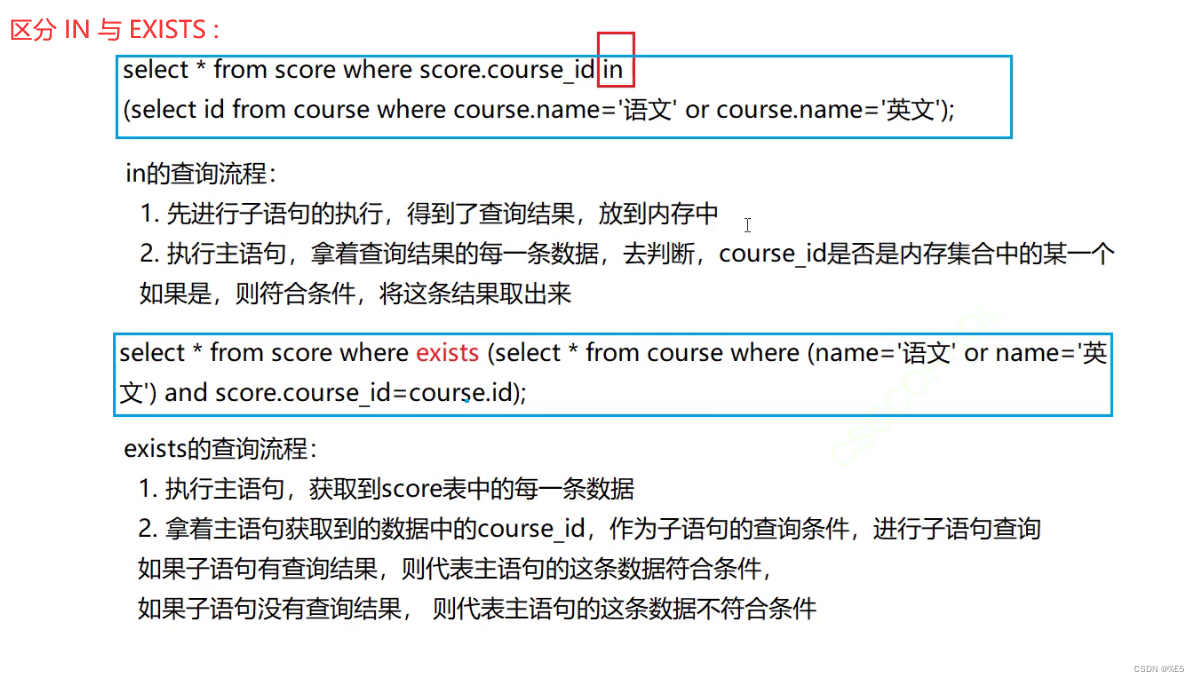
数据库 数据库表的设计ER 关系图三大范式 聚合函数与分组查询聚合函数 (count、sum、avg、max、min)分组查询 group by fields....having....(条件) 多表联查内连接外连接(左连接,右连接)自连接子查询合并查询 UNION 数据库表的设计 ER 关系…...

CVPR 2023 | VoxelNeXt实现全稀疏3D检测跟踪,还能结合Seg Anything
在本文中,研究者提出了一个完全稀疏且以体素为基础的3D物体检测和跟踪框架VoxelNeXt。它采用简单的技术,运行快速,没有太多额外的成本,并且可以在没有NMS后处理的情况下以优雅的方式工作。VoxelNeXt在大规模数据集nuScenes、Waymo…...
本地使用3台centos7虚拟机搭建K8S集群教程
第一步 准备3台centos7虚拟机 3台虚拟机与主机的网络模式都是桥接的模式,也就是他们都是一台独立的“主机” (1)kebe-master的配置 虚拟机配置: 网络配置: (2)kebe-node1的配置 虚拟机配…...

NVIDIA CUDA驱动安装
1 引言 因为笔记本电脑上运行Milvus图像检索代码,需要安装CUDA驱动。电脑显卡型号是NVIDIA GeForce GTX 1050 Ti Mobile, 操作系统是Ubuntu 20.04,内核版本为Linux 5.15.0-72-generic。 2 CUDA驱动测试 参考网上的资料:https://blog.csdn.…...

python 从excel中获取需要执行的用例
classmethod def get_excel_data(cls, excel_name, sheet_name, case_numNone):"""读取excel文件的方法:param excel_name: 文件名称:param sheet_name: sheet页的名称:param case_name: 执行的case名称:return:"""def get_row_data(table, row)…...

Web3中文|乱花渐欲meme人眼,BRC-20总市值逼近10亿美元
现在的Web3加密市场,用“乱花渐欲meme人眼”来形容再合适不过了。 何为meme? “meme”这个词大概很多人都不知道如何正确发音,并且一看到它就会和狗狗币Dogecoin等联系在一起。那它究竟从何而来呢? Meme:[mi:m]&#x…...

盖雅案例入选「首届人力资源服务国际贸易交流合作大会20项创新经验」
近日,首届人力资源服务国际贸易交流合作大会顺利召开。为激励企业在人力资源服务贸易领域不断创新,加快培育对外贸易新业态、新模式,形成人力资源服务领域国际竞争新优势,大会评选出了「首届人力资源服务国际贸易交流合作大会20项…...

[论文笔记]SimMIM:a Simple Framework for Masked Image Modeling
文章地址:https://arxiv.org/abs/2111.09886 代码地址:https://github.com/microsoft/SimMIM 文章目录 摘要文章思路创新点文章框架Masking strategyPrediction headPrediction targetEvaluation protocols 性能实验实验设置Mask 策略预测头目标分辨率预…...
----索引/视图/范式)
mysql从零开始(4)----索引/视图/范式
接上文 mysql从零开始(3) 索引 索引是在数据库表的字段上添加的,是为了提高查询效率存在的一种机制。一张表的一个字段可以添加一个索引,也可以多个字段联合起来添加索引。索引相当于一本书的目录,是为了缩小扫描范围…...
Flutter框架:从入门到实战,构建跨平台移动应用的全流程解析
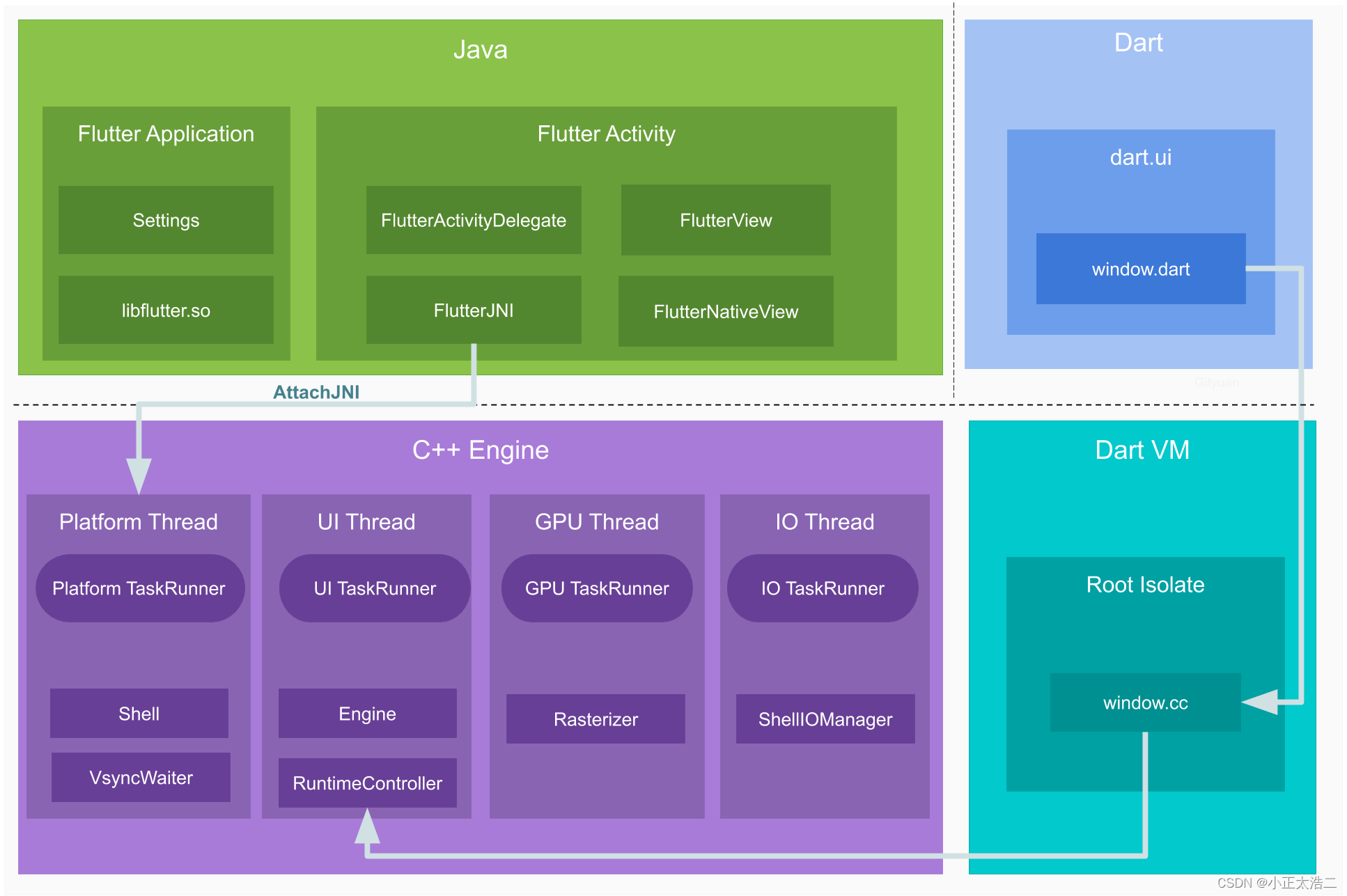
第一章:Flutter框架介绍 Flutter框架是由Google推出的一款跨平台移动应用开发框架。相比其他跨平台框架,Flutter具有更高的性能和更好的用户体验。本章将介绍Flutter框架的概念、特点以及与其他跨平台框架的比较,以及Flutter开发环境的搭建和…...

Spring AOP+注解方式实现系统日志记录
一、前言 在上篇文章中,我们使用了AOP思想实现日志记录的功能,代码中采用了指定连接点方式(Pointcut(“execution(* com.nowcoder.community.controller..(…))”)),指定后不需要在进行任何操作就可以记录日志了&…...

OpenGL 4.0的Tessellation Shader(细分曲面着色器)
细分曲面着色器(Tessellation Shader)处于顶点着色器阶段的下一个阶段,我们可以看以下链接的OpenGL渲染流水线的图:Rendering Pipeline Overview。它是由ATI在2001年率先设计出来的。 目录 细分曲面着色器细分曲面Patch细分曲面控…...

项目经理如何及时掌控项目进度?
延迟是指超出计划的时间,而无法掌控则意味着管理者对实际情况一无所知。 为了解决这些问题,我们需要建立好的制度和沟通机制。例如使用项目管理软件来跟踪进度、定期开会并避免沟通障碍等。 管理者可以建立相关制度: 1、建立进度记录制度。…...

HTML <applet> 标签
HTML5 中不支持 <applet> 标签在 HTML 4 中用于定义嵌入式小程序(插件)。 实例 一个嵌入的 Java applet: <applet code="Bubbles.class" width="350" height="350"> Java applet that draws animated bubbles. </applet&g…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
