分布式系统基础理论
CAP是分布式系统方向中的一个非常重要的理论,可以粗略的将它看成是分布式系统的起点,CAP分别代表的是分布式系统中的三种性质,分别是Consistency(可用性)、Availability(一致性)、Partition tolerance(网络分区容忍性),它们的第一个字母分别是C A P,于是这个理论被称为CAP理论
理论上来说,CAP三者同时最多满足两者,但是并不是必须满足两个,许多系统最多只能同时满足0、1个
为什么CAP最多只能满足两个呢?
我们可以以电商系统的两个集群来当做例子
C: 追求的是数据一致性 当有一个请求来了之后 它会等待网络隔离的情况结束之后 向另一个机器进行数据的同步
A: 追求的是可用性 也就是尽可能提供有效服务 当一个请求来了之后 它会立即返回 哪怕数据是陈旧的 也得优先提供服务,其他分区的节点返回的结果(数据)可能是不一样
注意:这里的AP不可同时满足指的是当整个分布式系统中出现网络隔离的时候,我们不能既想着保证数据的实时强一致性,又去追求服务的可用性。
但是当没有网络隔离的时候,其实这两个性质是可以同时满足的,因为『同步数据』和『返回结果』这两个操作都是在同一个网络中,只有先后关系,不会因为某个操作导致另一个操作的『死等』
在分布式系统中,P是会必然发生的,造成P的原因可能是网络隔离,也可能是节点宕机。
我们无法保证分布式系统每一时刻都不出现网络隔离,如果不满足P的特性,一旦发生分区错误,那么分布式系统就无法工作,这显然违背了分布式的理念,连最基本的分布式系统条件都没有满足
典型的CP和AP的产品
CP:Zookeeper 当系统在发生分区故障之后 客户端的所有请求都会被卡死或者超时 但是系统总会返回一致的数据
AP:Eureka 分区发生故障之后 客户端依然可以访问系统 但是获取的数据有的是新数据 有的是老数据
当然 CAP这几个特性不是BOOL类型的,而是一个范围类型,完全是看系统具体需要什么样的要求。
比如分区容错,有的系统一台机器出错,系统会认为不影响业务的话,认为分区不存在。只有多台机器都出问题了,系统受到严重影响才认为出现分区
PACELC理论
PACELC理论是对CAP理论的扩展,在维基百科上的定义是
It states that in case of network partitioning § in a distributed computer system, one has to choose between availability (A) and consistency © (as per the CAP theorem), but else (E), even when the system is running normally in the absence of partitions, one has to choose between latency (L) and consistency ©.
如果有分区(P),那么系统就必须在可用性(A)和一致性(C)之间取得平衡,否则(E),当系统运行在无分区的情况下,系统需要在延迟(L)和一致性(C)之间取得平衡
它相比于CAP,多引入了一个延迟Latency的概念,在出现分区错误的时候,取前半部分PAC,理论和CAP的内容一致。没有出现分区错误的时候取LC,也就是Latency与Consistency
当前分布式系统指导理论更替代CAP理论,理由如下
PACELC更能满足实际操作中分布式系统的工作场景,是更好的工程实现策略
当P存在的场景下,需要在A C之间做取舍,但是实际上分布式系统大部分时间里P是不存在的,那么在L和C之间做取舍是一个更好的选择
PACELC可以在latency与consistency之间获得平衡
要保证系统的高可用,那么就得采用冗余的思想,我的其他博文有提到4个9的异地多活策略,也是采用的数据冗余思想,而一旦涉及到了复制数据,在分布式中就一定会在Consistency和Latency之间做一个取舍
image.png
举个例子
在强一致性的场景下,需要三个从节点都落盘数据,才能给客户端返回OK,这个时候当master向slave同步数据的时候,超过20ms触发超时了,整个系统还是会不断的重试这个过程,这显然造成了系统的可用性比较低
所以我们一般都会在数据一致性和请求时延之间做一个balance
当同步超过五次之后,认为这个节点故障,选择直接返回,可以消除写时的长尾抖动,同时给节点打上故障标签,进行后续的处理
BASE理论
base理论是Basically Avaliable(基本可用)、Soft State(软状态)、Eventually Consistent(最终一致性)三个短语的缩写,核心思想如下
即使无法做到强一致性,但每个应用都可以根据自身的业务特点,采用适当的方式来使系统达到最终一致性
BA:基本可用指的是当系统出现了不可预知的故障,系统依旧可用,不过可用度也许会降低,比如响应时间上出现损失,功能上只能满足基本功能等等
S:基于原子性而言的话,当要求多个节点数据一致时,我们认为这是一种『硬』状态,而允许系统中的数据存在中间状态,并认为其不影响系统的整体可用性,即允许系统在多个不同节点的数据副本存在数据时延
E:最终一致性,系统不可能一直都处于一个软状态中,必须有个时间期限。在期限过后,应该保证所有副本保持数据一致性,从而达到数据的最终一致性。这个时间期限取决于时延、负载、方案等等
在工程实践中,有这么几种最终一致性的实现策略,通常都是多种策略混合实现
因果一致性:如果节点A在更新完某个数据后通知了节点B,那么节点B之后对该数据的访问和修改都是基于A更新后的值。与此同时,与节点A无因果关系的节点C的数据访问没有这样的限制
读已知所写:节点A更新一个数据之后,自身总是能访问到更新过的最新值,而不会访问旧值
会话一致性:将对系统数据的访问过程框定在了一个会话当中,系统能保证同一个有效的会话中实现客户端在一个会话中读取到该数据项永远是最新值
单调读一致性:如果一个节点从系统中读取出一个数据项的某个值之后,那么系统对于该节点后续的任何数据访问都不该返回更旧的值
单调写一致性:一个系统要能够保证来自同一个节点的写操作被顺序的执行。
相关文章:

分布式系统基础理论
CAP是分布式系统方向中的一个非常重要的理论,可以粗略的将它看成是分布式系统的起点,CAP分别代表的是分布式系统中的三种性质,分别是Consistency(可用性)、Availability(一致性)、Partition tol…...

HttpServletRequestWrapper的使用与原理
介绍 HttpServletRequestWrapper 实现了 HttpServletRequest 接口,可以让开发人员很方便的改造发送给 Servlet 的请求.HttpServletRequest 对参数值的获取实际调的是org.apache.catalina.connector.Request没有提供对应的set方法修改属性所以不能对前端传来的参…...
)
PBDB Data Service:List of fossil occurrences(化石产出记录列表)
List of fossil occurrences(化石产出记录列表) 描述用法参数选择PBDB所有记录(all_records)以下参数可用于按各种条件查询化石产出记录以下参数可用于筛选所选内容以下参数还可用于根据分类筛选结果列表以下参数可用于生成数据存…...

初识C语言
1. 初识C语言 C语言是一门通用计算机编程语言,广泛应用于底层开发。 C语言是一门面向过程的计算机编程语言,它与C,Java等面向对象的编程语言有所不同。 第一个C语言程序: #include<stdio.h>int main(void) {printf("hello worl…...
)
Leetcode 322. 零钱兑换(完全背包)
Leetcode 322. 零钱兑换(完全背包)题目 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额&…...
怎么恢复回收站?分享4个宝藏方法!
案例:怎么恢复回收站 【请问大家怎么恢复误删的文件呀?如果回收站被清空了,又应该怎么恢复呢?】 电脑回收站是我们存储被删除文件的地方。但是有时候,我们会不小心把一些重要的文件或者照片误删了。这时候࿰…...

大模型混战,最先实现“智慧涌现”的会是谁?
作者 | 曾响铃 文 | 响铃说 几秒钟写出了一篇欢迎词; 小说人物乱入现实,快速创作不重样的故事; 鼠标一点,一封英文工作沟通邮件撰写完成; 准确解出数学应用题,还给出解题步骤; 甚至还能理…...
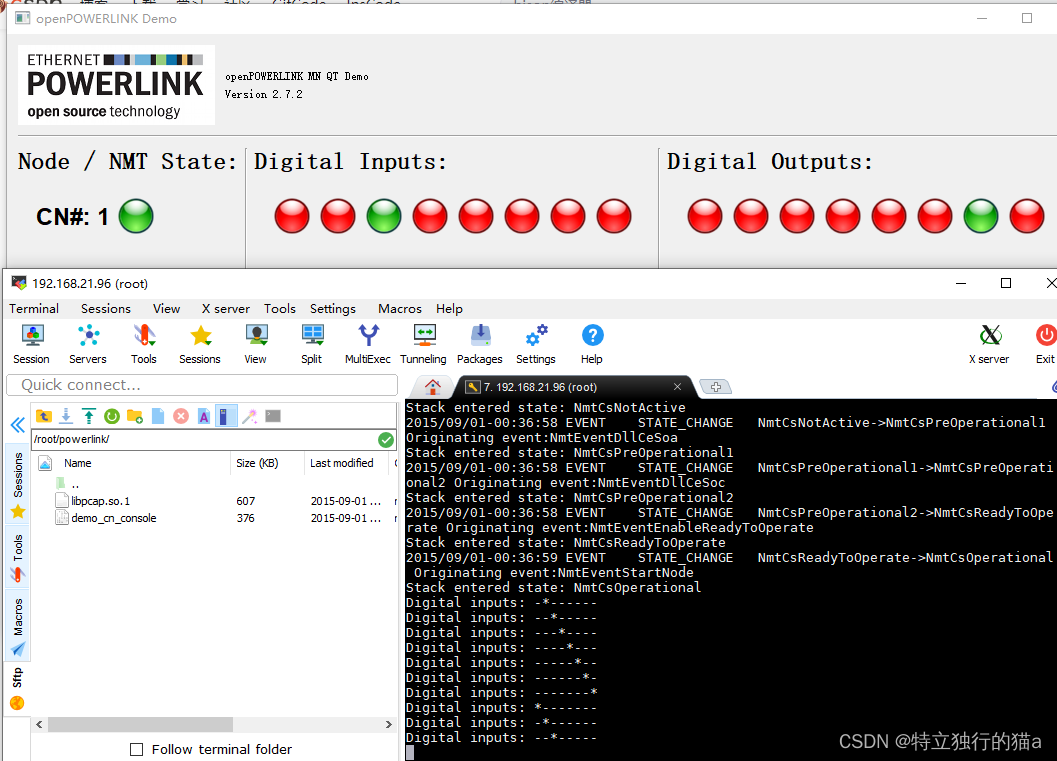
Powerlink协议在嵌入式linux上的移植和主从站通信(电脑和linux板通信实验)
使用最新的openPOWERLINK 2.7.2源码,业余时间搞定了Powerlink协议在嵌入式linux上的移植和测试,并进行了下电脑和linux开发板之间的通信实验。添加了一个节点配置,跑通了源码中提供的主站和从站的两个demo。这里总结下移植过程分享给有需要的…...
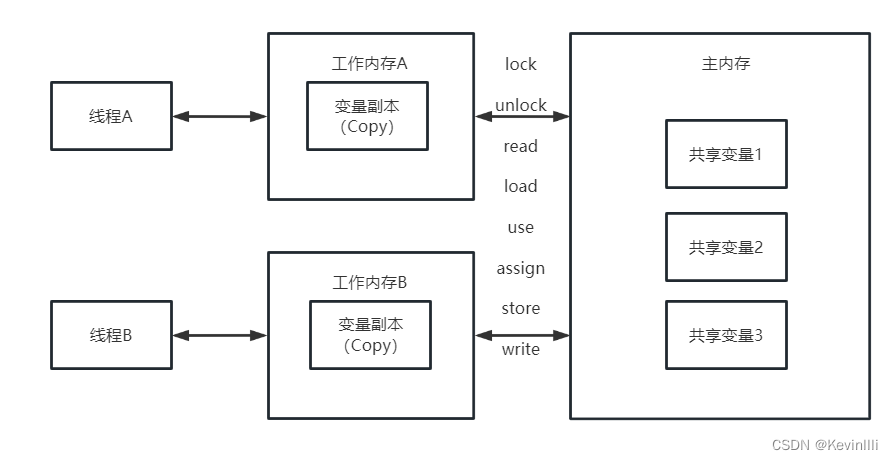
快速理解基本的cookie、session 和 redis
一、Cookie 1、什么是Cookie 1、Cookie实际上是一小段的文本信息,是一种keyvalue形式的字符串。客户端请求服务器,如果服务器需要记录该用户状态,就使用response向客户端浏览器颁发一个Cookie。客户端会把Cookie保存起来。 2、当浏览器再请求…...
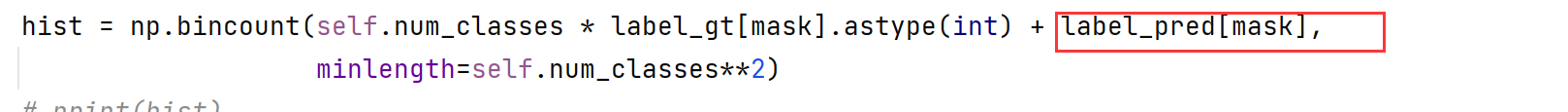
STANet代码复现出现的问题
1 IndexError: boolean index did not match indexed array along dimension 0; dimension is 4194304 but corresponding boolean dimension is 65536定位到导致错误的代码,是metric.py,Collect values for Confusion Matrix 收集混淆矩阵的值时出错 …...

Java 中String对象详解
Java语言中的String对象是一个非常常见的数据类型,大多数情况下我们都是在使用String对象来表示字符串类型的数据。Java中的String类是一个final class,它是不可被继承的。本文将对Java中的String对象进行详细全面的描述,包括以下几个方面&am…...
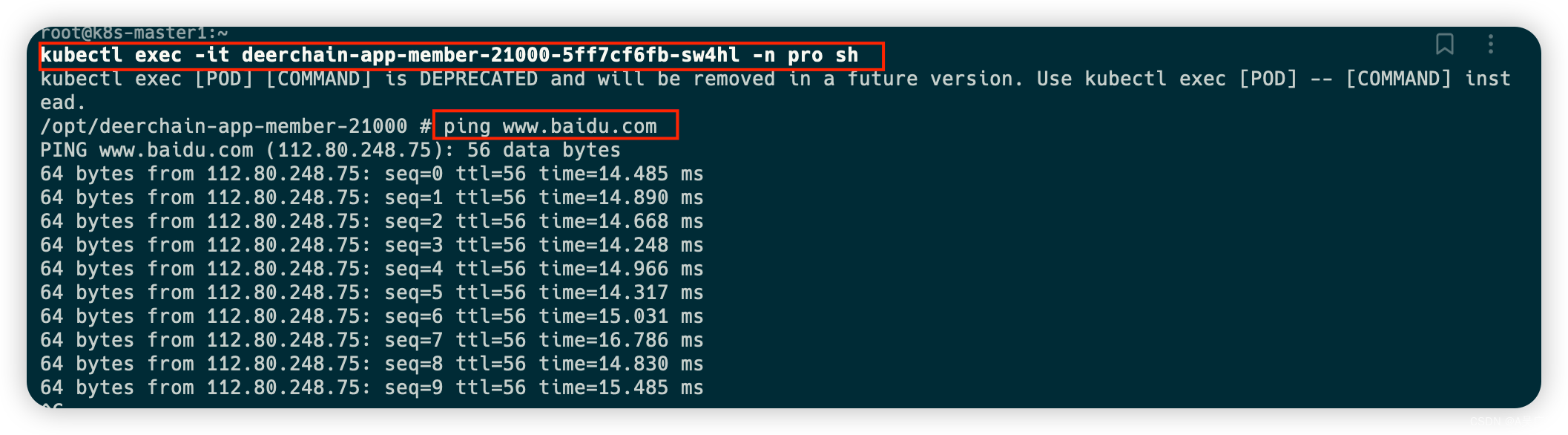
k8s nfs运行问题、etcd问题、calico网络问题
服务器重启后nfs运行问题导致服务不能正常重启 解决办法 在每个节点下使用如下命令进行查看nfs是否正常启动 systemctl status nfs 如果没有启动,则使用如下命令启动,保证三个节点下的nfs都正常启动 systemctl start nfs 再次查看nfs是否正常启动 syst…...

Qt--QString字符串类、QTimer定时器类
目录 1. QString 字符串类 dialog.cpp 2. 容器类 2.1 顺序容器 QList 示例代码: student.h student.cpp dialog.h dialog.cpp 运行结果: 2.2 关联容器 QMap 示例代码: dialog.h dialog.cpp 运行结果: 3. Qt类型 3.1 跨平台数据类型…...
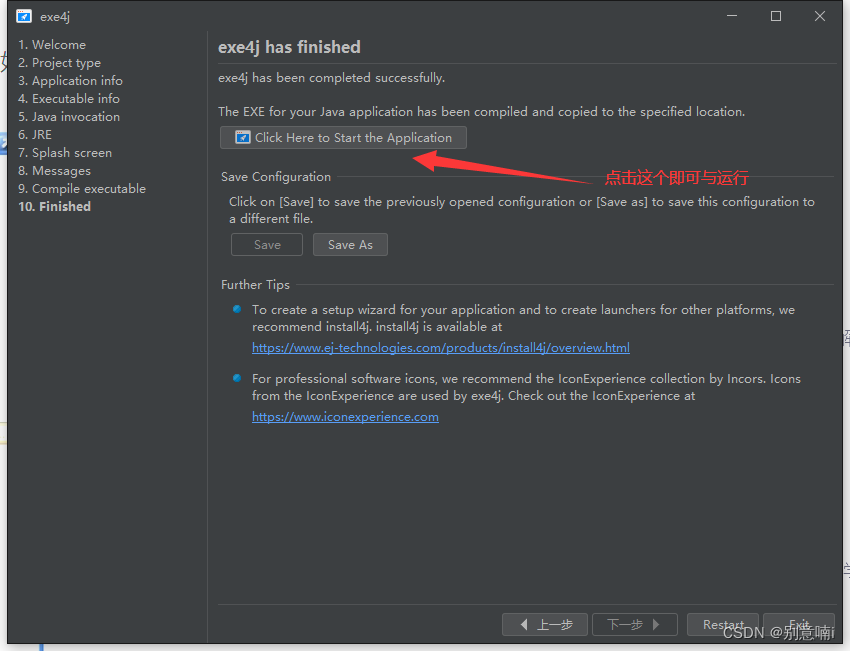
2023.5.13>>Eclipse+exe4j打包Java项目及获取exe所在文件的路径
Eclipseexe4j打包Java项目及获取exe所在文件的路径 1、打包exe文件1.1 打jar包1.2 打包exe2、在程序中获取exe所在路径3、遇到问题4、JDK version和class file version(Class编译版本号)对应关系5、参考文章 1、打包exe文件 1.1 打jar包 右单击项目选择“Export…” 1.2…...

Centos系统的使用基本教程
Centos是一款流行的Linux操作系统,它基于Red Hat Enterprise Linux系统,是一款稳定、可靠、安全的操作系统。本文将介绍Centos系统的基本使用方法,包括安装、命令行操作、软件安装和系统管理等方面的内容。 安装Centos系统 Centos系统可以从…...

IDEA生成ER图、UML类图、时序图、流程图等的插件推荐或独立工具推荐
以下是几个常用的IDEA插件和独立工具,可以用于生成ER图、UML类图、时序图、流程图等: Visual Paradigm (独立工具) Visual Paradigm是一个强大的建模工具,可以生成UML类图、时序图、流程图等。它支持多种语言和框架,包括Java、Spr…...

Python心经(3)
这一节总结点demo和常用知识点 目录 有关字符串格式化打印的 lambda匿名函数,,将匿名函数作为参数传入 文件读写 生成器 python的装饰器 简单的网站代码: 有关三元运算 推导式: 新浪面试题: 有关面向对象里…...

单工,半双工,全双工通讯
对于点对点之间的通信,按照消息传送的方向与时间关系,通信方式可分为单工通信、半双工通信及全双工通信三种。 单工通信 单工通信(Simplex Communication)是指消息只能单方向传输的工作方式。 在单工通信中,通信的信…...
)
【2023-05-09】 设计模式(单例,工厂)
2023-05-09 设计模式(单例,工厂) 单例模式 顾名思义,就是整个系统对外提供的实例有且只有一个 特点: 1、单例类只有一个实例 2、必须是自己创建唯一实例 3、必须给所以对象提供这个实例 分类ÿ…...
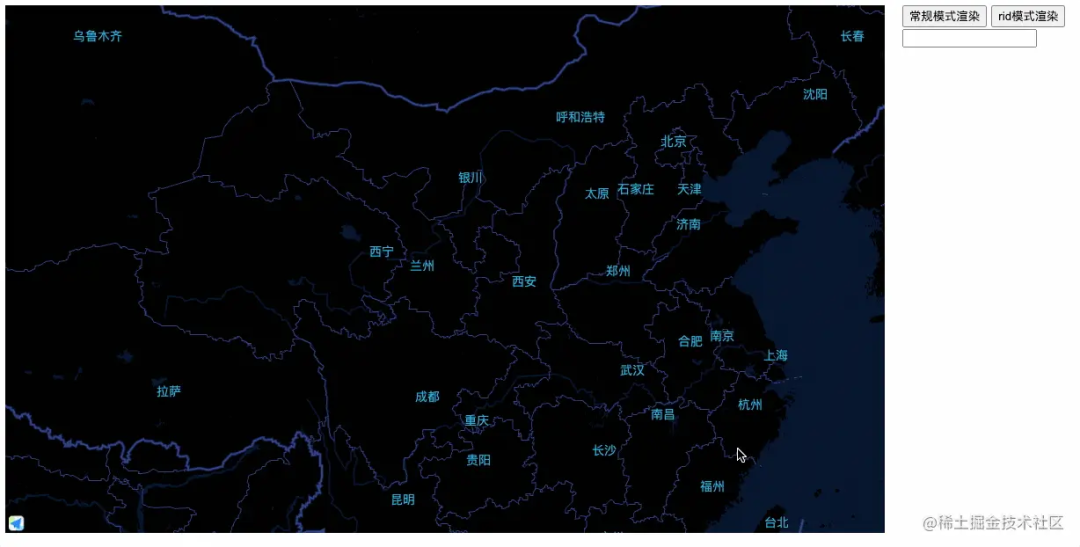
批量任务导致页面卡死解决方案
需求背景 需要基于高德地图展示海量点位(大概几万个),点位样式要自定义(创建DOM),虽然使用了聚合点,但初始化时仍需要将几万个点位的DOM结构都创建出来。 这里补充一句,高德地图在2.…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
