FPGA实现Cordic算法求解arctan和sqr(x*2 + y* 2)
一. 简介
由于在项目中需要使用的MPU6050,进行姿态解算,计算中设计到**arctan 和 sqr(x2 + y 2),**这两部分的计算,在了解了一番之后,发现Cordic算法可以很方便的一次性求出这两个这两部分的计算。另外也可以一次性求出sin和cos的值。另外该算法还可以计算其他的一些公式(没做过多的了解)。
二. Cordic算法
该算法的核心实现就是旋转逼近,每次旋转一定的角度,无限的逼近所给定的角度值。
1. 理论基础
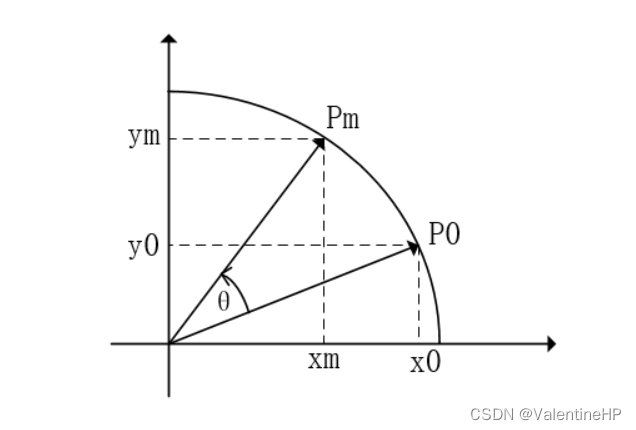
首先有向量P0,现在要将其旋转θ角度,到Pm。 那么Pm的坐标值如下
xm = x0cosθ - y0sinθ = cosθ(x0 – y0tanθ)
ym = x0sinθ + y0cosθ = cosθ(y0 + x0tanθ)
P0和Pm均在单位圆上,另外假设现在P0在X轴上,即 X0 = 1,y0 = 0。上式就可以变为如下显示
xm = x0cosθ - y0sinθ = cosθ
ym = x0sinθ + y0cosθ = sinθ
可以看到Pm的坐标值,就是sinθ 和 cosθ的值。这就是理论基础。
2. sinθ 和 cosθ 算法实现
有了理论支持后,我们只需要求解Pm的坐标即可。直接旋转θ不太可能,但是我们可以每次旋转特定的角度θi (tanθi = 1/2^i),让我们的角度值逼近θ即可。于是就有了如下迭代公式。
x(i+1) = cosθi* (xi – yi * tanθi)
y(i+1) = cosθi * (yi + xi * tanθi)
θ(i+1) = θi (±) dθi
如果当前角度小于设定角度,那么就加dθ ,大于设定角度 , 那么就减dθ。由于每次旋转的dθ,会越来越小,所以旋转的当前角度会越来越来接近设定角度。
计算过程中 ,cosθi,只充当缩放因子,对旋转方向没有影响。可以先在软件中提取技术出来。每次旋转角度值如下。

3. arctan (x,y)和 sqr(x*2 + y * 2)算法实现
在求解sinθ 和 cosθ 的时候,知道,给定一个角度,按照上述方法就可以求解。现在将其反过来,给定sinθ 和 cosθ的值,也就是Pm的坐标(可能不在单位圆上,只是模值缩放了),现在只需要将其旋转到X轴的正半轴上,即Y = 0 ,X > 0的时候,所旋转过的角度值即arctan (x,y)。
然后P0的X坐标值即sqr(x2 + y * 2)。旋转过程中,向量的模值是不会改变的,而Pm的模值就是sqr(x2 + y * 2)。
三. Cordic算法实现
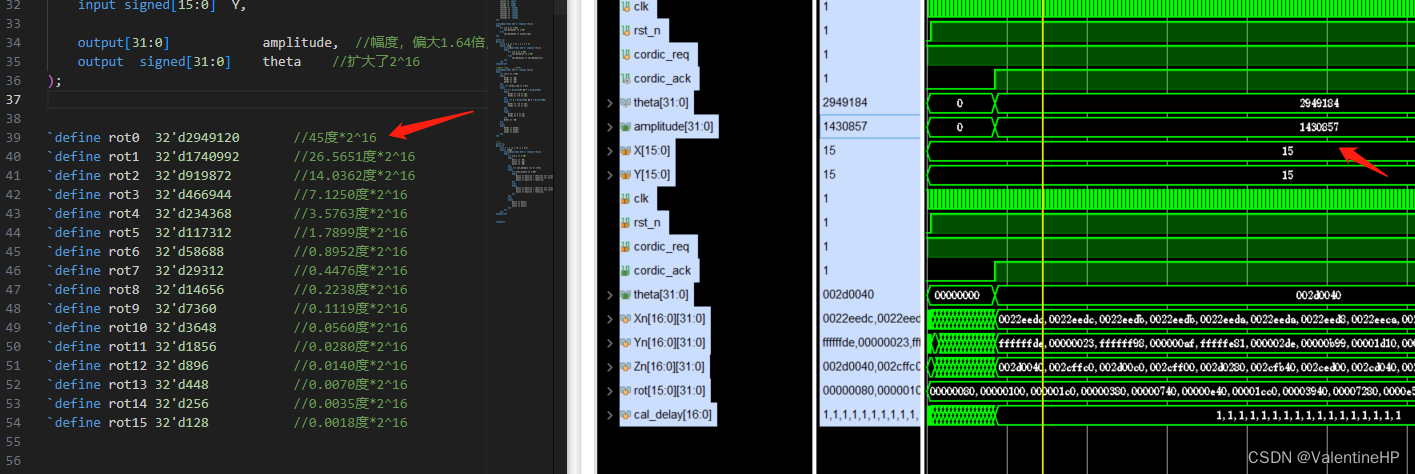
首先将上述角度值,存储到verilog中,需要进行扩大处理。由于tanθi = 1/2^i),所以对应的tanθ也是知道的。在相乘的时候,只需要将对应的数右移对应的位数即可
`define rot0 32'd2949120 //45度*2^16
`define rot1 32'd1740992 //26.5651度*2^16
`define rot2 32'd919872 //14.0362度*2^16
`define rot3 32'd466944 //7.1250度*2^16
`define rot4 32'd234368 //3.5763度*2^16
`define rot5 32'd117312 //1.7899度*2^16
`define rot6 32'd58688 //0.8952度*2^16
`define rot7 32'd29312 //0.4476度*2^16
`define rot8 32'd14656 //0.2238度*2^16
`define rot9 32'd7360 //0.1119度*2^16
`define rot10 32'd3648 //0.0560度*2^16
`define rot11 32'd1856 //0.0280度*2^16
`define rot12 32'd896 //0.0140度*2^16
`define rot13 32'd448 //0.0070度*2^16
`define rot14 32'd256 //0.0035度*2^16
`define rot15 32'd128 //0.0018度*2^16
然后就是迭代过程了,迭代16次足够了。最后的Zn和Xn就是想要结果。
//旋转
genvar i;
generatefor( i = 1 ;i < 17 ;i = i+1)begin: loop2always@(posedge clk or negedge rst_n)beginif( rst_n == 1'b0)beginXn[i] <= 'd0;Yn[i] <= 'd0;Zn[i] <= 'd0;endelse if( cal_delay[i -1] == 1'b1)beginif( Yn[i-1][31] == 1'b0)beginXn[i] <= Xn[i-1] + (Yn[i-1] >>> (i-1));Yn[i] <= Yn[i-1] - (Xn[i-1] >>> (i-1));Zn[i] <= Zn[i-1] + rot[i-1];endelsebeginXn[i] <= Xn[i-1] - (Yn[i-1] >>> (i-1));Yn[i] <= Yn[i-1] + (Xn[i-1] >>> (i-1));Zn[i] <= Zn[i-1] - rot[i-1];endendelsebeginXn[i] <= Xn[i];Yn[i] <= Yn[i];Zn[i] <= Zn[i];endendend
endgenerate
这里没有乘cosθ,最后的Xn会比真实值大1.64倍左右,所以还需要对其进行一个缩小操作,通过右移来近似实现。
assign cordic_ack = cal_delay[16];
assign theta = Zn[16];
assign amplitude = (Xn[16] >>> 1) + (Xn[16] >>> 3); 幅度,偏大1.64倍,这里做了近似处理
然后就是仿真了,给了X=Y=15,也就是角度为45度,幅值21.213,扩大65536倍为1,376,256。可以看到结果近似。
需要完整文件的可以关注公众号 FPGA之旅,私聊。后面等MPU6050的姿态解算模块完成了再完整上传。
相关文章:

FPGA实现Cordic算法求解arctan和sqr(x*2 + y* 2)
一. 简介 由于在项目中需要使用的MPU6050,进行姿态解算,计算中设计到**arctan 和 sqr(x2 y 2),**这两部分的计算,在了解了一番之后,发现Cordic算法可以很方便的一次性求出这两个这两部分的计算。另外也可以一次性求出sin和cos的…...

【最终截稿 | Springer 独立出版 | EI稳定检索】 2023年绿色建筑国际会议(ICoGB 2023)
会议简介 Brief Introduction 2023年绿色建筑国际会议(ICoGB 2023) 会议时间:2023年5月21日-23日 召开地点:瑞典斯德哥尔摩 大会官网:www.icogb.org ICoGB 2023将围绕“绿色建筑”的最新研究领域而展开,为研究人员、工程师、专家学…...

Flutter常用状态管理框架及优缺点
Flutter 中常见的状态管理框架有以下几种: Provider: Provider 是一个轻量级的状态管理框架,可用于单个 Widget 或整个 Widget 树中分发状态。它通过 InheritedWidget 和 ChangeNotifier 来实现状态管理,并支持依赖项注入。Redux…...
Ubuntu 20.04 系统配置 OpenVINO 2022.3 环境
由于 OpenVINO 2021 版本在调用 IECore 时会出现 Segmentation fault 的问题,因此需要将其升级为 2022 版本的。 1. 卸载原来版本的 OpenVINO 进入OpenVINO的卸载目录,通常在 /opt/intel 文件夹下, cd /opt/intel/openvino_2021/openvino_…...

浏览器存储技术:localStorage、sessionStorage和cookie的区别
随着互联网技术的不断发展,人们越来越依赖浏览器进行网页浏览和数据处理。浏览器存储技术是Web开发中非常重要的一部分,它可以帮助我们在浏览器端存储数据,而无需将数据传输到服务器。本文将介绍三种常见的浏览器存储技术:localSt…...

MySQL中的内连接和外连接
一、MySQL内连接(INNER JOIN) 内连接,又称为等值连接,是最常见的连接类型。它根据两个(或多个)表中具有相同列值的行来创建一个新的结果表。在内连接中,只有通过连接条件匹配的行才会被包含在结…...

node学习手册
Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行时,使 JavaScript 可以脱离浏览器环境运行在服务端。它提供了一组 API,可以让开发者轻松地进行服务器端编程。 以下是 Node.js 的学习手册: 安装 Node.js 首先,需要在官网…...

Java中的JSP是什么?如何实现JSP
JavaServer Pages(JSP)是一种Java技术,可以用于开发动态Web应用程序。它允许开发人员将Java代码嵌入到HTML页面中,以便生成动态内容。本文将介绍JSP的工作原理,以及如何在Java中实现JSP。 JSP的工作原理 JSP的工作原…...
c++之函数对象和谓词
目录 函数对象: 谓词: 一元谓词函数举例如下 二元谓词举例如下 函数对象和函数的区别 一元谓词的案例 二元函数对象案例 二元谓词案例 函数对象: 重载函数调用操作符的类,其对象常称为函数对象(function obj…...
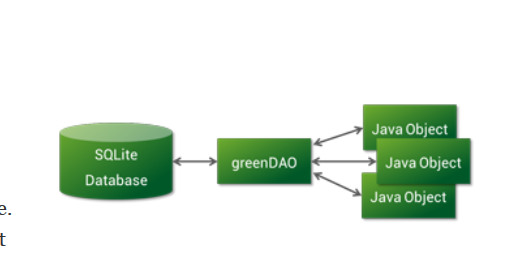
《Andorid开源》greenDao 数据库orm框架
一 前言:以前没用框架写Andorid的Sqlite的时候就是用SQLiteDatabase ,SQLiteOpenHelper ,SQL语句等一些东西,特别在写SQL语句来进行 数据库操作的时候是一件很繁琐的事情,有时候没有错误提示的,很难找到错误的地方&a…...
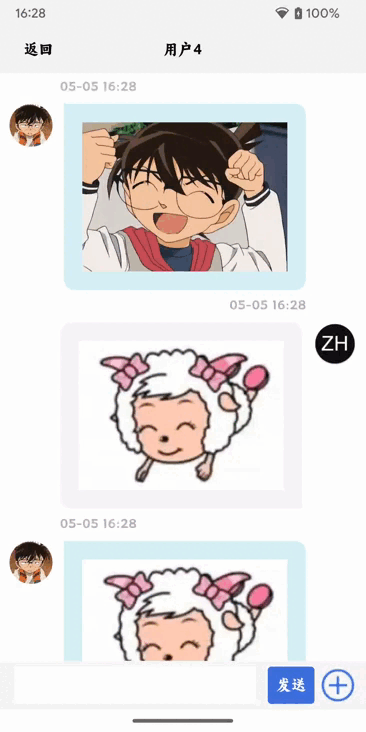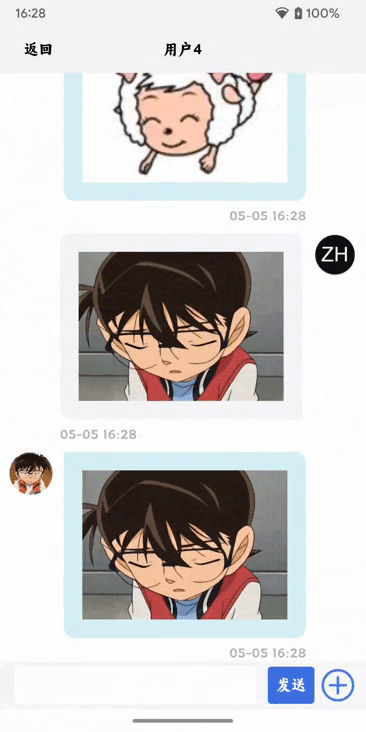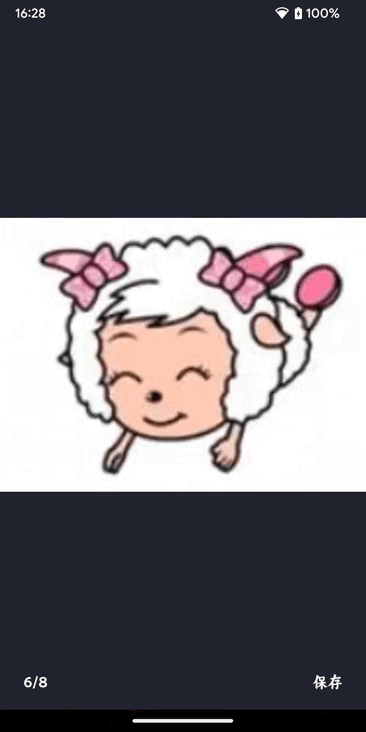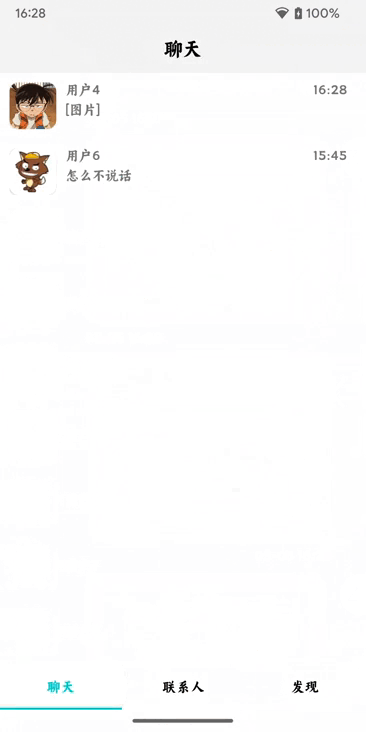
Android类似微信聊天页面教程(Kotlin)五——选择发送图片
前提条件 安装并配置好Android Studio Android Studio Electric Eel | 2022.1.1 Patch 2 Build #AI-221.6008.13.2211.9619390, built on February 17, 2023 Runtime version: 11.0.150-b2043.56-9505619 amd64 VM: OpenJDK 64-Bit Server VM by JetBrains s.r.o. Windows 11 …...

MongoDB:Win/Linux环境安装及一键部署脚本
1. Win安装 1.1 下载 MongoDB 安装程序 访问 MongoDB 官网,进入下载页面:Download MongoDB Community Server | MongoDB 选择 Windows 平台并下载最新版的 MongoDB 安装程序。 1.2 安装 MongoDB 双击安装程序,按照提示完成 MongoDB 的安装…...

KingbaseES V8R3 集群运维系列 -- failover切换后集群自动恢复
案例说明: KingbaseES V8R3集群默认在触发failover切换后,为保证数据安全,原主库需要通过人工介入后,恢复为新的备库加入到集群。在无人值守的现场环境,需要在触发failover切换后,主库可以自动恢复为新备…...
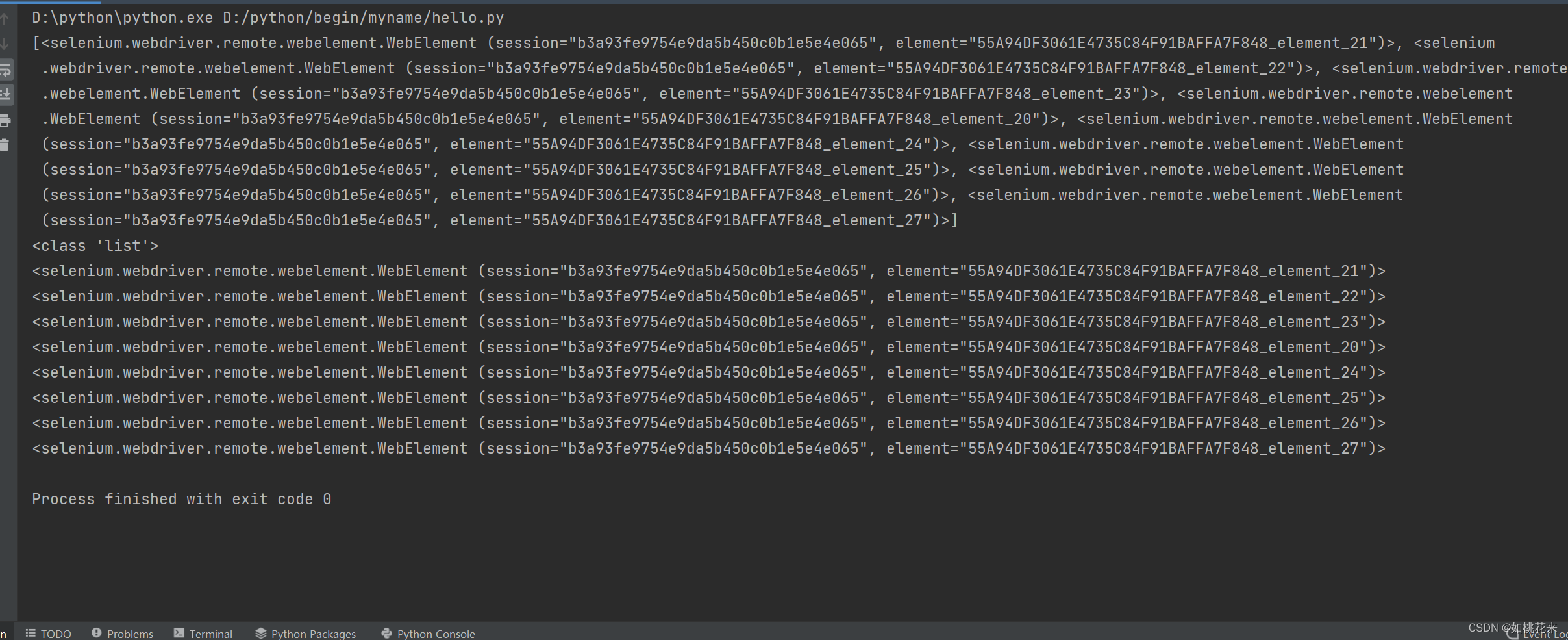
【Selenium中】——全栈开发——如桃花来
目录索引 查找元素:查找方法:单个元素查找:多个元素查找:*代码演示:* 元素交互操作:清空文字: 推荐的变量名定义名称:执行JavaScript :滚动页面方法:*滚动到底…...

Sarsa增强版之Sarsa-λ依然走迷宫
Sarsa-λ(Sarsa Lambda)是Sarsa算法的一种变体,其中“λ”表示一个介于0和1之间的参数,用于平衡当前状态和之前所有状态的重要性。 Sarsa算法是一种基于Q-learning算法的增量式学习方法,通过在实际环境中不断探索和学…...

生成 Cypher 能力:MOSS VS ChatGLM
生成 Cypher 能力:MOSS VS ChatGLM 生成 Cypher 能力:MOSS VS ChatGLM一、 测试结果二、 测试代码(包含Prompt) Here’s the table of contents: 生成 Cypher 能力:MOSS VS ChatGLM MOSS介绍:MOSS 是复旦大…...

数据库的键和存储
主键:数据库表中对存储数据对象给予以唯一和完整表示的数据列或属性的组合。一个数据列只能有一个主键,且主键的取值不能缺失,即不能为空。 外键:在一个表中存在另一个表得主键称此为表的外键。 为什么用自增列作为主键? 如果我们定义了主…...
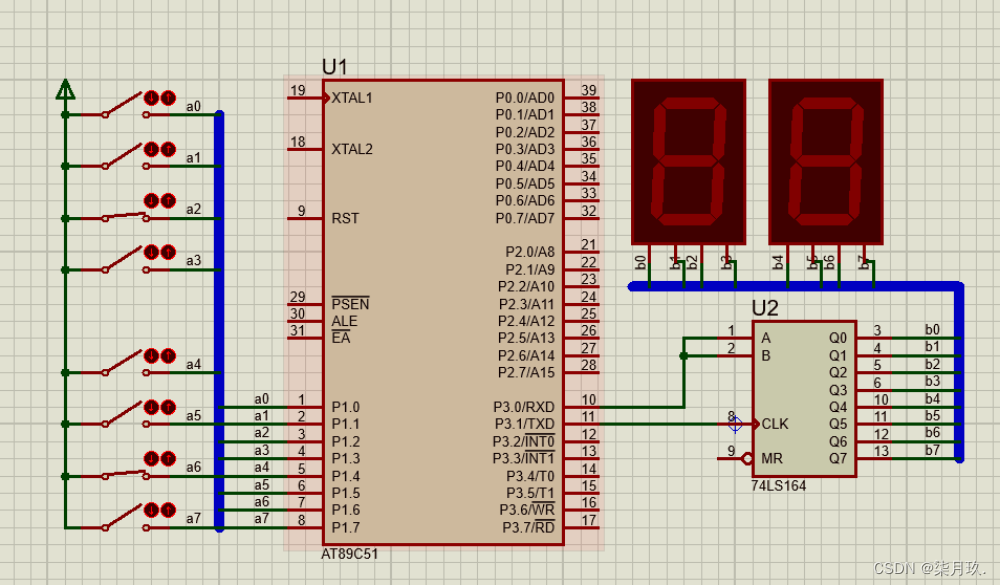
基于AT89C51单片机的并入串出乘法口诀的设计与仿真
点击链接获取Keil源码与Project Backups仿真图: https://download.csdn.net/download/qq_64505944/87779146?spm1001.2014.3001.5503 源码获取 并入串出乘法口诀的设计与仿真系统设计 目录 第一章 概述 3 1.1课题研究及意义 3 1.2课题设计内容 4 第二章系统设计…...

人生在世皆有过错,来一起看看Java中的异常吧!!!
Java中的异常问题详解 一、异常的概念与分类 1.异常概念 概念:Java异常是一个描述在代码段中发生异常的对象,当发生异常情况时,一个代表该异常的对象被创建并且在导致该异常的方法中被抛出,而该方法可以选择自己处理异常或者传…...

linux 测试连接网络和端口 telnet
一、安装telnet 1、检测telnet-server的rpm包是否安装 [rootlocalhost ~]# rpm -qa telnet-server 若无输入内容,则表示没有安装。出于安全考虑telnet-server.rpm是默认没有安装的,而telnet的客户端是标配。即下面的软件是默认安装的。 2、若未安装&…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
