【Leetcode】241. 为运算表达式设计优先级
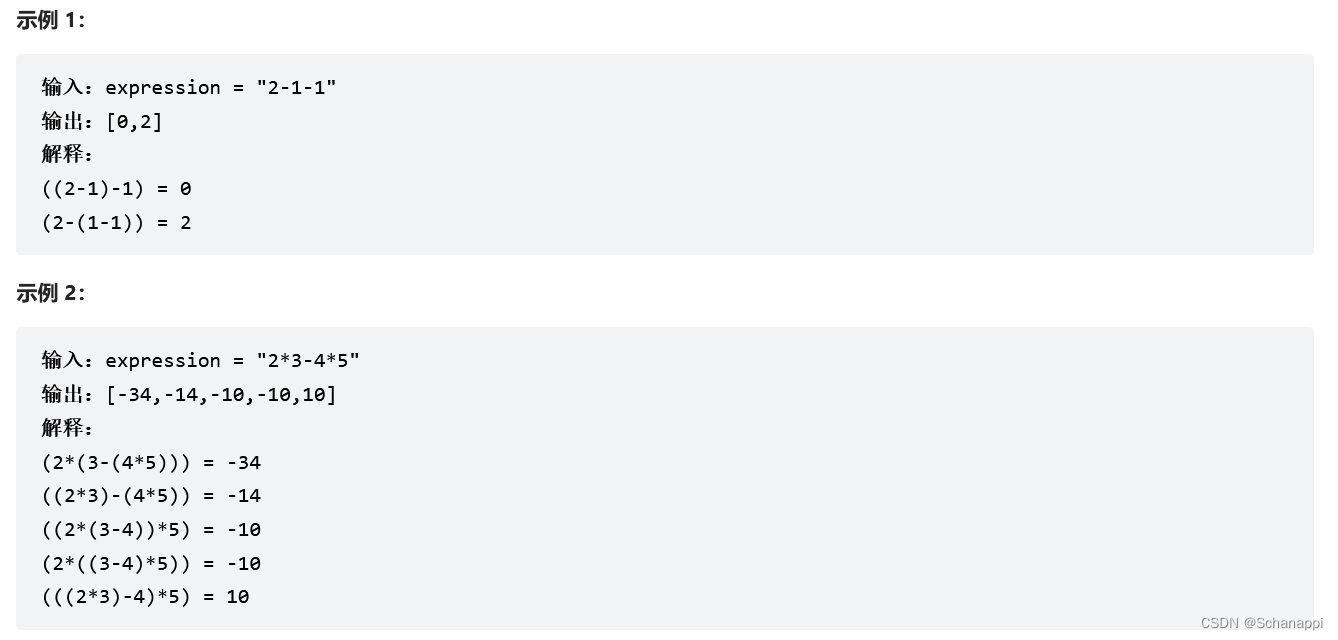
241. 为运算表达式设计优先级(中等)


解法一:分治法
对于这道题,加括号其实就是决定运算次序,所以我们可以把加括号转化为,「对于每个运算符号,先执行处理两侧的数学表达式,再处理此运算符号」。
对于一个形如 x op y 的算式而言,它的结果组合取决于 x 和 y 的结果组合数 ,而 x 和 y 又可以写成形如 x op y 的算式。
因此,该问题的子问题就是 x op y 中的 x 和 y:以运算符分隔的左右两侧算式解 。
对于分治算法分成三步走:
- 分解:按照运算符分隔成左右两部分,分别求解;
- 解决:通过递归实现,最终我们会得到只包含数字的算式,返回数字作为算式解;
- 合并:根据运算符合并左右两部分的解,得出最终解。
代码
class Solution {
public:vector<int> diffWaysToCompute(string expression) {vector<int> ans, left, right;int flag = 0; int n = expression.size();for(int i=0; i<n; ++i){// 如果 expression[i] 是运算符号if(!isdigit(expression[i])){flag = 1; // flag=1说明string是表达式,flag=0说明string是一个数字// string s(str, begin, len):// 将字符串str中从下标begin开始、长度为len的部分作为字符串初值left = diffWaysToCompute(string(expression, 0, i));right = diffWaysToCompute(string(expression, i+1, n-i));// 遍历left和right的所有结果数for(int l : left){for(int r : right){if(expression[i] == '+') ans.push_back(l + r);if(expression[i] == '-') ans.push_back(l - r);if(expression[i] == '*') ans.push_back(l * r);}}}}if(flag == 0){// expression 只是一个数字// {int} -> vector<int>return {stoi(expression)};}return ans;}
};
解法二:分治法+记忆化
解法一中存在重复运算,比如 2*3 - 4*5 ,按照第一个 * 分割,右边部分是 3 - 4*5 ,进而计算 4*5 ,而按照 - 分割,同样会再次计算 4*5 。
为了减少重复运算,可以使用记忆化搜索,保存字符串区间[l,r]的运算结果,整个思路和解法一类似,不同点在于:设置一个 map 保存结果,递归的时候先在 map 中查找,如果该字符串已经计算过,那么直接返回保存的结果。
代码
class Solution {
public:unordered_map<string, vector<int>> mp;vector<int> diffWaysToCompute(string expression) {if(mp.find(expression) != mp.end()) return mp.find(expression) -> second;vector<int> ans, left, right;int flag = 0; int n = expression.size();for(int i=0; i<n; ++i){// 如果 expression[i] 是运算符号if(!isdigit(expression[i])){flag = 1; // flag=1说明string是表达式,flag=0说明string是一个数字// string s(str, begin, len):// 将字符串str中从下标begin开始、长度为len的部分作为字符串初值left = diffWaysToCompute(string(expression, 0, i));right = diffWaysToCompute(string(expression, i+1, n-i));// 遍历left和right的所有结果数for(int l : left){for(int r : right){if(expression[i] == '+') ans.push_back(l + r);if(expression[i] == '-') ans.push_back(l - r);if(expression[i] == '*') ans.push_back(l * r);}}}}if(flag == 0){// expression 只是一个数字// {int} -> vector<int>return {stoi(expression)};}mp[expression] = ans;return ans;}
};
解法三:动态规划
对于表达式 expression 需要做预处理:「把每个数字转为 int 存起来,同时运算符也存起来」。
这样子将得到两个数组,以 2 * 3 - 4 * 5 为例,存起来的数字是 numList = [2 3 4 5],存起来的运算符是 opList = [*, -, *]。
状态定义
dp[i][j] 表示从第 i 个数字到第 j 个数字(从 0 开始计数)范围内表达式的所有解。
如 dp[1][3]表示:第 1 个数字 (3) 到 第 3 个数字(5)范围内表达式 3 - 4 * 5 的所有解。
状态转移方程
有了一个数字的所有解(初始化),就可以求出两个数字的所有解。
有了两个数字的所有解,三个数字的所有解就和解法一求法一样。
把三个数字分成两部分,将两部分的解两两组合起来即可。
对于两部分之间的运算符,因为表达式是一个数字一个运算符,所以运算符的下标就是左部分最后一个数字的下标。
对于 2 * 3 - 4 * 5 ,存起来的数字是 numList = [2 3 4 5], 存起来的运算符是 opList = [*, -, *]。
假设要求 dp[1][3],也就是计算 3 - 4 * 5 的解:
-
分成 3 和 4 * 5 两部分,3 对应的下标是 1 ,对应的运算符就是
opList[1] = '-',也就是计算3 - 20 = -17; -
分成 3 - 4 和 5 两部分,4 的下标是 2 ,对应的运算符就是
opList[2] = '*'。
也就是计算-1 * 5 = -5 -
所以
dp[1][3] = [-17 -5]。
四个、五个… 都可以分成两部分,然后通过之前的解求出来。
直到包含了所有数字的解求出来。
初始化
对范围内只有一个数字的情况进行初始化:
dp[0][0] = 2, dp[1][1] = 3, dp[2][2] = 4, dp[3][3] = 5;
返回的最终结果
最终返回第 0 个数字到最后一个数字范围内表达式的所有解,即 dp[0][n-1];
代码
class Solution {
public:vector<int> diffWaysToCompute(string expression) {vector<int> numList;vector<char> opList;// 对 expression 预处理int num = 0;for(char ch : expression){if(!isdigit(ch)){numList.push_back(num);num = 0;opList.push_back(ch);}else{num = num * 10 + ch - '0';}}numList.push_back(num);int n = numList.size();vector<vector<vector<int>>> dp(n, vector<vector<int>>(n));// dp数组初始化for(int i=0; i<n; ++i){dp[i][i].push_back(numList[i]);}// 从2个数字遍历到n个数字for(int k=2; k<=n; ++k){// 开始遍历的下标for(int i=0; i<n; ++i){// 结束遍历的下标int j = i + k - 1;if(j >= n){// 越界break;}vector<int> ans;// 以s作为分隔点分成左右两部分遍历for(int s=i; s<j; ++s){vector<int> left = dp[i][s];vector<int> right = dp[s+1][j];// 遍历左边部分的所有结果值for(auto x : left){// 遍历右边部分的所有结果值for(auto y : right){// 根据操作符对所有结果进行组合// 操作符下标就是左边部分最后一个数字的下标char op = opList[s];if(op == '+') ans.push_back(x + y);else if(op == '-') ans.push_back(x - y);else if(op == '*') ans.push_back(x * y);}}}dp[i][j] = ans;}}return dp[0][n-1];}
};
相关文章:

【Leetcode】241. 为运算表达式设计优先级
241. 为运算表达式设计优先级(中等) 解法一:分治法 对于这道题,加括号其实就是决定运算次序,所以我们可以把加括号转化为,「对于每个运算符号,先执行处理两侧的数学表达式,再处理此…...

torch两个向量除法,对于分母向量中的元素为0是设置为1,避免运算错误
在gpu运行时,如果在进行两个向量除法的时候,对于分母向量中的元素为0是设置为1,避免运算错误。 可以使用torch的division函数以及clamp函数来解决这个问题。具体步骤如下: 使用division函数将分子向量除以分母向量。 使用clamp函…...

NodeJs 最近各版本特性汇总
(预测未来最好的方法就是把它创造出来——尼葛洛庞帝) NodeJs 官方链接 github链接 V8链接 Node.js发布于2009年5月,由Ryan Dahl开发,是一个基于Chrome V8引擎的JavaScript运行环境,使用了一个事件驱动、非阻塞式I/O模…...

python数据分析案例——天猫订单综合分析
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 什么是数据分析 明确目的–获得数据(爬虫,现有,公开的数据)–数据预处理——数据可视化——结论 准备 环境使用: 在开始写我们的代码之前,我们要准备好运行代码的程序 Anacon…...
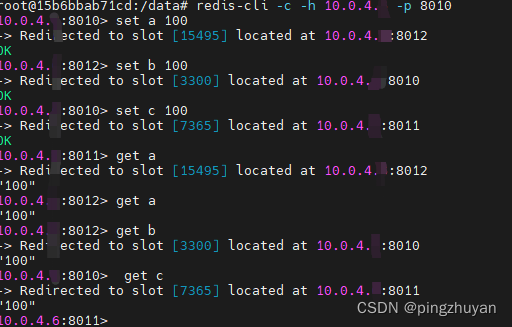
05- redis集群模式搭建(上) (包含云服务器[填坑])
目录 1. 准备环境: 2. 简介: -> 2.1 前言: -> 2.2 Redis集群架构实现了对redis的水平扩容 -> 2.3 redis cluster集群原理 3. 搭建后特别需要注意的问题 ->3.1 [重点]: 如果一个服务出现故障: 是否可以继续提供服务??? ---> 3.1.1 如果集群中故障re…...

【AI】YOLOV1原理详解
AI学习目录汇总 0、前言 YOLOv1~3作者是约瑟夫雷德蒙(Joseph Chet Redmon),他的网站:https://pjreddie.com/ YOLOv1网站:https://pjreddie.com/darknet/yolov1/ YOLOv2网站:https://pjreddie.com/darknet…...
提高APP安全性的必备加固手段——深度解析代码混淆技术
APP 加固方式 Android APP 加固是优化 APK 安全性的一种方法,常见的加固方式有混淆代码、加壳、数据加密、动态加载等。下面介绍一下 Android APP 加固的具体实现方式。 混淆代码: 使用 ProGuard 工具可以对代码进行混淆,使得反编译出来的代…...

想让行车记录仪协助道路病害自动化检测?可以!
针对【RGB3DS道路表观病害信息智慧检测系统】,我们着重介绍过其与道路检测车做集成预装或者处理道路检测车数据的极大便利,其中之一便是可高效输出带有道路检测车桩号标记的病害报表,这是因为道路检测车数据本身具有规范性。 那么如果使用道…...
git上传大大大文件项目好折磨人
本来想把unity项目的源码上传上gitee啊,但是那个项目有1个多G,还是个半成品,要是写完,都不知道行不行 正常的上传 所用到的命令: 1、 git init 初始化,创建本地仓库 2、 git add . 添加到本地仓库 3、 git…...

java常见异常的处理方法
以下是一些常见的异常处理方法: 捕获和处理异常(try-catch): 使用try-catch语句块可以捕获并处理异常。在try块中编写可能抛出异常的代码,然后在catch块中指定异常类型,以便捕获并处理异常。 try {// 可能抛…...

上传图片到阿里云服务器base64 上传
//上传图片到阿里云服务器 function upload_Ali($remoteImage){$imageData $this->n_img_base_64($remoteImage);if ($imageData ! false) {// 初始化 cURL 句柄$ch curl_init();// 设置请求 URL 和一些 cURL 选项curl_setopt($ch, CURLOPT_URL, http://dev.com/index/aja…...

【致敬未来的攻城狮计划】— 连续打卡第二十六天:瑞萨RA Cortex-M 内核RA2E1 RT-Thread BSP 启蒙知识
系列文章目录 由于一些特殊原因: 系列文章链接:(其他系列文章,请点击链接,可以跳转到其他系列文章)或者参考我的专栏“ 瑞萨MCU ”,里面是 瑞萨RA2E1 系列文章。 24.RA2E1的 DMAC——数据传输 …...
)
2023年5月8日-5月14日(方案C,下班UE视频教程为主)
目前,ue视频教程进行到了智 慧 城 市(3.13),mysql(7.1),tf1(4.11),蓝图反射(1.9),moba(1.5)webapp(2.4),mmoarpg(00A_04),fps1_12(0:3…...

「MIAOYUN」:降本增效,赋能传统企业数字化云原生转型 | 36kr 项目精选
作为新经济综合服务平台第一品牌,36氪自2019年落地四川站以来,不断通过新锐、深度的商业报道,陪跑、支持四川的新经济产业。通过挖掘本土优质项目,36氪四川帮助企业链接更多资源,助力企业成长,促进行业发展…...

Python突破JS加密限制,进行逆向解密
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 目录标题 前言开发环境:模块使用:逆向目标逆向过程参数 JS 加密关键代码Python 登录关键代码尾语 💝 开发环境: Python 3.8 Pycharm 模块使用: time >>> 时间模块,属于内置,无…...

【Linux】exec函数族
目录 1、exec函数族的介绍2、exec相关函数 1、exec函数族的介绍 2、exec相关函数 #include <unistd.h> int execl(const char *pathname, const char *arg0, ... /* (char *)0 */ ); /* - path 需要指定的执行的文件的路径或者名称,相对路径or绝对路径- arg …...

OSQP二次规划求解库使用说明
OSQP二次规划求解库使用说明 贺志国 2023.5.10 1. 凸二次规划的一般表达式 m i n 1 2 x T P x q T x s . t . l ≤ A x ≤ u min \quad \frac{1}{2}x^T Px q^Tx \qquad s.t. \quad l \leq Ax \leq u min21xTPxqTxs.t.l≤Ax≤u 其中, P P P称为内核矩阵&#x…...

Elasticsearch(一)
Elasticsearch(一) 初始elasticsearch 什么是elasticsearch elasticsearch是一款非常强大的开源搜索引擎,可以帮助我们从海量数据中快速查找到需要的内容 elasticsearch结合kibana、Logstash、Beats,也就是elastic stack&…...

深入探究Java中的枚举类型:定义、特性和应用
引言: 在Java编程中,枚举类型是一种强大而灵活的工具,用于定义一组具名的常量。它不仅提供了代码可读性和可维护性的优势,还为开发人员提供了一种更安全和结构化的方式来处理固定的常量集合。本文将深入探讨Java中的枚举类型&…...

linux密码忘了?一招解决
目录 一、前言 二、进入编辑界面 三、单用户模式 四、修改密码 五、更新信息 六、退出 七、验证 一、前言 版本:centos7.9、VMware15.5 在我们学习linux运行级别的时候,面试题可能会出如何找回root密码,下面来详细的介绍一波ÿ…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
