Python(符号计算常微分方程)谐振子牛顿运动方程
牛顿运动方程
牛顿运动方程可以写成以下形式
F = d p d t = m d v d t = m d 2 r d t 2 \mathbf{F}=\frac{d \mathbf{p}}{d t}=m \frac{d \mathbf{v}}{d t}=m \frac{d^2 \mathbf{r}}{d t^2} F=dtdp=mdtdv=mdt2d2r
恒力问题
具有恒定力的问题意味着恒定的加速度。 典型的例子是一个在倾斜平面上滑动的块,其中质量为 m m m 的块同时受到重力和摩擦力的作用。 合力 F F F 由重力 F g F_g Fg 、法向力 N N N 和摩擦力 f f f_f ff 的矢量和给出
F = F g + N + f f = m a \mathbf{F}=\mathbf{F}_g+\mathbf{N}+\mathbf{f}_f=m \mathbf{a} F=Fg+N+ff=ma
线性恢复力
一类重要的问题是线性恢复力,服从胡克定律。这种情况下的运动方程是
F ( x ) = − k x = m x ¨ F(x)=-k x=m \ddot{x} F(x)=−kx=mx¨
符号计算谐振子牛顿运动方程
不考虑摩擦简单示例
让我们从一个简单的物理学原型微分方程开始:谐振子。 这个方程式出现在物理学的所有领域,不同的背景下:不仅是力学,还有电动力学、量子力学、固态物理学等等。 谐振子的牛顿运动方程为
x ¨ + ω 2 x = 0 \ddot{x}+\omega^2 x=0 x¨+ω2x=0
考虑摩擦示例
到目前为止,我们的谐振子是自由的,没有感觉到任何摩擦。我们将在常微分方程中添加一个与速度成正比的摩擦项:
x ¨ + 2 β x ˙ + ω 2 x = 0 \ddot{x}+2 \beta \dot{x}+\omega^2 x=0 x¨+2βx˙+ω2x=0
考虑驱动力和摩擦示例
当我们在常微分方程的右侧添加一项时,这对应于添加一个驱动力。具体来说,添加正弦力:
x ¨ + 2 β x ˙ + ω 2 x = F 0 sin ω 0 t \ddot{x}+2 \beta \dot{x}+\omega^2 x=F_0 \sin \omega_0 t x¨+2βx˙+ω2x=F0sinω0t
Python计算机代数源代码
参阅 - 亚图跨际
相关文章:
谐振子牛顿运动方程)
Python(符号计算常微分方程)谐振子牛顿运动方程
牛顿运动方程 牛顿运动方程可以写成以下形式 F d p d t m d v d t m d 2 r d t 2 \mathbf{F}\frac{d \mathbf{p}}{d t}m \frac{d \mathbf{v}}{d t}m \frac{d^2 \mathbf{r}}{d t^2} Fdtdpmdtdvmdt2d2r 恒力问题 具有恒定力的问题意味着恒定的加速度。 典型的例子是…...
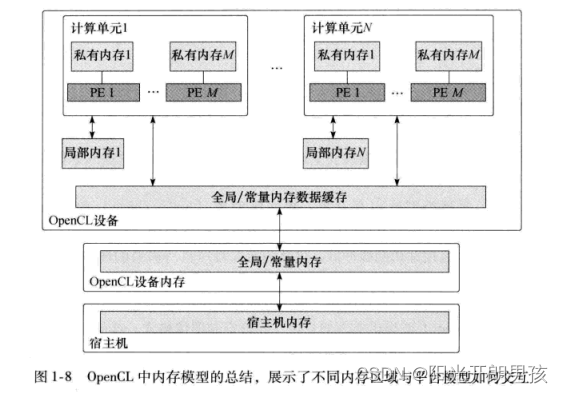
OpenCL编程指南-1.2OpenCL基本概念
OpenCL概念基础 面向异构平台的应用都必须完成以下步骤: 1)发现构成异构系统的组件。 2)探查这些组件的特征,使软件能够适应不同硬件单元的特定特性。 3)创建将在平台上运行的指令块(内核)。 4)…...

使用 ChatGPT 辅助学习——为自己找一个老师
我们每个人都有许多标签,例如高中生、成绩中等、文科,根据这些标签我和其他拥有相同标签的人分配了相同的教程、班级和老师,这可以带来效率上的提升,因为同一份教程、老师就可以服务几十上百人,而无须为每个人定制&…...
用户与权限管理)
MySQL基础(二十一)用户与权限管理
1. 用户管理 1.1 登录MySQL服务器 启动MySQL服务后,可以通过mysql命令来登录MySQL服务器,命令如下: mysql –h hostname|hostIP –P port –u username –p DatabaseName –e "SQL语句"-h参数后面接主机名或者主机IP,…...

程序员的下一个风口
面对近一年的裁员潮,以及 GPT 出现带来的 AI 颠覆潮流,各种话题出现:「前端已死」、「后端已死」、「Copy/Paste 程序员将被 AI 取代」。程序员行业是否还有发展空间? 这一两年的就业机会是因为经济衰落周期内造成的,不…...

Android 自定义View 之 简易输入框
简易输入框 前言正文① 构造方法② XML样式③ 测量④ 绘制1. 绘制方框2. 绘制文字 ⑤ 输入1. 键盘布局2. 键盘接口3. 键盘弹窗4. 显示键盘5. 相关API 四、使用自定义View五、源码 前言 在日常工作开发中,我们时长会遇到各种各样的需求,不部分需求是可以通…...

SpringMVC的基础知识
创建SpringMVC项目 SpringMVC项目其实和SpingBoot项目差不多,就多引入了一个SpringWeb项目而已拉 可以看这篇博客,创建的就是一个SpringMVC项目--创建项目の博客 SpringMVC是啥 Spring是啥相信大家都了解 啥是MVC呢?MVC是Model View Controller的缩写 我们分开看这三个词Model…...

OpenPCDet系列 | 4.2 DataAugmentor点云数据增强模块解析
文章目录 DataAugmentor模块解析1. gt_sampling2. random_world_flip3. random_world_rotation4. random_world_scaling5. limit_period DataAugmentor模块解析 在pointpillars算法中,具体的数据增强方法配置是在yaml中的DATA_CONFIG.DATA_AUGMENTOR进行配置&#…...

精准测试之过程与实践 | 京东云技术团队
作者:京东工业 宛煜昕 一、怎样的技术 •百度百科: 精准测试是一套计算机测试辅助分析系统。 精准测试的核心组件包含的软件测试示波器、用例和代码的双向追溯、智能回归测试用例选取、覆盖率分析、缺陷定位、测试用例聚类分析、测试用例自动生成系统…...
类ChatGPT逐行代码解读(1/2):从零实现Transformer、ChatGLM-6B
前言 最近一直在做类ChatGPT项目的部署 微调,关注比较多的是两个:一个LLaMA,一个ChatGLM,会发现有不少模型是基于这两个模型去做微调的,说到微调,那具体怎么微调呢,因此又详细了解了一下微调代…...
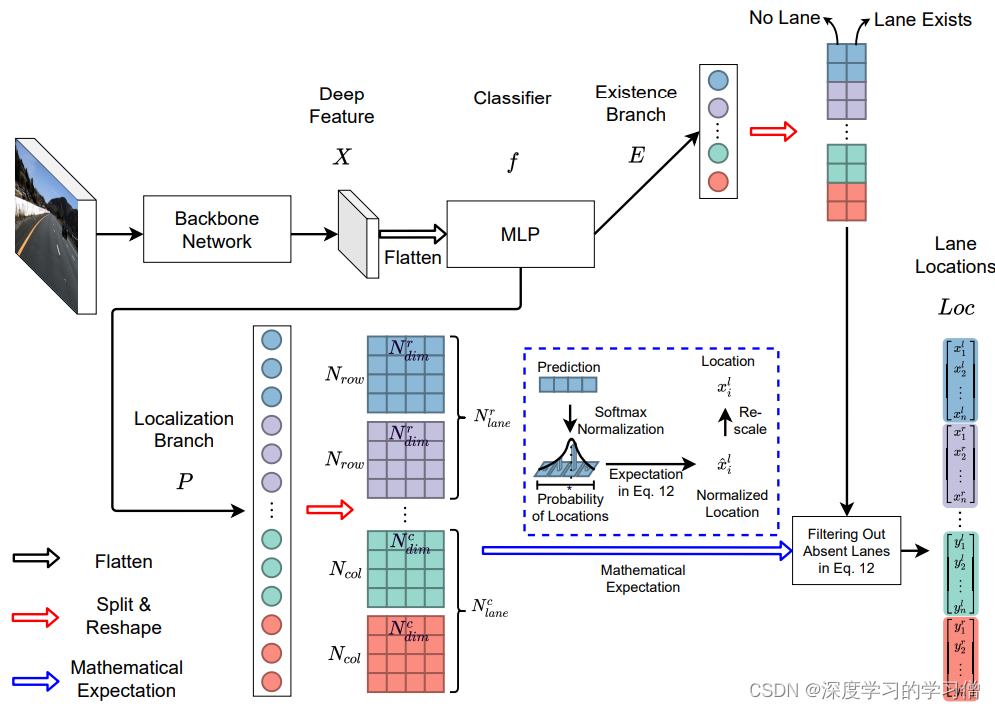
车道线检测
前言 目前,车道线检测技术已经相当成熟,主要应用在自动驾驶、智能交通等领域。下面列举一些当下最流行的车道线检测方法: 基于图像处理的车道线检测方法。该方法是通过图像处理技术从摄像头传回的图像中提取车道线信息的一种方法,…...

云渲染靠谱吗,使用云渲染会不会被盗作品?
云渲染靠谱吗、安全吗?如果使用 云渲染会不会被盗作品......Renderbus瑞云渲染作为一个正经的云渲染平台,也时不时会收到这类疑问,首先,瑞云渲染是肯定靠谱的,各位可以放心使用。另外小编也将在本篇教你如何辨别云渲染平台是否安全…...
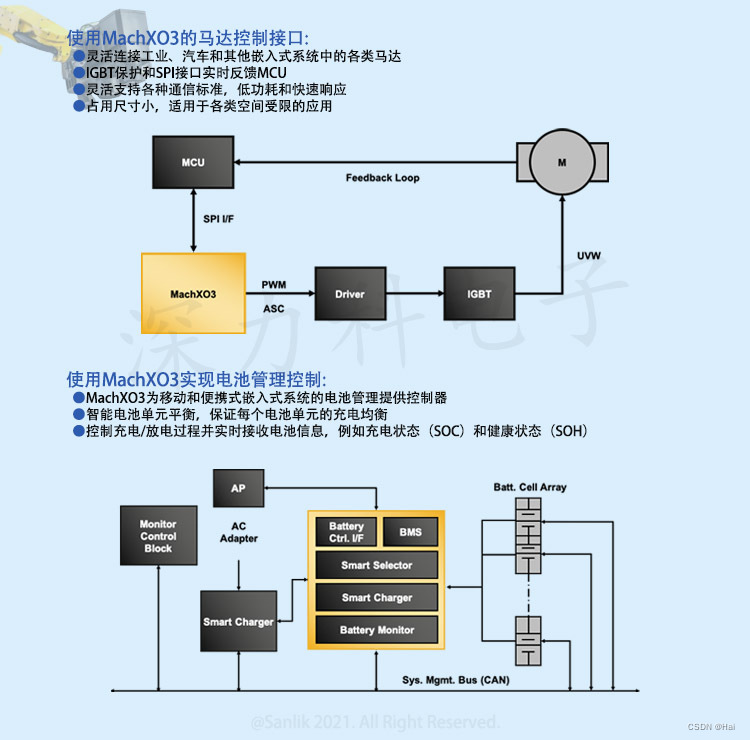
什么是FPGA?关于FPGA基础知识 一起来了解FPGA lattice 深力科 MachXO3系列 LCMXO3LF-9400C-5BG256C
什么是FPGA?关于FPGA基础知识 一起来了解FPGA lattice 深力科 MachXO3系列 LCMXO3LF-9400C-5BG256C FPGA基础知识:FPGA是英文Field-Programmable Gate Array的缩写,即现场可编程门阵列,它是在PAL、GAL、CPLD等可编程器…...

有什么好用的云渲染?
在CG制作流程中,离线渲染一直是必要且耗时的环节。你的场景越复杂,渲染出现问题的可能性就越大,尤其是当你独自工作,没有人给你建议的时候,灯光、模型、场景任何一个环节渲染时出现问题都可能让你焦头烂额,…...
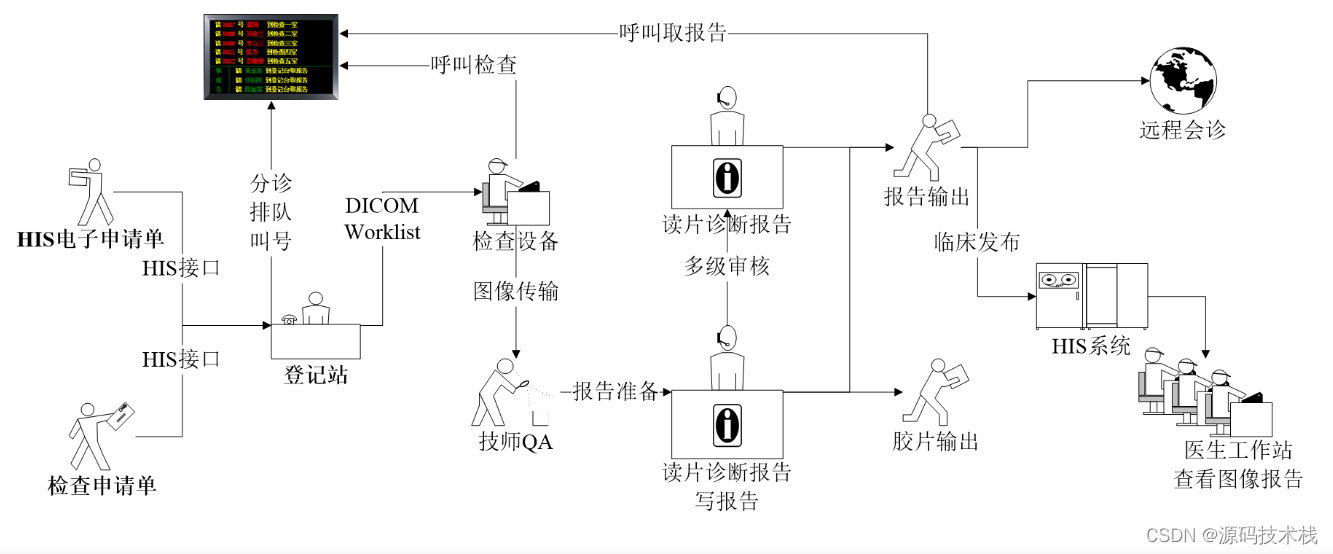
什么是医学影像PACS系统?PACS系统功能有哪些?作用有哪些?对接哪些设备?业务流程是什么?
一、什么是医学影像PACS系统 PACS:为Picture Archive and CommunicationSystem的缩写,是图象归档和通讯系统。PACS系统应用在医院影像科室的系统,主要的任务就是把日常产生的各种医学影像(包括核磁,CT,超声…...

分布式缓存:什么是它以及为什么需要它?
前言 随着网络的快速发展,分布式应用变得越来越普遍。这种类型的应用程序需要访问多个组件和服务,而这些组件可能分散在不同的物理位置上。在这种情况下,由于网络通信的高延迟和低带宽,性能问题变得尤为明显。为解决这一问题&…...
MySQL基础(二十二)逻辑架构
1.逻辑架构剖析 1.1 第1层:连接层 系统(客户端)访问MySQL服务器前,做的第一件事就是建立TCP连接。 经过三次握手建立连接成功后,MySQL服务器对TCP传输过来的账号密码做身份认证、权限获取。 用户名或密码不对&#…...

《Kubernetes证书篇:使用TLS bootstrapping简化kubelet证书制作》
一、背景 Master apiserver启用TLS认证后,Node节点kubelet和kube-proxy要与kube-apiserver进行通信,必须使用CA签发的有效证书才可以,当Node节点很多时,这种客户端证书颁发需要大量工作,同样也会增加集群扩展复杂度。 …...

vue+elementui+nodejs机票航空飞机航班查询与推荐
语言 node.js 框架:Express 前端:Vue.js 数据库:mysql 数据库工具:Navicat 开发软件:VScode )本系统主要是为旅客提供更为便利的机票预定方式,同时提高民航的预定机票的工作效率。通过网络平台实现信息化和网络化&am…...

将ssh发布密钥添加到服务器的ssh授权密钥中,但是为什么我仍然无法ssh登录到此服务器?
我已经将ssh发布密钥添加到服务器的ssh授权密钥中,但是为什么我仍然无法ssh登录到此服务器? 即使将ssh公钥添加到服务器的授权密钥中,您也可能无法通过SSH登录到服务器,这有几个原因: 1.服务器的authorized_keys文件的权限不正确…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
