实验二十、压控电压源二阶 LPF 幅频特性的研究
一、题目
研究压控电压源二阶低通滤波电路品质因数 Q Q Q 对频率特性的影响。
二、仿真电路
电路如图1所示。集成运放采用 LM324AJ,其电源电压为 ±15V。

图 1 压控电压源二阶低通滤波电路幅频特性的测试 图1\,\,压控电压源二阶低通滤波电路幅频特性的测试 图1压控电压源二阶低通滤波电路幅频特性的测试
三、仿真内容
分别测量 R f = 10 k Ω R_f=10\,\textrm kΩ Rf=10kΩ、 15 k Ω 15\,\textrm kΩ 15kΩ 时的幅频特性,测量通带电压增益以及 f = f 0 f=f_0 f=f0 处的电压增益。
四、仿真结果
仿真结果如表1所示。(将波特图仪显示屏上的指针移至曲线平坦的位置就可测量到通带电压增益) 表 1 压控电压源二阶低通滤波器幅频特性的测试结果 表1\,\,压控电压源二阶低通滤波器幅频特性的测试结果 表1压控电压源二阶低通滤波器幅频特性的测试结果
| 反馈电阻 | 特征频率 | 通带电压增益 | 通带电压放大倍数 | f = f 0 f=f_0 f=f0 处的电压增益 | f = f 0 f=f_0 f=f0 处的电压放大倍数 | 品质因数 |
|---|---|---|---|---|---|---|
| R f R_f Rf/kΩ | f 0 f_0 f0/Hz | 20 lg ∣ A ˙ u p ∣ 20\lg|\dot A_{up}| 20lg∣A˙up∣/dB | A ˙ u p \dot A_{up} A˙up | 20 lg ∣ A ˙ u ∣ f = f 0 ∣ 20\lg|\dot A_u|_{f=f_{0}}| 20lg∣A˙u∣f=f0∣/dB | A ˙ u ∣ f = f 0 \dot A_u\big|_{f=f_0} A˙u f=f0 | Q = ∣ A ˙ u ∣ f = f 0 A ˙ u p ∣ Q=\Big|\displaystyle\frac{\dot A_u|_{f=f_0}}{\dot A_{up}}\Big| Q= A˙upA˙u∣f=f0 |
| 10 | 1000 | 6.02 | 2 | 5.814 | 1.95 | 0.975 |
| 15 | 1000 | 7.959 | 2.5 | 13.785 | 4.89 | 1.956 |
五、结论
反馈电阻 R f R_f Rf 增大,通带电压放大倍数 A ˙ u p \dot A_{up} A˙up 增大,从而使 f = f 0 f=f_0 f=f0 处的电压放大倍数增大。适当调节 A ˙ u p \dot A_{up} A˙up 增大品质因数 Q Q Q,可以改善滤波电路的频率特性。当通带电压放大倍数 A ˙ u p \dot A_{up} A˙up 分别为 2 和 2.5 时,计算得到的 Q Q Q 值分别为 1 和 2,与实验结果近似。
相关文章:

实验二十、压控电压源二阶 LPF 幅频特性的研究
一、题目 研究压控电压源二阶低通滤波电路品质因数 Q Q Q 对频率特性的影响。 二、仿真电路 电路如图1所示。集成运放采用 LM324AJ,其电源电压为 15V。 图 1 压控电压源二阶低通滤波电路幅频特性的测试 图1\,\,压控电压源二阶低通滤波电路幅频特性的测试 图1压控…...
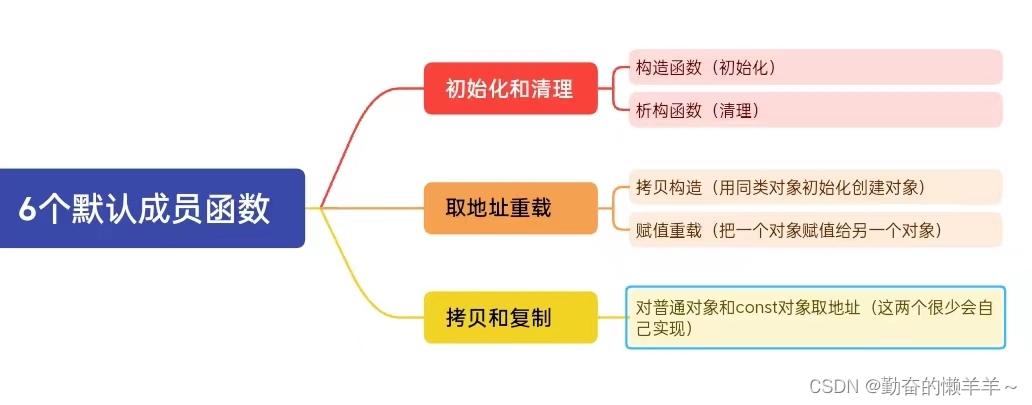
类和对象【C++】【中篇】
目录 一、类的6个默认成员函数 1、构造函数 2、析构函数 3、拷贝构造函数 4、赋值重载函数 二、赋值运算符重载 一、类的6个默认成员函数 注意:默认成员函数不能在类外面定义成全局函数。因为类里没有的话会自动生成,就会产生冲突。 1、构造函数…...

2.SpringBoot运维实用篇
SpringBoot运维实用篇 基础篇发布以后,看到了很多小伙伴在网上的留言,也帮助超过100位小伙伴解决了一些遇到的问题,并且已经发现了部分问题具有典型性,预计将有些问题在后面篇章的合适位置添加到本套课程中,作为解…...

【c++】浅讲引用
【c】浅讲引用 前言引用定义作用做输出型参数引用作返回值总结 关于引用的权限 结尾 前言 博主开始细学c和linux了 这次就带来浅学了的引用。 引用 定义 引用不是在内存中开辟一个新空间的新变量 类似于给变量取别名,和取别名的对象在空间中公用一个对象 例&#…...
)
CSS布局基础(文字[行内<块>]与行内[块]垂直对齐方式 文字溢出显示省略号)
文字[行内<块>]与行内[块]垂直对齐方式 文字[行内<块>]与行内[块]垂直对齐方式概述图片底部空隙问题 文字溢出显示省略号单行文字多行文字 文字[行内<块>]与行内[块]垂直对齐方式 概述 vertical-align: top | middle| bottom | baseline(默认) | sub | sup…...
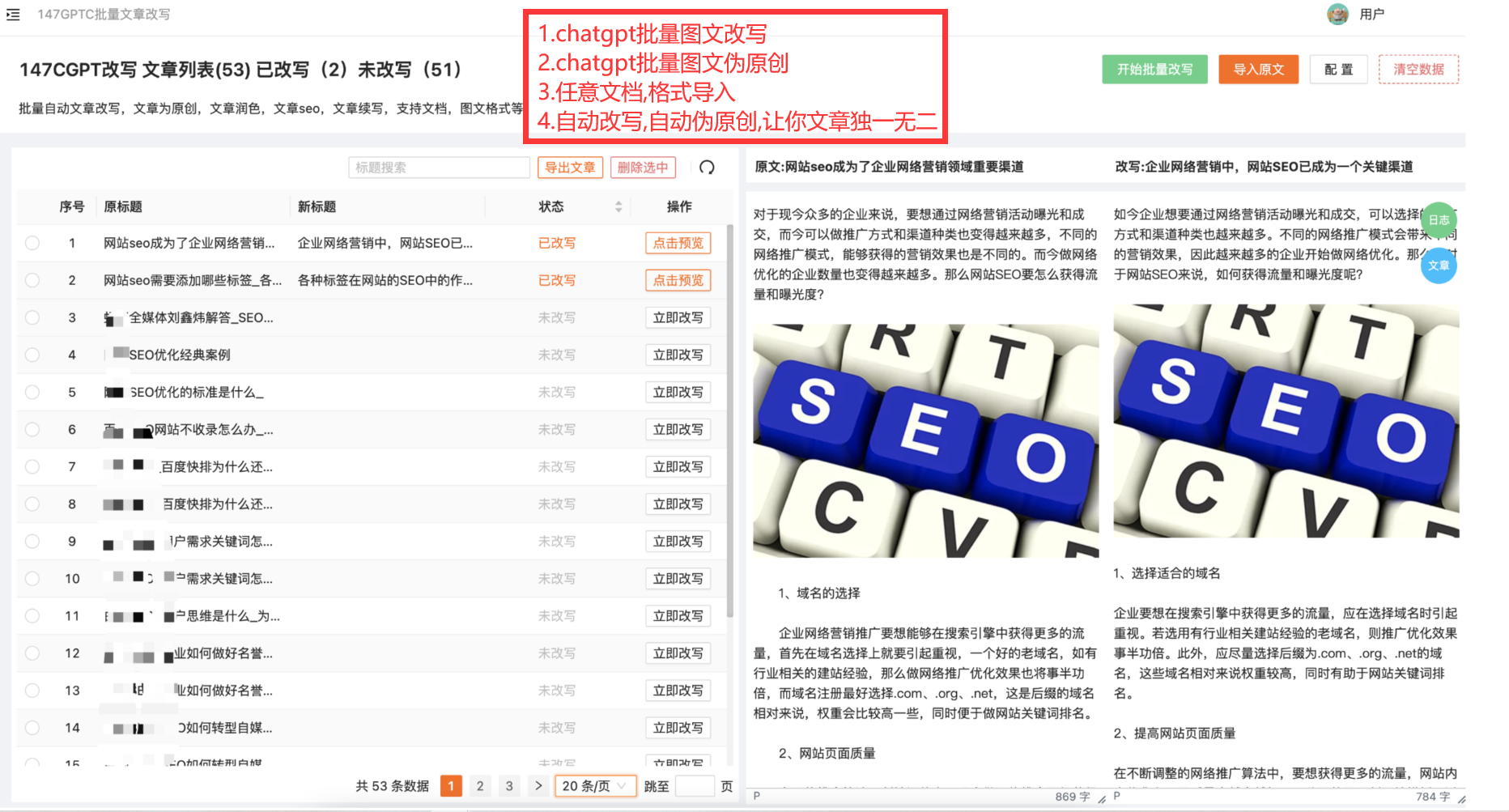
AI自动写文章_免费在线原创文章生成器
自动写文章生成器 自动写文章生成器是一种利用人工智能和自然语言处理技术,帮助用户快速生成文章的工具。该软件可以根据用户的需求和选择,自动生成符合要求的文章,无需手动编写和修改。 自动写文章生成器的主要功能包括以下几个方面&#…...

Java阶段二Day15
Java阶段二Day15 文章目录 Java阶段二Day15复习前日知识点对象数据类型注入数组类型注入集合类型的注入p命名空间引入外部属性文件 基于XML管理beanbean的作用域bean的生命周期代码演示生命周期后置处理器处理展示基于XML的自动装配 基于注解管理bean开启组件扫描使用注解定义B…...
从月薪3000到月薪20000,自动化测试应该这样学...
绝大多数测试工程师都是从功能测试做起的,工作忙忙碌碌,每天在各种业务需求学习和点点中度过,过了好多年发现自己还只是一个功能测试工程师。 随着移动互联网的发展,从业人员能力的整体进步,软件测试需要具备的能力要…...

Python魔法方法 单例模式
前言 本文介绍一下python中常用的魔法方法以及面向对象中非常重要的单例模式。 魔法方法 python中一切皆对象,因为python是面向对象的编程语言。python给类和对象提供了大量的内置方法,这些内置方法也称魔法方法。这些魔法方法总是在某种条件下自动触…...

计算机网络基础知识(三)—— 什么是OSI七层模型?
文章目录 00 | 🛸发展史🛸01 | 🛸OSI七层参考模型🛸02 | 🛸OSI七层参考模型的信息流向🛸 OSI七层模型是Open Systems Interconnection Reference Model的缩写,是由国际标准化组织(IS…...
谐振子牛顿运动方程)
Python(符号计算常微分方程)谐振子牛顿运动方程
牛顿运动方程 牛顿运动方程可以写成以下形式 F d p d t m d v d t m d 2 r d t 2 \mathbf{F}\frac{d \mathbf{p}}{d t}m \frac{d \mathbf{v}}{d t}m \frac{d^2 \mathbf{r}}{d t^2} Fdtdpmdtdvmdt2d2r 恒力问题 具有恒定力的问题意味着恒定的加速度。 典型的例子是…...
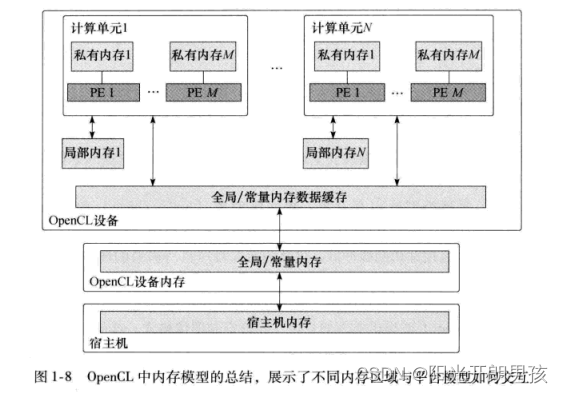
OpenCL编程指南-1.2OpenCL基本概念
OpenCL概念基础 面向异构平台的应用都必须完成以下步骤: 1)发现构成异构系统的组件。 2)探查这些组件的特征,使软件能够适应不同硬件单元的特定特性。 3)创建将在平台上运行的指令块(内核)。 4)…...

使用 ChatGPT 辅助学习——为自己找一个老师
我们每个人都有许多标签,例如高中生、成绩中等、文科,根据这些标签我和其他拥有相同标签的人分配了相同的教程、班级和老师,这可以带来效率上的提升,因为同一份教程、老师就可以服务几十上百人,而无须为每个人定制&…...
用户与权限管理)
MySQL基础(二十一)用户与权限管理
1. 用户管理 1.1 登录MySQL服务器 启动MySQL服务后,可以通过mysql命令来登录MySQL服务器,命令如下: mysql –h hostname|hostIP –P port –u username –p DatabaseName –e "SQL语句"-h参数后面接主机名或者主机IP,…...

程序员的下一个风口
面对近一年的裁员潮,以及 GPT 出现带来的 AI 颠覆潮流,各种话题出现:「前端已死」、「后端已死」、「Copy/Paste 程序员将被 AI 取代」。程序员行业是否还有发展空间? 这一两年的就业机会是因为经济衰落周期内造成的,不…...

Android 自定义View 之 简易输入框
简易输入框 前言正文① 构造方法② XML样式③ 测量④ 绘制1. 绘制方框2. 绘制文字 ⑤ 输入1. 键盘布局2. 键盘接口3. 键盘弹窗4. 显示键盘5. 相关API 四、使用自定义View五、源码 前言 在日常工作开发中,我们时长会遇到各种各样的需求,不部分需求是可以通…...

SpringMVC的基础知识
创建SpringMVC项目 SpringMVC项目其实和SpingBoot项目差不多,就多引入了一个SpringWeb项目而已拉 可以看这篇博客,创建的就是一个SpringMVC项目--创建项目の博客 SpringMVC是啥 Spring是啥相信大家都了解 啥是MVC呢?MVC是Model View Controller的缩写 我们分开看这三个词Model…...

OpenPCDet系列 | 4.2 DataAugmentor点云数据增强模块解析
文章目录 DataAugmentor模块解析1. gt_sampling2. random_world_flip3. random_world_rotation4. random_world_scaling5. limit_period DataAugmentor模块解析 在pointpillars算法中,具体的数据增强方法配置是在yaml中的DATA_CONFIG.DATA_AUGMENTOR进行配置&#…...

精准测试之过程与实践 | 京东云技术团队
作者:京东工业 宛煜昕 一、怎样的技术 •百度百科: 精准测试是一套计算机测试辅助分析系统。 精准测试的核心组件包含的软件测试示波器、用例和代码的双向追溯、智能回归测试用例选取、覆盖率分析、缺陷定位、测试用例聚类分析、测试用例自动生成系统…...
类ChatGPT逐行代码解读(1/2):从零实现Transformer、ChatGLM-6B
前言 最近一直在做类ChatGPT项目的部署 微调,关注比较多的是两个:一个LLaMA,一个ChatGLM,会发现有不少模型是基于这两个模型去做微调的,说到微调,那具体怎么微调呢,因此又详细了解了一下微调代…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
