(邱维声)高等代数课程笔记:基,维数与坐标
3.5 基,维数与坐标
\quad 本节,继续研究线性空间的结构。一般地,设 V V V 是数域 K K K 上的一个线性空间。
\quad 首先,我们先将“线性相关”与“线性无关”的概念由“有限”向“无限”推广。
对比其它高等代数教程,邱老师在这一节非常巧妙的将“有限维”与“无限维”统一在了一起!
定义 1. 线性空间子集的线性相关与线性无关:
(1) V V V 的一个有限子集 { α 1 , α 2 , ⋯ , α s } \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{s}\} {α1,α2,⋯,αs} 线性相关 : ⟺ :\Longleftrightarrow :⟺ 向量组 α 1 , α 2 , ⋯ , α s \boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{s} α1,α2,⋯,αs 线性相关;
(2) V V V 的一个有限子集 { α 1 , α 2 , ⋯ , α s } \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{s}\} {α1,α2,⋯,αs} 线性无关 : ⟺ :\Longleftrightarrow :⟺ 向量组 α 1 , α 2 , ⋯ , α s \boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{s} α1,α2,⋯,αs 线性无关;
(3) V V V 的一个无限子集 S S S 线性相关 : ⟺ :\Longleftrightarrow :⟺ 存在 S S S 的一个有限子集线性相关;
(4) V V V 的一个无限子集 S S S 线性无关 : ⟺ :\Longleftrightarrow :⟺ S S S 的任一个有限子集都线性无关。
例 1:平面 π \pi π 上的任意两个不共面的向量可成为该平面的一个基。
定义 2. 极大线性无关集与基:设 V V V 是数域 K K K 上的一个线性空间。 V V V 的一个子集 S S S 如果满足:
(1) S S S 是线性无关的;
(2)对于 ∀ β ∈ V \ S \forall ~ \boldsymbol{\beta} \in V \backslash S ∀ β∈V\S(如果还有的话),有 S ∪ { β } S \cup \{\boldsymbol{\beta}\} S∪{β} 线性相关,
则称 S S S 为 V V V 的一个 极大线性无关集。
\quad 可以看到,“极大线性无关集”的概念以及与“基”相近了,不过我们需要排除一些意外情况,比如 V = { 0 } V =\{\boldsymbol{0}\} V={0}.
\quad 由 前一节 的讨论,我们知道 { 0 } \{\boldsymbol{0}\} {0} 是线性相关的,因此,若 V ≠ { 0 } V \ne \{\boldsymbol{0}\} V={0},则称 V V V 的一个极大线性无关集为 V V V 的一个 基。
\quad 如果将上述定义推广到 V = { 0 } V =\{\boldsymbol{0}\} V={0} 的情形,则需要做一些规定:空集 ϕ \phi ϕ 是线性无关的。之后再进行分析:若 V = { 0 } V =\{\boldsymbol{0}\} V={0},由于
(1) ϕ \phi ϕ 是线性无关的;
(2)对于 0 ∈ V \ ϕ \boldsymbol{0} \in V \backslash \phi 0∈V\ϕ,有 ϕ ∪ { 0 } = { 0 } \phi \cup \{\boldsymbol{0}\} = \{\boldsymbol{0}\} ϕ∪{0}={0} 线性相关,
由 定义 2, ϕ \phi ϕ 是 { 0 } \{\boldsymbol{0}\} {0} 的一个极大线性无关集,此时,我们称 ϕ \phi ϕ 是 V V V 的一个基。
- 简单来讲,若规定“空集是线性无关的”,则线性空间的一个极大线性无关集,就是其的一个基。
定义 2是合理的,但我们一般不会采用这个定义,因为这个定义比较抽象,不太直观。
定义 3. 基:设 V V V 是数域 K K K 上的一个线性空间。 V V V 的一个子集 S S S 若满足:
(1) S S S 是线性无关的;
(2) V V V 中的任一向量可由 S S S 中的有限多个向量线性表出,
则称 S S S 是 V V V 的一个 基。
\quad 另外,
(1)若 S = { α 1 , α 2 , ⋯ , α r } S = \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{r}\} S={α1,α2,⋯,αr}(即 S S S 为有限集),也称向量组 α 1 , α 2 , ⋯ , α r \boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{r} α1,α2,⋯,αr 是 V V V 的一个(有序)基;
(2)规定: ϕ \phi ϕ 是线性无关的;
(3)规定:线性空间 { 0 } \{\boldsymbol{0}\} {0} 的一个基是 ϕ \phi ϕ。
\quad 相较于
定义 2,在定义 3的基础上,只能规定"线性空间 { 0 } \{\boldsymbol{0}\} {0} 的一个基是 ϕ \phi ϕ",而由定义 2 是可以直接推出的。
\quad 现在思考一个问题:是否任一个线性空间都有基?答案是肯定的,详情请参见 高等代数——大学创新教材(下册) P 158 ∼ P 159 P_{158}\sim P_{159} P158∼P159。
定义 4. 有限维与无限维:
(1)若 V V V 有一个基是 V V V 的有限子集,则称 V V V 是 有限维的;
(2)若 V V V 有一个基是 V V V 的无限子集,则称 V V V 是 无限维的。
定理 1:若 V V V 是有限维的,则 V V V 的任意两个基所含个数相等。
证明:
\quad 一般地,设向量组 { α 1 , α 2 , ⋯ , α n } \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}\} {α1,α2,⋯,αn} 是 V V V 的一个基,任取 V V V 的另一个基 S S S,
(1)若 S S S 所含的向量个数 > n >n >n,则在 S S S 中至少可取 n + 1 n+1 n+1 个向量 β 1 , β 2 , ⋯ , β n + 1 \boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{n+1} β1,β2,⋯,βn+1。显然,向量组 { β 1 , β 2 , ⋯ , β n + 1 } \{\boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{n+1}\} {β1,β2,⋯,βn+1} 可由向量组 { α 1 , α 2 , ⋯ , α s } \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{s}\} {α1,α2,⋯,αs} 线性表出,由于 n + 1 > n n+1>n n+1>n,因此 β 1 , β 2 , ⋯ , β n + 1 \boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{n+1} β1,β2,⋯,βn+1 线性相关,从而产生矛盾。
(2)设 S S S 中所含向量的个数 ≤ n \le n ≤n,不妨设为 m m m。显然有
{ α 1 , α 2 , ⋯ , α n } ≅ { β 1 , β 2 , ⋯ , β m } , \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}\} \cong \{\boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\cdots,\boldsymbol{\beta}_{m}\}, {α1,α2,⋯,αn}≅{β1,β2,⋯,βm},
等价的线性无关的向量组所含向量的个数相等,因此 m = n m=n m=n.
#
推论:若 V V V 是无限维的,则 V V V 的任意一个基都是无限维的。
定义 5. 维数:
(1)若 V V V 是有限维的,则称 V V V 的一个基所含向量的个数为 V V V 的 维数。记作: dim V \dim V dimV。
(2)若 V V V 是无限维的,则将 V V V 的维数记作 dim V = ∞ \dim V = \infty dimV=∞。
(3)若 V = { 0 } V = \{\boldsymbol{0}\} V={0},则 dim V = 0 \dim V = 0 dimV=0。
命题 1:设 V V V 是 n n n 维的,则 V V V 中任意 n + 1 n+1 n+1 个向量都线性相关。
命题 2:设 dim V = n \dim V = n dimV=n, S = { α 1 , α 2 , ⋯ , α n } S = \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}\} S={α1,α2,⋯,αn} 是 V V V 的一个基,则 V V V 中任一向量 α = a 1 α 1 + ⋯ + a n α n \boldsymbol{\alpha} = a_{1} \boldsymbol{\alpha}_{1}+\cdots + a_{n} \boldsymbol{\alpha}_{n} α=a1α1+⋯+anαn 的表出方式唯一。
定义 6. 坐标:设 dim V = n \dim V = n dimV=n, { α 1 , α 2 , ⋯ , α n } \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}\} {α1,α2,⋯,αn} 是 V V V 的一个基,向量 α = a 1 α 1 + ⋯ + a n α n ∈ V \boldsymbol{\alpha} = a_{1} \boldsymbol{\alpha}_{1}+\cdots + a_{n} \boldsymbol{\alpha}_{n} \in V α=a1α1+⋯+anαn∈V,则称 α \boldsymbol{\alpha} α 的 坐标 为:
( a 1 a 2 ⋮ a n ) \left( \begin{array}{c} \boldsymbol{a}_1\\ \boldsymbol{a}_2\\ \vdots\\ \boldsymbol{a}_n\\ \end{array} \right) a1a2⋮an
命题 3:设 dim V = n \dim V = n dimV=n,则 V V V 中任意 n n n 个线性无关的向量都是 V V V 的一个基。
命题 4:设 dim V = n \dim V = n dimV=n,若 V V V 中任一向量可由向量组 α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n} α1,α2,⋯,αn 线性表出,则集合 { α 1 , α 2 , ⋯ , α n } \{\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}\} {α1,α2,⋯,αn} 是 V V V 的一个基。
命题 5:设 dim V = n \dim V = n dimV=n,则 V V V 的任意一个线性无关的向量组都能扩充成 V V V 的一个基。
命题 6:设 dim V = n \dim V = n dimV=n, W W W 是 V V V 的一个子空间,则 dim W ≤ dim V \dim W \le \dim V dimW≤dimV。
命题 7:向量组 α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n} α1,α2,⋯,αn 的一个极大线性无关组是 < α 1 , α 2 , ⋯ , α n > <\boldsymbol{\alpha}_{1},\boldsymbol{\alpha}_{2},\cdots,\boldsymbol{\alpha}_{n}> <α1,α2,⋯,αn> 的一个基。
命题 8:关于向量组的生成子空间,我们有:
( < α 1 , α 2 , ⋯ , α s > = < β 1 , β 2 , ⋯ , β t > ) ⟺ ( { α 1 , α 2 , ⋯ , α s } ≅ { β 1 , β 2 , ⋯ , β t } ) \left( <\boldsymbol{\alpha }_1,\boldsymbol{\alpha }_2,\cdots ,\boldsymbol{\alpha }_s>=<\boldsymbol{\beta }_1,\boldsymbol{\beta }_2,\cdots ,\boldsymbol{\beta }_t> \right) \,\,\Longleftrightarrow \left( \left\{ \boldsymbol{\alpha }_1,\boldsymbol{\alpha }_2,\cdots ,\boldsymbol{\alpha }_s \right\} \cong \left\{ \boldsymbol{\beta }_1,\boldsymbol{\beta }_2,\cdots ,\boldsymbol{\beta }_t \right\} \right) (<α1,α2,⋯,αs>=<β1,β2,⋯,βt>)⟺({α1,α2,⋯,αs}≅{β1,β2,⋯,βt})
相关文章:
高等代数课程笔记:基,维数与坐标)
(邱维声)高等代数课程笔记:基,维数与坐标
3.5 基,维数与坐标 \quad 本节,继续研究线性空间的结构。一般地,设 V V V 是数域 K K K 上的一个线性空间。 \quad 首先,我们先将“线性相关”与“线性无关”的概念由“有限”向“无限”推广。 对比其它高等代数教程,…...

Spring Security + Jwt 集成实现登录
文章目录 前言Maven 相关依赖配置文件自定义springsecurity相关认证流程继承WebSecurityConfigurerAdapter继承AbstractAuthenticationToken继承AbstractAuthenticationProcessingFilter实现AuthenticationProvider实现UserDetailsService实现AccessDeniedHandler实现Authentic…...
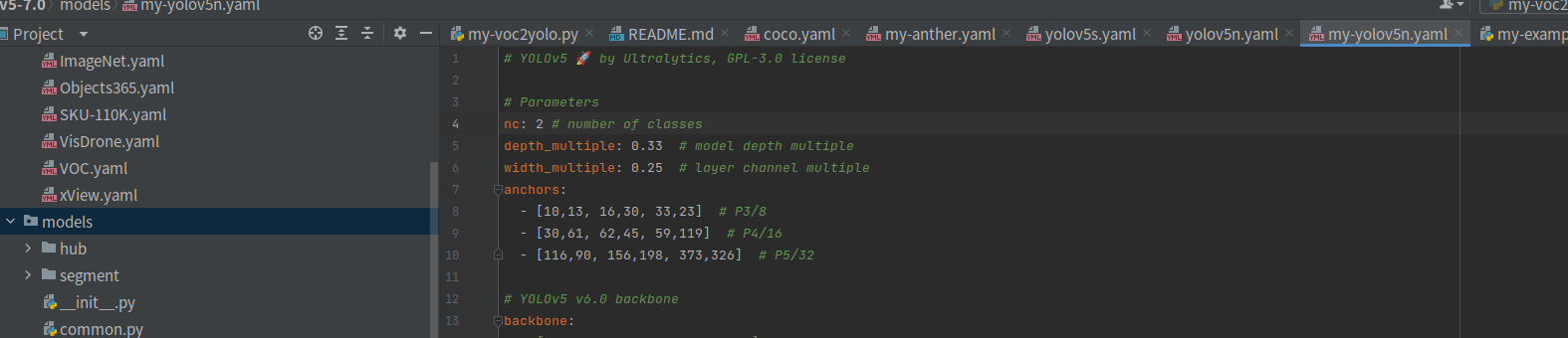
yolov5 用自己的数据集进行训练
在训练之前先要按照一定目录格式准备数据: VOC标签格式转yolo格式并划分训练集和测试集_爱钓鱼的歪猴的博客-CSDN博客 目录 1、修改数据配置文件 2、修改模型配置文件 3、训练 1、修改数据配置文件 coco.yaml 拷贝data/scripts/coco.yaml文件, pa…...
1951-2023最新中国基础地理信息,包括水系、行政区、DEM高程、气象站经纬位置、土地利用,这些数据获取方法介绍
水系: 流域内所有河流、湖泊等各种水体组成的水网系统,称作水系。其中,水流最终流入海洋的称作外流水系,如太平洋水系、北冰洋水系;水流最终流入内陆湖泊或消失于荒漠之中的,称作内流水系。 [1] 流域面积的…...

CAD处理控件Aspose.CAD功能演示:在 C#中以编程方式搜索 DWG 图形文件中的文本
Aspose.CAD 是一个独立的类库,以加强 Java应用程序处理和渲染CAD图纸,而不需要AutoCAD或任何其他渲染工作流程。该CAD类库允许将DWG, DWT, DWF, DWFX, IFC, PLT, DGN, OB…...

实验二十、压控电压源二阶 LPF 幅频特性的研究
一、题目 研究压控电压源二阶低通滤波电路品质因数 Q Q Q 对频率特性的影响。 二、仿真电路 电路如图1所示。集成运放采用 LM324AJ,其电源电压为 15V。 图 1 压控电压源二阶低通滤波电路幅频特性的测试 图1\,\,压控电压源二阶低通滤波电路幅频特性的测试 图1压控…...
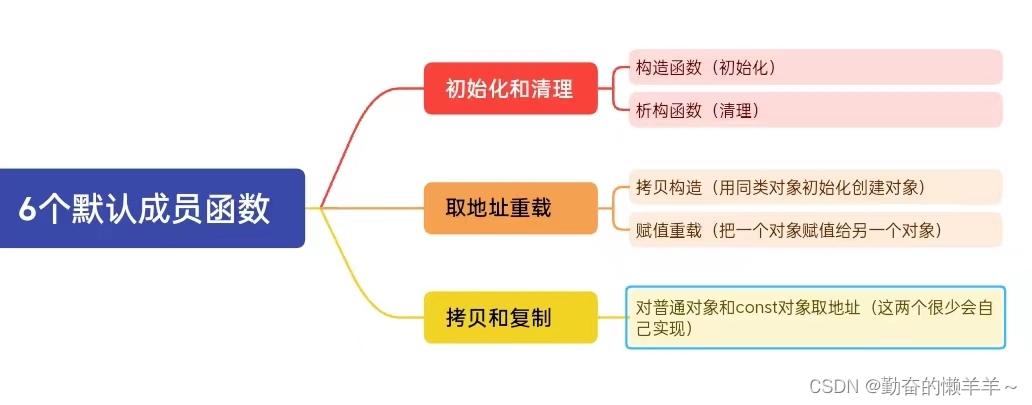
类和对象【C++】【中篇】
目录 一、类的6个默认成员函数 1、构造函数 2、析构函数 3、拷贝构造函数 4、赋值重载函数 二、赋值运算符重载 一、类的6个默认成员函数 注意:默认成员函数不能在类外面定义成全局函数。因为类里没有的话会自动生成,就会产生冲突。 1、构造函数…...

2.SpringBoot运维实用篇
SpringBoot运维实用篇 基础篇发布以后,看到了很多小伙伴在网上的留言,也帮助超过100位小伙伴解决了一些遇到的问题,并且已经发现了部分问题具有典型性,预计将有些问题在后面篇章的合适位置添加到本套课程中,作为解…...

【c++】浅讲引用
【c】浅讲引用 前言引用定义作用做输出型参数引用作返回值总结 关于引用的权限 结尾 前言 博主开始细学c和linux了 这次就带来浅学了的引用。 引用 定义 引用不是在内存中开辟一个新空间的新变量 类似于给变量取别名,和取别名的对象在空间中公用一个对象 例&#…...
)
CSS布局基础(文字[行内<块>]与行内[块]垂直对齐方式 文字溢出显示省略号)
文字[行内<块>]与行内[块]垂直对齐方式 文字[行内<块>]与行内[块]垂直对齐方式概述图片底部空隙问题 文字溢出显示省略号单行文字多行文字 文字[行内<块>]与行内[块]垂直对齐方式 概述 vertical-align: top | middle| bottom | baseline(默认) | sub | sup…...
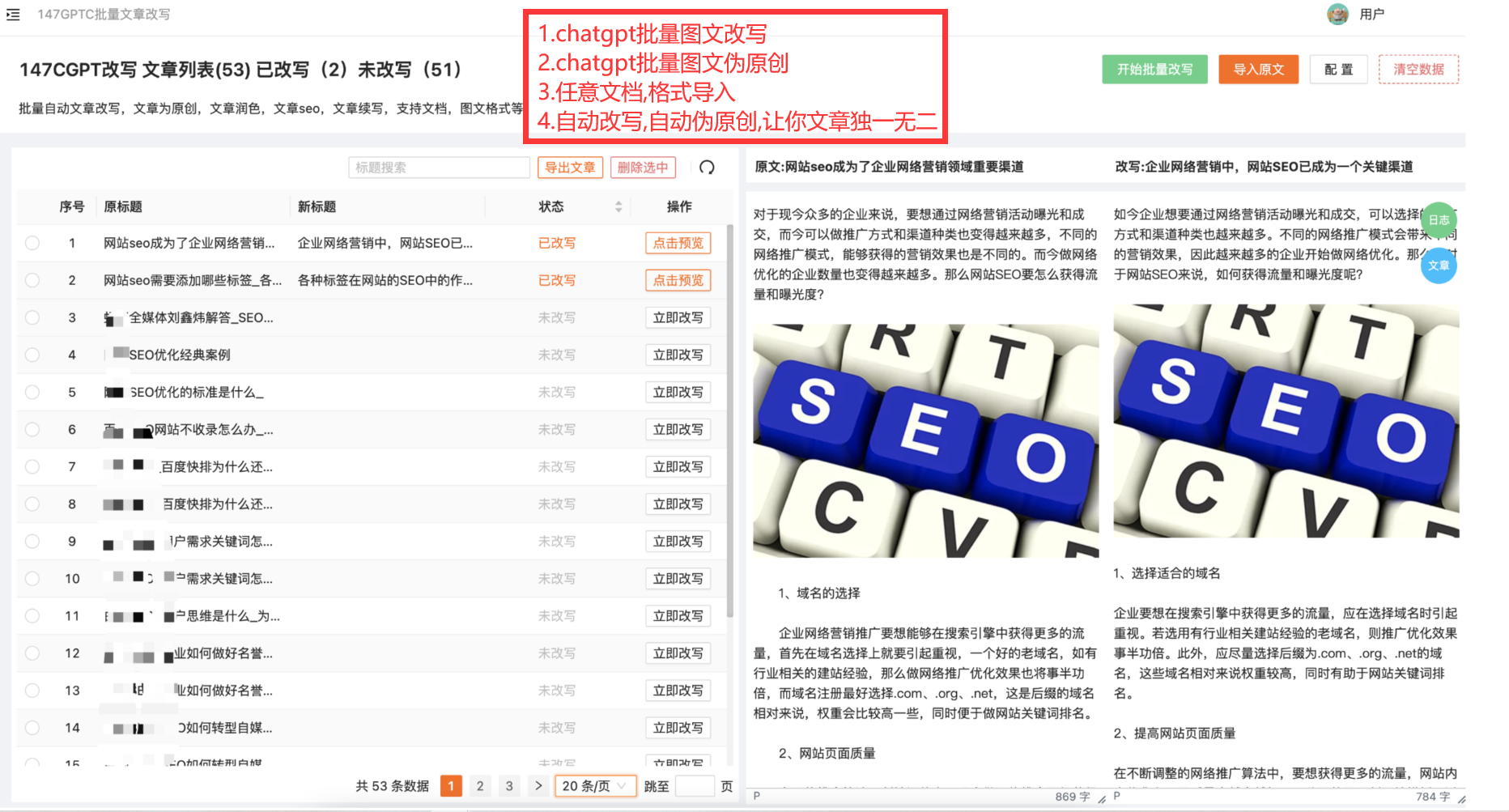
AI自动写文章_免费在线原创文章生成器
自动写文章生成器 自动写文章生成器是一种利用人工智能和自然语言处理技术,帮助用户快速生成文章的工具。该软件可以根据用户的需求和选择,自动生成符合要求的文章,无需手动编写和修改。 自动写文章生成器的主要功能包括以下几个方面&#…...

Java阶段二Day15
Java阶段二Day15 文章目录 Java阶段二Day15复习前日知识点对象数据类型注入数组类型注入集合类型的注入p命名空间引入外部属性文件 基于XML管理beanbean的作用域bean的生命周期代码演示生命周期后置处理器处理展示基于XML的自动装配 基于注解管理bean开启组件扫描使用注解定义B…...
从月薪3000到月薪20000,自动化测试应该这样学...
绝大多数测试工程师都是从功能测试做起的,工作忙忙碌碌,每天在各种业务需求学习和点点中度过,过了好多年发现自己还只是一个功能测试工程师。 随着移动互联网的发展,从业人员能力的整体进步,软件测试需要具备的能力要…...

Python魔法方法 单例模式
前言 本文介绍一下python中常用的魔法方法以及面向对象中非常重要的单例模式。 魔法方法 python中一切皆对象,因为python是面向对象的编程语言。python给类和对象提供了大量的内置方法,这些内置方法也称魔法方法。这些魔法方法总是在某种条件下自动触…...

计算机网络基础知识(三)—— 什么是OSI七层模型?
文章目录 00 | 🛸发展史🛸01 | 🛸OSI七层参考模型🛸02 | 🛸OSI七层参考模型的信息流向🛸 OSI七层模型是Open Systems Interconnection Reference Model的缩写,是由国际标准化组织(IS…...
谐振子牛顿运动方程)
Python(符号计算常微分方程)谐振子牛顿运动方程
牛顿运动方程 牛顿运动方程可以写成以下形式 F d p d t m d v d t m d 2 r d t 2 \mathbf{F}\frac{d \mathbf{p}}{d t}m \frac{d \mathbf{v}}{d t}m \frac{d^2 \mathbf{r}}{d t^2} Fdtdpmdtdvmdt2d2r 恒力问题 具有恒定力的问题意味着恒定的加速度。 典型的例子是…...
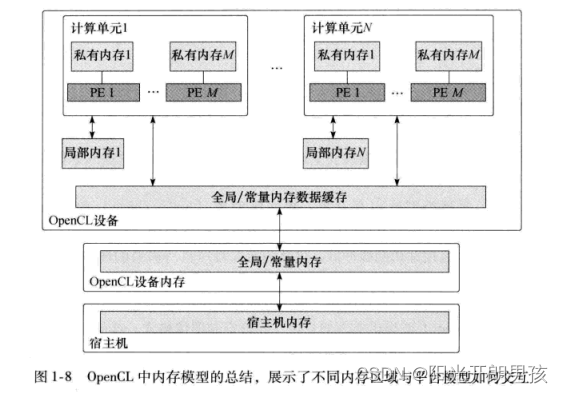
OpenCL编程指南-1.2OpenCL基本概念
OpenCL概念基础 面向异构平台的应用都必须完成以下步骤: 1)发现构成异构系统的组件。 2)探查这些组件的特征,使软件能够适应不同硬件单元的特定特性。 3)创建将在平台上运行的指令块(内核)。 4)…...

使用 ChatGPT 辅助学习——为自己找一个老师
我们每个人都有许多标签,例如高中生、成绩中等、文科,根据这些标签我和其他拥有相同标签的人分配了相同的教程、班级和老师,这可以带来效率上的提升,因为同一份教程、老师就可以服务几十上百人,而无须为每个人定制&…...
用户与权限管理)
MySQL基础(二十一)用户与权限管理
1. 用户管理 1.1 登录MySQL服务器 启动MySQL服务后,可以通过mysql命令来登录MySQL服务器,命令如下: mysql –h hostname|hostIP –P port –u username –p DatabaseName –e "SQL语句"-h参数后面接主机名或者主机IP,…...

程序员的下一个风口
面对近一年的裁员潮,以及 GPT 出现带来的 AI 颠覆潮流,各种话题出现:「前端已死」、「后端已死」、「Copy/Paste 程序员将被 AI 取代」。程序员行业是否还有发展空间? 这一两年的就业机会是因为经济衰落周期内造成的,不…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
