回溯法--N皇后问题
N皇后问题
- 一、问题描述
- 二、示例
- 2.1 四皇后的2个可行解
- 2.2 过程图示
- 三、问题分析
- 3.1涉及到的概念
- 递归
- 回溯
- 3.2 分析
- 四、 代码实现
- 4.1 实现思路
- 宏观:
- 微观:
- 4.2 递归函数NS图
- 4.3 代码
一、问题描述
1、按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
2、n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
二、示例
2.1 四皇后的2个可行解
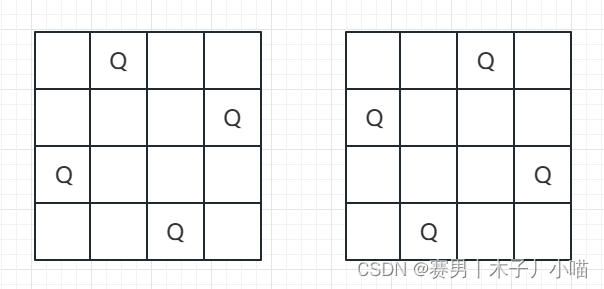
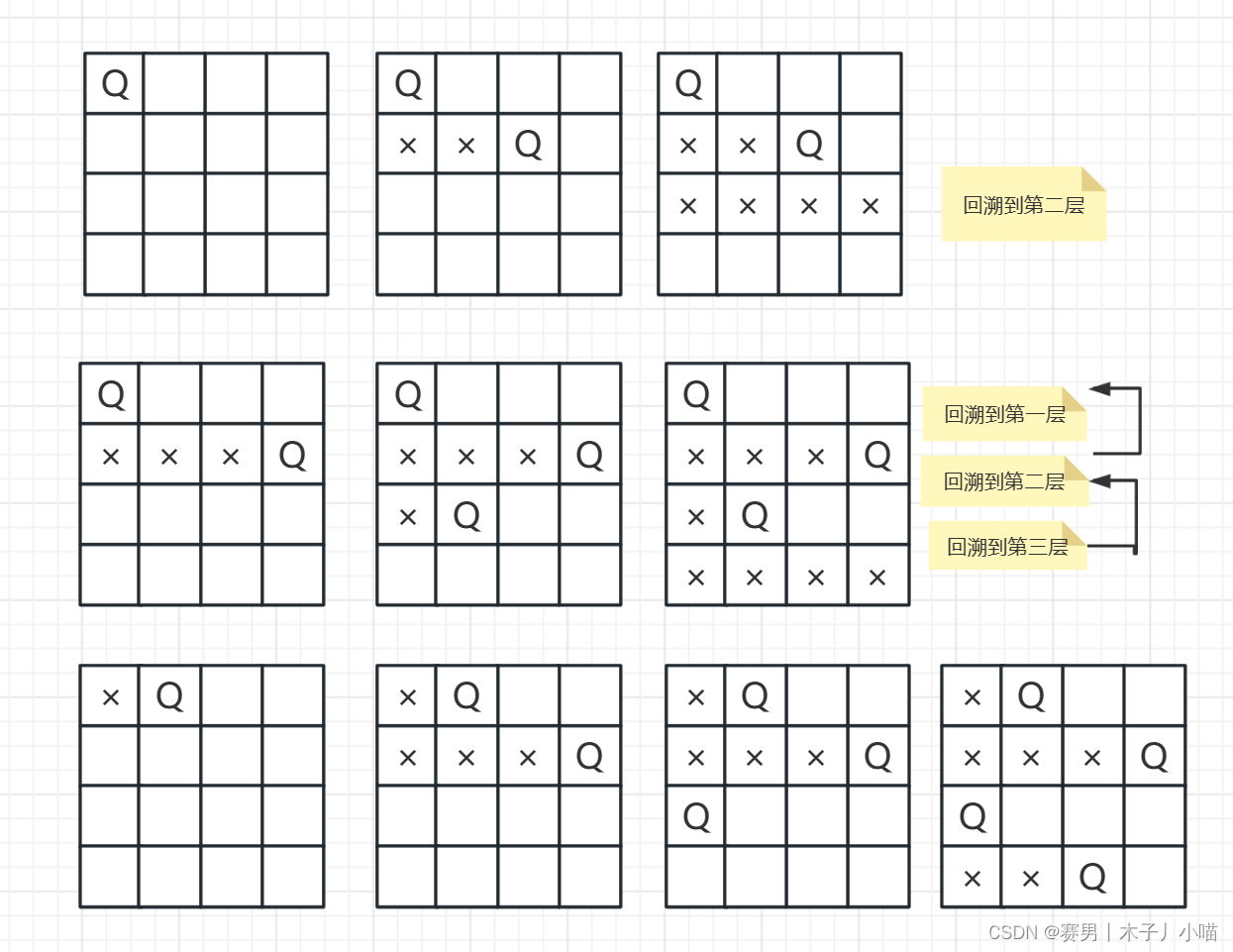
2.2 过程图示
以四皇后为例,展示寻找一种可行解的过程
三、问题分析
3.1涉及到的概念
递归
自己调自己,在方法中调用方法本身。
使用递归需要注意:
1、递归要有出口,不能是死循环,死循环会造成栈溢出。
2、递归次数不宜过多,过多也会有栈溢出的问题。
回溯
回溯法是一种解决问题的算法,它会尝试每一种可能的解决方案来找到最佳解。
3.2 分析
回溯法一般通过递归实现。在n皇后问题中,我们可以从第一行开始,每行放置皇后,检查该皇后是否与之前的皇后冲突,如果没有则放置下一行的皇后,如果发现无解则回溯到上一行重新尝试。
回溯用递归的方式去控制for嵌套的层数,4×4递归4层,每一层有一个for循环,遍历每一层对应的位置。时间复杂度和嵌套for循环一致。
四、 代码实现
4.1 实现思路
宏观:
使用深度搜索的方法,按照先行后列的顺序,查看每一个位置是否满足条件。
微观:
- 定义二维数组表示棋盘,定义一个变量n表示几个皇后
- 定义一个方法用来判断当前摆放的皇后是否与之前的皇后冲突(同列、左上方,右上方),冲突返回0;否则,返回1,表示此位置可以放置皇后。
- 定义一个递归函数,尝试在当前行放置皇后。
这里给一个回溯代码模板
if(终止条件){收集结果;return;
}for(遍历本层集合中的元素){处理节点;递归;回溯,撤销处理结果
}
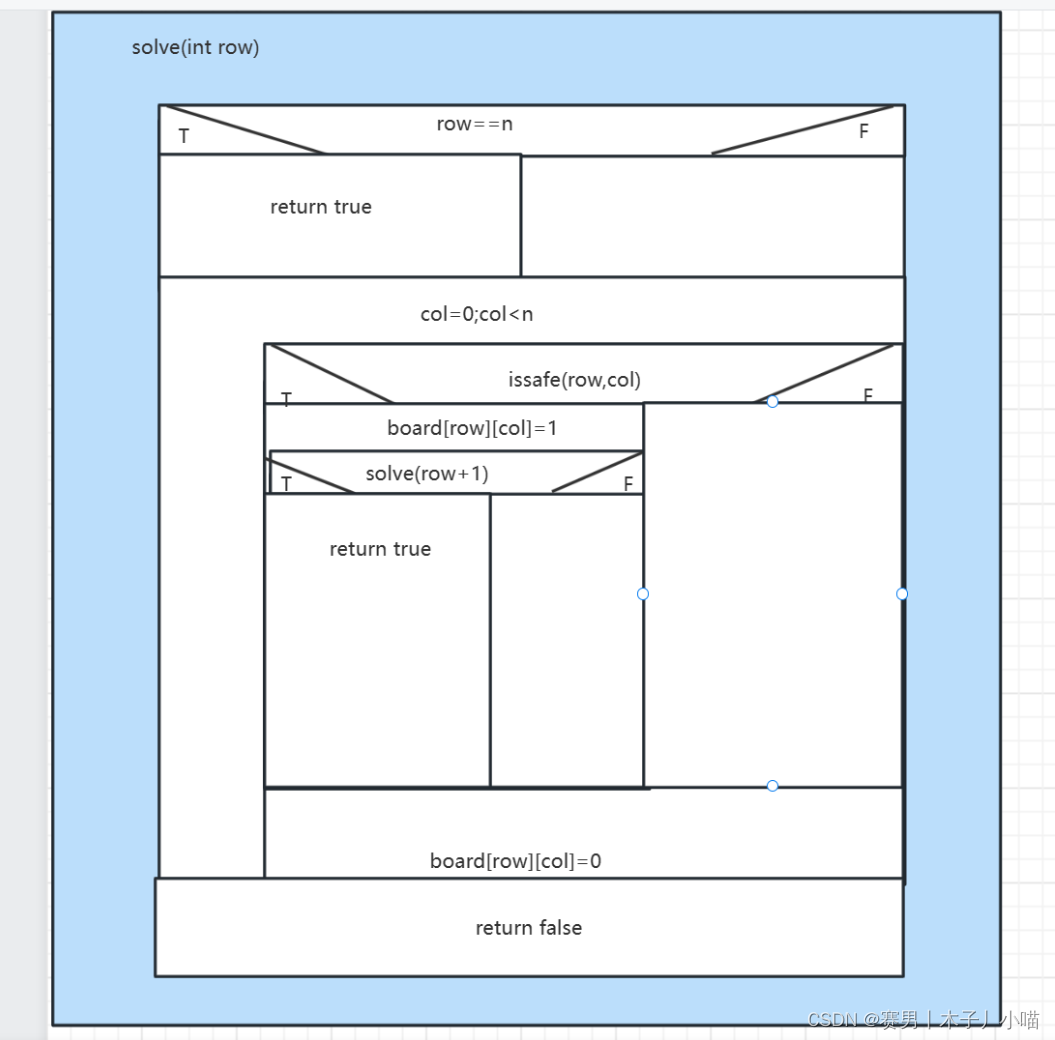
4.2 递归函数NS图
4.3 代码
package com.lsn.NQueen;public class NQueens {// 定义一个二维数组表示棋盘int[][] board;// 定义一个变量表示几个皇后int n;// 构造函数,初始化棋盘和npublic NQueens(int n) {board = new int[n][n];this.n = n;}// 判断当前摆放的皇后是否与之前的皇后冲突public boolean isSafe(int row, int col) {int i, j;// 检查当前列是否有皇后for (i = 0; i < row; i++) {if (board[i][col] == 1) {return false;}}// 检查左上方是否有皇后for (i = row, j = col; i >= 0 && j >= 0; i--, j--) {if (board[i][j] == 1) {return false;}}// 检查右上方是否有皇后for (i = row, j = col; i >= 0 && j < n; i--, j++) {if (board[i][j] == 1) {return false;}}// 如果都没有冲突,则返回truereturn true;}// 递归函数,尝试在当前行放置皇后public boolean solve(int row) {// 如果所有行都已经摆放完毕,则返回true(终止条件,收集结果)if (row == n) {return true;}// 尝试在当前行的每一列放置皇后(单层逻辑,处理节点)for (int col = 0; col < n; col++) {// 判断当前位置是否安全if (isSafe(row, col)) {// 如果安全,则将皇后放置在当前位置board[row][col] = 1;// 递归调用solve函数,尝试在下一行放置皇后if (solve(row + 1)) {return true;}// 如果下一行无法放置皇后,则回溯到当前行,重新尝试放置皇后(撤销处理节点的情况)board[row][col] = 0;}}// 如果当前行的每一列都无法放置皇后,则返回falsereturn false;}// 打印棋盘public void printBoard() {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.print(board[i][j] + " ");}System.out.println();}}public static void main(String[] args) {// 创建一个NQueens对象,并初始化规模为8NQueens nQueens = new NQueens(3);// 调用solve函数,尝试解决N皇后问题if (nQueens.solve(0)) {// 如果找到了解,则打印棋盘nQueens.printBoard();} else {// 如果没有找到解,则打印无解System.out.println("No solution found.");}}
}
相关文章:

回溯法--N皇后问题
N皇后问题 一、问题描述二、示例2.1 四皇后的2个可行解2.2 过程图示 三、问题分析3.1涉及到的概念递归回溯 3.2 分析 四、 代码实现4.1 实现思路宏观:微观: 4.2 递归函数NS图4.3 代码 一、问题描述 1、按照国际象棋的规则,皇后可以攻击与之处…...

ajax请求
ajax的优点 可以无需刷新页面而与服务器进行通信允许你根据用户事件来更新部分页面内容 ajax的缺点 没有浏览历史,不能回退存在跨域问题SEO不友好 get请求 <button>点击发送请求</button><div id"result"></div><script>…...
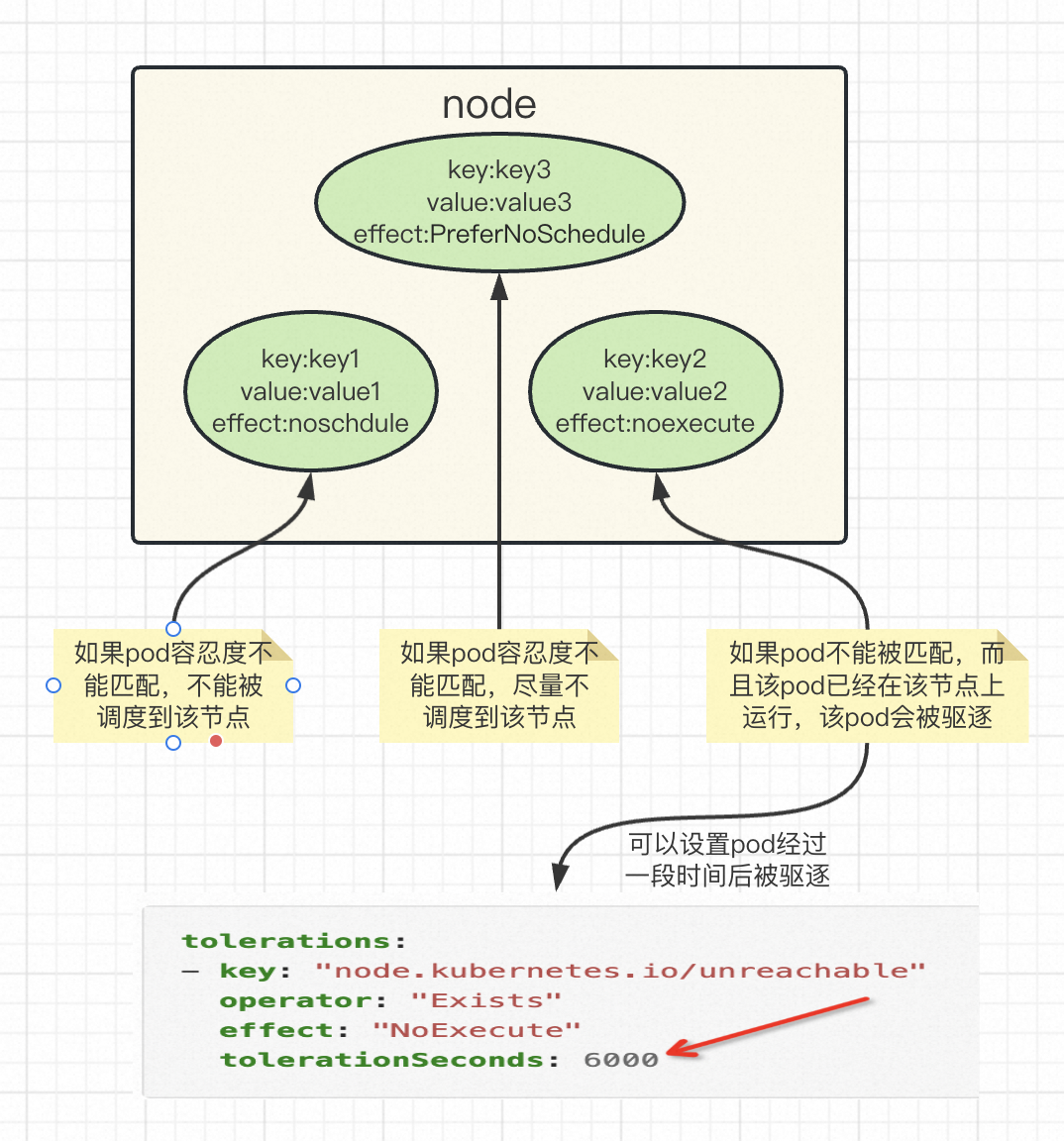
K8S系列之污点和容忍度详细分析
架构图 本篇文档主要介绍污点和容忍度的关系。 污点和容忍度 污点顾名思义就是脏的东西,给节点添加污点来限制pod调度到该节点上,如果pod可以容忍这种污点就可以被调度到有污点的节点上,如果不能容忍就不能被调度到该节点上。 污点作用于节…...

【算法】Minimum Moves to Move a Box to Their Target Location 推箱子
文章目录 Minimum Moves to Move a Box to Their Target Location 推箱子问题描述:分析代码 Tag Minimum Moves to Move a Box to Their Target Location 推箱子 问题描述: 问题 「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓…...
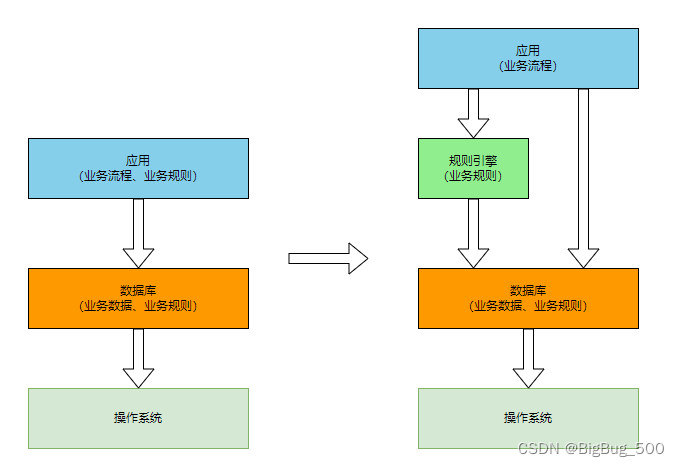
决策引擎平台建设方案
文档修订历史 时间版本主要内容2023.05.12v1.0.0初始化 1. 概述 1.1 需求 1.1.1 需求背景 当同一个业务场景中,有非常多的业务分支后,需要有非常多的 if 判断,来承载这些简单的业务逻辑,但随着业务的发展,业务逐渐…...
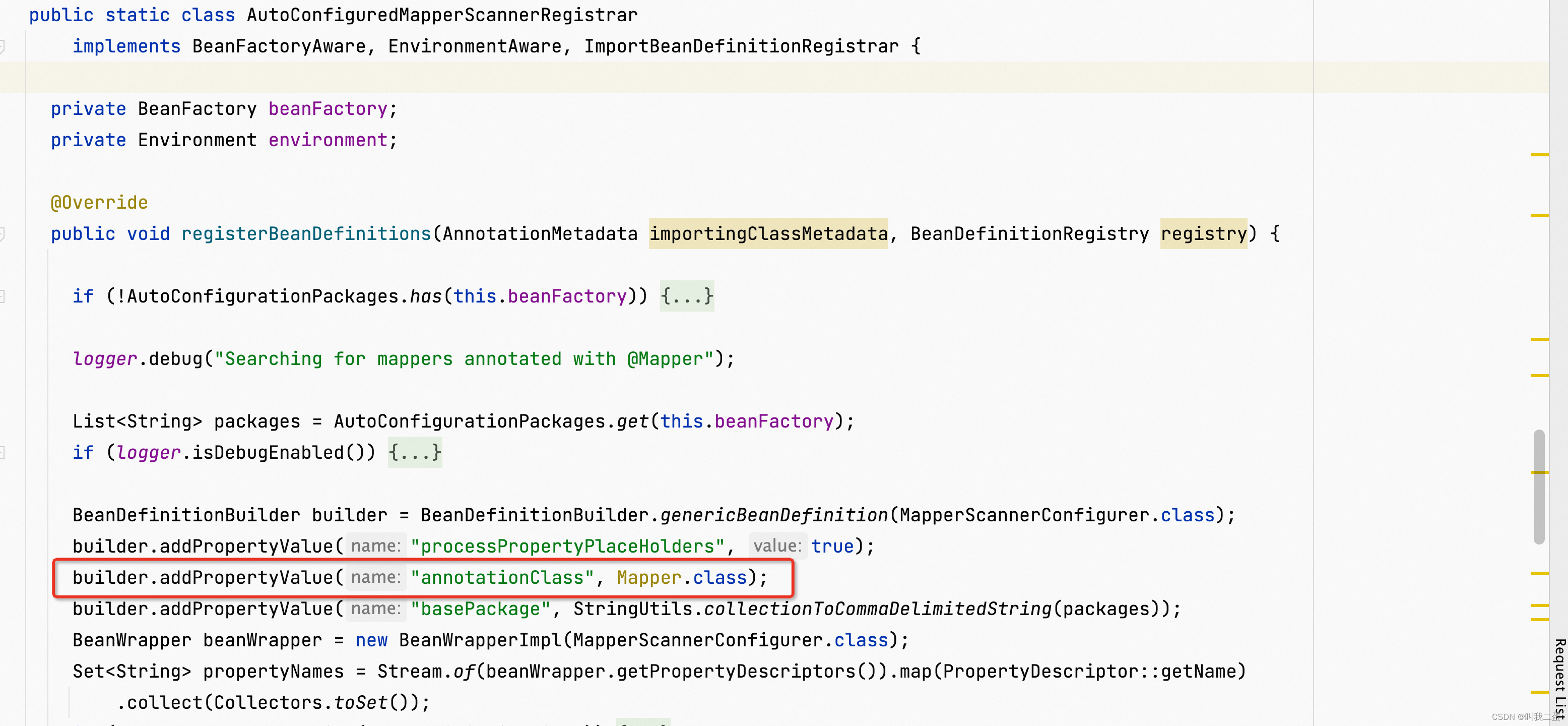
SpringBoot Starter 作用及原理
本文会以 mybatis 为例,通过对比 mybatis-spring 和 mybatis-spring-boot-starter 代码示例,了解 Starter 的作用。并对 mybatis-spring-boot-starter 进行简单剖析,了解 Starter 原理。 下面还有投票,一起参与进来吧👍…...

【rust】| 05——语法基础 | 流程控制
系列文章目录 【rust】| 00——开发环境搭建 【rust】| 01——编译并运行第一个rust程序 【rust】| 02——语法基础 | 变量(不可变?)和常量 【rust】| 03——语法基础 | 数据类型 【rust】| 04——语法基础 | 函数 【rust】| 05——语法基础 | 流程控制 文章目录 流程控制1. 条…...

解决Makefile: recipe for target ‘xxx‘ failed
author daisy.skye的博客_CSDN博客-嵌入式,Qt,Linux领域博主 问题 在android编译Kernel调用makefile引起的recipe for target 很多文章写的是由于编译文件路径引起或者是makefile代码中的空格引起的 分析 但是如果makefile文件不是手动配置的而且源代码提供的,…...

小黑子—多媒体技术与运用基础知识三:数字图形图像处理技术
多媒体技术与运用3.0 多媒体系列第三章1. 颜色科学1.1 颜色的性质1.1.1 颜色的物理性质1.1.2颜色三特性1.1.3三原色与三补色 1.2 颜色空间1.2.1 与设备无关的颜色空间1.2.1 与设备相关的颜色空间 1.3 常见的多媒体系统颜色空间1.3.1 RGB颜色空间1.3.2 CMYK颜色模型1.3.3 HSB颜色…...

Nginx实现ChatGPT API代理
文章目录 一、前言说明二、前置准备三、nginx配置三、代理域名用途 一、前言说明 本篇文章可以直接用于公司生产级的使用,所需要的资源直接改为公司级的即可平替使用文章均已通过实践应用,保证文章准确性,但因不同环境的不同可能效果不一致可…...

FileNotFoundError: [Errno 2] No such file or directory: ‘dot‘
FileNotFoundError: [Errno 2] No such file or directory: ‘dot’ 在绘制树形结构图的时候出现上述报错:已安装环境为ubuntu,python3.9 解决方案: 1、在终端输入sudo apt-get install graphviz,按回车键,输入密码&a…...

【分布族谱】正态分布和二项分布的关系
文章目录 正态分布二项分布验证 正态分布 正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性&am…...

7.设计模式之责任链模式
前言 责任链,即将能够处理同一类请求的对象连成一条链,所提交的请求沿着链传递, 链上的对象逐个判断是否有能力处理该请求,如果能则处理,如果不能则传递给链上的下一个对象。为了避免请求发送者与多个请求处理者耦合在…...

JAVA8的新特性——Stream
JAVA8的新特性——Stream 在这个深夜写下这篇笔记,窗外很安静,耳机里是《季节更替》,我感触还不是很多,当我选择封面图片的时候才发现我们已经渐渐远去,我们都已经奔赴生活,都在拼命想着去换一个活法&#…...

alias设置快捷键vim使用说明(解决服务器上输入长指令太麻烦的问题)
1. vi ~/.bashrc打开 2. (watch -n 1 gpustat 查看gpu使用情况 太麻烦)输入i进行编辑,最后一行输入 alias watchgpuwatch -n 1 gpustat alias gpuwatch -n 1 gpustat alias torch180source activate torch180 3. 按esc,然后输入:wq保存退出 4. source…...

英语基础句型之旅:从基础到高级
英语句型之旅:从基础到高级 一、起步:掌握英语基础句型 (Getting Started: Mastering Basic English Sentence Structures)1.1 英语句子的基本构成 (The Basic Components of English Sentences)1.2 五大基本句型解析 (Analysis of the Five Basic Sente…...
十四、Zuul网关
目录 一、API网关作用: 二、网关主要功能: 2.1、统一服务入口 2.2、接口鉴权 2.3、智能路由 2.4、API接口进行统一管理 2.5、限流保护 三、 新建一个项目作为网关服务器 3.1、项目中引入Zuul网关依赖 3.2、在项目application.yml中配置网关路由…...
5项目五:W1R3S-1(思路为主!)
特别注明:本文章只用于学习交流,不可用来从事违法犯罪活动,如使用者用来从事违法犯罪行为,一切与作者无关。 目录 前言 一、信息收集 二、网页信息的收集 三、提权 总结 前言 思路清晰: 1.信息收集,…...
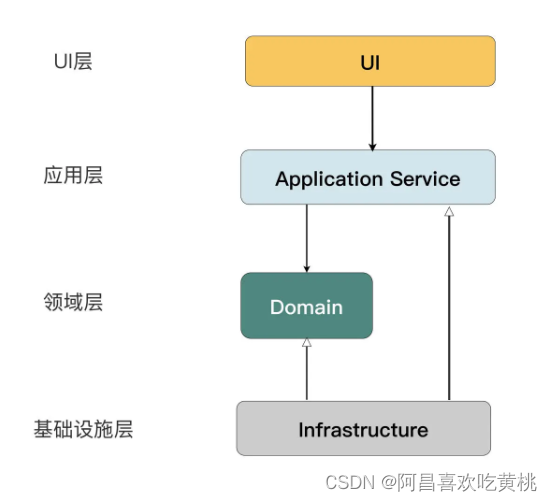
Day958.代码的分层重构 -遗留系统现代化实战
代码的分层重构 Hi,我是阿昌,今天学习记录的是关于代码的分层重构的内容。 来看看如何重构整体的代码,也就是如何对代码分层。 一、遗留系统中常见的模式 一个学校图书馆的借书系统。当时的做法十分“朴素”,在点击“借阅”按钮…...
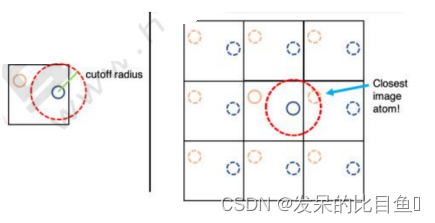
分子模拟力场
分子模拟力场 AMBER力场是在生物大分子的模拟计算领域有着广泛应用的一个分子力场。开发这个力场的是Peter Kollman课题组,最初AMBER力场是专门为了计算蛋白质和核酸体系而开发的,计算其力场参数的数据均来自实验值,后来随着AMBER力场的广泛…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
