【分布族谱】正态分布和二项分布的关系
文章目录
- 正态分布
- 二项分布
- 验证
正态分布
正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性,使得正态分布拥有广泛的应用场景,或许正因如此,正太分布在分布族谱图中居于核心的位置。
正态分布 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)受到期望 μ \mu μ和方差 σ 2 \sigma^2 σ2的调控,其概率密度函数为
1 2 π σ 2 exp [ − ( x − μ ) 2 2 σ 2 ] \frac{1}{\sqrt{2\pi\sigma^2}}\exp[-\frac{(x-\mu)^2}{2\sigma^2}] 2πσ21exp[−2σ2(x−μ)2]
当 μ = 0 \mu=0 μ=0而 σ = 1 \sigma=1 σ=1时,为标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),对应概率分布函数为 Φ ( x ) = 1 2 π exp [ − x 2 2 ] \Phi(x)=\frac{1}{\sqrt{2\pi}}\exp[-\frac{x^2}{2}] Φ(x)=2π1exp[−2x2],形状如下,

在scipy.stats中,分别封装了正态分布类norm和标准正态分布类halfnorm。
二项分布
二项分布是非常简单而又基础的一种离散分布,貌似是高中学到的第一个分布,就算不是第一个,也是第一批。在 N N N次独立重复的伯努利试验中,设A在每次实验中发生的概率均为 p p p。则 N N N次试验后A发生 k k k次的概率分布,就是二项分布,记作 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p),则
P { X = k } = ( n k ) p k ( 1 − p ) n − k P\{X=k\}=\binom{n}{k}p^k(1-p)^{n-k} P{X=k}=(kn)pk(1−p)n−k
其中 ( n k ) = n ! k ! ( n − k ) ! \binom{n}{k}=\frac{n!}{k!(n-k)!} (kn)=k!(n−k)!n!,高中的写法一般是 C n k C^k_n Cnk。
记 q = 1 − p q=1-p q=1−p,令 x k = k − n p n p q x_k=\frac{k-np}{\sqrt{npq}} xk=npqk−np,当 n n n趋近于无穷大时,根据De Moivre–Laplace定理,有
lim n → ∞ n ! k ! ( n − k ) ! p k q n − k ≈ 1 2 π n p q e ( k − n p ) 2 2 n p q \lim_{n\to\infty}\frac{n!}{k!(n-k)!}p^kq^{n-k}\approx\frac{1}{\sqrt{2\pi npq}}e^{\frac{(k-np)^2}{2npq}} n→∞limk!(n−k)!n!pkqn−k≈2πnpq1e2npq(k−np)2
即服从 σ 2 = n p q , μ = n p \sigma^2=npq, \mu=np σ2=npq,μ=np的高斯分布。
验证
下面通过scipy.stats对二项分布和高斯分布之间的关联进行验证
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ssp,q = 0.2, 0.8
ns = [10, 100, 1000, 10000]fig = plt.figure()
for i,n in enumerate(ns):rs = ss.binom(n, p).rvs(50000)rv = ss.norm(n*p, np.sqrt(n*p*q))st, ed = rv.interval(0.999)xs = np.linspace(st, ed, 100)ys = rv.pdf(xs)ax = fig.add_subplot(2,2,i+1)ax.hist(rs, density=True, bins='auto', alpha=0.2)ax.plot(xs, ys)plt.title(f"n={n}")plt.show()
效果如下,可见随着 n n n越来越大,二项分布的随机数越来越靠近正态分布的概率密度曲线

相关文章:

【分布族谱】正态分布和二项分布的关系
文章目录 正态分布二项分布验证 正态分布 正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性&am…...

7.设计模式之责任链模式
前言 责任链,即将能够处理同一类请求的对象连成一条链,所提交的请求沿着链传递, 链上的对象逐个判断是否有能力处理该请求,如果能则处理,如果不能则传递给链上的下一个对象。为了避免请求发送者与多个请求处理者耦合在…...

JAVA8的新特性——Stream
JAVA8的新特性——Stream 在这个深夜写下这篇笔记,窗外很安静,耳机里是《季节更替》,我感触还不是很多,当我选择封面图片的时候才发现我们已经渐渐远去,我们都已经奔赴生活,都在拼命想着去换一个活法&#…...

alias设置快捷键vim使用说明(解决服务器上输入长指令太麻烦的问题)
1. vi ~/.bashrc打开 2. (watch -n 1 gpustat 查看gpu使用情况 太麻烦)输入i进行编辑,最后一行输入 alias watchgpuwatch -n 1 gpustat alias gpuwatch -n 1 gpustat alias torch180source activate torch180 3. 按esc,然后输入:wq保存退出 4. source…...

英语基础句型之旅:从基础到高级
英语句型之旅:从基础到高级 一、起步:掌握英语基础句型 (Getting Started: Mastering Basic English Sentence Structures)1.1 英语句子的基本构成 (The Basic Components of English Sentences)1.2 五大基本句型解析 (Analysis of the Five Basic Sente…...
十四、Zuul网关
目录 一、API网关作用: 二、网关主要功能: 2.1、统一服务入口 2.2、接口鉴权 2.3、智能路由 2.4、API接口进行统一管理 2.5、限流保护 三、 新建一个项目作为网关服务器 3.1、项目中引入Zuul网关依赖 3.2、在项目application.yml中配置网关路由…...
5项目五:W1R3S-1(思路为主!)
特别注明:本文章只用于学习交流,不可用来从事违法犯罪活动,如使用者用来从事违法犯罪行为,一切与作者无关。 目录 前言 一、信息收集 二、网页信息的收集 三、提权 总结 前言 思路清晰: 1.信息收集,…...
Day958.代码的分层重构 -遗留系统现代化实战
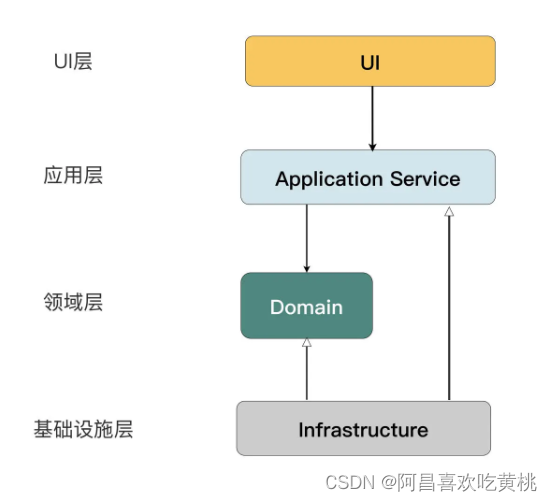
代码的分层重构 Hi,我是阿昌,今天学习记录的是关于代码的分层重构的内容。 来看看如何重构整体的代码,也就是如何对代码分层。 一、遗留系统中常见的模式 一个学校图书馆的借书系统。当时的做法十分“朴素”,在点击“借阅”按钮…...
分子模拟力场
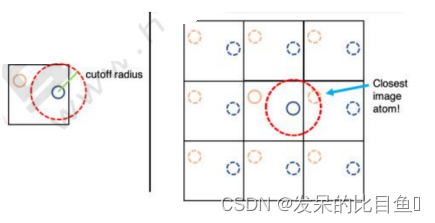
分子模拟力场 AMBER力场是在生物大分子的模拟计算领域有着广泛应用的一个分子力场。开发这个力场的是Peter Kollman课题组,最初AMBER力场是专门为了计算蛋白质和核酸体系而开发的,计算其力场参数的数据均来自实验值,后来随着AMBER力场的广泛…...

ERP 系统在集团化企业财务管理中的应用
(一)集团统一会计核算平台的构建原理及功能 第一,搭建集中统一会计核算平台的基础是确定财务组 织及岗位,在此基础上制定统一的会计核算政策、规范集中 基础数据、落实内控管理制度。 第二,具备了以上建立集中统一会计…...

达摩院开源多模态对话大模型mPLUG-Owl
miniGPT-4的热度至今未减,距离LLaVA的推出也不到半个月,而新的看图聊天模型已经问世了。今天要介绍的模型是一款类似于miniGPT-4和LLaVA的多模态对话生成模型,它的名字叫mPLUG-Owl。 论文链接:https://arxiv.org/abs/2304.14178…...

Group相关问题-组内节点限制移动范围
1.在节点中定义dragComputation,限制节点的移动范围 注意事项 组节点不定义go.Placeholder ,设置了占位符后组内节点移动将改变组节点位置dragComputation中自定义stayInGroup计算规则是根据groupNode的resizeObject计算 如果开启了resizable:true,建议指定其改变大的零部件r…...

程序员该如何学习技术
程序员该如何学习技术 前言 学习是第一生产力,我从来都是这么认为的,人只有只有不断地学习才能意识到自己的缺点和不足,身为程序员,我更认为人们应当抱着终身学习的想法实践下去,这是我所一直践行且相信的。 高处不胜寒…...

springboot+vue交流互动系统(源码+文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的交流互动系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 💕💕作者:风歌&a…...

【2023华为OD笔试必会25题--C语言版】《01 预定酒店》——排序、二分查找
本专栏收录了华为OD 2022 Q4和2023Q1笔试题目,100分类别中的出现频率最高(至少出现100次)的25道,每篇文章包括原始题目 和 我亲自编写并在Visual Studio中运行成功的C语言代码。 仅供参考、启发使用,切不可照搬、照抄,查重倒是可以过,但后面的技术面试还是会暴露的。✨✨…...

C语言实现队列--数据结构
😶🌫️Take your time ! 😶🌫️ 💥个人主页:🔥🔥🔥大魔王🔥🔥🔥 💥代码仓库:🔥🔥魔…...

前端CSS经典面试题总结
前端CSS经典面试题总结 2.1 介绍一 下 CSS 的盒子模型?2.2 css 选择器优先级?2.3 垂直居中几种方式?2.4 简明说一下 CSS link 与 import 的区别和用法?2.5 rgba和opacity的透明效果有什么不同?2.6 display:none和visib…...
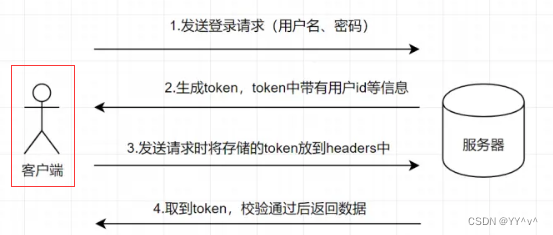
cookie、session、token的区别是什么
前言 今天就来说说session、cookie、token这三者之间的关系!最近这仨玩意搞得头有点大🤣 1.为什么会有它们三个? 我们都知道 HTTP 协议是无状态的,所谓的无状态就是客户端每次想要与服务端通信,都必须重新与服务端链接…...

leetcode分类刷题 -- 前缀和和哈希
力扣 class Solution { public int subarraySum(int[] nums, int k) { Map<Integer,Integer> map new HashMap<>(); int count0,sum0; map.put(0,1); for(int i:nums){ sum i; if(map.containsKey(sum-k)) count map.get(sum-k); map.compute(sum,(key,v)->…...

浅谈作为程序员如何写好文档:了解读者
我作为从一名懵懂的实习生转变为工程师的工作经历中,伴随着技术经验的成长,也逐渐意识到了编写文档是知识和经验传递给其他人的最有效方式。通过文档,可以分享我的技术知识和最佳实践,使其他人更好地理解我的工作。在这里…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
