《程序员面试金典(第6版)》面试题 16.19. 水域大小(深度优先搜索,类似棋盘类问题,八皇后的简化版本,C++)
题目描述
你有一个用于表示一片土地的整数矩阵land,该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。
池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小,返回值需要从小到大排序。
示例:
输入:
[[0,2,1,0],[0,1,0,1],[1,1,0,1],[0,1,0,1]
]
输出: [1,2,4]
提示:
- 0 < len(land) <= 1000
- 0 < len(land[i]) <= 1000
原题链接
解题思路与代码
首先,这道题是一道有意思的思考题,有点类似于棋盘类的题型了。
一上来大家可能有点懵,但是仔细想想或者看过题目下面的相关提示后,可能就会想,哦,这道题我们可以用深度优先搜索去做呀~
其实在做这道题的过程中,我感觉这道题可以算是一道类似棋盘类的问题了,可以说可以算是八皇后的简单版本。因为我们同样要去设置一个标记数组,去记录某一个格子是否已经被记录过了。也要检查多个方向等。
言归正传,让我们来讲解一下这道题到底是如何用深度搜索做的。
- 首先让我们创建一个记录结果的数组,result,一个二维标记数组visit。
- 准备好之后,我们开始用双层for循环,从左到右从上到下的去遍历每一个棋子。
- 只有当这个棋子在land中被记录为0,并且没有被标记数组标记过,我们才能进入这个棋子的递归。
- 这个递归函数会检查一个棋子的8个方向上都有没有池塘,如果有,则标记这个棋子,最后返回一个int值,代表这个池塘有多少块水域。
- 我们会把这个池塘添加到result中去,最后把result排个序,之后返回就可以了。
具体代码如下:
class Solution {
public:vector<int> pondSizes(vector<vector<int>>& land) {vector<int> result;int m = land.size();int n = land[0].size();vector<vector<bool>> visit(m,vector<bool>(n,false));for(int i = 0; i < m; ++i)for(int j = 0; j < n; ++j)if(land[i][j] == 0 && !visit[i][j]){int size = dfs(land,visit,i,j);result.push_back(size);}sort(result.begin(),result.end());return result;}int dfs(vector<vector<int>>& land, vector<vector<bool>>& visit,int i, int j){if(i < 0 || j < 0 || i >= land.size() || j >=land[0].size() || land[i][j] != 0 || visit[i][j])return 0;int size = 1;visit[i][j] = true;for(int r = -1; r <= 1; ++r)for(int c = -1; c <= 1; ++c)size += dfs(land,visit,i + r,j + c);return size;}
};

复杂度分析
时间复杂度:
- 在最坏的情况下,我们需要遍历土地矩阵中的每个单元格,并可能需要进行深度优先搜索。因此,时间复杂度为O(n^2)。
空间复杂度:
- 我们需要一个与土地矩阵大小相同的visited矩阵来跟踪每个单元格是否已被访问。此外,由于我们使用了递归,因此还需要考虑调用堆栈的空间。在最坏的情况下,可能需要进行m*n次递归调用(例如,当所有单元格都是水域时)。因此,空间复杂度也为O(n^2)。
当我们说深度优先搜索的时间复杂度是O(n^2)时,我们是指最坏的情况下,我们需要访问土地矩阵中的每一个单元格。在这个过程中,每个单元格可能会被DFS函数访问多次(最多9次,包括自身和周围的8个邻居),但是每个单元格只会被处理(即被加入到某个池塘的大小中)一次,因为一旦一个单元格被处理,我们就会将其标记为已访问,之后就不会再处理它了。
因此,虽然DFS函数可能会被调用多于n^2 次,但是我们只需要进行n^2 次实际的处理,所以时间复杂度仍然是O(n^2)。
总结
-
这道题目主要是为了考察求解者对深度优先搜索(DFS)和图遍历的理解和应用能力。
-
在实际应用中,这种类型的问题可能出现在一些地理信息系统(GIS)或者环境科学的领域,比如:
-
水体识别和测量:这个问题可以用于识别和测量地图上的水体。给定一张地形图(通过海拔高度表示),我们可以计算出地图上水体(海拔高度为0的区域)的数量和大小。
-
连通区域识别:在计算机视觉或图像处理中,这个问题可以用于识别图像中的连通区域。例如,我们可以使用类似的方法来识别和测量图像中的特定颜色或纹理的区域。
-
地图路径规划:这个问题也可以用于规划地图上的路径。例如,我们可以使用DFS来寻找从一点到另一点的路径,或者寻找所有可以到达的点。
-
通过这道题,你可以加深对深度优先搜索(DFS)算法的理解,这对于很多图论问题和搜索问题的解决都是非常有帮助的。
最后的最后,如果你觉得我的这篇文章写的不错的话,请给我一个赞与收藏,关注我,我会继续给大家带来更多更优质的干货内容。
相关文章:

《程序员面试金典(第6版)》面试题 16.19. 水域大小(深度优先搜索,类似棋盘类问题,八皇后的简化版本,C++)
题目描述 你有一个用于表示一片土地的整数矩阵land,该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小,返回值需要从小到…...
Spring 注解之@RestController与@Controller的区别
目录 1:介绍 2:区别 3:总体来说 4:社区地址 1:介绍 RestController 和 Controller 是 Spring MVC 中常用的两个注解,它们都可以用于定义一个控制器类。 2:区别 返回值类型不同:…...

Java中的泛型是什么?如何使用泛型
Java中的泛型是指在定义类、接口和方法时使用类型参数,以使得这些类、接口和方法可以操作多种类型的数据,从而提高代码的重用性和安全性。Java的泛型机制是从JDK5开始引入的,它使得Java程序员能够编写更加通用和类型安全的代码。 什么是泛型…...

【飞行棋】多人游戏-微信小程序开发流程详解
可曾记得小时候玩过的飞行棋游戏,是90后的都有玩过吧,现在重温一下,这是一个可以二到四个人参与的游戏,通过投骰子走棋,一开始靠运气,后面还靠自己选择,谁抢占先机才能赢,还可以和小…...

力扣 146. LRU 缓存
一、题目描述 请你设计并实现一个满足LRU(最近最少使用)缓存约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以正整数作为容量 capacity 初始化LRU缓存。int get(int key) 如果关键字 key 存在于缓存中,则返回关键…...

关于Oracle SCN的最大阈值
SCN每秒增长的速度跟Oracle的版本有关,在Oracle 11.2.0.2之前是每秒允许最大增长16384,在Oracle 11.2.0.2之后是默认每秒允许增长32768,这个值跟新增的隐含参数_max_reasonable_scn_rate有关,如下所示: NAME …...

Linux多路转接之poll
文章目录 一、poll的认识二、编写poll方案服务器三、poll方案多路转接的总结 一、poll的认识 多路转接技术是在不断更新进步的,一开始多路转接采用的是select方案,但是select方案存在的缺点比较多,所以在此基础上改进,产生了poll…...

Webpack打包流程
轻松了解Webpack 打包流程 Webpack是一个现代的JavaScript应用程序的静态模块打包器。它将多个JavaScript文件打包成一个或多个静态资源文件,以便在浏览器中加载。Webpack将应用程序视为一个依赖项图,其中包括应用程序的所有模块,然后通过该…...

React事件委托
React 事件委托(Event Delegation)是一种优化事件处理的技术,它通过将事件监听器添加到父级元素(而不是子元素)来实现。当事件触发时,事件会向上冒泡到父元素,然后在父元素上调用事件处理函数。…...
Notion——构建个人知识库
前言 使用Notion快三年了,它All in one的理念在使用以后确实深有体会,一直想找一个契机将这个软件分享给大家,这款笔记软件在网上已经有很多的教程了,所以在这里我主要想分享框架方面的内容给大家,特别对于学生党、研究…...

ModuleNotFoundError: No module named ‘Multiscaledeformableattention‘
在实现DINO Detection方法时,我们可能会遇到以上问题。因为在DeformableAttention模块,为了加速,需要自己去编译这个模块。 如果你的环境变量中能够找到cuda路径,使用正确的torch版本和cuda版本的话,这个问题很容易解…...

【数据结构】链表(C语言实现)
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c语言系列专栏:c语言之路重点知识整合 &#x…...
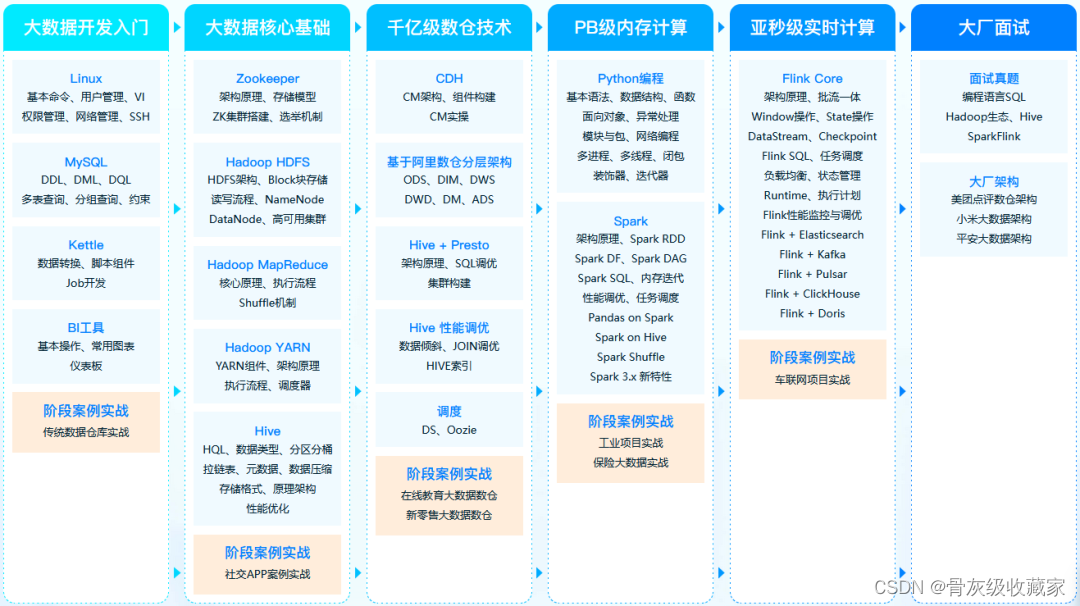
【2023程序员必看】大数据行业分析
1、政策重点扶持,市场前景广阔 2014年,大数据首次写入政府工作报告,大数据逐渐成为各级政府关注的热点。 2015年9月,国务院发布《促进大数据发展的行动纲要》,大数据正式上升至国家战略层面,十九大报告提…...
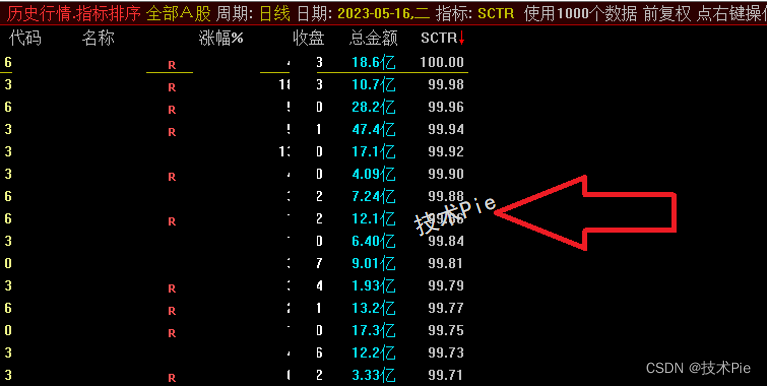
通达信SCTR强势股选股公式,根据六个技术指标打分
SCTR指标(StockCharts Technical Rank)的思路来源于著名技术分析师约翰墨菲,该指标根据长、中、短三个周期的六个关键技术指标对股票进行打分,根据得分对一组股票进行排名,从而可以识别出强势股。 与其他技术指标一样,SCTR的设计…...
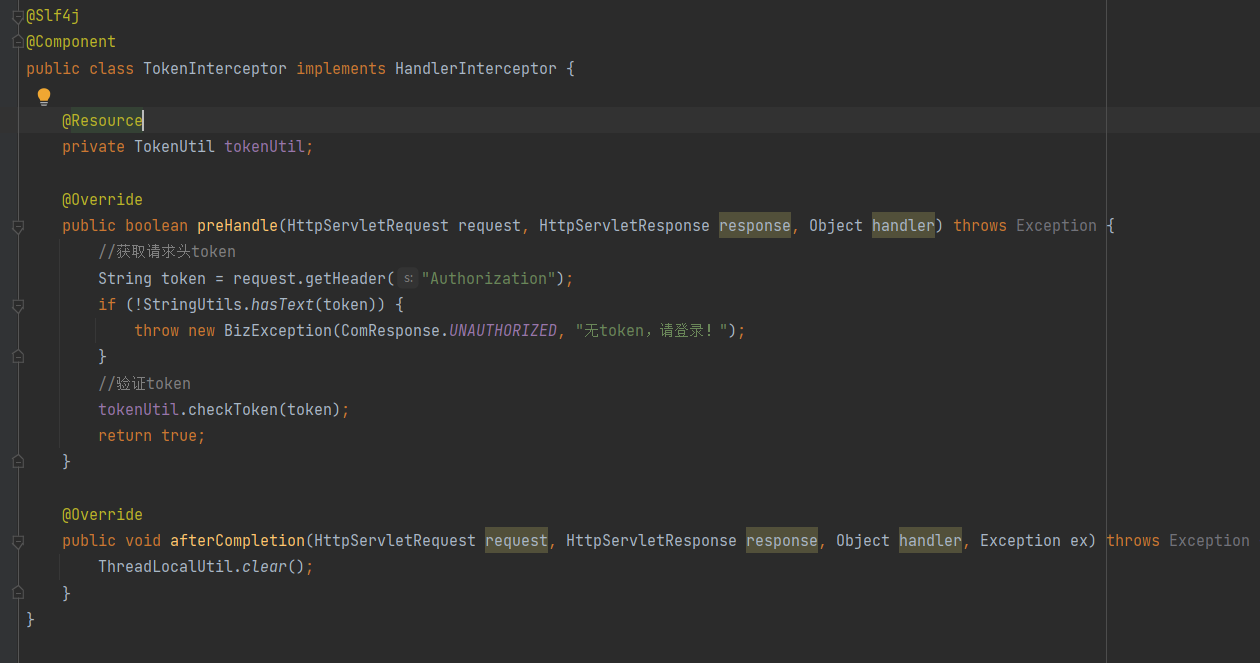
SpringBoot+Token+Redis+Lua+自动续签极简分布式锁Token登录方案
前言 用SpringBoot做一个项目,都要写登录注册之类的方案 使用Cookie或Session的话,它是有状态的,不符合现代的技术 使用Security或者Shiro框架实现起来比较复杂,一般项目无需用那么复杂 使用JWT它虽然是无状态的,也可…...
多模态:MiniGPT-4
多模态:MiniGPT-4 IntroductionMethodlimitation参考 Introduction GPT-4具有很好的多模态能力,但是不开源。大模型最近发展的也十分迅速,大模型的涌现能力可以很好的迁移到各类任务,于是作者猜想这种能力可不可以应用到多模态模…...
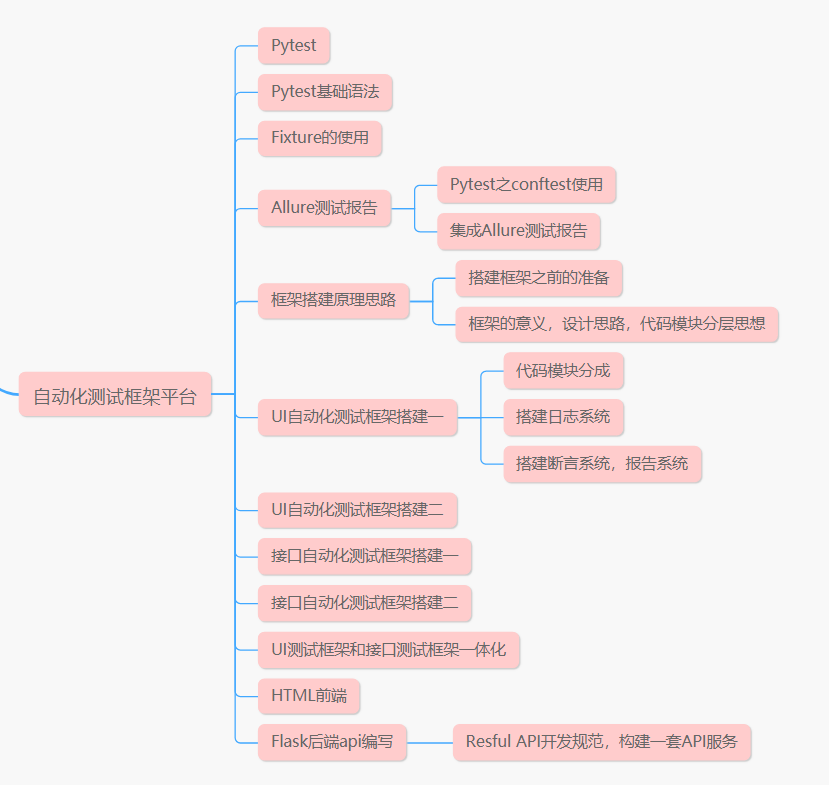
5年时间里,自动化测试于我带来的意义,希望你也能早点知道
摘要:在我有限的软件测试经历里,曾有一段专职的自动化测试经历。 接触自动化 那时第一次上手自动化测试,团队里用的是Python,接口自动化测试的框架是requestsExcelJenkins,APP自动化测试的框架是Appium。 整个公司当…...
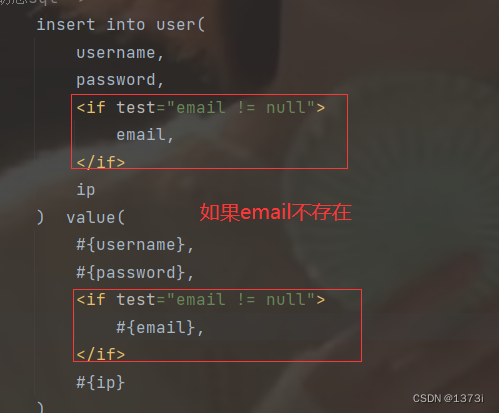
【MyBaits】SpringBoot整合MyBatis之动态SQL
目录 一、背景 二、if标签 三、trim标签 四、where标签 五、set标签 六、foreach标签 一、背景 如果我们要执行的SQL语句中不确定有哪些参数,此时我们如果使用传统的就必须列举所有的可能通过判断分支来解决这种问题,显示这是十分繁琐的。在Spring…...

涅槃重生,BitKeep如何闯出千万用户新起点
在全球,BitKeep钱包现在已经有超过千万用户在使用。 当我得知这个数据的时候,有些惊讶,也有点意料之中。关注BitKeep这几年,真心看得出这家公司的发展之迅速。还记得2018年他们推出第一个版本时,小而美,简洁…...

绝地求生 压枪python版
仅做学习交流,非盈利,侵联删(狗头保命) 一、概述 1.1 效果 总的来说,这种方式是通过图像识别来完成的,不侵入游戏,不读取内存,安全不被检测。 1.2 前置知识 游戏中有各种不同的枪械&#x…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
