MATLAB连续LTI系统的时域分析(十)
目录
1、实验目的:
2、实验内容:
1、实验目的:
1)掌握利用MATLAB对系统进行时域分析的方法;
2)掌握连续时间系统零输入响应的求解方法;
3)掌握连续时间系统零状态响应、冲激响应和阶跃响应的求解方法;
4)掌握利用计算机进行卷积积分和卷积和计算的方法。
2、实验内容:
2-1)、已知某系统可以由如下微分方程描述y′′(t)+ y′(t)+6y(t)=x(t),利用MATLAB绘出该系统冲激响应和阶跃响应的时域波形。(注:题中时域范围可取[0 10],参考函数tf、impulse、step)
a = [1 1 6]; b = [1]; %微分方程左右两端多项式的系数矩阵
time = 0:0.01:10; %时域范围[0 10]
sys = tf(b,a);
y1 = impulse(sys,time); %系统的冲激响应
y2 = step(sys,time); %系统的阶跃响应
subplot(1,2,1), plot(time,y1), xlabel('时间t'), title('冲激响应');
subplot(1,2,2), plot(time,y2), xlabel('时间t'), title('阶跃响应');2-2)、编程实现如下图所示的两个波形的卷积,并绘制出卷积后的波形。(要求:先构建两信号卷积函数,而后通过调用该函数实现做题)
编写的卷积函数
function [t,x] = sss_conv(x1,x2,t1,t2,dt)
%文件名与函数名对应
%自写的卷积函数
x = conv(x1,x2)*dt;
t0 = t1(1) + t2(1);
L = length(x1) + length(x2)-2;
t = t0:dt:(t0+L*dt);
end功能实现
dt = 0.01;
x1 = -1 : dt : 1;
f1t = 2*(heaviside(x1+1) - heaviside(x1-1));
% plot(x1,f1t);
x2 = -2 : dt : 2;
f2t = heaviside(x2+2) - heaviside(x2-2);
% plot(x2,f2t);
[t, f] = My_conv(f1t, f2t, x1, x2, dt); %调用卷积函数
plot(t, f);
axis([-4 4 -1 5]);2-3)、已知系统的微分方程为:,x(t)为e-tu(t),用数值法求零状态响应y(t)并绘图。(注:题中时域范围可取[0 10])
a = [1 4 4]; b = [1 3]; dt = 0.1; t = 0:dt:10; % 微分方程左侧系数向量a,微分方程右侧系数向量b
[r,p] = residue(b,a); % 用residue函数(参见12.1.2节)求出其特征根p1、p2和相应的留数r1、r2h = r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t); %叠加各根分量
subplot(1,2,1), plot(t,h), title('冲激响应');
x = exp(-t); % t已经大于0了
y = conv(x,h)*dt; % 求x和h的卷积,长度为2*length(t)-1
subplot(1,2,2), plot(t,y(1:length(t))), title('零状态响应');2-4)、分别用数值法和符号法求齐次微分方程在给定初始条件下的零输入响应波形,y′′(t)+2y(t)=0,y(0_)=3,y′(0_)=4。(注:题中时域范围可取[0 10],以实现方法作为图形标题名称)
% (1)数值法
a = [1 0 2]; % 方程左端系数向量
n=length(a)-1; % 微分方程的阶数(即根的数量)
Y0 = [3 4]; % 初始条件向量
p=roots(a); % 求特征方程的根
V=rot90(vander(p)); % 生成范德蒙特矩阵
C= V\Y0'; % 求对应于各特征根的系数 左除
dt = 0.1; tf = 10; % 时域取值范围[0 10]
t = 0:dt:tf; % 时域取值范围[0 10]
y = zeros(1,length(t));
for k=1:n y = y + C(k)*exp(p(k)*t); end % 将各分量叠加,得到零输入响应的通式
subplot(121);
plot(t, y), xlabel('t'), ylabel('real(y)'); %零输入响应的实部随时间变化的趋势
title('数值法');% 符号法
eq='D2y+2*y=0'; con='y(0)=3, Dy(0)=4';
y = dsolve(eq, con); y=simplify(y);
subplot(122);
ezplot(y, t); %一定要加参数t,限制时间的范围,保证波形正确
axis([0 10 -5 5]); % 限制xy轴范围
title('符号法'); 2-5)、求系统,y′(0+)=-1;y(0+)=0的全响应。(注:题中时域范围可取[0 10],参考函数tf2ss、lsim)
clear
b = [1]; a = [1 0 1];
t = 0:0.1:10; x = cos(t);
sys1 = tf(b,a); %系统函数模型
y1 = lsim(sys1,x,t); %零状态响应
% subplot(1,2,1),plot(t,y1);
xlabel('时间');title('零状态响应');
[A B C D] = tf2ss(b,a); %系统函数模型转化成状态空间模型参数
sys2 = ss(A,B,C,D) ;zi = [-1 0]; %产生状态空间模型和初始状态矩阵
y2 = lsim(sys2,x,t,zi); %全响应
% subplot(1,2,2);
plot(t,y2);
xlabel('时间t');title('全响应');
相关文章:

MATLAB连续LTI系统的时域分析(十)
目录 1、实验目的: 2、实验内容: 1、实验目的: 1)掌握利用MATLAB对系统进行时域分析的方法; 2)掌握连续时间系统零输入响应的求解方法; 3)掌握连续时间系统零状态响应、冲激响应和…...
HBuilderX使用
HBuilderX使用(Vue前后端分离) 概述:DCloud开发者后台 DAccount Service 1、官网下载开发工具:HBuilderX-高效极客技巧 注意:安装目录路径中不能出现中文特殊字符,否则会造成项目无法编译。比如C:/Progr…...
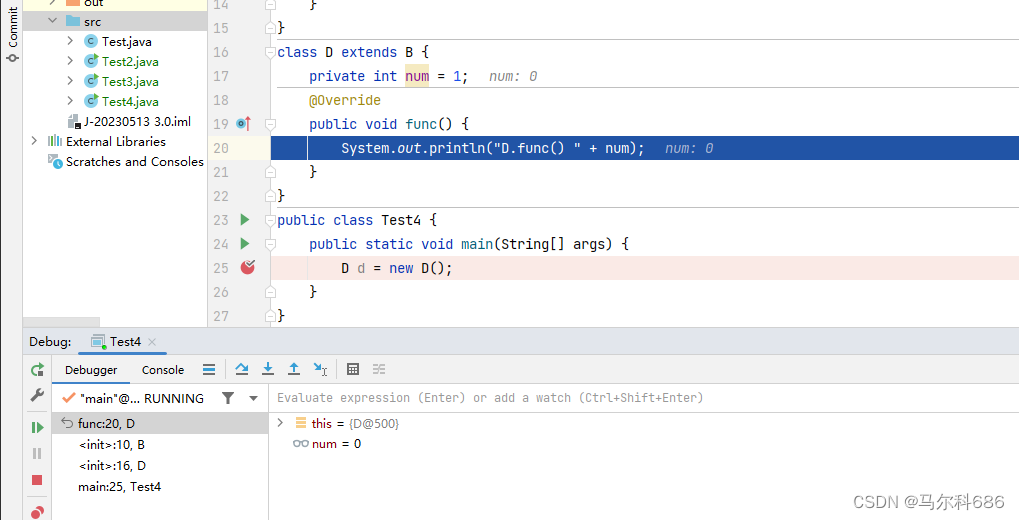
【JavaSE】多态(多态实现的条件 重写 向上转移和向下转型 向上转型 向下转型 多态的优缺点 避免在构造方法种调用重写的方法)
文章目录 多态多态实现的条件重写向上转移和向下转型向上转型向下转型 多态的优缺点避免在构造方法种调用重写的方法 多态 一种事物,多种形态。 多态的概念:去完成某个行为,当不同对象去完成时会产生出不同的状态。 多态实现的条件 1.必须…...
MySQL学习---13、存储过程与存储函数
1、存储过程概述 MySQL从5.0版本开始支持存储过程和函数。存储过程和函数能够将负杂的SQL逻辑封装在一起,应用程序无序关注存储过程和函数内部复杂的SQL逻辑,而只需要简单的调用存储过程和函数就可以。 1.1 理解 含义:存储过程的英文是Sto…...

Mysql日志管理、备份与恢复
文章目录 一、Mysql日志管理1.mysql日志2.日志种类3.日志的查询4.配置日志文件 二、Mysql备份与分类1.数据备份的重要性 一、Mysql日志管理 1.mysql日志 Mysql的日志默认保存位置为/usr/local/mysql/date,Mysql的日志配置文件为/etc/my.cnf,里面有一个…...

STM32单片机声控语音识别RGB彩灯多种模式亮度可调WS2812彩灯
实践制作DIY- GC0129-语音识别RGB彩灯 一、功能说明: 基于STM32单片机设计-语音识别RGB彩灯 二、功能介绍: STM32F103C系列最小系统板5VUSB电源64个灯珠的WS2812灯板1个开关键(3档亮度调节)1个模式切换键(白灯 红灯…...

高校9大学术工具推荐,一定要用起来哦!
1、文献管理工具:例如EndNote、Mendeley和Zotero,这些工具可以帮助您整理、管理和引用文献。 2、数据分析工具:例如SPSS、R和Python等,用于进行统计分析和数据处理。 3、学术写作工具:例如LaTeX和Microsoft Word&…...

记一次压力测试
性能测试文档 背景 为对产品性能有一定了解,现将产品展开一次性能测试; 环境与工具 本章为基本工具准备及linux命令说明,无先后顺序。 Xshell工具 本文使用Xshell在Windows界面下远程登录linux主机安装Xshell直接全部选择默认选项即可&…...

一个文明是否有竞争力,在很大程度上取决于信息传递的效率。
文章目录 引言I 有效地传递信息1.1 信息传播分类1.2 信息传递的有效性II 科技进步的必要条件和充分条件2.1 能量总量2.2 能量密度2.3 衡量科技成就的大小2.4 科学的诞生的意义:获得叠加式收益引言 科技进步的必要条件是能量总量,而充分条件是能量密度。一个文明是否有竞争力,…...

测试4年,跳槽一次涨8k,我跳了3次···
最近有人说,现在测试岗位初始工资太低了,有些刚刚入行的程序员朋友说自己工资连5位数都没有.....干了好几年也没怎么涨。看看别人动辄月薪2-3万,其实我想说也没那么难。说下如何高效地拿到3w。 1.暂且把刚入行的条件设低些吧,大专…...
Redis 入门教程(简单全面版)
1 安装: 1.1 生产环境安装 注意: 1、如果安装过程有问题可以参考源代码中的 README.md 文件 2、如果服务器只安装一个 redis 通常选择 /usr/local/redis 作为安装目录,如果安装多台则建议带上 服务名称 区分(建议带上 服务名称 区…...

java并发-AQS
当我们使用Java并发编程时,我们经常会听到“AQS”的概念。AQS代表“AbstractQueuedSynchronizer”,是Java并发包中的一个重要组件。AQS提供了一个框架,使得开发者可以轻松地实现各种同步器,例如锁,信号量,倒…...

openAI图像生成开发文档
图像生成 了解如何使用我们的 DALLE 型号 介绍 图像 API 提供了三种与图像交互的方法: 根据文本提示从头开始创建图像根据新的文本提示创建现有图像的编辑创建现有图像的变体 本指南介绍了使用这三个 API 终结点的基础知识以及有用的代码示例。要了解它们的实际…...

Python综合案例—利用tkinter实现计算器的程序
目录 一、导入 tkinter 库 定义全局变量 二、定义回调函数 三、创建窗口对象 四、创建标签控件 五、创建数字按钮 六、创建加、减、乘、除和等于按钮 七、创建清空按钮 八、总结 用Python实现计算器可以让我们更好地理解面向对象编程、GUI 编程和事件驱动编程等概念&a…...
canvas学习笔记
其实还有react还没有学,但是公司技术栈里面有canvas,所以先系统学习一下canvas 一、canvas 简介 <canvas> 是 HTML5 新增的,一个可以使用脚本(通常为 JavaScript) 在其中绘制图像的 HTML 元素。它可以用来制作照片集或者制作简单(也…...
Navicat Premium 15安装注教程
Navicat Premium 15安装 准备工作 下载好安装包navicat150_premium_cs_x64和安装完成Navicat Premium 15 链接:https://pan.baidu.com/s/1TJs3pjAXJXhu7-13DJLzpg 提取码:hunk 安装Navicat Premium 15 无脑操作,下一步下一步就行了&…...
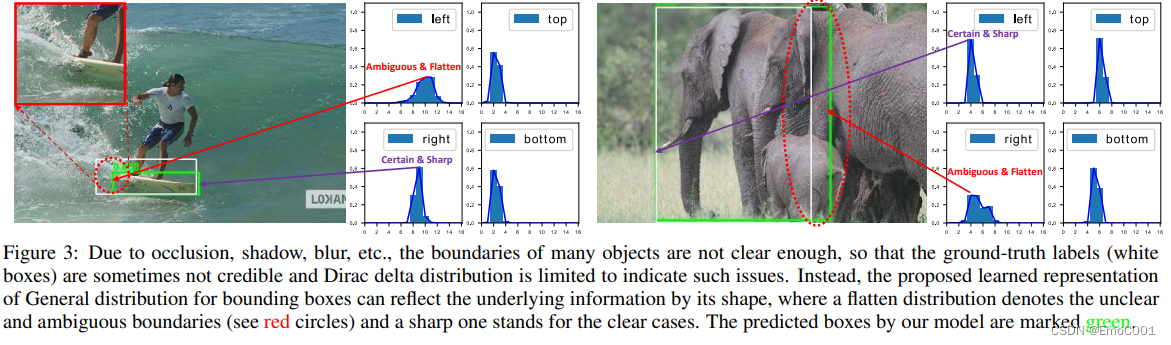
yolo v8
这个系列代码被封装的非常的精致,对二次开发不太友好,虽然也还是可以做些调节 模型的导出 有三种方式试过,都可以导出onnx的模型 1. 用yolov8 源码来自:ultralytics\yolo\engine\exporter.py (不固定尺寸) yolo export modelpa…...
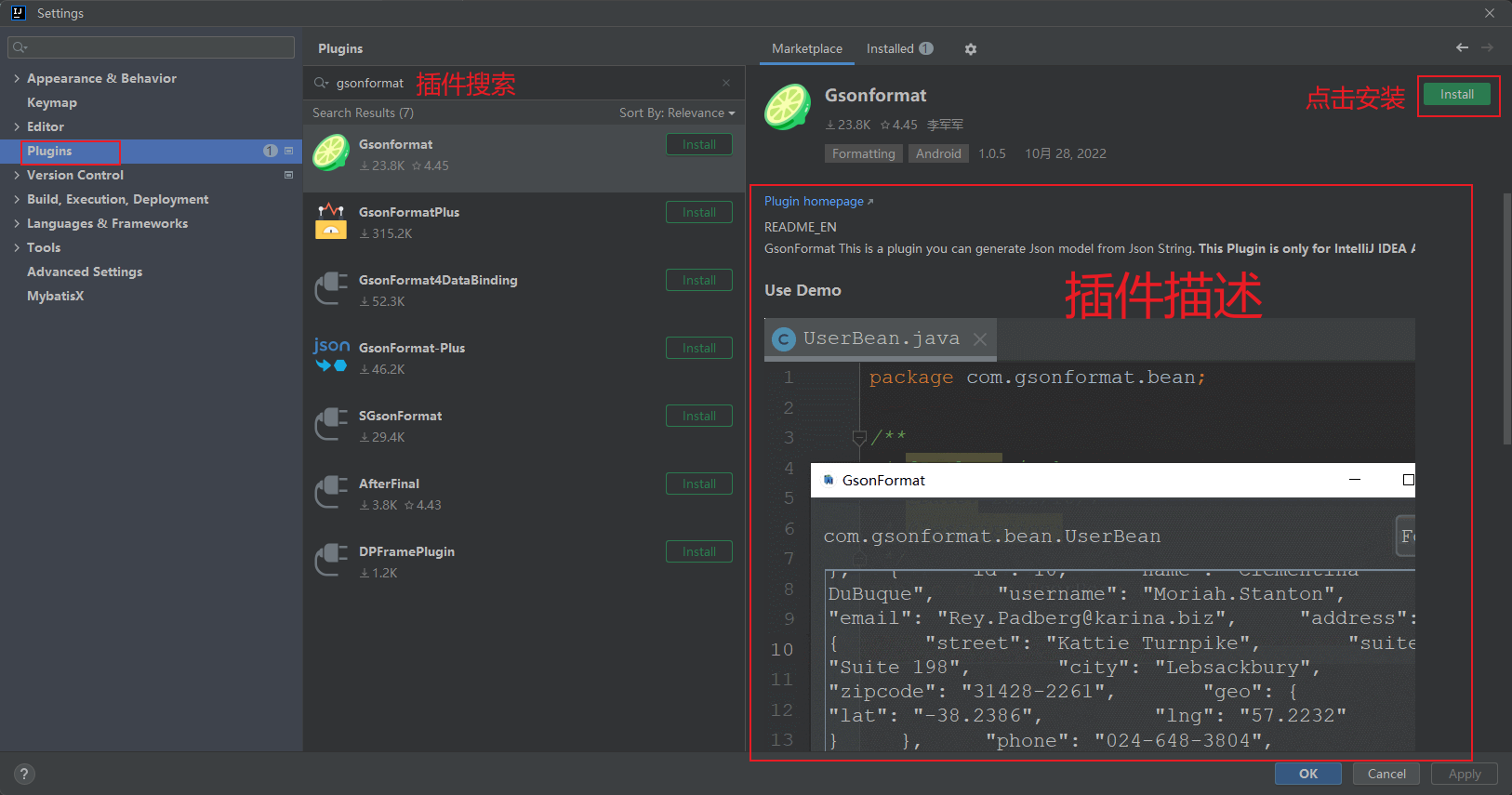
2022IDEA的下载、安装、配置与使用
文章目录 1.IntelliJ IDEA 介绍1.2 JetBrains 公司介绍1.2 IntelliJ IDEA 介绍1.3 IDEA 的主要功能介绍1.3.1 语言支持上1.3.2 其他支持 1.4 IDEA 的主要优势:(相较于 Eclipse 而言)1.5 IDEA 的下载地址1.6 官网提供的详细使用文档 2.windows 下安装过程2.1 安装前的…...
实验十 超市订单管理系统综合实验
实验十 超市订单管理系统综合实验 应粉丝要求,本博主帮助实现基本效果! 未避免产生版权问题,本项目博主不公开源码,如果您遇到相关问题可私聊博主! 一、实验目的及任务 通过该实验,掌握利用SSM框架进行系…...
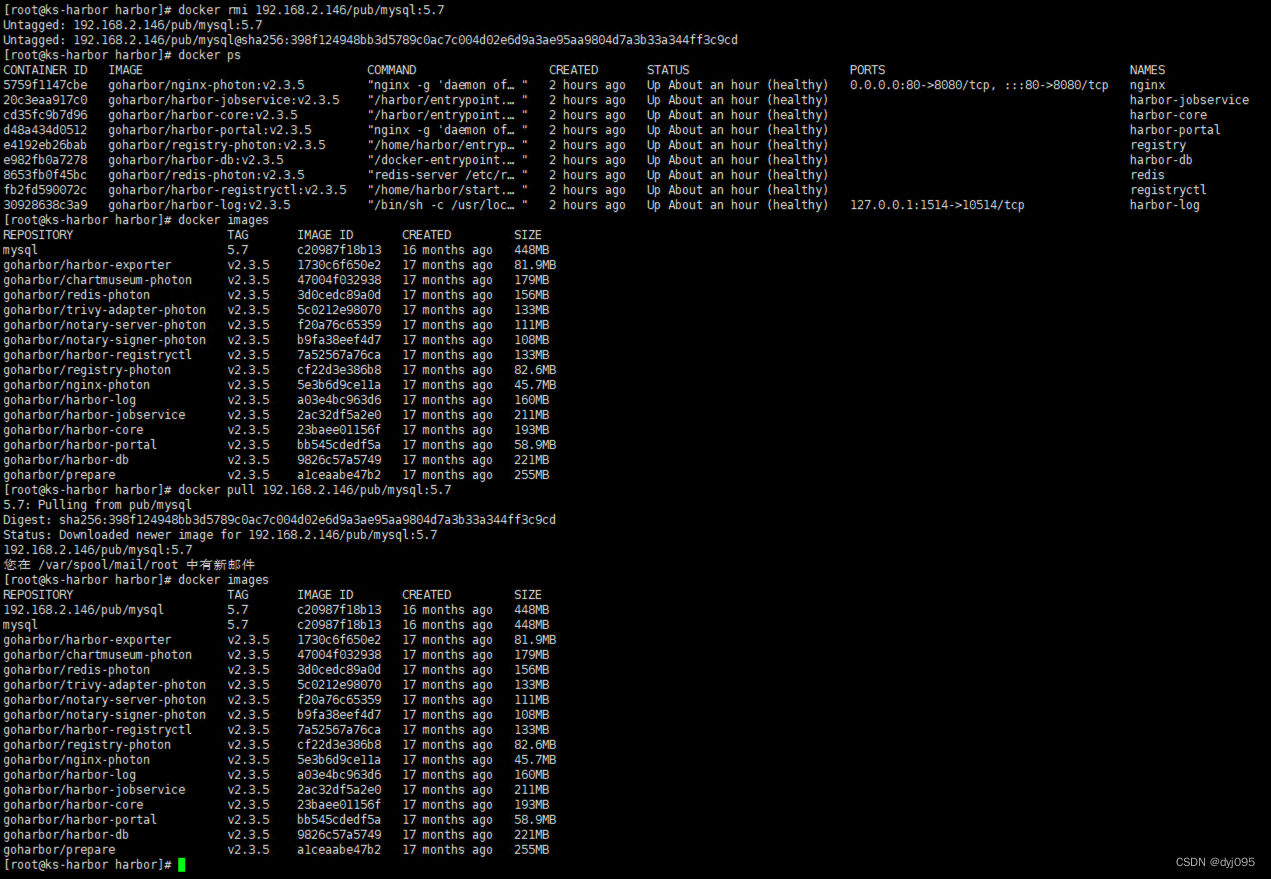
微服架构基础设施环境平台搭建 -(二)Docker私有仓库Harbor服务搭建
微服架构基础设施环境平台搭建 -(二)Docker私有仓库Harbor服务搭建 通过采用微服相关架构构建一套以KubernetesDocker为自动化运维基础平台,以微服务为服务中心,在此基础之上构建业务中台,并通过Jekins自动构建、编译、…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...



