牛客小白月赛 D.遗迹探险 - DP
题目描述
小Z是一名探险家。有一天,小Z误入了一个魔法遗迹。以下是该遗迹的具体组成:
1. 在 x 轴和 y 轴构成的平面上,满足在 1≤x≤n,1≤y≤m 的区域中(坐标(x,y)表示平面上的第x行的第y列),每个整数坐标 (x,y) 都有一个宝藏,坐标为(i,j)的宝藏的价值为ai,j(请注意,宝藏的价值可以为负)。换句话说,这个区域上的整点都有一个宝藏。
2. 对于任意一对点 (x1,y1) 和 (x2,y2),如果它们的横坐标相等,纵坐标之差为 1,则纵坐标小的点有一条道路可以到达纵坐标大的点,或者它们的纵坐标相等,横坐标之差为 1,则横坐标小的点有一条道路可以到达横坐标大的点。换句话说,(x,y)可以到达(x+1,y)或(x,y+1),反之不然。
3. 遗迹的入口在(1,1),出口在(n,m),小Z从入口进入后从出口离开,在移动的过程中他会将他所遇到的所有宝藏全部收集起来。
小Z想知道从进入到离开遗迹,他在离开遗迹时所能获得的宝藏的价值的和最大为多少。
作为一个有智慧的探险家,小Z当然会解决这个问题。但是由于这个遗迹具有魔法,问题就变得不是那么简单了。
在小Z进入该遗迹前,遗迹的魔法发动,它会在若干个具有宝藏的位置生成一个传送门。若小Z所在的坐标有传送门,则他可以通过这个传送门到达其它任意一个具有传送门的位置(当然,他也可以选择不使用传送门),并且小Z在使用一次传送门后,所有的传送门都会消失。换句话说,小Z只能最多使用一次传送门。
该遗迹具有魔法,每当小Z离开某个整点,该整点就会重新生成一个价值为ai,ja_{i,j}ai,j的宝藏。
小Z会进入TTT次该遗迹。请你帮助小Z计算出,对于每次进入遗迹,在给定传送门的坐标的情况下,他在离开遗迹时所能获得的宝藏的价值的和最大为多少?
输入描述:
第一行包含两个正整数 n,m (2≤n≤103),变量的含义如题意所示。接下来有n行,每行有m个整数,其中第i行第j列的数字代表坐标(i,j)的宝藏的价值ai,j (∣ai,j∣≤109)。接下来有一个数字T (1≤T≤103),表示小Z进入的遗迹次数。对于每次进入遗迹,第一行将给出一个整数k (2≤k≤5),表示传送门的个数。接下来k行,每行有两个整数x,y (1≤x≤n,1≤y≤m),表示坐标(x,y)上有一个传送门。 数据保证传送门的坐标两两不同。
输出描述:
输出T行,第i行表示第i次进入该遗迹的宝藏的最大值。
示例1
输入
3 3 1 2 3 4 5 6 7 8 9 2 2 1 1 3 3 3 1 1 1 3 3 1输出
58 41
分析:
计算两次dp,第一次计算从(1,1)到(i,j)的最大价值,第二次计算从(n,m)到(i,j)的最大价值(即任何一个点到(n,m)的最大价值),可以发现进入传送门可以多走一段路,那么最大价值就是不用传送门走到(n,m)的最大价值f(n,m),走到传送门的价值加上传送后(i,j)到(n,m)的最大值f(i1,j1)+g(i2,j2)。l另外需要预处理,注意存在负数情况。
代码:
#include <bits/stdc++.h>using namespace std;typedef pair<int,int> pii;
typedef long long ll;const int N=1010;ll a[N][N];
ll f[N][N];
ll g[N][N];int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,m;cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}memset(f,-0x3f,sizeof f);memset(g,-0x3f,sizeof g);f[0][1]=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];}}g[n][m+1]=0;for(int i=n;i>=1;i--){for(int j=m;j>=1;j--){g[i][j]=max(g[i+1][j],g[i][j+1])+a[i][j];}}int t;cin>>t;while(t--){vector<pii> d;int k;cin>>k;while(k--){int x,y;cin>>x>>y;d.push_back({x,y});}ll ans=f[n][m];for(int i=0;i<(int)d.size();i++){for(int j=0;j<(int)d.size();j++){if(i==j) continue;int x1=d[i].first;int x2=d[j].first;int y1=d[i].second;int y2=d[j].second;ans=max(ans,f[x1][y1]+g[x2][y2]);}}cout<<ans<<'\n';}
}相关文章:

牛客小白月赛 D.遗迹探险 - DP
题目描述 小Z是一名探险家。有一天,小Z误入了一个魔法遗迹。以下是该遗迹的具体组成: 1. 在 x 轴和 y 轴构成的平面上,满足在 1≤x≤n,1≤y≤m 的区域中(坐标(x,y)表示平面上的第x行的第y列),每个整数坐标 (x,y) 都有…...

前端架构师-week6-require源码解析
require 源码解析——彻底搞懂 npm 模块加载原理 require 的使用场景 加载模块类型 加载内置模块:require(fs)加载 node_modules 模块:require(ejs)加载本地模块:require(./utils)支持文件类型 加载 .js 文件加载 .mjs 文件加载 .json 文件…...

作为 IT 行业的过来人,你有什么话想对后辈说的?
作为 IT 行业的过来人,我想对后辈们说,要不断学习和探索新技术,但同时也要注意保持专注和耐心。在这个快速变化的时代,技术更新换代太快,可能会让人感到焦虑和无助,但只要有耐心并专注于自己所做的事情&…...
)
表数据编辑(数据库)
目录 一、插入数据 1.插入单个元组: INSERT…VALUES语句 2.插入子查询的结果: INSERT…SELECT语句 3.使用SELECT…INTO语句进行数据插入 二、修改数据 1、数据修改语句:UPDATE 2、修改给定表的所有行 3、基于给定表修改某…...
考虑多能负荷不确定性的区域综合能源系统鲁棒规划(Python代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
RocketMQ整理
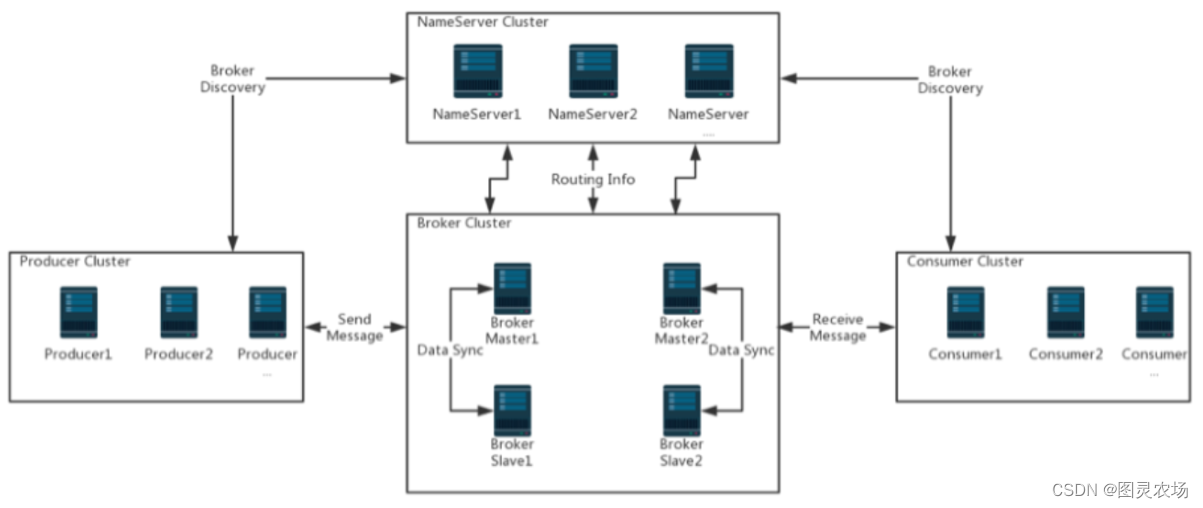
RocketMQ在阿里云上的商业版本,集成了阿里内部一些更深层次的功能及运维定制。开源版本,功能上略有缺失,但大体上是一样的。 使用Java开发,便于深度定制。最早叫MetaQ。消息吞吐量虽然依然不如Kafka,但是却比RabbitMQ高很多。在阿里内部,RocketMQ集群每天处理的请求数超过…...

Springboot +Flowable,会签、或签简单使用(二)
一.简介 **会签:**在一个流程中的某一个 Task 上,这个 Task 需要多个用户审批,当多个用户全部审批通过,或者多个用户中的某几个用户审批通过,就算通过。 例如:之前的请假流程,假设这个请假流程…...
将核心交换机配置为NTP服务器
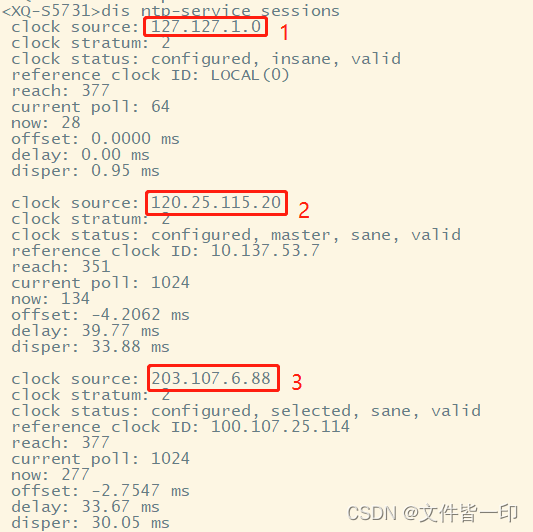
AR配置外源NTP 1.配置ntp <XQ-R1220>sys [XQ-R1220]ntp-service unicast-server 120.25.115.20 #阿里云ntp [XQ-R1220]ntp-service unicast-server 203.107.6.88 #阿里云ntp 2.查看ntp状态 <XQ-R1220>display ntp status clock sta…...

application.properties文件注释
这是一个常用的Spring Boot配置文件 在这里,我们可以配置应用程序的各种属性 服务器端口号 server.port8080 数据库配置 spring.datasource.urljdbc:mysql://localhost:3306/test spring.datasource.usernameroot spring.datasource.password123456 spring.datasou…...

MySql查询报错this is incompatible with sql_mode=only_full_group_by
错误示例 Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column ‘yiliaohaocai_new.a.id’ which is not functionally dependent on columns in GROUP BY clause; this is incompatible with sql_modeonly_full_group_by 原因 SQL …...
VMware Workstation 网络备忘 + 集群规模
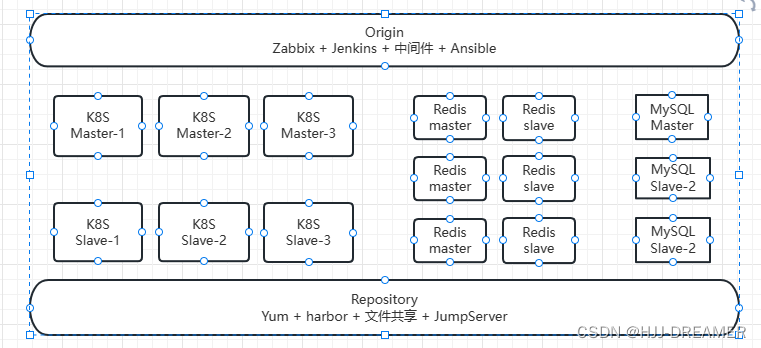
概述 在虚拟机中部署服务,进行IP规划,进行相关的前期准备 3 张网卡 2个不同的网段 1个NAT 概述截图 NAT 截图 VMnet0 截图 VMnet1 截图 总结: 网卡(网络适配器)名称IP网段备注NATens33192.168.139.0VMnet0ens34VMne…...

被裁现状,给找工作的同学一些建议
2022 到 2023 国内知名互联网公司腾讯、阿里、百度、快手、滴滴、京东、阿里、爱奇艺、知乎、字节跳动、小米等公司均有裁员,其中有不少公司,在过去年的一整年,进行了多轮裁员,以下是网传的一张 “2022 年裁员企业名单”。 这些裁…...

编程到底难在哪里?
编程是一门非常有挑战性的技术,能够让人们使用计算机来完成各种任务。它不仅需要掌握各种计算机语言和框架,还需要在实际应用中充分发挥自己的专业知识和创造力。 然而,对于初学者来说,在编程过程中遇到的难点可能是多方面的。以…...

C++ 仿函数(一)
目录 一、仿函数是什么? 二、仿函数的特点 1.仿函数在使用时,可以像普通函数那样调用, 可以有参数,可以有返回值 2.仿函数超出普通函数的概念,可以有自己的状态 编辑3.仿函数可以作为参数传递。 三、谓词 一元谓词示例&a…...

MATLAB连续LTI系统的时域分析(十)
目录 1、实验目的: 2、实验内容: 1、实验目的: 1)掌握利用MATLAB对系统进行时域分析的方法; 2)掌握连续时间系统零输入响应的求解方法; 3)掌握连续时间系统零状态响应、冲激响应和…...
HBuilderX使用
HBuilderX使用(Vue前后端分离) 概述:DCloud开发者后台 DAccount Service 1、官网下载开发工具:HBuilderX-高效极客技巧 注意:安装目录路径中不能出现中文特殊字符,否则会造成项目无法编译。比如C:/Progr…...
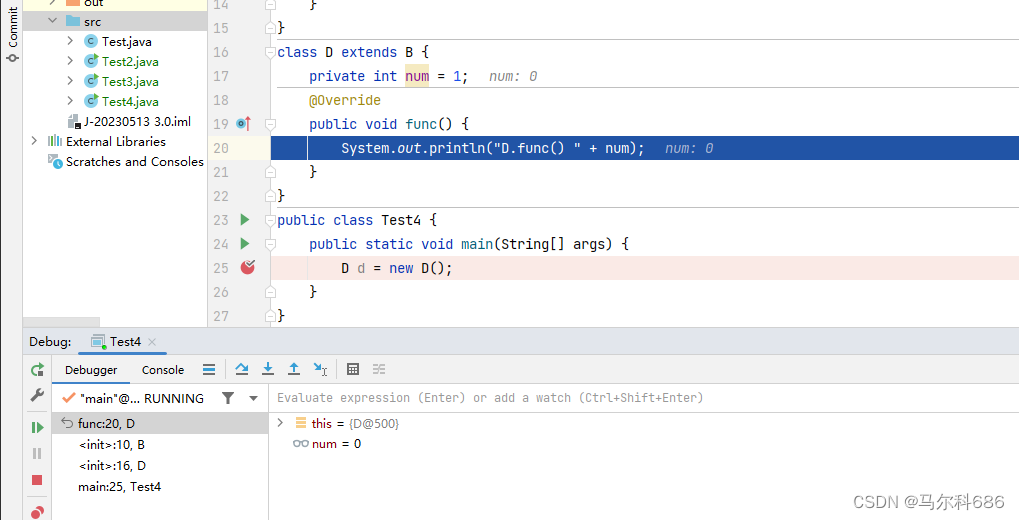
【JavaSE】多态(多态实现的条件 重写 向上转移和向下转型 向上转型 向下转型 多态的优缺点 避免在构造方法种调用重写的方法)
文章目录 多态多态实现的条件重写向上转移和向下转型向上转型向下转型 多态的优缺点避免在构造方法种调用重写的方法 多态 一种事物,多种形态。 多态的概念:去完成某个行为,当不同对象去完成时会产生出不同的状态。 多态实现的条件 1.必须…...
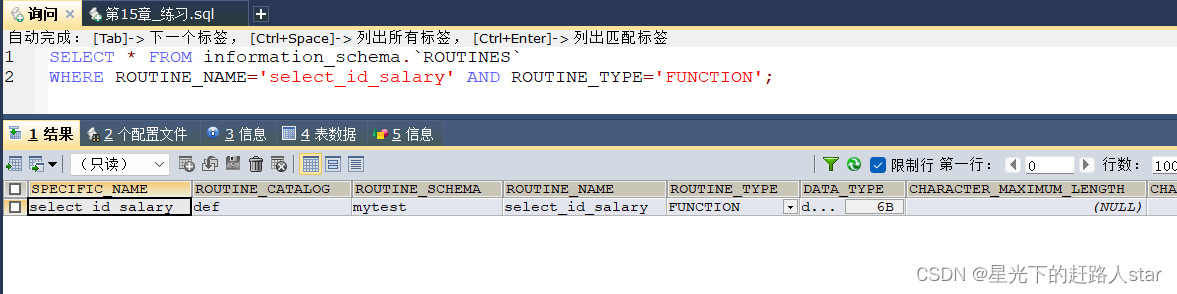
MySQL学习---13、存储过程与存储函数
1、存储过程概述 MySQL从5.0版本开始支持存储过程和函数。存储过程和函数能够将负杂的SQL逻辑封装在一起,应用程序无序关注存储过程和函数内部复杂的SQL逻辑,而只需要简单的调用存储过程和函数就可以。 1.1 理解 含义:存储过程的英文是Sto…...

Mysql日志管理、备份与恢复
文章目录 一、Mysql日志管理1.mysql日志2.日志种类3.日志的查询4.配置日志文件 二、Mysql备份与分类1.数据备份的重要性 一、Mysql日志管理 1.mysql日志 Mysql的日志默认保存位置为/usr/local/mysql/date,Mysql的日志配置文件为/etc/my.cnf,里面有一个…...

STM32单片机声控语音识别RGB彩灯多种模式亮度可调WS2812彩灯
实践制作DIY- GC0129-语音识别RGB彩灯 一、功能说明: 基于STM32单片机设计-语音识别RGB彩灯 二、功能介绍: STM32F103C系列最小系统板5VUSB电源64个灯珠的WS2812灯板1个开关键(3档亮度调节)1个模式切换键(白灯 红灯…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
