【一起啃书】《机器学习》第五章 神经网络
文章目录
- 第五章 神经网络
- 5.1 神经元模型
- 5.2 感知机与多层网络
- 5.3 误差逆传播算法
- 5.4 全局最小与局部极小
- 5.5 其他常见神经网络
- 5.6 深度学习
第五章 神经网络
5.1 神经元模型
神经网络是由具有适应性简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应,神经网络中最基本的成分是神经元模型,以下为第一个神经元数学模型——M-P神经元模型。

在这个模型中,神经元接收到来自 n n n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过“激活函数”处理以产生神经元的输出,理想中的激活函数如下图a所示的阶跃函数,它将输入值映射为输出值“0”或“1”,其中“1”对应于神经元兴奋,“0”对应于神经元抑制。

然而,阶跃函数具有不连续、不光滑等不太好的性质,所以实际常用Sigmoid函数作为激活函数。目前常用的激活函数主要有以下几种,具体的可以参考这个链接(激活函数 | 深度学习领域最常用的10个激活函数,详解数学原理及优缺点)。
- 线性激活函数:输出与输入成正比,没有非线性特性,一般用于输出层。
- Sigmoid激活函数:输出在0到1之间,具有平滑的非线性特性,一般用于二分类问题或者概率输出。
- 双曲正切激活函数:输出在-1到1之间,具有平滑的非线性特性,一般用于多分类问题或者中心化输出。
- ReLU激活函数:输出为0或者正数,具有分段的非线性特性,一般用于隐藏层,可以加速收敛和减少梯度消失。
- Leaky ReLU激活函数:输出为负数或者正数,具有分段的非线性特性,一般用于隐藏层,可以避免ReLU的死亡节点问题。
- ELU激活函数:输出为负指数或者正数,具有平滑的非线性特性,一般用于隐藏层,可以避免ReLU的死亡节点问题,并且有更好的收敛效果。
- SELU激活函数:输出为负指数或者正数,具有平滑的非线性特性,一般用于隐藏层,可以自动归一化网络,并且有更好的收敛效果。
- Swish激活函数:输出为负数或者正数,具有平滑的非线性特性,一般用于隐藏层,可以提高准确率和稳定性。
- Softmax激活函数:输出为多个0到1之间的值,其和为1,具有平滑的非线性特性,一般用于输出层,可以表示多分类问题的概率分布。
5.2 感知机与多层网络
感知机是神经网络最基本的模型,它是由一个或多个神经元组成的,而神经网络是由多个感知机或其他类型的神经元连接而成的复杂模型,它可以实现非线性分类和回归等功能,比如下面就是一个有两个输入神经元的感知机网络结构 y = f ( ∑ w i x i − θ ) y = f(\sum {{w_i}} {x_i} - \theta ) y=f(∑wixi−θ),可以实现与、或、非运算。
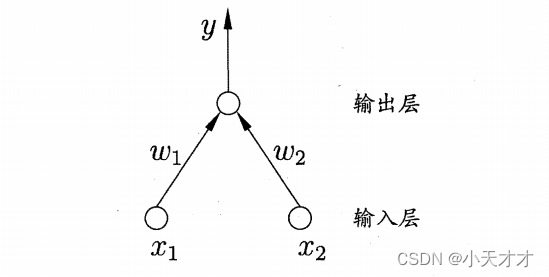
更一般的,给定训练数据集,权重 w w w以及阈值 θ \theta θ可以通过学习得到,而阈值 θ \theta θ可以看作固定输入为-1的权重 w n + 1 w_{n+1} wn+1,这样就可以统一为权重的学习,对于感知机来说,学习规则如下所示,假设当前感知机的输出为$\mathop y\limits^ \wedge $,感知机权重将这样调整:
w i ← w i + Δ w i Δ w i = η ( y − y ∧ ) x i {w_i} \leftarrow {w_i} + \Delta {w_i}\\ \Delta {w_i} = \eta (y - \mathop y\limits^ \wedge ){x_i} wi←wi+ΔwiΔwi=η(y−y∧)xi
其中 η ∈ ( 0 , 1 ) \eta \in (0,1) η∈(0,1)称为学习率,若感知机预测正确,则感知机不发生变化,否则将根据错误的程度进行权重调整,这也是感知机学习算法,是一种基于误分类的监督学习算法,目标是找到一个能够将训练数据正确分类的超平面。
感知机选择将预测值与实际值作差的形式来进行权重更新的依据是为了使超平面向正确分类的方向移动。当一个实例被误分类时,预测值与实际值的差就是误差的符号,它表示了超平面与实例之间的距离和方向,此时将误差乘以输入向量,就可以得到一个调整量,它表示了超平面在每个特征维度上需要移动的大小和方向,而将调整量加到权重上,就可以使超平面向正确分类的方向移动一定的距离。这样,经过多次迭代,超平面就可以逐渐接近最优的位置了。
上述问题都是线性可分问题,而这样的感知机无法解决非线性可分问题,要解决非线性可分问题,需要考虑使用多层功能神经元。如下所示的两层感知机,就可以解决异或问题,而在输出层与输入层之间的一层神经元则被称为隐层或隐含层,也是具有激活函数的功能神经元。
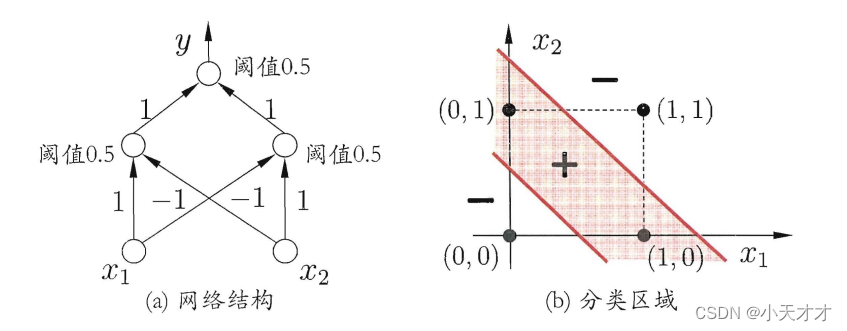
下面介绍一下前馈神经网络,在前馈神经网络中,每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接,如下所示:
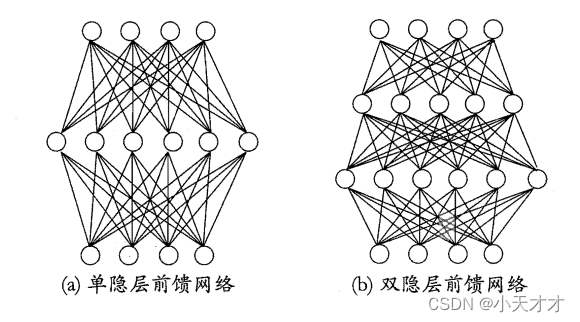
前馈神经网络与反馈神经网络的区别:深度学习–前馈神经网络、反馈神经网络
5.3 误差逆传播算法
多层网络的学习能力比单层感知器强得多,如果想训练多层网络,上述简单感知器的学习规则显然就不够了,需要更强大的学习算法,下面来介绍一下BP算法,BP算法是一种用于训练多层神经网络的梯度下降算法,它利用链式法则计算网络每层的权重对损失函数的梯度,然后更新权重来最小化损失函数。BP算法分为两个阶段:激励传播和权重更新。激励传播阶段包括前向传播和反向传播,前向传播是将训练输入送入网络以获得预测结果,反向传播是计算预测结果与训练目标的误差。权重更新阶段是根据误差和梯度调整网络的权重,以减小误差。
下面对BP算法中的一些符号进行定义,以一个拥有 d d d个输入神经元、 l l l个输出神经元、 q q q个隐层神经元的多层前馈网络结构为例,假设隐层和输出层神经元都是用Sigmoid函数作为激活函数。
- D D D:训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , x i ∈ R d , y ∈ R l D = \{ ({x_1},{y_1}),({x_2},{y_2}),...,({x_m},{y_m})\} ,{x_i} \in {{ R}^d},y \in {{ R}^l} D={(x1,y1),(x2,y2),...,(xm,ym)},xi∈Rd,y∈Rl,即输入示例由 d d d个属性描述,输出 l l l维实值向量
- θ j {\theta _j} θj:输出层第 j j j个神经元的阈值
- γ h {\gamma _h} γh:隐层第 h h h个神经元的阈值
- v i h {v_{ih}} vih:输入层第 i i i个神经元与隐层第 h h h个神经元之间的连接权重
- w h j {w_{hj}} whj:隐层第 h h h个神经元与输出层第 j j j个神经元之间的连接权重
- α h {\alpha _h} αh:隐层第 h h h个神经元接收到的输入 α h = ∑ i = 1 d v i h x i {\alpha _h} = \sum\limits_{i = 1}^d {{v_{ih}}{x_i}} αh=i=1∑dvihxi
- β j {\beta _j} βj:输出层第 j j j个神经元接收到的输入 β j = ∑ h = 1 q w h j b h {\beta _j} = \sum\limits_{h = 1}^q {{w_{hj}}} {b_h} βj=h=1∑qwhjbh,其中 b h b_h bh为隐层第 h h h个神经元的输出

对于训练例 ( x k , y k ) ({x_k},{y_k}) (xk,yk),假定神经网络的输出为 y ∗ k = ( y ∗ 1 k , y ∗ 2 k , . . . , y ∗ l k ) {{y^*}_k} = ({y^*}_1^k,{y^*}_2^k,...,{y^*}_l^k) y∗k=(y∗1k,y∗2k,...,y∗lk),即 y ∗ l k = f ( β j − θ j ) {y^*}_l^k = f({\beta _j} - {\theta _j}) y∗lk=f(βj−θj),则网络在 ( x k , y k ) ({x_k},{y_k}) (xk,yk)上的均方误差为
E k = 1 2 ∑ j = 1 l ( y ∗ l k − y j k ) 2 {E_k} = \frac{1}{2}{\sum\limits_{j = 1}^l {({y^*}_l^k - y_j^k)} ^2} Ek=21j=1∑l(y∗lk−yjk)2
下面以隐层到输出层的连接权重 w h j w_{hj} whj为例来进行权重更新的推导,对于误差 E k E_k Ek,给定学习率 η \eta η,有
Δ w h j = − η ∂ E k ∂ w h j ∂ E k ∂ w h j = ∂ E k ∂ y ∗ l k ⋅ ∂ y ∗ l k ∂ β j ⋅ ∂ β j ∂ w h j , ∂ β j ∂ w h j = b h \Delta {w_{hj}} = - \eta \frac{{\partial {E_k}}}{{\partial {w_{hj}}}}\\ \frac{{\partial {E_k}}}{{\partial {w_{hj}}}} = \frac{{\partial {E_k}}}{\partial {y^*}_l^k} \cdot \frac{\partial {y^*}_l^k}{{\partial {\beta _j}}} \cdot \frac{{\partial {\beta _j}}}{{\partial {w_{hj}}}}, \frac{{\partial {\beta _j}}}{{\partial {w_{hj}}}} = {b_h} Δwhj=−η∂whj∂Ek∂whj∂Ek=∂y∗lk∂Ek⋅∂βj∂y∗lk⋅∂whj∂βj,∂whj∂βj=bh
Sigmoid函数有一个很好的性质: f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x) = f(x)(1 - f(x)) f′(x)=f(x)(1−f(x)),所以可以定义如下 g j g_j gj:
g j = − ∂ E k ∂ y ∗ l k ⋅ ∂ y ∗ l k ∂ β j = − ( y ∗ l k − y j k ) f ′ ( β j − θ j ) = y ∗ l k ( 1 − y ∗ l k ) ( y j k − y ∗ l k ) {g_j} = - \frac{{\partial {E_k}}}{\partial {y^*}_l^k} \cdot \frac{\partial {y^*}_l^k}{{\partial {\beta _j}}} = - ({y^*}_l^k - y_j^k)f'({\beta _j} - {\theta _j}) = {y^*}_l^k(1 - {y^*}_l^k)(y_j^k - {y^*}_l^k) gj=−∂y∗lk∂Ek⋅∂βj∂y∗lk=−(y∗lk−yjk)f′(βj−θj)=y∗lk(1−y∗lk)(yjk−y∗lk)
将上述 g j g_j gj代入之前的式子即可得到权重 w h j w_{hj} whj的更新公式: Δ w h j = η g j b h \Delta {w_{hj}} = \eta g_j b_h Δwhj=ηgjbh,类似也可以得到其他权重的更新公式,如下所示:
Δ θ j = − η g j , Δ v i h = η e h x i , Δ γ h = − η e h 其中 e h = − ∂ E k ∂ b h ⋅ ∂ b h ∂ α h = − ∑ j = 1 l ∂ E k ∂ β j ⋅ ∂ β j ∂ b h f ′ ( α h − γ h ) = ∑ j = 1 l w h j g j f ′ ( α h − γ h ) = b h ( 1 − b h ) ∑ j = 1 l w h j g j \Delta {\theta _j} = - \eta {g_j},\Delta {v_{ih}} = \eta {e_h}{x_i},\Delta {\gamma _h} = - \eta {e_h}\\ 其中{e_h} = - \frac{{\partial {E_k}}}{{\partial {b_h}}} \cdot \frac{{\partial {b_h}}}{{\partial {\alpha _h}}} = - \sum\limits_{j = 1}^l {\frac{{\partial {E_k}}}{{\partial {\beta _j}}} \cdot \frac{{\partial {\beta _j}}}{{\partial {b_h}}}} f'({\alpha _h} - {\gamma _h}) = \sum\limits_{j = 1}^l {{w_{hj}}} {g_j}f'({\alpha _h} - {\gamma _h}) = {b_h}(1 - {b_h})\sum\limits_{j = 1}^l {{w_{hj}}} {g_j} Δθj=−ηgj,Δvih=ηehxi,Δγh=−ηeh其中eh=−∂bh∂Ek⋅∂αh∂bh=−j=1∑l∂βj∂Ek⋅∂bh∂βjf′(αh−γh)=j=1∑lwhjgjf′(αh−γh)=bh(1−bh)j=1∑lwhjgj
下面给出BP算法的工作流程,对于每个训练样例,BP算法执行以下操作:先将输入示例提供给输入层神经元,然后逐层将信号前传,直到产生输出层的结果;然后计算输出层的误差,再将误差逆向传播至隐层神经元,最后根据隐层神经元的误差来对连接权重和阈值进行调整。该迭代过程循环进行,直到达到某些停止条件为止,比如训练误差已达到一个很小的值。

BP算法的目标是要最小化训练集 D D D上的累积误差 E = 1 m ∑ k = 1 m E k E = \frac{1}{m}\sum\limits_{k = 1}^m {{E_k}} E=m1k=1∑mEk,在这里要注意虽然BP算法里面有反向传播这一步,但这与反馈神经网络中的反馈是不同的,BP算法里面的反向传播是指根据网络的输出误差,从输出层到输入层逐层计算并更新权重参数的过程,而反馈神经网络中的反馈是指网络的输出会经过一定的变换后,再作为输入传回到网络中,形成一个循环或回路。
下面介绍一下两种BP算法:标准BP算法与累积BP算法。
标准BP算法每次只针对一个训练样例更新参数,也就是随机梯度下降法(stochastic gradient descent),优点是参数更新频繁,可以加快收敛速度和避免局部最优,缺点是参数更新不一致,可能导致震荡和偏离最优方向。累积BP算法每次针对所有训练样例更新参数,也就是批量梯度下降法(batch gradient descent),优点是参数更新稳定,可以减少噪声和波动,缺点是参数更新缓慢,可能导致陷入局部最优或过拟合。比如,假设有n个训练样例,分别使用标准BP和累积BP,那么参数更新的次数取决于迭代轮数,假设迭代轮数为m,那么:
- 标准BP算法每轮迭代会对每个训练样例进行一次参数更新,所以总共会进行m*n次参数更新。
- 累积BP算法每轮迭代会对所有训练样例进行一次参数更新,所以总共会进行m次参数更新。
为了缓解BP网络的过拟合,一共有两种策略——早停和正则化。早停是将数据集分成训练集和验证集,训练集用来计算梯度、更新连接权重和阈值,验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权重和阈值。正则化是在误差目标函数中增加一个用于描述网络复杂度的部分,比如连接权重与阈值的平方和。
5.4 全局最小与局部极小
在神经网络的训练过程中,我们往往会谈到两种最优:局部极小与全局最小。显然,参数空间内梯度为零的点,只要其误差函数值小于邻点的误差函数值,就是局部极小点;可能存在多个局部极小值,但是却只会有一个全局最小值。
基于梯度的搜索时使用最为广泛的参数寻优方法,梯度下降法是沿着负梯度方向搜索最优解,因为负梯度方向是函数在当前点的方向导数最小的方向,方向导数是函数沿着某个方向的变化率,它与函数的梯度和该方向的单位向量的点积相等,当两个向量的夹角为180度时,点积最小,也就是说,当单位向量与梯度的反方向一致时,方向导数最小。因此,沿着负梯度方向走,函数值下降最快。

目前常采用以下策略来试图跳出局部极小,从而进一步接近全局最小:
- 以多组不同参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数,这相当于从多个不同的初始点开始搜索,这样就可能陷入不同的局部极小,从中进行选择有可能获得更接近全局最小的结果。
- 使用“模拟退火”技术。模拟退火在每一步都以一定的概率接受比当前解更差的结果,从而有助于“跳出”局部极小。在每步迭代过程中,接受“次优解”的概率要随着时间的推移而逐渐降低,从而保证算法稳定。
- 使用随机梯度下降。与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素。于是,即便陷入局部极小点,它计算出的梯度仍可能不为零,这样就有机会跳出局部极小继续搜索。
5.5 其他常见神经网络
(1)RBF网络
RBF网络是一种单隐层前馈神经网络,它使用径向基函数作为隐层神经元的激活函数,而输出层则是对隐层神经元输出的线性组合。
(2)ART网络
竞争型学习是神经网络中一种常用的无监督学习策略,在使用该策略时,网络的输出神经元相互竞争,每一时刻仅有一个竞争获胜的神经元被激活,其他神经元的状态被抑制。而ART网络是竞争型学习的重要代表,该网络由比较层、识别层、识别阈值和重置模块组成。
在接收到比较层的输入信号后,识别层神经元之间相互竞争以产生获胜神经元,竞争的最简单方式是,计算输入向量与每个识别层神经元所对应的模式类的代表向量之间的距离,距离最小者胜。获胜神经元将向其他识别层神经元发送信号,抑制其激活。若输入向量与获胜神经元所对应的代表向量之间的相似度大于识别阈值,则当前输入样本将被归为该代表向量所属类别,同时,网络连接权重将会更新,使得以后在接收到相似输入样本时该模式类会计算出更大的相似度,从而使该获胜神经元有更大可能获胜;若相似度不大于识别阈值,则重置模块将在识别层增设一个新的神经元,其代表向量就设置为当前输入向量。
(3)SOM网络
SOM网络是一种竞争学习型的无监督神经网络,它能将高维输入数据映射到低维空间,同时保持输入数据在高维空间的拓扑结构,即将高维空间中相似的样本点映射到网络输出层中的邻近神经元。
如下图所示,SOM网络中的输出层神经元以矩阵方式排列在二维空间中,每个神经元都拥有一个权向量,网络在接收输入向量后,将会确定输出层获胜神经元,它决定了该输入向量在低维空间中的位置。SOM的训练目标就是为每个输出层神经元找到合适的权向量,以达到保持拓扑结构的目的。
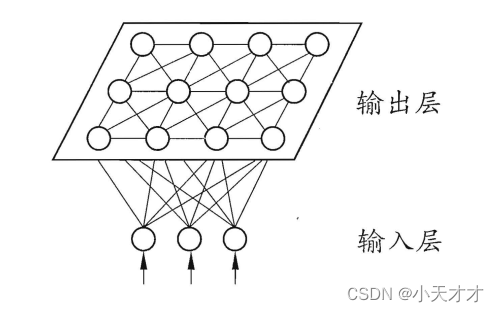
(4)级联相关网络
一般的神经网络模型通常假定网络结构是事先固定的,训练的目的是利用训练样本来确定合适的连接权重、阈值等参数。与此不同,结构自适应网络则将网络结构也当作学习的目标之一,并希望能在训练过程中找到最符合数据特点的网络结构,级联相关网络是结构自适应网络的重要代表。
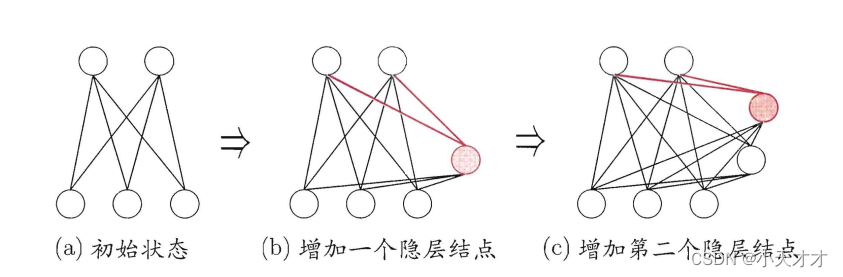
级联相关网络有两个主要成分:“级联”和“相关”。级联是指建立层次连接的层级结构,相关是指通过最大化新神经元的输出与网络误差之间的相关性来训练相关的参数。
(5)Elman网络
Elman网络是最常用的递归神经网络之一,如下所示,它的结构与多层前馈网络很相似,但隐层神经元的输出被反馈回来,与下一时刻输入层神经元提供的信号一起,作为隐层神经元在下一时刻的输入。隐层神经元通常采用Sigmoid激活函数,而网络的训练则常通过推广的BP算法进行。
5.6 深度学习
典型的深度学习模型就是很深层的神经网络,深度学习有很多应用场景,例如:
- 语音识别:深度学习可以用于语音识别、语音合成等任务,例如谷歌的语音助手、苹果的Siri等。
- 图像识别:深度学习在图像分类、目标检测、图像语义分割等计算机视觉任务中取得了显著成果,例如谷歌的人脸识别、腾讯的美颜相机等。
- 自然语言处理:深度学习可以用于文本生成、机器翻译、情感分析等自然语言处理任务,例如微软的小冰、百度的翻译等。
- 游戏:深度学习可以用于强化学习,让机器自主地学习和优化策略,例如谷歌的AlphaGo、OpenAI的Dota 2机器人等。
- 医疗:深度学习可以用于医疗图像分析、疾病诊断、药物发现等医疗领域,例如IBM的Watson、阿里的ET医疗大脑等。
- 艺术:深度学习可以用于图像风格迁移、图像生成、音乐生成等艺术领域,例如谷歌的Deep Dream、Prisma等。
以下是卷积神经网络用于手写数字识别的一个例子。

相关文章:

【一起啃书】《机器学习》第五章 神经网络
文章目录 第五章 神经网络5.1 神经元模型5.2 感知机与多层网络5.3 误差逆传播算法5.4 全局最小与局部极小5.5 其他常见神经网络5.6 深度学习 第五章 神经网络 5.1 神经元模型 神经网络是由具有适应性简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统…...
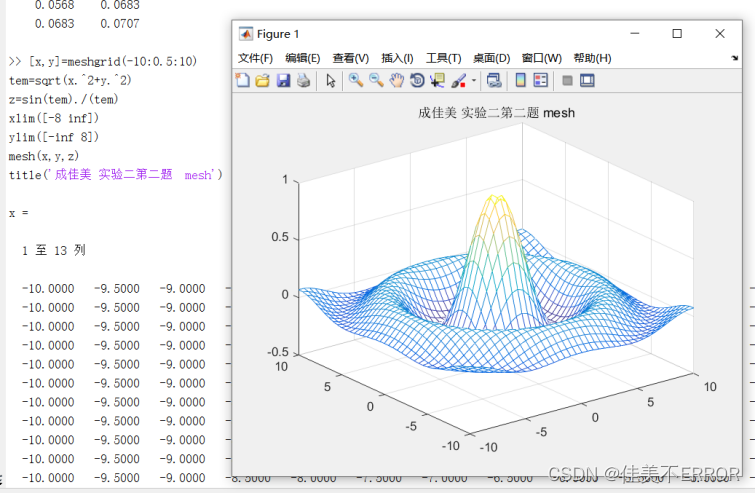
matlab实验二可视化
学聪明点,自己改,别把我卖了 一、实验目的及要求 要求 1、掌握 MATLAB常用的二维和三维绘图函数 2、掌握MATLAB的图形注释 3、熟悉MATLAB常用的图形修饰 4、熟悉MATLAB的图形动画 实验原理 1、MATLAB二维绘图:plot,fplot,fimplicit…...
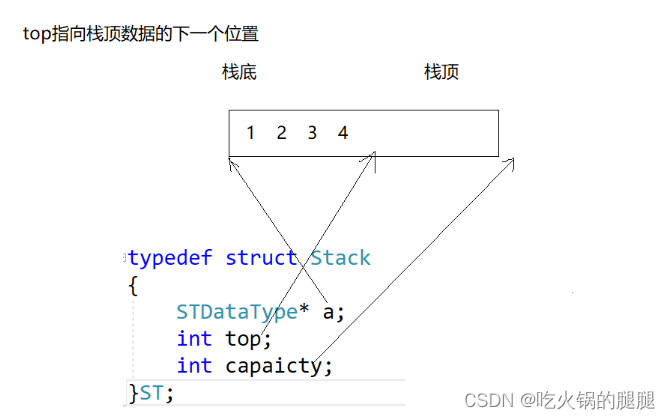
(数据结构)栈的实现——再一次保姆级教学
目录 1. 栈 编辑 1.2 栈的实现 2. 代码的实现 2.1 初始化栈和销毁栈 2.2栈顶元素的插入 2.3栈顶元素的删除 栈元素删除 2.4栈顶元素的获取和栈元素的个数 1. 栈 1.1 栈的概念和结构 栈(Stack)是一种线性存储结构,它具有如下特点: ࿰…...

【5G RRC】RSRP、RSRQ以及SINR含义、计算过程详细介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

K8s(Kubernetes)学习(一):k8s概念及组件
Kubernetes中文文档:https://kubernetes.io/zh-cn/docs/home/ Kubernetes源码地址:https://github.com/kubernetes/kubernetes 一:Kubernetes是什么 首先要了解应用程序部署经历了以下几个时代: 传统部署时代:在物理服务器上运…...

Web3 常用语和黑话你知道吗?
My friend Dave used to be a bagholder, but he FOMO’d and bought even more BTC. Now, he’s a big whale HODLing for that moon. …that’s a lot to take in for just two sentences. If you’re new to Bitcoin and the world of cryptocurrencies, we understand if …...

物联网和边缘计算:如何将数据处理和决策推向设备边缘
第一章:引言 当我们谈论物联网(IoT)时,我们通常指的是将各种设备连接到互联网,并通过数据交换来实现智能化的网络。然而,传统的物联网模型通常涉及将数据发送到云端进行处理和分析。然而,随着技…...
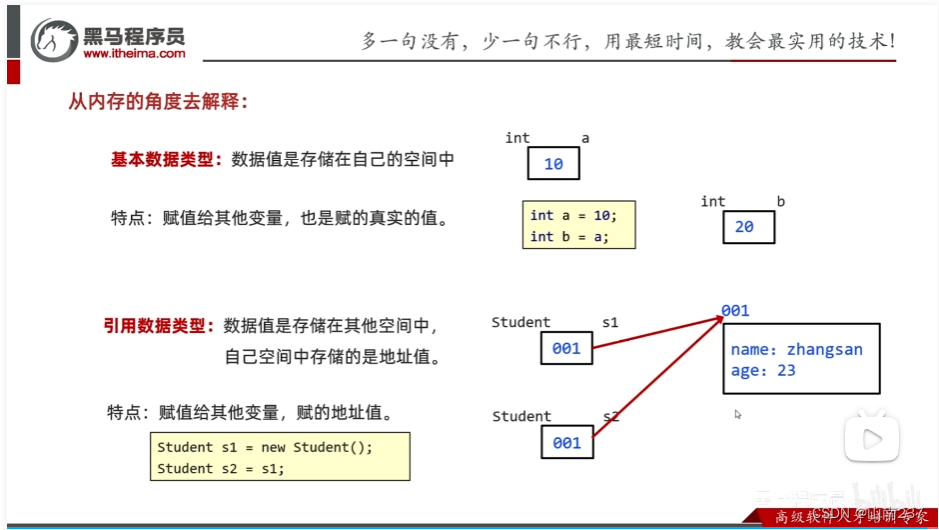
【Android学习专题】java基本语法和概念(学习记录)
学习记录来自菜鸟教程 Java 变量 Java 中主要有如下几种类型的变量 局部变量 在方法、构造方法或者语句块中定义的变量被称为局部变量。变量声明和初始化都是在方法中,方法结束后,变量就会自动销毁类变量(静态变量) 类变量也声…...
Android系统启动全流程分析
当我们买了一个手机或者平板,按下电源键的那一刻,到进入Launcher,选择我们想要使用的某个App进入,这个过程中,系统到底在做了什么事,伙伴们有仔细的研究过吗?可能对于Framework这块晦涩难懂的专…...
RabbitMQ --- 惰性队列、MQ集群
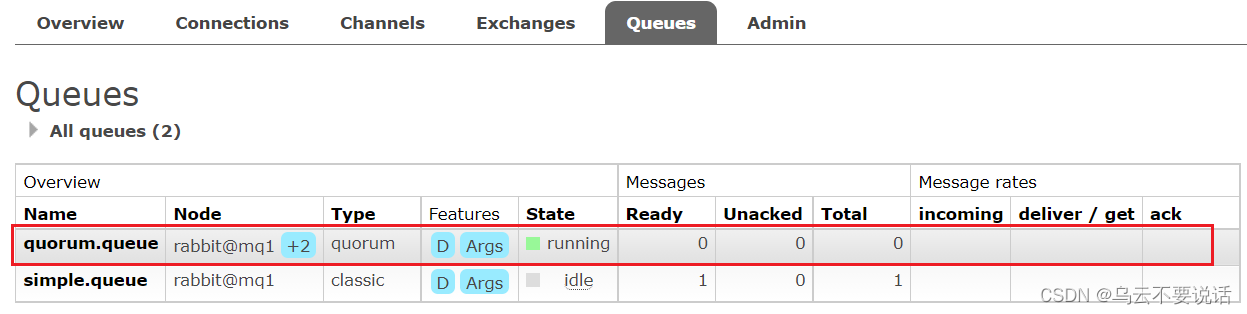
一、惰性队列 1.1、消息堆积问题 当生产者发送消息的速度超过了消费者处理消息的速度,就会导致队列中的消息堆积,直到队列存储消息达到上限。之后发送的消息就会成为死信,可能会被丢弃,这就是消息堆积问题。 解决消息堆积有三种…...

1.Buffer_Overflow-1.Basic_Jump
github上面的练习题 git clone https://github.com/Adamkadaban/LearnPwn 然后开始做 先进行 readelf 然后进行执行看看 是怎么回事 ./buf1发现就是一个输入和输出 我们checksec看看 发现stack 保护关闭 开启了NX保护 我们进入ida64看看反汇编 我习惯先看看字符串 SHITF…...

MySQL入门语法第三课:表结构的创建
数据表结构 定点数类型decimal(m,d) m表示数字总位数 d表示小数位数 ★创建数据表先要选择数据库 1 . CREATE TABLE 表名称 创建数据表 (字段名1 数据类型1 [,字段名2 数据名2] [, .....] ); 一个字段写一行 修改表名 alter table 旧表名 rename 新表名…...
SpringSecurity框架学习与使用
SpringSecurity框架学习与使用 SpringSecurity学习SpringSecurity入门SpringSecurity深入认证授权自定义授权失败页面权限注解SecuredPreAuthorizePostAuthorizePostFilterPreFilter 参考 SpringSecurity学习 SpringSecurity入门 引入相关的依赖,SpringBoot的版本…...
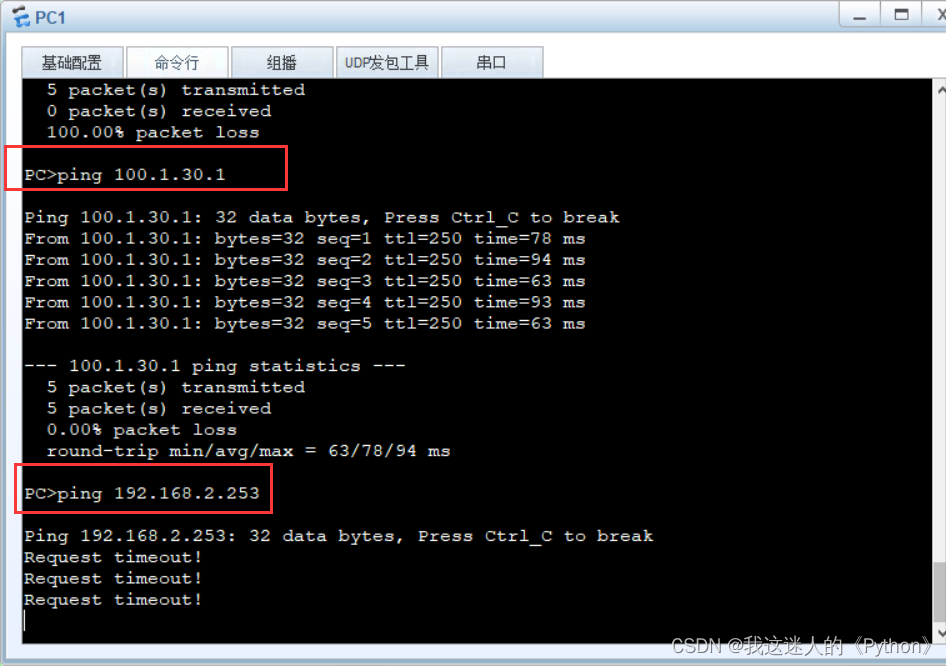
DHCP+链路聚合+NAT+ACL小型实验
实验要求: 1.按照拓扑图上标识规划网络。 2.使用0SPF协议进程100实现ISP互通。 3.私网内PC属于VLAN1O, FTP Server属于VLAN2O,网关分 别为所连接的接入交换机,其中PC要求通过DHCP动态获取 4:私网内部所有交换机都为三层交换机,请合理规划VLAN&#…...
西瓜书读书笔记整理(三)—— 第二章 模型评估与选择
第二章 模型评估与选择 第 2 章 模型评估与选择2.1 经验误差与过拟合1. 错误率 / 精度 / 误差2. 训练误差 / 经验误差 / 泛化误差3. 过拟合 / 欠拟合4. 学习能力5. 模型选择 2.2 评估方法1. 评估方法概述2. 留出法3. 交叉验证法4. 自助法5. 调参 / 最终模型 2.3 性能度量1. 回归…...

AcWing算法提高课-1.3.6货币系统
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 本题链接(AcWing) 点这里 题目描述 给你一个n种面值的货币系统,求组成面值为m的货币有多少种方案。 输入格式 第一行,包含两个整数n和m。 接…...

vue3回到上一个路由页面
学习链接 Vue Router获取当前页面由哪个路由跳转 在Vue3的setup中如何使用this beforeRouteEnter 在这个路由方法中不能访问到组件实例this,但是可以使用next里面的vm访问到组件实例,并通过vm.$data获取组件实例上的data数据getCurrentInstance 是vue3提…...

Linux三种网络模式 | 仅主机、桥接、NAT
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Linux三种网络模式 仅主机模式:虚拟机只能访问物理机,不能上网 桥接模式:虚拟机和物理机连接同一网络,虚拟机和物理机…...

数据库设计与前端框架
数据库设计与前端框架 学习目标: 理解多租户的数据库设计方案 熟练使用PowerDesigner构建数据库模型理解前端工程的基本架构和执行流程 完成前端工程企业模块开发 多租户SaaS平台的数据库方案 多租户是什么 多租户技术(Multi-TenancyTechnology&a…...

技术探秘:揭秘Bean Factory与FactoryBean的区别!
大家好,我是小米,一个热衷于技术分享的29岁小编。今天,我们来聊一聊在Spring框架中常用的两个概念:beanFactory和FactoryBean。它们虽然看似相似,但实际上有着不同的用途和作用。让我们一起来揭开它们的神秘面纱吧&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
