VP记录:Educational Codeforces Round 148 (Rated for Div. 2) A~D1
传送门:CF
前题提要:本人临近期中,时间较紧,且关于D2暂时没有想到优化算法,因此准备留着以后有时间再继续解决
A题:A. New Palindrome
简单的模拟题,考虑记录每一个字母出现的次数.很容易发现奇数次的数字只能出现一次.因为最多只能在正中间放一个.并且因为不能和初始字符相同,因此我们出现此处大于等于2的字符至少应该出现两个(这样可以保证交换).
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {int T=read();while(T--) {map<char,int>mp;string s;cin>>s;for(int i=0;i<s.length();i++) mp[s[i]]++;int cnt1=0,cnt2=0;int sum=0;for(auto it : mp) {if(it.second&1) {cnt1++;sum+=it.second;}else cnt2++;}if(cnt1>1) cout<<"NO"<<endl;else {if((cnt2==1&&sum<=1)||cnt2==0) cout<<"NO"<<endl;else cout<<"YES"<<endl;}}return 0;
}
B题:Maximum Sum
不难发现我们只有两种操作,并且有一个很重要的性质就是两个操作的操作次数总和必须等于 K K K.所以我们不妨枚举第一种操作的操作次数.这样的话,我们就知道两种操作分别操作了多少次了.我们还发现 2 ∗ k < n 2*k<n 2∗k<n,这就保证了我们删除数字的时候是不会发生交叉的.
考虑将数组进行一个排序.然后枚举两种操作的次数,对于所有情况取一个 m a x max max即可.
作为B题,本题思维难度较低
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];int Sum[maxn];
signed main() {int T=read();while(T--) {int n=read();int k=read();int sum=0;for(int i=1;i<=n;i++) {a[i]=read();sum+=a[i];}sort(a+1,a+n+1);for(int i=1;i<=n;i++) Sum[i]=Sum[i-1]+a[i];int maxx=-ll_INF;for(int i=0;i<=k;i++) {int num=k-i;maxx=max(maxx,sum-(Sum[i*2])-(Sum[n]-Sum[n-num]));}cout<<maxx<<endl;}return 0;
}
C题:C. Contrast Value
一道简单思维题.发现我们需要构造一个序列满足相邻差的和与原序列一样.
因为是子序列,我们不妨考虑在原序列中进行删数,这样最终留下来的数字就是原来的序列的子序列了.
因为要满足相邻差不变.所以我们想一下什么情况下删除一个数会不改变相邻的差的总和呢.诶,我们随便试一试就会发现应该是一个单调序列除首尾以外的中间数字.这个看起来十分显然并且也不难证明,所以此处就不在提供证明了.
当你想到这一点之后本题也就不难解决了.只要考虑保留一段单调序列的首尾数字即可.
但是有一个小细节需要注意,也就是当我们相邻的两个数相等时,此时既可以看成单调增序列,也可以看成单调减序列,此时需要单独考虑,这样可以避免影响之后的单调性判断
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];
int main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) {a[i]=read();}if(n==1) {cout<<1<<endl;continue;}if(n==2) {//两个数的时候是需要特判断的,因为这两个数可能相等也可能不同.if(a[2]==a[1]) {cout<<1<<endl;continue;}else {cout<<2<<endl;continue;}}int flag=a[2]>=a[1]?1:-1;if(a[2]==a[1]) flag=0;vector<int>ans;ans.push_back(a[1]);for(int i=3;i<=n;i++) {if(flag==1) {if(a[i]>=a[i-1]) continue;else {ans.push_back(a[i-1]);flag=-1;}}else if(flag==-1){if(a[i]>a[i-1]) {ans.push_back(a[i-1]);flag=1;}else continue;}else {if(a[i]>a[i-1]) flag=1;else if(a[i]<a[i-1]) flag=-1;else flag=0;}}cout<<ans.size()+(a[n]==ans.back()?0:1)<<endl;//注意最后的一个数字肯定是属于一段序列的尾部!!!}return 0;
}
D1:Red-Blue Operations (Easy Version)
首先读完题目不难发现有一个贪心想法:那就是尽量的让这个数组中的最小的那一个数字增加(此处的最小是指每一次操作后的最小).
所以不妨先对原数组进行一个排序.
诶,然后我们把玩一下题意,会发现一个简单的小结论.对于任意一位上的数字来说,这个数字最大的增加幅度只可能是最后一次操作.因为对于这个数字来说,我们每一次都是先增后减.并且减的肯定比增的要多.所以此时增加幅度要么是第一次对该数字进行的操作,要么是经过加减循环之后最后一次的加的操作.我们发现如果是后者的话,显然不如直接加最后一次操作来的更为优秀.诶,所以此时我们就有了一个结论,对于一个位置上的数字来说,我们想要最大化的增加他,就加一个最大的数字即可
然后对于本题,我们考虑使用二分答案,先来简单的证明一下二分的单调性.
我们二分最终的符合的数字 m i d mid mid.我们先来想一下对于一个数列来说,如何才是最佳的改变方法.利用之前叙述的小结论.我们贪心的去想,对于小于 m i d mid mid的所有数字,我们都给它加上最大的操作,此时这个数字变的肯定是最大的.那么假设我们操作完所有小于 m i d mid mid的数字,此时我们肯定是剩下来一些操作没有完成(当然也可能没有,此处分析有剩下来的情况).因为我们想要使用之前的小结论,此时我们就需要保证剩下来的所有操作都是在上边的最大操作之前完成的.
我们此时有几种情况能解决剩下来的操作:
1.我们考虑将剩下来的操作给大于 m i d mid mid的数字,我们发现对于任意的一个大于 m i d mid mid的数字,我们可以每一次承担2次操作然后换来一次减一(至于为什么是连续的两次操作,证明并不难,因为篇幅原因请自行理解)
2.我们考虑将剩下来的操作给之前小于mid但是现在大于mid的数字,我们发现对于那些数字,我们也可以承担2次操作然后换来一次减一
3.我们先进行上述的两种必然可行的方案.假设我们此时还剩下一些操作.那么我们再进行第三种操作.此时我们的情况是所有数组中的数字都是不能再承担两次操作了.那么此时我们会发现对于大于 m i d mid mid的数字来说,我们可以花费奇数次操作来发生正贡献(加减加,依旧是加).并且不单单是这一点,只要我们有两个大于mid的数字,对于任意奇偶的需要操作数,我们都可以完成.因为对于偶数,我们可以拆成两个奇数
4.还需要注意的是,当所有的数列中的数字都大于当前的 m i d mid mid时,此时我们需要特判,因为此时只要我们有两个数,那么我们就可以采取第三种方案来满足题意.如果只有一个数,我们需要判断操作数的奇偶性
基于上述的几种改变方法,我们此时来考虑二分的单调性.
1.假设当前的 m i d mid mid满足题意,为什么不需要考虑小于 m i d mid mid?
显然当前的 m i d mid mid满足题意,我们只需要考虑大于 m i d mid mid的答案是否存在即可,因为我们最终是取 m a x max max的
2.假设当前的 m i d mid mid不满足题意,为什么不需要考虑大于 m i d mid mid
我们发现当前 m i d mid mid不满足题意,这意味的当前我们无法分配操作数.假设我们此时遇到了一个更大的 m i d 2 mid2 mid2,设原本的分界点为 p o s pos pos(也就是 a [ p o s ] a[pos] a[pos]恰好大于等于mid).我们此时需要将 a [ p o s ] a[pos] a[pos]也变得大于 m i d 2 mid2 mid2.但是试想一下,我们之前已经无法做到保证所有的数字大于 m i d mid mid的了.根据贪心的想法,最后的操作必然是加减加的最后一次加.那么之前这样都不满足题意,此时我们需要拿几次"减加"的操作来放到 a [ p o s ] a[pos] a[pos]上,这必然会导致其他位置的数字减少,就更加不能满足题意了.
可能讲的有点抽象,建议结合代码理解一下QAQ,本题虽讲解篇幅较长,但是作为D1,其思维难度并不高
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];int n,q;
int check(int mid,int k) {int temp=k;int pos=n+1;vector<int>b;b.push_back(0);for(int i=1;i<=n;i++) b.push_back(a[i]);//因为a数组加了之后会改变单调性,所以b数组用来重新排序for(int i=1;i<=n;i++) {if(b[i]<mid) {//给每一个小于mid的数字加上当前可行的最大的操作if(b[i]+temp<mid) return false;b[i]+=temp;temp--;} else {pos=i;break;}}int cnt=0;for(int i=pos;i<=n;i++) {//先进行操作1cnt+=b[i]-mid;}temp-=cnt*2;if(temp<=0) return true; if(pos==1) {if(temp&1) return true;else {if(n>=2) return true;else return false;}}sort(b.begin()+1,b.begin()+pos-1);for(int i=pos-1;i>=1;i--) {//再进行操作2int num=(b[i]-mid)*2;if(num<=0) continue;if(temp<=num) {if(temp&1) {temp=1;break;}else {temp=0;break;}}else {temp-=(b[i]-mid)*2;}}if(pos<=n) {//考虑操作3if((n-pos+1)!=1) return true;else if(temp&1) return true;}if(temp>0) return false;else return true;
}
signed main() {n=read(),q=read();for(int i=1;i<=n;i++) {a[i]=read();}sort(a+1,a+n+1);for(int i=1;i<=q;i++) {int k=read();int l=-1e10,r=1e10;int ans=0;while(l<=r) {int mid=(l+r)/2;if(check(mid,k)) {l=mid+1;ans=mid;}else {r=mid-1;}}cout<<ans<<" ";}return 0;
}
相关文章:
 A~D1)
VP记录:Educational Codeforces Round 148 (Rated for Div. 2) A~D1
传送门:CF 前题提要:本人临近期中,时间较紧,且关于D2暂时没有想到优化算法,因此准备留着以后有时间再继续解决 A题:A. New Palindrome 简单的模拟题,考虑记录每一个字母出现的次数.很容易发现奇数次的数字只能出现一次.因为最多只能在正中间放一个.并且因为不能和初始字符相…...
无线模块|如何选择天线和设计天线电路
无线模块的通信距离是一项重要指标,如何把有效通信距离最大化一直是大家疑惑的问题。本文根据调试经验及对天线的选择与使用方法做了一些说明,希望对工程师快速调试通信距离有所帮助。 一、天线的种类 随着技术的进步,为了节省研发周期&…...

(11)LCD1602液晶显示屏
LCD1602(Liquid Crystal Display)液晶显示屏是一种字符型液晶显示模块,可以显示ASCII码的标准字符和其它的一些内置特殊字符,还可以有8个自定义字符,自带芯片扫描 显示容量:162个字符,每个字符…...

类和对象下
文章目录 一、初始化列表1、语法:2、初始化顺序 二、static成员三、友元1、友元函数2、友元类 四、拷贝对象时的编译器优化例1、例2、例3、 一、初始化列表 1、语法: 初始化列表: 以一个冒号开始,接着是一个以逗号分隔的数据成员…...
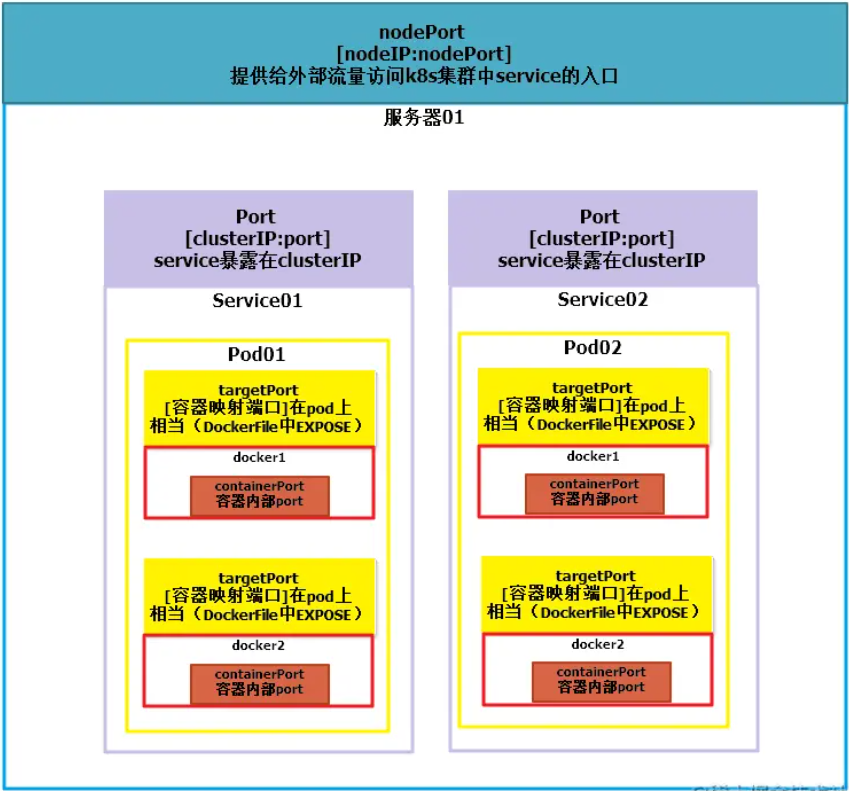
【云计算•云原生】4.云原生之什么是Kubernetes
文章目录 Kubernetes概念Kubernetes核心概念集群podConfigMap Kubernetes架构master节点的组件worker节点组件 Kubernetes网络架构内部网络外部网络 k8s各端口含义 Kubernetes概念 K8S就是Kubernetes,Kubernetes首字母为K,末尾为s,中间一共有…...

云厂商降价潮背后:来中小企业战场「拼刺刀」
如果说过往云厂商的降价打响的是从C端进军B端的营销战,那么在这一轮降价潮背后,对应的则是云厂商从大型KA客户向中小企业进军的信号,强被集成,强获客。 云厂商又一轮降价潮袭来。 5月16日,移动云宣布部分产品线最高降…...

2-单片机GPIO相关知识点及流水灯和按键采集小实验
目录 小问题 :单片机上电后第一个执行的程序是? 【1】GPIO 1.定义 2.应用 I - Input 输入采集 O - Output 输出控制 3.GPIO结构框图 4.功能描述 输入功能 5.相关寄存器 【2】输出控制实验 实验:点亮一盏LED灯 1.实验…...

基础知识(王爽老师书第一章)
文章目录 基础知识1.1 引言1.2 机器语言1.2 引言汇编语言的产生1.3 汇编语言的组成1.4 存储器1.5 指令和数据1.6 存储单元1.7 CPU对存储器的读写1.8 地址总线1.9 数据总线1.10 控制总线小结检测点1.11.11 内存地址空间1.12 主板1.13 接口卡1.14 各类存储器芯片1.15 内存地址空间…...

非煤矿山电子封条建设算法 yolov8
非煤矿山电子封条建设算法模型通过yolov8网络模型AI视频智能分析技术,算法模型对作业状态以及出井入井人员数量变化、人员睡岗离岗等情况实时监测分析,及时发现异常动态,自动推送生成的违规截图报警信息。现代目标检测器大部分都会在正负样本…...

七大软件架构设计原则详解
目录 1、概述 2、七大设计原则 2.1、开闭原则 2.2、里氏替换原则 2.3、依赖倒置原则 2.4、单一职责原则 2.5、接口隔离原则 2.6、迪米特法则 2.7、合成复用原则 3、最后 VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...&…...
【Python入门】Python循环语句(while循环的嵌套应用)
前言 📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于Python零基础入门系列,本专栏主要内容为Python基础语法、判断、循环语句、函…...

数据来源和搜集
数据搜集 文章目录 数据搜集1 数据来源1.1 数据的间接来源1.2 间接数据的评价1.3 数据的直接来源 2 调查数据2.1概率抽样2.2 非概率抽样2.3 概率抽样 *vs.*非概率抽样 3 搜集数据的方法4 实验数据4.1 实验组与对照组4.2 实验中的若干问题 1 数据来源 所有统计数据都来源于社会…...
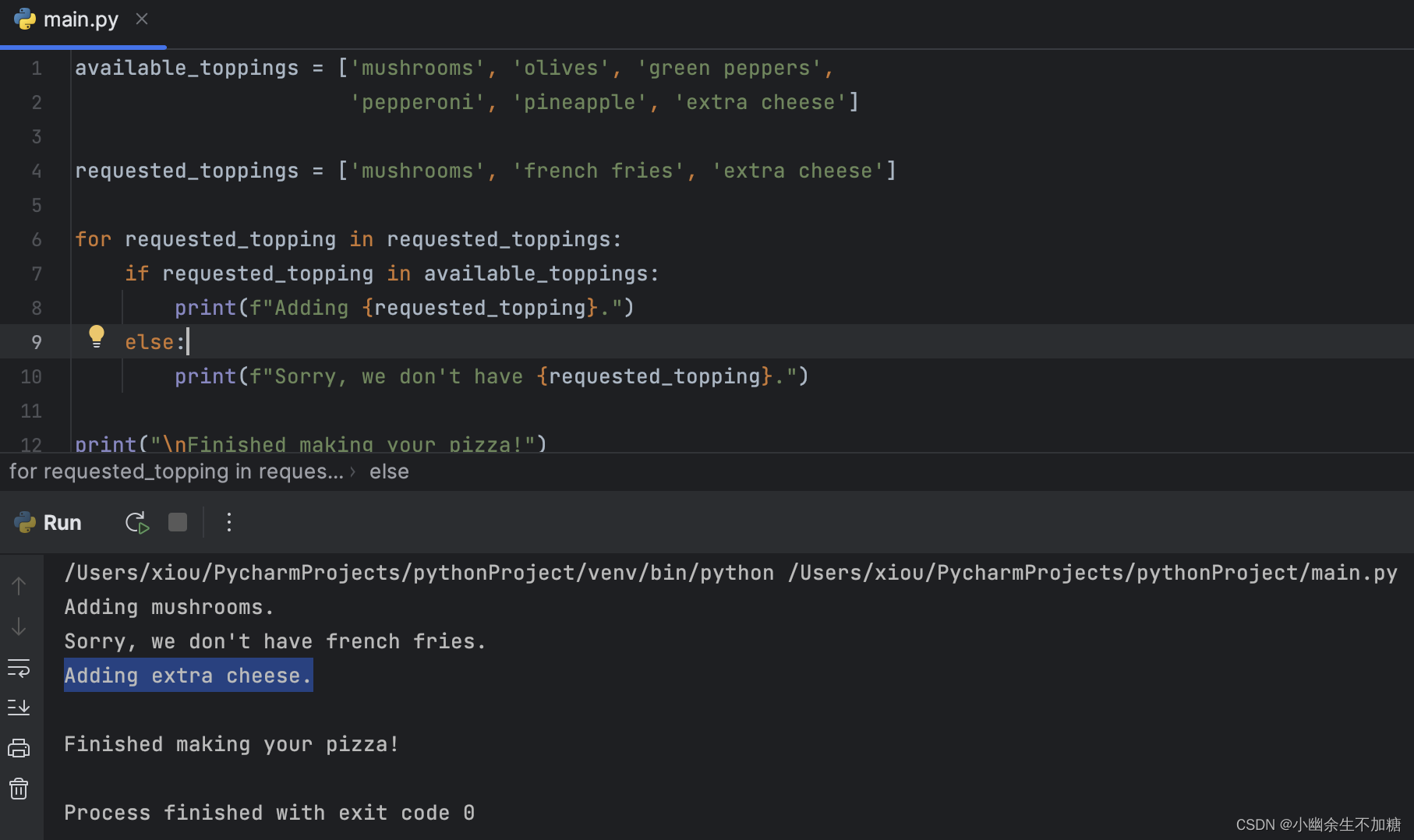
Python入门(七)if语句(二)
if语句(二) 1.if语句1.1 简单的if语句1.2 if-else语句1.3 if-elif-else结构1.4 使用多个elif代码块1.5 使用多个elif代码块 2.使用if语句处理列表2.1 检查特殊元素2.2 确定列表不是空的2.3 使用多个列表 作者:xiou 1.if语句 前面我们理解了…...

[元带你学: eMMC完全解读 2] eMMC协议相关术语与定义
声明 主页:元存储的博客_CSDN博客 依公开知识及经验整理,如有误请留言。 个人辛苦整理,付费内容,禁止转载。 所在专栏 《元带你学: eMMC完全解读》 内容摘要 前言 文中列出了常用和不常用的eMMC 术语, 只需要了解常用术语就完全够用, 非常用术语几乎都用不上,只要遇到的…...

预测杭州五一黄金周的旅游出行人数
对于杭州五一黄金周的旅游出行人数的预测,可以从以下几个方面进行考虑。 一、历史数据的分析 杭州作为一个旅游胜地,每年的五一黄金周都吸引了大量的游客前来游玩。历史数据可以为我们提供有用的信息,帮助我们预测今年的旅游出行人数。 1.…...

内防泄密重要,还是外防窃密重要?
内防泄密是组织为防止内部敏感信息未经授权泄露所采取的各种管理与技术措施的总称。它主要针对内部人员的信息访问与操作行为进行管控,减少故意或疏忽泄密事件的发生几率。 内防泄密的工作,通常包括员工管理、权限管控、监控检查、分级保护、离岗管控、技术防护、事…...

ChatGPT:2. 使用OpenAI创建自己的AI网站:1. 初探API
使用OpenAI创建自己的AI网站 如果你还是一个OpenAI的小白,有OpenAI的账号,但想调用OpenAI的API搞一些有意思的事,那么这一系列的教程将仔细的为你讲解如何使用OpenAI的API制作属于自己的AI网站。博主只能利用下班时间更新,进度慢…...

5月17日,今日信息差
1、中老铁路运输货物突破2000万吨。其中,跨境货运量超400万吨,货值达177亿元 2、北京首个5.5G实验基站在昌平区的国际信息港建设开通,5.5G将在速率、时延、连接规模和能耗方面全面超越现有5G,实现下行万兆和上行千兆的峰值速率…...
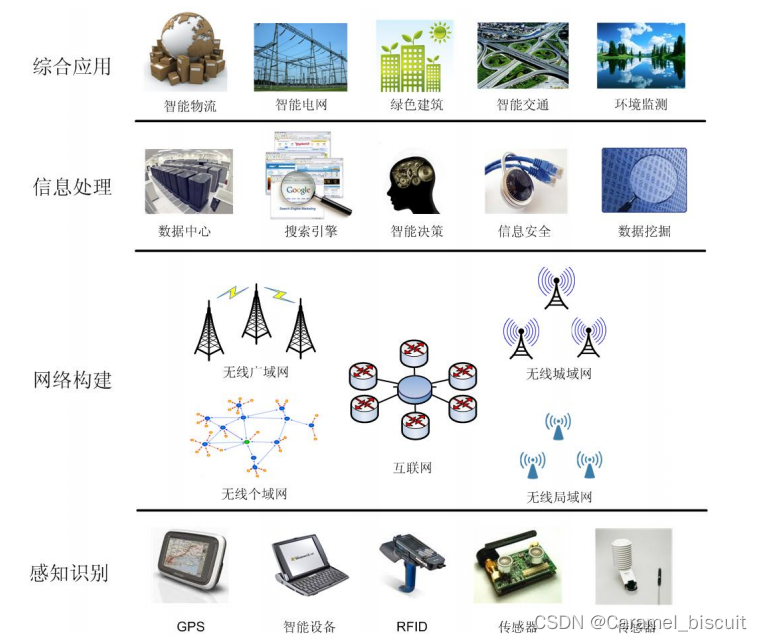
物联网的体系架构
物联网中常见的计算模式:云计算、边缘计算、雾计算等 云计算:一种利用互联网实现随时随地、按需、便捷地使用共享计算设施、存储设备、应用程序等资源的计算模式。边缘计算:在靠近物或数据源头的网络边缘侧,融合网络、计算、存储…...

Golang交叉编译
Golang交叉编译遇到的问题 交叉编译go支持的平台和版本 交叉编译 go支持的平台和版本 查询命令: go tool dist list显示结果: aix/ppc64android/386android/amd64android/armandroid/arm64darwin/amd64darwin/arm64dragonfly/amd64freebsd/386freebsd/…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
