云厂商降价潮背后:来中小企业战场「拼刺刀」

如果说过往云厂商的降价打响的是从C端进军B端的营销战,那么在这一轮降价潮背后,对应的则是云厂商从大型KA客户向中小企业进军的信号,强被集成,强获客。
云厂商又一轮降价潮袭来。
5月16日,移动云宣布部分产品线最高降幅达60%,降价政策将于 5 月 17 日正式生效。与移动云一同推出降价通知的还有腾讯云,部分产品线最高降幅达 40%,降价政策将在 6 月 1 日正式生效。此外,在上个月,阿里云也曾发动“史上最大规模降价”,继4月降价之后,核心产品价格再次全线下调至50%。
实际上,这并不是云厂商第一次迎来降价潮,其降价幅度也并非最大,产品覆盖度也并非最全,但这种动作仍然值得回味。在经济复苏向好,企业IT预算逐步回春的当下,云厂商这次降价背后,传递出的信号是什么?
如今,国内云市场大型企业数量少,且获客普遍偏难,同时伴随着过去两年运营商云的崛起,在金融、政务等大型客户层面,云厂商的竞争愈发激烈且近乎红海。
但就业务而言,增长故事却仍需要新的支点。如果说过往云厂商的降价打响的是从C端进军B端的战斗,那么在这一轮降价潮背后,对应的则是云厂商从大型KA客户向中小企业进军的信号,驶向TOB纵深。
但同时,这也预示着,云计算正在进入新的洗牌期。
一、新一轮降价潮来了
从互联网云到运营商云,枪声被一一打响。
这次降价潮中,不同于以往多以互联网云厂商掀起的降价潮,此次降价潮中移动云的身影引起了业内人士的广泛关注。
具体来看,移动云此次降价产品涉及云主机、云安全中心、云硬盘。其中通用入门型云主机、通用网络优化型云主机均降价 60%,分别降至包年 240 元、806.4 元;云安全中心降价 50% 至包年 360 元;云硬盘备份降价 50% 至包年 7.2 元。

腾讯云涉及的产品则在云网络、数据库、云安全方面。其中,腾讯云对负载均衡CLB的LCU费降价18%,对标准型NAT网关降价15%;数据库TDSQL-Cserverless对比同规格包年包月产品降幅高达25%,Serverless按实际使用量计费的特性可帮助用户最高降本80%;腾讯云主机安全基础版将对全网中小企业免费开放。
而阿里云此前降价的产品中,弹性计算7代实例和倚天实例降价最高20%,存储OSS深度冷归档相比此前最低档价格低50%,网络负载均衡SLB和NAT网关降价15%,数据库RDS倚天版降价最高40%,视频云和CDN降价最高20%,安全Web应用防火墙降价最高30%。

总体来看,移动云涉及产品更多是底层硬件,通俗来讲就是机房中的存储、服务器等出租价格的降低。互联网云厂商降价产品则主要涉及数据库等公有云的基础能力。
值得注意的是,此次涉及的产品范围更多集中在PaaS层,且比起之前云厂商产品降低的价格,此次幅度更大。
以阿里云为例,其第一轮降价要追溯到2014年,降价产品主要为云服务器和云数据库产品,价格下调达到20%。再有就是2016年关于全线云产品价格的下调,以及2018年对弹性计算、存储、性能测试PTS在内的核心产品的降价。
除了阿里云,腾讯云、华为云、京东云等在最近几年,都相继在产品价格上都采取了相对应的调整。也曾引起过规模不大的云计算降价潮。但总体来看,引领者、参与者都是互联网云厂商以及国外的云巨头。
且在过去,以国外云巨头引领的降价潮,国内参与者主要是互联网云厂商和专业云厂商,底层逻辑更多是对国外云巨头抢占国内市场的防御动作;以国内互联网云厂商引领的降价潮,主要参与者是云厂商自身,底层逻辑大部分是从C端到B端的动作信号和营销手段。
但这次由于运营商云的参与,也意味着,这轮降价潮对应的是真正企业客户层面的“拼刺刀”。
二、从KA客户到中小企业,打响第一枪
云厂商集体减速,已经是整个云计算领域需要共同面对的命题。
一组数据显示,阿里云在2022财年首次实现全年盈利,成为中国唯一一家实现盈亏平衡的云服务厂商,但也难掩收入增速放缓的现状。不仅2022财年的4个季度,阿里云的增速分别为30%、33%、20%、12%,到2023财年Q3,这一数字已降到3%。
这是整个互联网云厂商的缩影。反观“国家队”运营商云,过去2年其进击节奏明显加快。
公开数据显示,2022年中国电信天翼云收入为579亿人民币,同比增长108%。2022年中国移动云收入达到503亿人民币,增速为108.1%。
尽管增速不同,但对两者而言其未来的目标都较为一致。即伴随着金融、政务客户的账“被瓜分”,对运营商云而言,其需要寻找到下一个增长点;而对互联网云厂商而言,也需要基于过往互联网侧的优势,拿下这些需要真正拼刺刀的新阵地。
以金融领域为例,大型银行已经成为存量市场,未来随着数字化的逐渐渗透,这些大型政企的客户资源被“消耗殆尽”之后,运营商云又该从哪里寻找增量?答案是城商行。
“基本上过去两年各个大行的核心系统都已经完成国产替代了,接下来需要我们把这些功能标准化,拿下更多的城商行客户。”一位云厂商数据库负责人告诉我们。
同样的现象更出现在更多领域。即在屈指可数的大企业之外,云厂商的眼光正在撒向包括工业、能源、建筑等诸多其它民生行业。
这也是这次降价潮各家想对外以及对渠道商和集成商传递的声音所在。
即无论是运营商云,还是互联网云想要触达大型企业的边缘业务以及中小企业,都需要借力打力。而较低的价格,可以让渠道商的成本降低,更利于被集成。
正如阿里云PaaS层应用降价,将使得一些ISV和渠道商的利润率显著提高。一方面合作伙伴可以有更大的空间来操作,选择与阿里云集成,另一方面其也能为中小企业提供更低的价格。在中小企业不断渗透后,也将提高阿里云的用云量,提高阿里云的营收。实现整个链条营收增长闭环,有助于打造增长飞轮。
三、云厂商的新洗牌期
在中国,企业标准化程度低,在部署数字化软件时,定制化要求较高。为了满足企业的个性化需求,软件厂商往往将产品做的大而全,以此尽可能满足企业各种“变态”需求。
例如,大部分企业都采用混合云、多云部署,这就要求数据、服务、业务在云间的穿透能力增强,能够统一提供部署所需的元素,包括服务器、网络、存储、数据库、操作系统等,在不同的系统和云之间协调,更集成的大而全平台更易被采纳。
这使得云厂商本来应该专注底层能力的竞争,转到了软件具体应用的竞争。而有的厂商则从原本专注具体应用竞争转到底层能力竞争。
然而,这种“大而全”的中国特色背后,使得诸多中腰部的创新云厂商开始放弃自身核心业务的研发,更多的成为“卖服务器”的企业,由此带来的是企业之间的价格战、内卷。
但这个降价潮是一个新契机。
随着头部云厂商相关业务的降价,将压缩中腰部云厂商相对应部分业务的生存空间。例如移动云在主机、云存储硬件的降价,阿里云、腾讯云在数据库等领域降价,相对应的其他中腰部云厂商或选择降价,或放弃底层业务。倒逼企业往转向更专、精的领域,如数据库、存储、计算、中间件等PaaS层业务。
“尽管国内目前和接下来几年仍然会以私有化部署为主导,但终局一定只能几大云厂商提供底层算力资源。”一位投资人告诉我们,“剩余的空间都在PaaS和SaaS,或者是MaaS,这会是未来IT行业的主要形态。”
能明显预测到的是,伴随着这波云计算领域的降价潮,国内云厂商头部效应将愈发明显,云市场的变化和新规则也将缓慢成型,“这波降价潮的后续影响将会贯穿整个2023年。”
相关文章:

云厂商降价潮背后:来中小企业战场「拼刺刀」
如果说过往云厂商的降价打响的是从C端进军B端的营销战,那么在这一轮降价潮背后,对应的则是云厂商从大型KA客户向中小企业进军的信号,强被集成,强获客。 云厂商又一轮降价潮袭来。 5月16日,移动云宣布部分产品线最高降…...

2-单片机GPIO相关知识点及流水灯和按键采集小实验
目录 小问题 :单片机上电后第一个执行的程序是? 【1】GPIO 1.定义 2.应用 I - Input 输入采集 O - Output 输出控制 3.GPIO结构框图 4.功能描述 输入功能 5.相关寄存器 【2】输出控制实验 实验:点亮一盏LED灯 1.实验…...

基础知识(王爽老师书第一章)
文章目录 基础知识1.1 引言1.2 机器语言1.2 引言汇编语言的产生1.3 汇编语言的组成1.4 存储器1.5 指令和数据1.6 存储单元1.7 CPU对存储器的读写1.8 地址总线1.9 数据总线1.10 控制总线小结检测点1.11.11 内存地址空间1.12 主板1.13 接口卡1.14 各类存储器芯片1.15 内存地址空间…...

非煤矿山电子封条建设算法 yolov8
非煤矿山电子封条建设算法模型通过yolov8网络模型AI视频智能分析技术,算法模型对作业状态以及出井入井人员数量变化、人员睡岗离岗等情况实时监测分析,及时发现异常动态,自动推送生成的违规截图报警信息。现代目标检测器大部分都会在正负样本…...

七大软件架构设计原则详解
目录 1、概述 2、七大设计原则 2.1、开闭原则 2.2、里氏替换原则 2.3、依赖倒置原则 2.4、单一职责原则 2.5、接口隔离原则 2.6、迪米特法则 2.7、合成复用原则 3、最后 VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...&…...
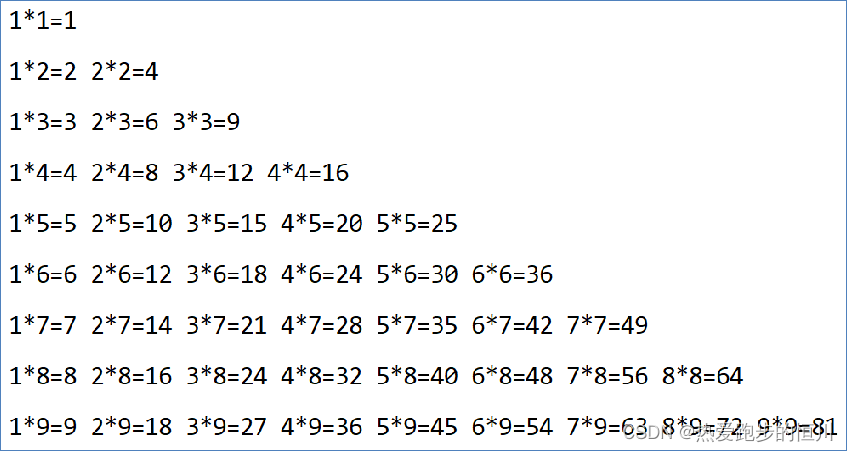
【Python入门】Python循环语句(while循环的嵌套应用)
前言 📕作者简介:热爱跑步的恒川,致力于C/C、Java、Python等多编程语言,热爱跑步,喜爱音乐的一位博主。 📗本文收录于Python零基础入门系列,本专栏主要内容为Python基础语法、判断、循环语句、函…...

数据来源和搜集
数据搜集 文章目录 数据搜集1 数据来源1.1 数据的间接来源1.2 间接数据的评价1.3 数据的直接来源 2 调查数据2.1概率抽样2.2 非概率抽样2.3 概率抽样 *vs.*非概率抽样 3 搜集数据的方法4 实验数据4.1 实验组与对照组4.2 实验中的若干问题 1 数据来源 所有统计数据都来源于社会…...
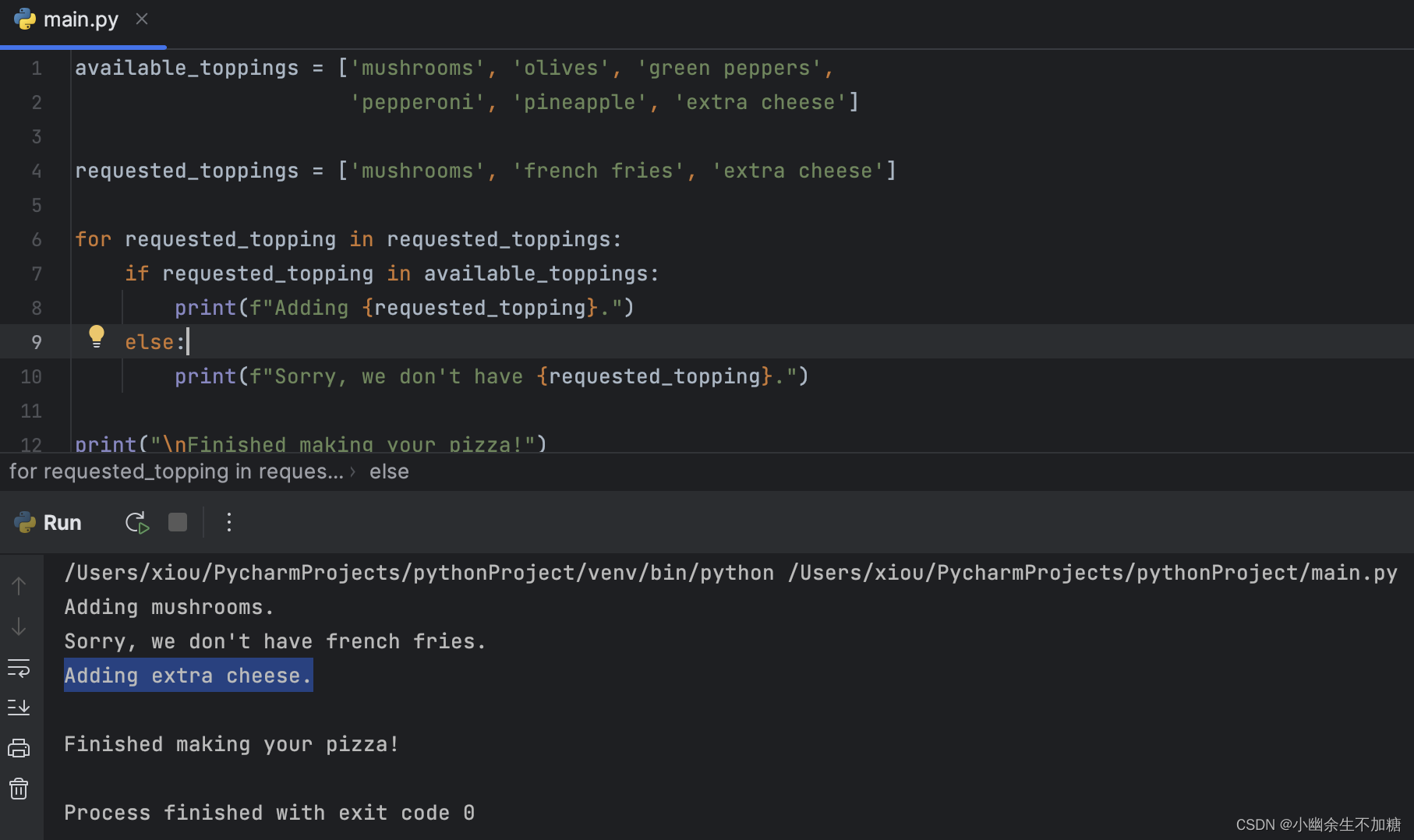
Python入门(七)if语句(二)
if语句(二) 1.if语句1.1 简单的if语句1.2 if-else语句1.3 if-elif-else结构1.4 使用多个elif代码块1.5 使用多个elif代码块 2.使用if语句处理列表2.1 检查特殊元素2.2 确定列表不是空的2.3 使用多个列表 作者:xiou 1.if语句 前面我们理解了…...

[元带你学: eMMC完全解读 2] eMMC协议相关术语与定义
声明 主页:元存储的博客_CSDN博客 依公开知识及经验整理,如有误请留言。 个人辛苦整理,付费内容,禁止转载。 所在专栏 《元带你学: eMMC完全解读》 内容摘要 前言 文中列出了常用和不常用的eMMC 术语, 只需要了解常用术语就完全够用, 非常用术语几乎都用不上,只要遇到的…...

预测杭州五一黄金周的旅游出行人数
对于杭州五一黄金周的旅游出行人数的预测,可以从以下几个方面进行考虑。 一、历史数据的分析 杭州作为一个旅游胜地,每年的五一黄金周都吸引了大量的游客前来游玩。历史数据可以为我们提供有用的信息,帮助我们预测今年的旅游出行人数。 1.…...

内防泄密重要,还是外防窃密重要?
内防泄密是组织为防止内部敏感信息未经授权泄露所采取的各种管理与技术措施的总称。它主要针对内部人员的信息访问与操作行为进行管控,减少故意或疏忽泄密事件的发生几率。 内防泄密的工作,通常包括员工管理、权限管控、监控检查、分级保护、离岗管控、技术防护、事…...

ChatGPT:2. 使用OpenAI创建自己的AI网站:1. 初探API
使用OpenAI创建自己的AI网站 如果你还是一个OpenAI的小白,有OpenAI的账号,但想调用OpenAI的API搞一些有意思的事,那么这一系列的教程将仔细的为你讲解如何使用OpenAI的API制作属于自己的AI网站。博主只能利用下班时间更新,进度慢…...

5月17日,今日信息差
1、中老铁路运输货物突破2000万吨。其中,跨境货运量超400万吨,货值达177亿元 2、北京首个5.5G实验基站在昌平区的国际信息港建设开通,5.5G将在速率、时延、连接规模和能耗方面全面超越现有5G,实现下行万兆和上行千兆的峰值速率…...
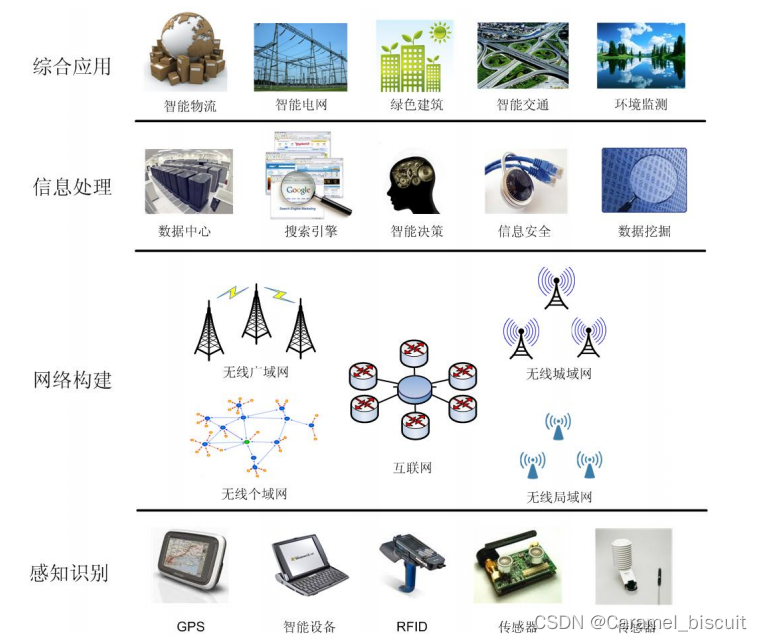
物联网的体系架构
物联网中常见的计算模式:云计算、边缘计算、雾计算等 云计算:一种利用互联网实现随时随地、按需、便捷地使用共享计算设施、存储设备、应用程序等资源的计算模式。边缘计算:在靠近物或数据源头的网络边缘侧,融合网络、计算、存储…...

Golang交叉编译
Golang交叉编译遇到的问题 交叉编译go支持的平台和版本 交叉编译 go支持的平台和版本 查询命令: go tool dist list显示结果: aix/ppc64android/386android/amd64android/armandroid/arm64darwin/amd64darwin/arm64dragonfly/amd64freebsd/386freebsd/…...
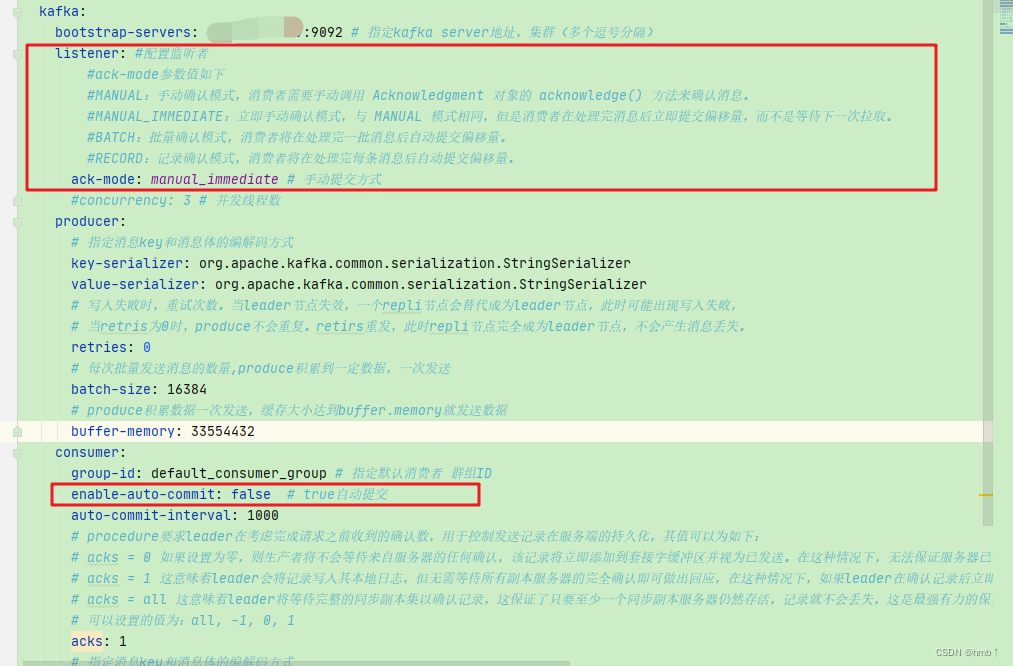
kafka3.x详解
kafka 一、简介1.1、场景选择,与其他mq相比1.2、应用场景1.2.1、流量消峰1.2.2、解耦1.2.3、异步通讯 1.3、消息队列的两种模式1.3.1、点对点模式1.3.2、发布/订阅模式 1.4、Kafka 基础架构 二、安装部署2.1、安装包方式2.2、docker安装方式2.3、docker安装kafka-ma…...

kubectl常用命令|pod生命周期|金丝雀发布|超详细
kubectl常用命令|pod生命周期|金丝雀发布|超详细 一 kubectl常用命令1.1 查看版本信息1.2查看资源对象简写1.3查看集群信息1.4 配置kubectl自动补全1.5node节点查看日志 二 k8s基本信息查看2.1 查看 master 节点状态2.2 查看命令空间2.3 创建和删除命名空间2.4 在命名空间kube-…...

【Linux系统】Linux进程信号详解
Linux进程信号 0 引言1 认识信号1.1 什么是信号1.2 发送信号的本质1.3 信号的处理 2 信号的产生2.1 键盘产生2.2 调用系统函数向进程发送信号2.3 由软件条件产生信号2.4 硬件异常产生信号 3 信号的保存4 信号的处理5 总结 0 引言 本篇文章会从Linux信号的产生到信号的保存&…...

阿里云u1服务器通用算力型CPU处理器性能测评
阿里云服务器u1通用算力型Universal实例高性价比,CPU采用Intel(R) Xeon(R) Platinum,主频是2.5 GHz,云服务器U1实例的基准vCPU算力与5代企业级实例持平,最高vCPU算力与6代企业级实例持平,提供2c-32c规格和1:1/2/4/8丰富…...

hive的详细使用文档和使用案例
目录 Hive 简介安装连接到Hive创建数据库创建表加载数据查询数据修改表删除表 使用案例结论 Hive 简介 Hive是一个基于Hadoop的数据仓库工具,可以将结构化数据映射到Hadoop HDFS上,并提供SQL查询功能。Hive的设计目标是让那些熟悉SQL语言的用户能够在Ha…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
