机器学习之线性回归
往期目录
python在线性规划中的应用
文章目录
- 一、线性回归算法概述
- 1.1 什么是线性回归?
- 1.2 线性回归算法原理
- 1.3 线性回归的应用场景
- 二、线性回归算法Python实现
- 2.1 导入必要的库
- 2.2 随机生成数据集
- 2.3 拟合模型
- 2.4 预测结果
- 2.5 结果可视化
- 三、完整代码
线性回归是机器学习中最基础的算法之一,其原理简单易懂,应用广泛。
回归分析(Regression Analysis)是统计学的数据分析方法,目的在于了解两个或多个变量间是否相关、相关方向与强度,并建立数学模型以便观察特定变量来预测其它变量的变化情况。
线性回归算法(Linear Regression)的建模过程就是使用数据点来寻找最佳拟合线。公式,y = mx + c,其中 y 是因变量,x 是自变量,利用给定的数据集求 m 和 c 的值。
线性回归又分为两种类型,即 简单线性回归(simple linear regression),只有 1 个自变量;*多变量回归(multiple regression),至少两组以上自变量。
一、线性回归算法概述
1.1 什么是线性回归?
线性回归是一种常见的监督学习算法,用于预测一个连续的输出变量(也称为响应变量或因变量)和一个或多个输入变量(也称为自变量)之间的关系。这种关系可以用一条直线的方程来表达。
1.2 线性回归算法原理
线性回归基于最小二乘法,即寻找一条直线最小化观测数据和线之间的平方误差和。该算法的目标是找到一条最佳拟合直线,使得每个观测值与拟合直线之间的距离最小。
线性回归模型的数学表达式如下:
Y = β 0 + β 1 X 1 + β 2 X 2 + … … + β n ∗ X n Y = β_{0} + β_{1}X_{1} + β_{2}X_{2}+ ……+ β_{n}*X_{n} Y=β0+β1X1+β2X2+……+βn∗Xn
其中, Y Y Y 是响应变量, X 1 X_{1} X1, X 2 X_{2} X2,……, X n X_{n} Xn 是自变量, β 0 , β 1 , β 2 , … … , β n β_{0},β_{1},β_{2},……,β_{n} β0,β1,β2,……,βn 是模型的参数。
线性回归算法主要包括两个步骤:
寻找最佳拟合直线的参数 β 0 , β 1 , β 2 , … … , β n β_{0},β_{1},β_{2},……,β_{n} β0,β1,β2,……,βn。
使用模型对新的数据进行预测。
1.3 线性回归的应用场景
线性回归可以用于许多不同的领域,包括金融、经济学、营销、社会科学等。以下是一些可能的应用场景:
通过销售额和广告支出建立销售预测模型
分析股票市场的趋势和波动
将房价与房屋面积、地理位置等因素联系起来
预测医疗保健成本
二、线性回归算法Python实现
为了实现线性回归算法,我们需要将其转化为一个优化问题。我们需要使用机器学习库 scikit-learn 实现这个问题。下面是实现流程:
2.1 导入必要的库
在开始编写代码之前,我们需要导入一些必要的库,包括 pandas、numpy 和 sklearn 等。这些库使得我们可以轻松地进行数据处理、数学运算和模型训练。下面是导入库的代码示例:
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
2.2 随机生成数据集
在进行机器学习算法时,我们需要先准备合适的数据集。在这个例子中,我们使用一个包含房屋面积和价格的数据集。我们可以使用 pandas 库来加载数据集。下面是加载数据集的代码示例:
# 生成随机数据集
np.random.seed(0) # 设置随机种子
X = np.random.rand(100, 1)
y = 2 + 3*X + np.random.randn(100, 1)
在上述代码中,我们使用 Pandas 的 read_csv() 方法从 CSV 文件中读取数据,并将其划分为输入变量(也称为特征)和输出变量。X 是包含所有输入变量的 NumPy 数组,y 是包含所有输出变量的一维 NumPy 数组。
2.3 拟合模型
接下来,我们需要创建一个 LinearRegression 对象并拟合模型。这个对象将用于训练模型和进行预测。下面是拟合模型的代码示例:
# 创建线性回归对象并拟合数据
reg = LinearRegression().fit(X, y)
上述代码中,我们创建了一个 LinearRegression 对象 regressor,并调用其 fit() 方法来拟合模型。这里的 fit() 方法会自动调整模型参数以最小化观测值和拟合直线之间的误差。
2.4 预测结果
有了拟合的模型后,我们就可以使用它来进行预测了。这里我们可以根据输入变量预测输出变量。下面是预测结果的代码示例:
# 预测新数据
X_new = np.array([[0.5]])
y_new = reg.predict(X_new)# 绘制数据散点图和拟合直线(使用 seaborn 库美化)
sns.set(style='whitegrid', font_scale=1.2)
在上述代码中,我们使用训练好的模型 regressor 来预测输出变量 y 的值。这里的 predict() 方法将根据输入变量 X 来返回相应的预测值 y_pred。
2.5 结果可视化
最后,在得到预测结果之后,我们可以将其可视化。这里我们使用 matplotlib 库来绘制散点图和拟合直线。下面是可视化结果的代码示例
plt.scatter(X, y, alpha=0.8, color='#3F7F4C')
plt.plot(X, reg.predict(X), color='#6D8F18', linewidth=2)
plt.grid(False)
plt.xlabel('xlabel',font)
plt.ylabel('ylabel',font)
plt.show()
在上述代码中,我们使用 matplotlib 库将原始数据绘制为散点图。然后,我们使用 predict() 方法计算出预测结果并绘制一条拟合直线。最后,我们添加一些标题和标签来说明图形内容,并使用 show() 方法展示图形。
三、完整代码
import numpy as np
from sklearn.linear_model import LinearRegression
import seaborn as sns
import matplotlib.pyplot as plt# 生成随机数据集
np.random.seed(0) # 设置随机种子
X = np.random.rand(100, 1)
y = 2 + 3*X + np.random.randn(100, 1)fig,ax = plt.subplots(figsize=(8,6),dpi=300)
plt.tick_params(labelsize=20)
labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontname('Times New Roman') for label in labels]
font = {'family': 'Times New Roman','size': 24}
# font_1 = {'family': 'Times New Roman','size': 14}
plt.rcParams["font.family"] = "Times New Roman" #全图字号新罗马字体# 创建线性回归对象并拟合数据
reg = LinearRegression().fit(X, y)# 预测新数据
X_new = np.array([[0.5]])
y_new = reg.predict(X_new)# 绘制数据散点图和拟合直线(使用 seaborn 库美化)
sns.set(style='whitegrid', font_scale=1.2)plt.scatter(X, y, alpha=0.8, color='#3F7F4C')
plt.plot(X, reg.predict(X), color='#6D8F18', linewidth=2)
plt.grid(False)
plt.xlabel('xlabel',font)
plt.ylabel('ylabel',font)
plt.show()#
# 打印模型参数和预测结果
print('模型参数:', reg.coef_, reg.intercept_)
print('预测结果:', y_new)本文对于Python实现线性回归算法进行了详细的介绍。首先,我们介绍了线性回归的概念和原理,然后介绍了它的应用场景。最后,我们使用 scikit-learn 库来实现了线性回归算法,并对结果进行了可视化。

相关文章:

机器学习之线性回归
往期目录 python在线性规划中的应用 文章目录 一、线性回归算法概述1.1 什么是线性回归?1.2 线性回归算法原理1.3 线性回归的应用场景 二、线性回归算法Python实现2.1 导入必要的库2.2 随机生成数据集2.3 拟合模型2.4 预测结果2.5 结果可视化 三、完整代码 线性回归…...

中国系统正式发声!所有用户永久免费,网友:再见了,CentOS!
点关注公众号,回复“1024”获取2TB学习资源! 如果说:没有操作系统会怎么样? 对于个PC来说,无论是台式机、笔记本、平板等等,一切都变的一无是处,这些硬件对我们来说,和一堆废铁没什么…...

Oracle数据库坏块类故障
正常的数据块有其特有的固定格式,如果某数据块内部出现了混乱而导致Oracle无法读取,则可称其为坏块。数据库坏块的影响范围可大可小,严重时会导致数据库无法打开。当数据库出现坏块时,一般出现ORA-01578错误、ORA-10632错误或者OR…...

andorid之摄像头驱动流程--MTK平台
camera成像原理: 景物通过镜头生产光学图像投射到sensor表面上,然后转为模拟电信号,经过数模变成数字图像信号,在经过DSP加工出来,然后在通过IO接口传输到CPU处理。 由于摄像头满足总线、驱动、设备模型,…...

Android9.0 iptables用INetd实现屏蔽ip黑名单的实现
1.前言 在9.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置屏蔽ip地址之内的功能,liunx中iptables命令也是比较重要的,接下来就来在INetd这块实现屏蔽ip黑名单的的相关功能,就是在app中只能屏蔽某个网址,就是除了这个网址,其他的都能上网,最后…...

介绍一下json
目录 介绍一下json Elasticsearch7.6学习指南 介绍一下json JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,它以易于阅读和编写的文本形式表示结构化数据。JSON最初是由Douglas Crockford在2001年提出的,它在we…...

DI依赖注入环境
1.构造器注入 上一章节已经说过了: <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLoca…...

《程序员面试金典(第6版)》面试题 16.18. 模式匹配(暴力破解 + 剪枝)
题目描述 你有两个字符串,即pattern和value。 pattern字符串由字母"a"和"b"组成,用于描述字符串中的模式。 例如,字符串"catcatgocatgo"匹配模式"aabab"(其中"cat"是"a&q…...
一天吃透SpringCloud面试八股文
1、什么是Spring Cloud ? Spring cloud 流应用程序启动器是基于 Spring Boot 的 Spring 集成应用程序,提供与外部系统的集成。Spring cloud Task,一个生命周期短暂的微服务框架,用于快速构建执行有限数据处理的应用程序。 Sprin…...

java生成图片缩略图
目录 前言一、使用Base64编码方式1、基本方法2、压缩本地图片保存到本地3、压缩网络图片到图片服务器 二、使用thumbnailator工具方式1、导入依赖2、压缩本地图片保存到本地 前言 下面介绍了两种获取图片缩略图的方式,全都不是一次性压缩,如果没有达到设…...
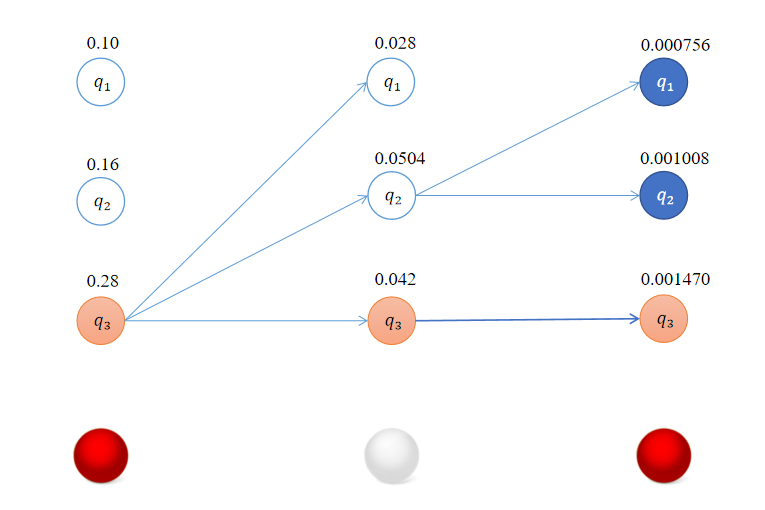
《统计学习方法》——隐马尔可夫模型(下)
学习算法 HMM的学习,在有观测序列的情况下,根据训练数据是否包含状态序列,可以分别由监督学习算法和无监督学习算法实现。 监督学习算法 监督学习算法就比较简单,基于已有的数据利用极大似然估计法来估计隐马尔可夫模型的参数。…...

Liunx top 命令详解
文章目录 top补充说明语法选项top交互命令实例 top 显示或管理执行中的程序 补充说明 top命令 可以实时动态地查看系统的整体运行情况,是一个综合了多方信息监测系统性能和运行信息的实用工具。通过top命令所提供的互动式界面,用热键可以管理。 语法…...

基于 SpringBoot 的医院固定资产系统
本文将介绍基于 SpringBoot 技术的医院固定资产系统的设计和实现。医院固定资产管理是医疗机构管理工作的重要组成部分,它对医院的正常运营和管理具有重要的意义。本系统的设计和实现将有助于医疗机构更好地管理和维护其固定资产。 1. 系统需求分析 医院固定资产管…...

【企业信息化】第2集 免费开源ERP: Odoo 16 销售管理系统
文章目录 前言一、概览二、使用功能1.通过清晰报价提高销售效率2.创建专业报价单3.管理订单及合同4.简化沟通5.维护产品&价格6.直观的报告7.集成 三、总结 前言 世界排名第一的免费开源ERP: Odoo 16 销售管理系统。通过Odoo Sign应用程序和在线支付,发送报价。…...

浅谈数据治理
大家好 ,近年来,数据治理成为挖掘数据价值的重要手段和工具。随着大数据平台和工业互联网兴起,数据治理平台主要采用数据中台技术和微服务架构初步替代传统架构,面向大数据架构下,为数据资源中心与外部数据系统提供数据…...

Matlab入门教程003|MATLAB变量|MATLAB命令
MATLAB变量 每个MATLAB变量可以是数组或者矩阵。 用一个简单的方法指定变量。例如: x 3 % defining x and initializing it with a value MATLAB执行上述语句,并返回以下结果: x 3 上述的例子创建了一个1-1的矩阵名为x和的值存储…...

【啃书C++Primer5】-编写一个简单C++程序
每个C程序都包含一个或多个函数(function),其中一个必须命名为main。操作系统通过调用main来运行C程序。下面是一个非常简单的main函数,它什么也不干,只是返回给操作系统一个值: int main() {return 0; }一个函数的定义包含四部分:返回类型(r…...
GoView 是一个Vue3搭建的低代码数据可视化开发平台
一、总览 开源、精美、便捷的「数据可视化」低代码开发平台 二、整体介绍 框架:基于 Vue3 框架编写,使用 hooks 写法抽离部分逻辑,使代码结构更加清晰; 类型:使用 TypeScript 进行类型约束,减少未知错误…...

【面试篇】Redis持久化面试题
文章目录 Redis持久化🙎♂️面试官:什么是Redis持久化? AOF日志AOF日志原理🙎♂️面试官:AOF日志是怎么工作的/AOF写入磁盘的流程?🙎♂️面试官: 刚刚说到了Redis先执行写入的…...
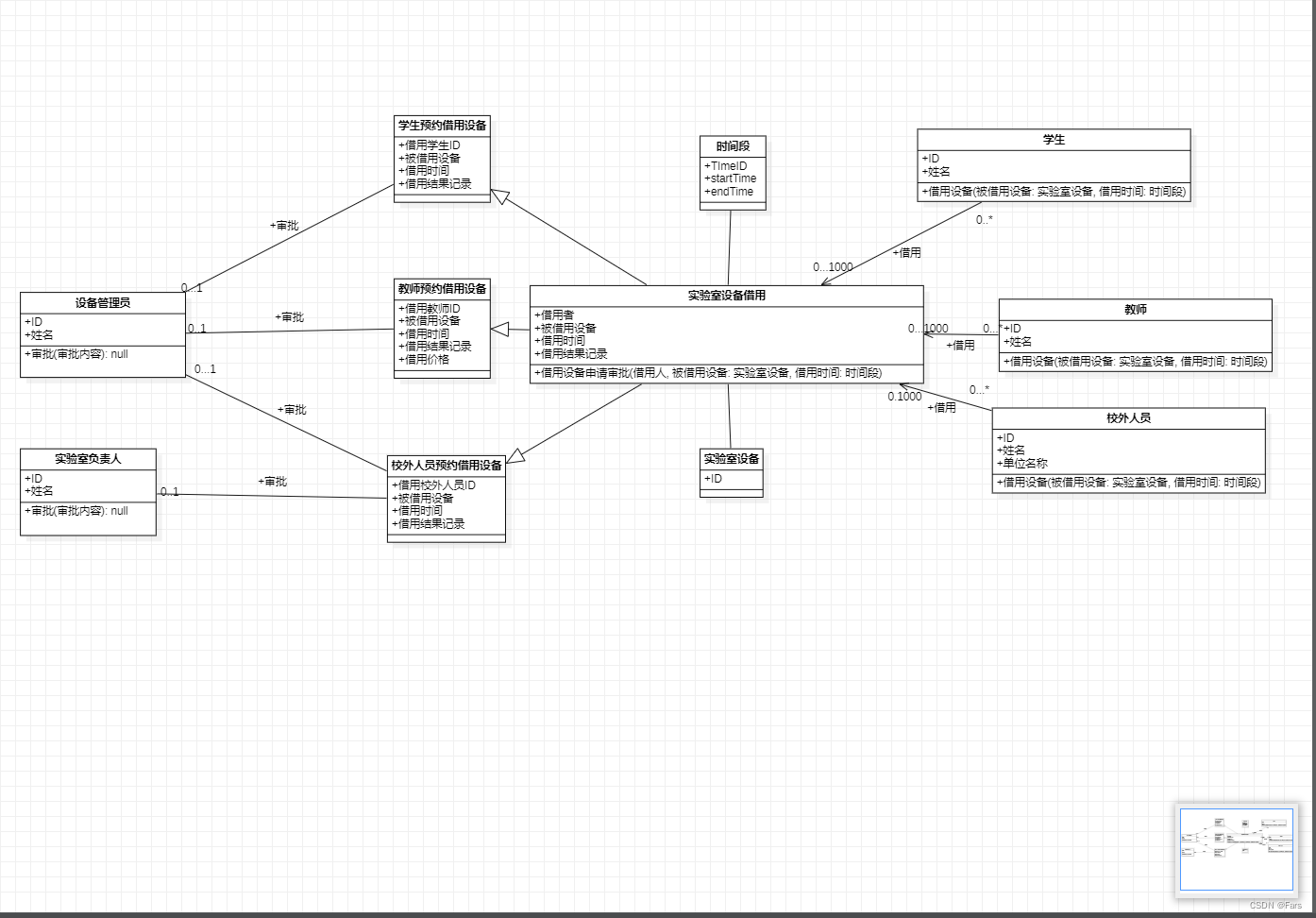
哈工大软件过程与工具作业2
云原生技术云原生技术 哈尔滨工业大学 计算机科学与技术学院/国家示范性软件学院 2022年秋季学期 《软件过程与工具》课程 作业报告 作业 2:需求分析UML建模 姓名 学号 联系方式 石卓凡 120L021011 944613709qq.com/18974330318 目 录 1 需求概述...........…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
