进行性能压力测试的原因、目的和好处
性能压力测试是指在模拟高负载、高并发情况下对软件系统进行测试,以衡量系统在实际使用过程中的性能表现。这些测试可以为生产环境中的应用程序提供关键数据,并帮助开发人员从根本上了解系统的实际性能。在本文中,我们将探讨进行性能压力测试的原因、目的和好处。

为什么需要进行性能压力测试?
在今天的市场竞争中,软件质量和性能是至关重要的。随着互联网、移动应用和云计算等技术的日益普及,用户对系统的性能和稳定性的要求越来越高。在这种情况下,由于各种因素导致不良性能,例如大流量或高并发,可能会导致系统崩溃和发生重大故障。
而性能压力测试是一种评估系统性能表现并确定其最大负载容量的过程。通过并行模拟真实的应用程序操作,性能压力测试可为开发人员提供有关系统的稳定性、吞吐量、响应时间和缓存能力等方面的综合信息。以下是进行性能压力测试的一些原因:
发现系统瓶颈:压力测试可以确定给定系统的最大负载容量和其在高负载条件下的性能瓶颈。测试可以帮助发现系统中的性能问题,例如未预期的延迟或请求丢失。
确定系统可伸缩性:压力测试可以确定您的系统在处理更多请求时是否会出现延迟或崩溃。这帮助您确定您需要从系统角度进行的任何更改,例如添加其他硬件资源和分布式计算。
建立信心:通过测试,您可以确保您的应用程序能够处理更多的负载,而不会出现应用或服务中断。这有助于您更好地打造品牌和提高用户满意度。

性能压力测试的好处
提高应用程序性能:性能压力测试可以帮助在实际应用程序负载下发现和消除性能瓶颈。它可以帮助检测内存泄漏、线程问题、资源争用等,并导致系统性能下降。
降低风险:在生产环境中,在正式推出之前进行性能压力测试,可以发现可能出现的问题,从而降低出现故障的风险。
提高用户满意度:在性能压力测试期间,开发人员可以确定系统的吞吐量和响应时间等方面的最佳性能。这可以确保系统在遇到繁忙时仍能高效运行,从而提高用户的满意度。
总结
在竞争激烈的市场中,强大的系统性能和稳定性是高水平、高竞争力的软件的关键。通过进行性能压力测试,开发人员可以发现和解决性能问题,并确定系统的最大负载容量。这不仅可以为生产环境中的应用程序提供保障,而且还有助于提高用户满意度,将品牌打造到一个更高的层面。
相关文章:

进行性能压力测试的原因、目的和好处
性能压力测试是指在模拟高负载、高并发情况下对软件系统进行测试,以衡量系统在实际使用过程中的性能表现。这些测试可以为生产环境中的应用程序提供关键数据,并帮助开发人员从根本上了解系统的实际性能。在本文中,我们将探讨进行性能压力测试…...
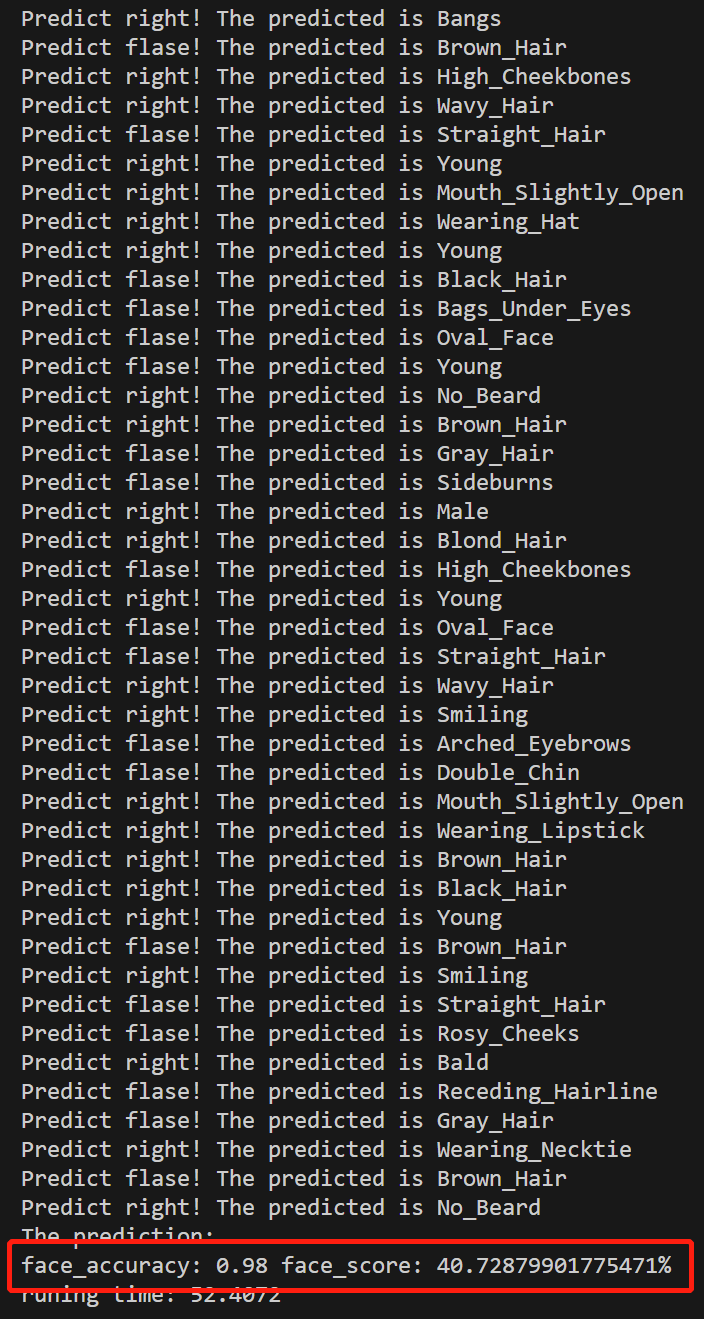
【计算机视觉】如何利用 CLIP 做简单的人脸任务?(含源代码)
文章目录 一、数据集介绍二、源代码 结果三、代码逐行解读 一、数据集介绍 CELEBA 数据集(CelebFaces Attributes Dataset)是一个大规模的人脸图像数据集,旨在用于训练和评估人脸相关的计算机视觉模型。该数据集由众多名人的脸部图像组成&a…...

基于显扬科技3D视觉相机的医疗试管分拣系统
行业现状: 医疗试管分拣是医疗行业中的一个重要环节,指将医疗实验室或生物技术研究中的试管按照一定的规则进行分拣,并对试管的类型、位置、数量等信息进行识别和管理。 随着医疗技术的不断发展和诊断治疗的精细化,医疗试管分拣…...
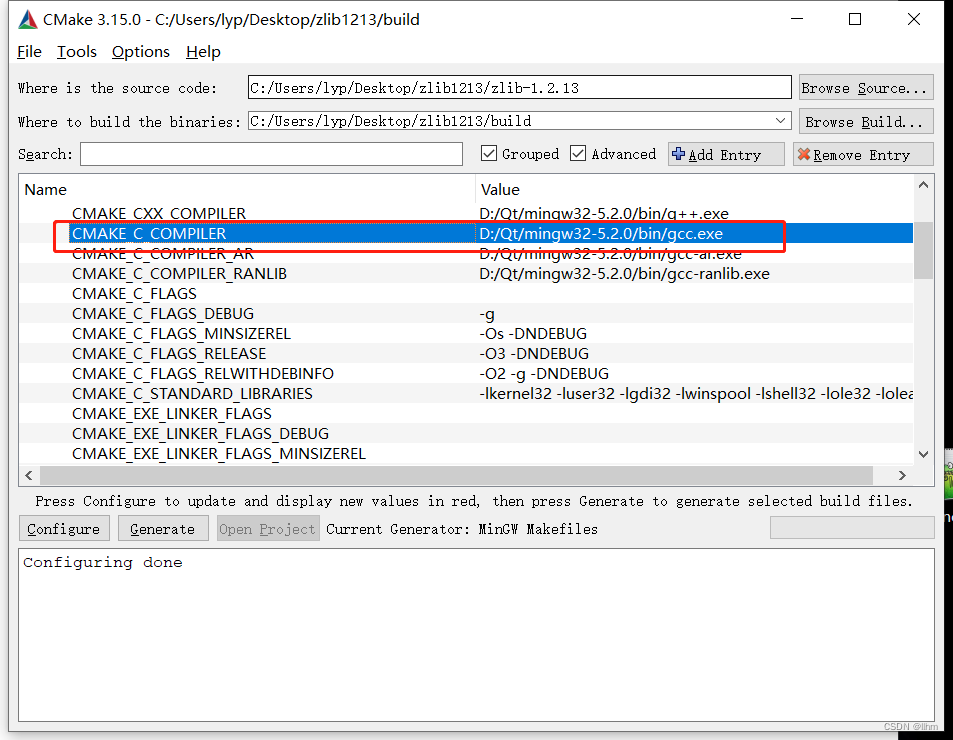
编译zlib
zlib被设计为一个免费的,通用的,法律上不受限制的-即不受任何专利保护的无损数据压缩库,几乎可以在任何计算机硬件和操作系统上使用。 官网:http://www.zlib.net/ 下载zlib源码:http://www.zlib.net/zlib1213.zip 备用地址&#x…...

如何让“ChatGPT自己写出好的Prompt的“脚本在这里
写个好的Prompt太费力了 在网上,你可能会看到很多人告诉你如何写Prompt,需要遵循各种规则,扮演不同的角色,任务明确、要求详细,还需要不断迭代优化。写一个出色的Prompt需要投入大量的时间和精力。甚至有一些公开的Pr…...

菜单选择shell
[rootes3 data]# vi action.sh #!/bin/bash . /etc/init.d/functionsecho -en "\E[$[RANDOM%731];1m"cat <<EOF请选择:1) 备份数据库2)清理日志3)软件升级4)软件回滚5)删库跑路EOFecho -en \E[0mread -p "请选择上面的项对应的数字1-5…...
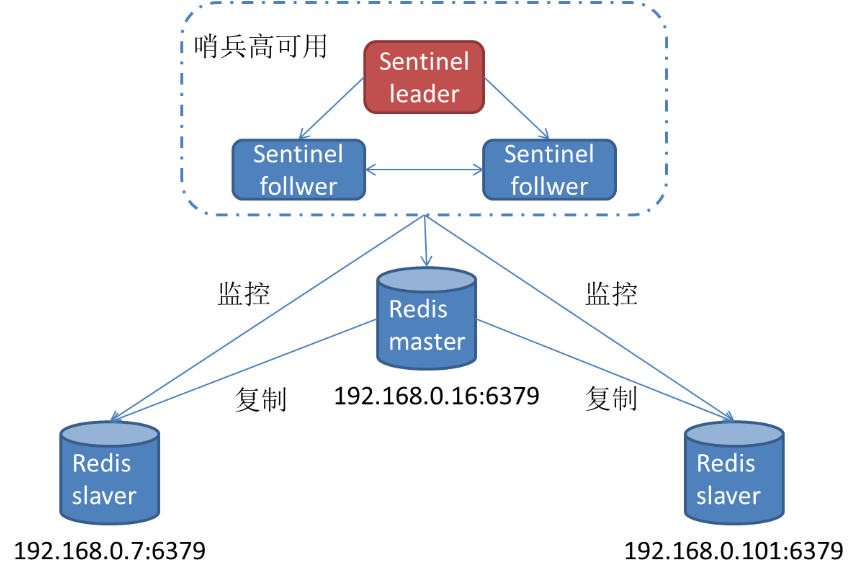
Redis高可用性详解
目录 编辑 高可用性: 主从复制(Master-Slave Replication): 主从复制的一般工作流程: 哨兵模式(Sentinel Mode): 哨兵模式的一般工作流程: 集群模式(…...
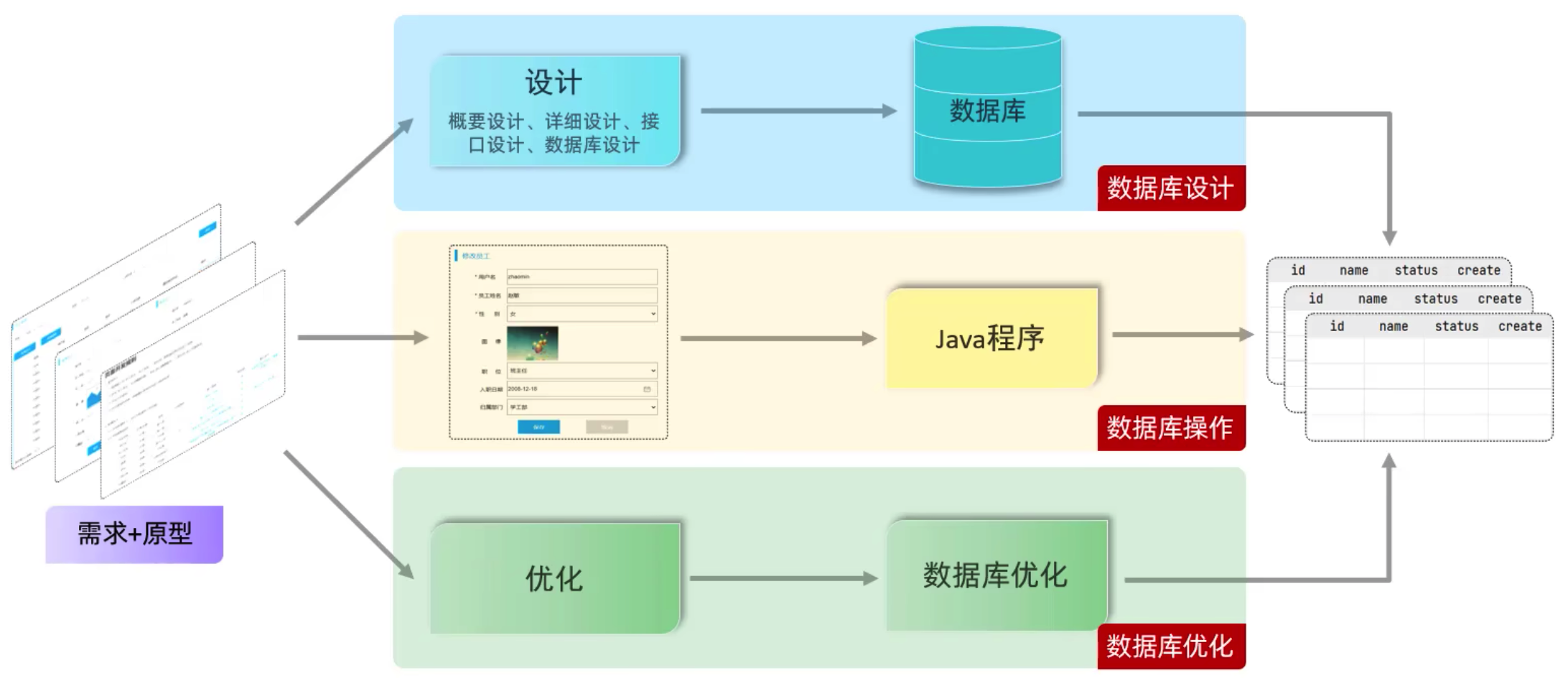
MySQL(1) ---- 数据库介绍与MySQL概述
介绍 1、什么是数据库? 数据库:DateBase(DB),是存储和管理数据的仓库。数据库管理系统:DataBase Management System(DBMS),操纵和管理数据库的大型软件。SQL࿱…...

面试题之软件测试流程
说说公司的软件测试流程,这,是常考的面试题之一。 不同公司的流程不一样,现状决定流程,没有绝对的对错。 以结果为导向,保证产品质量,提高测试效率,才是王道。 以下的流程为业界比较标准的流程&…...

MyBatis中#{}与${}的区别,与各自的应用场景
#{}和${}的区别: #{}: 底层使用PreparedStatement。特点:先进行SQL语句的编译,然后给SQL语句的占位符问号?传值。可以避免SQL注入的风险。 ${}:底层使用Statement。特点:先进行SQL语句的拼接,然后再对SQL语…...

泛型类相关
package com.test.test02;/* * GenericTest就是一个普通的类 * GenericTest<E>就是一个泛型类 * <>里面就是一个参数类型,但是这个类型是什么呢?这个类型现在是不确定的,相当于一个占位。 * 但是现在确定的是这个类型一定是一…...

一文速学数模-季节性时序预测SARIMA模型详解+Python实现
目录 前言 一、季节时间序列模型概述 二、SARIMA模型定义 三.SARIMA模型算法原理...
)
二叉树与图(C++刷题笔记)
二叉树与图(C刷题笔记) 113. 路径总和 II 力扣 从根节点深度遍历二叉树,先序遍历时,将节点存储至path栈中,使用path_val累加节点值 当遍历到叶子节点,检查path_val是否为sum,若是,…...
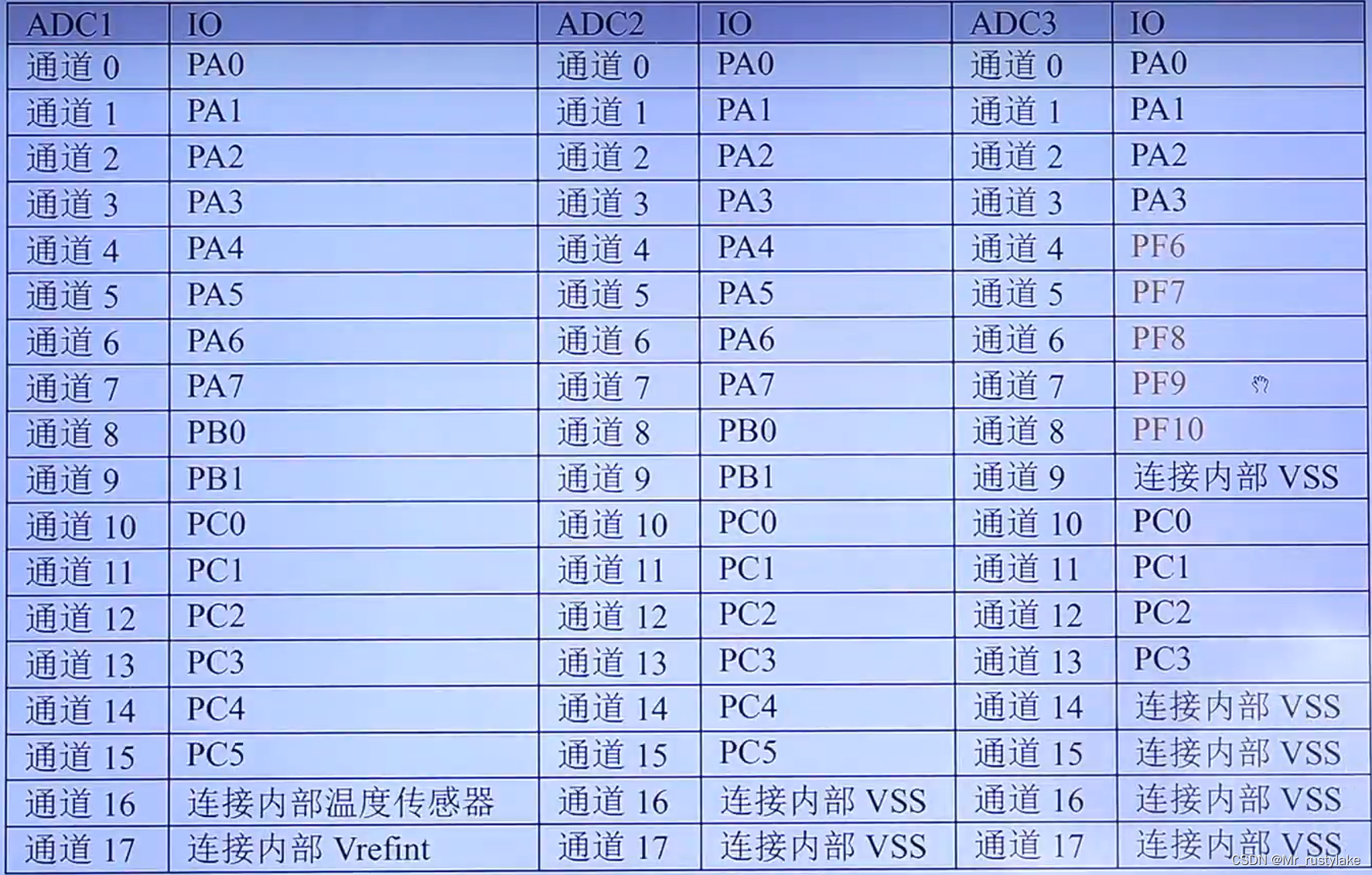
STM32-ADC多通道输入实验
之前已经介绍了几个ADC的笔记和实验了,链接如下: 关于ADC的笔记1_Mr_rustylake的博客-CSDN博客 STM32-ADC单通道采集实验_Mr_rustylake的博客-CSDN博客 STM32-单通道ADC采集(DMA读取)实验_Mr_rustylake的博客-CSDN博客 接下来…...
javaIO流之文件流
目录 简介一、File的构造方法二、File的常用方法1、获取功能的方法2、绝对路径和相对路径3、判断功能的方法4、创建、删除功能的方法5、目录的遍历6、递归遍历 三、RandomAccessFile1、主要方法 四、Apache FileUtils 类1、复制文件或目录:2、删除文件或目录&#x…...

DMA-STM32
DMA-STM32 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预,节省了CPU的资源 12个独立可配置的通道:DMA1 (7个通道),DMA2 (5个通道) 每个通道都支持软件触发和特定的硬件触发 STM32…...

代码随想录算法训练营第二十七天|39. 组合总和、40.组合总和II、131.分割回文串
目录 39. 组合总和 40.组合总和II 131.分割回文串 39. 组合总和 本题是 集合里元素可以用无数次,那么和组合问题的差别 其实仅在于 startIndex上的控制 题目链接/文章讲解:代码随想录 视频讲解:带你学透回溯算法-组合总和(对应…...
 <? extends T>,<? super T>)
泛型(Generic) <? extends T>,<? super T>
通配符边界引入背景 使用泛型的过程中,经常出现一种很别扭的情况。我们有 Fruit 类,和它的派生类 Apple 类。 class Fruit {}class Apple extends Fruit {}然后有一个最简单的容器:Plate 类。盘子里可以放一个泛型的 “东西”. class Plat…...

数云融合|数字化转型中的利器:揭秘云技术的重要角色
数字化转型不仅是一个流行语,而是一项真正能够改变你的业务流程并提高客户参与度的重要战略。要实现数字化转型,必须重新构建业务流程,同时利用AI、物联网、AR、ML、大数据分析等先进技术不断提升客户参与度。这就需要利用云技术提供的强大计…...

Linux篇2
Linux 0. 终端提示信息1. 文件目录结构1.1 文件目录 2. 文本编辑器VI/VIM2.1 VIM编辑器2.1 一般模式2.2 编辑模式2.3 命令模式 3. 网络配置3.1 VMware提供的三种网络连接模式3.2 静态配置网络IP地址3.3 配置主机名3.3.1 修改主机名3.3.2 配置主机名-IP地址映射关系:…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

第2课 SiC MOSFET与 Si IGBT 静态特性对比
2.1 输出特性对比 2.2 转移特性对比 2.1 输出特性对比 器件的输出特性描述了当温度和栅源电压(栅射电压)为某一具体数值时,漏极电流(集电极电流...

第6章:Neo4j数据导入与导出
在实际应用中,数据的导入与导出是使用Neo4j的重要环节。无论是初始数据加载、系统迁移还是数据备份,都需要高效可靠的数据传输机制。本章将详细介绍Neo4j中的各种数据导入与导出方法,帮助读者掌握不同场景下的最佳实践。 6.1 数据导入策略 …...
