【人工智能】蚁群算法(密恐勿入)
蚁群算法(密恐勿入)
蚁群算法--给你一个感性认识
- 蚁群算法(密恐勿入)
- 1. 算法简介
- 1.1 基本原理
- 1.1.1 模拟蚂蚁在简单地形,寻找食物
- 1.1.2 模拟蚂蚁在复杂地形,找到食物
- 1.2 算法应用
- 2. 算法解析
- 3.算法应用——TSP问题
- 3.1 TSP旅行商介绍
- 3.2 利用蚁群算法解决TSP问题
- 总结一下:
1. 算法简介
1.1 基本原理
蚁群算法是一种模拟蚂蚁觅食行为的启发式算法,被广泛应用于优化问题的求解。蚁群算法的基本思想是,将一群蚂蚁放在问题的解空间上,让它们通过信息素的传递和挥发,逐渐找到最优解。
1.1.1 模拟蚂蚁在简单地形,寻找食物

阶段一:在蚁群算法的初始阶段,我们在地图上不放置任何食物,因为蚂蚁需要在没有任何信息素的情况下开始摸索前进。一开始,蚂蚁们在洞外随机移动,试图找到食物的位置。每只蚂蚁的速度相同,它们会按照随机的方向前进,直到遇到障碍物或者到达了边界。此时,它们会再次随机选择一个方向,并继续前进。这个过程会持续进行,

阶段二:当蚂蚁们找到了食物后,它们会将一些信息素沿着它们的路径释放出来,并且在回到蚁巢的路上也会释放信息素。
蚁群之间的规则:
- 蚂蚁发现食物并将其带回巢穴时,通常会遵循已经标记的路径返回,即原路返回。在返回过程中,蚂蚁会释放归巢素和信息素,这些化学物质可以吸引其他蚂蚁跟随它的路径前往食物源。如果路径上有较多的归巢素或信息素,则越来越多的蚂蚁将会选择这条路径前往食物。
阶段三:当蚂蚁们回到巢穴时,它们会在原来的路径上释放更多信息素,增强这条路径的吸引力,并且尝试着寻找更短的路径。蚂蚁们会在路径上选择合适的地方停下来,释放信息素,然后返回巢穴。这个过程将持续进行,直到蚂蚁们找到了最优路径。
根据以上规则,随着时间的推移,蚂蚁们终会(可能)找到的最优路径。

1.1.2 模拟蚂蚁在复杂地形,找到食物


1.2 算法应用
蚁群算法已经应用于多种优化问题的求解,比如:
- 旅行商问题
- 图着色问题
- 网络路由问题
- 调度问题
- 生产计划问题
在这些问题中,蚁群算法通常能够找到较优的解。此外,蚁群算法还可以用于机器学习领域中的聚类和分类等问题。
2. 算法解析
想要理解算法?需要去理解以下内容:
- 蚁群是如何找到解的?解的步骤是什么?
- 蚂蚁在初始时随机选择一个起点,并向前行走。
- 当蚂蚁走到一个节点时,它会选择一个下一个节点进行移动。蚂蚁选择下一个节点的概率与该节点上的信息素浓度成正比。信息素浓度越高的节点,被选择的概率也越高。
- 当蚂蚁移动到一个节点时,它会在该节点上释放一定量的信息素。
- 当蚂蚁找到解后,它会回到起点,并在路径上释放更多的信息素,增强这条路径的吸引力。
- 当其他蚂蚁在寻找解的过程中遇到已经被标记的路径时,它们会更有可能选择这条路径。
- 随着时间的推移,信息素会挥发,路径上信息素的浓度会逐渐降低。这样,路径上的信息素浓度会经历一个上升和下降的过程。
- 蚂蚁们会根据路径上的信息素浓度来选择下一个节点。当信息素浓度很高时,它们更有可能选择这条路径。
- 蚂蚁们持续寻找解,直到找到最优解或者达到预设的迭代次数。
蚂蚁个体之间就是通过这种间接的通信机制实现协同搜索最短路径的目标的。我们举例简单说明蚂蚁觅食行为:
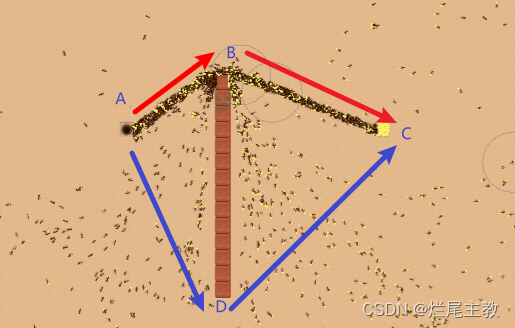
现阶段 蚂蚁有A→B→C 和 A→D→C两种较优路径, A→D→C的距离要大于A→B→C
因为大量蚂蚁的选择概率会不一样,会将蚂蚁大致分为两批,一批走A→B→C ,另一批走A→D→C,单位时间内A→B→C通过蚂蚁也要大于 A→D→C,随着时间的推移,A→B→C的信息素越来越多,正反馈调节下,走此条路径的蚂蚁也越来越多。所以越短路径的浓度会越来越大,经过此短路径达到目的地的蚂蚁也会比其他路径多。这样大量的蚂蚁实践之后就找到了最短路径。所以这个过程本质可以概括为以下几点:
- 路径概率选择机制信息素踪迹越浓的路径,被选中的概率越大
- 信息素更新机制路径越短,路径上的信息素踪迹增长得越快
- 协同工作机制蚂蚁个体通过信息素进行信息交流。
蚂蚁在蚁群算法中通过信息素的传递和挥发来进行交流。通过信息素的传递和挥发,整个蚁群就会产生信息正反馈现象、种群分化等。
-
正反馈现象
由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象。某一路径上走过的蚂蚁越多,则后来者选择该路径的可能性就越大。
💡 在一个人流量比较大的商场,人们往往会选择人流量比较大的走廊或者通道来走,因为人流量越大,越能够说明这个通道是正确的,这样就会产生一种信息正反馈现象,后来的人也会选择这条路线,进一步增加这条路线的人流量。与蚁群算法类似,人们会根据前人的经验来选择路线,从而产生类似的正反馈现象。
-
种群分化
种群分化是蚁群算法中的一个现象,当蚂蚁在搜索过程中遇到了局部最优解时,会一直围绕这个局部最优解寻找,并且释放信息素。这会导致其他蚂蚁也会被吸引过来,导致整个蚁群陷入局部最优解,而无法找到全局最优解的情况。这种现象在蚁群算法中是非常常见的,需要特别注意。为了避免种群分化,蚂蚁需要具有一定的随机性,同时需要及时更新信息素,以便发现全局最优解。
💡一个人在某个领域上有很高的专业技能,但是如果他过于专注于这个领域,就可能会失去对其他领域的了解和认识,进而导致对问题的认识出现偏差,甚至无法解决某些问题。
就比如图1. 我如果此刻将原有阻碍去掉一部分,此时只靠信息素交流的蚁群会产生种群分化现象。陷入了局部最有解。

当蚁群算法陷入局部最优解时,可以使用以下方法进行优化:
- 增加蚂蚁的数量。增加蚂蚁的数量可以增加搜索的广度,从而有更大的可能性找到全局最优解。
- 调整信息素挥发速度。通过适当降低信息素挥发速度,可以增加信息素在路径上的积累,从而增加蚂蚁选择该路径的概率。
- 引入随机因素。在蚁群算法中引入随机因素,可以使蚂蚁更具有探索性,从而有可能跳出局部最优解,进而找到全局最优解。
- 改变参数。通过改变蚁群算法中的参数,如信息素浓度、信息素挥发速度、启发式因子等,可以使算法更加灵活,从而更容易找到全局最优解。
- 使用局部搜索算法。在蚁群算法的基础上,可以结合局部搜索算法,如模拟退火算法、遗传算法等,来寻找全局最优解。
上述的情况,可以利用第三条和第四条解决。
3.算法应用——TSP问题
3.1 TSP旅行商介绍
首先,我们先回顾一下,什么是TSP旅行商问题:

假设有一位邮递员,他从初始城市(任意一城市)出发,途径所有城市并回到初始城市,那么他一共会有
( n − 1 ) ! (n-1)! (n−1)!
条路径。从中找出那条最短路径,这就是TSP旅行商问题。
如果我们遍历的去找那个最短路径,那么随着城市的增加,计算量大大增加。

3.2 利用蚁群算法解决TSP问题
在这里,蚂蚁仅有信息素这一项能力是不够的。所以我们给与蚂蚁一些其他的能力
- 蚂蚁在一次旅行中不会重复访问相同的城市
- 蚂蚁可以知晓城市之间的距离。
- 蚂蚁在路上会释放信息素
- 蚂蚁在选择下一个城市的概率依靠以下公式:
p i j k = ( τ i j α ) ( η i j β ) ∑ allowed k ( τ i j α ) ( η i j β ) p_{i j}^{k}=\frac{\left(\tau_{i j}^{\alpha}\right)\left(\eta_{i j}^{\beta}\right)}{\sum_{\text {allowed}_k}\left(\tau_{i j}^{\alpha}\right)\left(\eta_{i j}^{\beta}\right)} pijk=∑allowedk(τijα)(ηijβ)(τijα)(ηijβ)
| 参数名称 | 参数意义 | 参数设置过大 | 参数设置过小 |
|---|---|---|---|
| 信息素因子ɑ | 反映了蚂蚁运动过程中路径上积累的信息素的量在指导蚁群搜索中的相对重要程度。取值范围通常在[1, 4]之间。 | 蚂蚁选择以前已经走过的路可能性较大,容易使随机搜索性减弱 | 蚁群易陷入纯粹的随机搜索,使种群陷入局部最优 |
| 启发函数因子𝛽 | 反映了启发式信息在指导蚁群搜索中的相对重要程度,蚁群寻优过程中先验性、确定性因素作用的强度取值范围在[0, 5]之间 | 虽然收敛速度加快,但是易陷入局部最优 | 蚁群易陷入纯粹的随机搜索,很难找到最优解 |

其实这个公式也很好理解,蚂蚁选择城市的概率主要由 τ i j ( t ) \tau_{ij}(t) τij(t)和 η i j ( 𝑡 ) \eta_{ij}(𝑡) ηij(t)有关,分母为蚂蚁k可能访问的城市之和(为常数),这样才能使蚂蚁选择各个城市的概率之后为1,符合概率的定义。 τ i j ( t ) \tau_{ij}(t) τij(t)和$\eta_{ij}(𝑡)上的指数信息素因子ɑ和启发函数因子𝛽只决定了信息素浓度以及启发函数对蚂蚁k从i到j的可能性的贡献程度。
例:下图为计算蚂蚁从起点城市2到可达城市的概率(套公式,很好理解):

图2. 此图和此节部分内容借鉴于秃头小苏:蚁群算法(实例帮助理解)
OK,蚂蚁有了这些能力后,我们只需要控制一下流程,就可以解决TSP问题了,下面是给出了此问题的一种常用的解决流程
蚁群算法解决TSP问题的算法流程
- 初始化信息素浓度矩阵 τ i j ( t ) \tau_{ij}(t) τij(t),启发式函数 η i j \eta_{ij} ηij,以及蚂蚁的位置。
- 每只蚂蚁按照信息素和启发式函数的概率选择下一个城市。
- 记录蚂蚁的路径和距离。
- 在所有蚂蚁走完所有城市之后,根据蚂蚁走过的路径和距离更新信息素浓度矩阵 η i j ( t ) \eta_{ij}(t) ηij(t)。
- 如果未达到停止条件,则返回步骤2。
其中,停止条件可以是迭代次数达到预设值或者最佳解不再改变。
起点的选择对最短路径是有影响的。不同的起点可能会导致不同的最短路径。在蚁群算法中,通过随机选择起始点,可以增加搜索的广度,从而有更大的可能性找到全局最优解。
信息素更新的时机一般有两种方式:
- 在每个迭代周期结束后进行更新,即在所有蚂蚁完成当前迭代周期后,根据其路径长度和信息素更新信息素浓度。
- 在每只蚂蚁走遍所有城市之后,立即更新信息素浓度。
信息素更新公式:
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ k = 1 m Δ τ i j k ( t ) \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\sum_{k=1}^{m} \Delta \tau_{i j}^{k}(t) τij(t+1)=(1−ρ)τij(t)+k=1∑mΔτijk(t)
其中, ρ \rho ρ 是信息素挥发速度, Δ τ i j k ( t ) \Delta \tau_{i j}^{k}(t) Δτijk(t) 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,m 是蚂蚁的数量。
在每个迭代周期结束后进行更新或在每只蚂蚁走遍所有城市之后立即更新信息素浓度均可。
Delta tau 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,不同的 Delta tau 规则有以下几种:
- 静态规则:所有蚂蚁在搜索过程中释放的信息素量是相等的,即 Δ τ i j k ( t ) = Q / L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t) Δτijk(t)=Q/Lk(t),其中 Q 是常量,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 动态规则:蚂蚁在搜索过程中释放的信息素量是动态变化的,即 Δ τ i j k ( t ) = Q / L k ( t ) + ∑ k = 1 m w k ⋅ L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t)+\sum_{k=1}^{m} w_{k} \cdot L_{k}(t) Δτijk(t)=Q/Lk(t)+∑k=1mwk⋅Lk(t),其中 ∑ k = 1 m w k = 1 \sum_{k=1}^{m} w_{k}=1 ∑k=1mwk=1,w_k 是蚂蚁 k 对信息素的贡献系数,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 最大值规则:每只蚂蚁在搜索过程中释放的信息素量最多为 Δ τ i j k ( t ) = Q L b e s t \Delta \tau_{i j}^{k}(t)=\frac{Q}{L_{best}} Δτijk(t)=LbestQ,其中 L_best 是迄今为止找到的最短路径长度。
以上规则中,静态规则是最简单的,但是可能会导致信息素的浓度过高或过低,从而影响搜索效果。动态规则可以根据搜索的进展情况动态调整信息素的浓度,适应性更强。最大值规则可以防止信息素浓度过高,但可能会导致搜索无法跳出局部最优解。
例(静态规则):下图为信息素的更新过程,假设初始时各路径信息素浓度为10。

总结一下:
蚁群算法流程:
- 初始化信息素浓度矩阵𝜏_{ij}(t),启发式函数𝜂_{ij},以及蚂蚁的位置。
- 每只蚂蚁按照信息素和启发式函数的概率选择下一个城市。
- 记录蚂蚁的路径和距离。
- 在所有蚂蚁走完所有城市之后,根据蚂蚁走过的路径和距离更新信息素浓度矩阵𝜏_{ij}(t)。
- 如果未达到停止条件,则返回步骤2。
其中,停止条件可以是迭代次数达到预设值或者最佳解不再改变。
起点的选择对最短路径是有影响的。不同的起点可能会导致不同的最短路径。在蚁群算法中,通过随机选择起始点,可以增加搜索的广度,从而有更大的可能性找到全局最优解。
信息素更新的时机一般有两种方式:
- 在每个迭代周期结束后进行更新,即在所有蚂蚁完成当前迭代周期后,根据其路径长度和信息素更新信息素浓度。
- 在每只蚂蚁走遍所有城市之后,立即更新信息素浓度。
信息素更新公式:
τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ k = 1 m Δ τ i j k ( t ) \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\sum_{k=1}^{m} \Delta \tau_{i j}^{k}(t) τij(t+1)=(1−ρ)τij(t)+k=1∑mΔτijk(t)
其中, ρ \rho ρ 是信息素挥发速度, Δ τ i j k ( t ) \Delta \tau_{i j}^{k}(t) Δτijk(t) 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,m 是蚂蚁的数量。
在每个迭代周期结束后进行更新或在每只蚂蚁走遍所有城市之后立即更新信息素浓度均可。
Delta tau 是蚂蚁 k 在迭代 t 中走过路径 i 到 j 所留下的信息素,不同的 Delta tau 规则有以下几种:
- 静态规则:所有蚂蚁在搜索过程中释放的信息素量是相等的,即 Δ τ i j k ( t ) = Q / L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t) Δτijk(t)=Q/Lk(t),其中 Q 是常量,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 动态规则:蚂蚁在搜索过程中释放的信息素量是动态变化的,即 Δ τ i j k ( t ) = Q / L k ( t ) + ∑ k = 1 m w k ⋅ L k ( t ) \Delta \tau_{i j}^{k}(t)=Q/L_{k}(t)+\sum_{k=1}^{m} w_{k} \cdot L_{k}(t) Δτijk(t)=Q/Lk(t)+∑k=1mwk⋅Lk(t),其中 ∑ k = 1 m w k = 1 \sum_{k=1}^{m} w_{k}=1 ∑k=1mwk=1,w_k 是蚂蚁 k 对信息素的贡献系数,L_k(t) 是蚂蚁 k 在迭代 t 中走过的路径长度。
- 最大值规则:每只蚂蚁在搜索过程中释放的信息素量最多为 Δ τ i j k ( t ) = Q L b e s t \Delta \tau_{i j}^{k}(t)=\frac{Q}{L_{best}} Δτijk(t)=LbestQ,其中 L_best 是迄今为止找到的最短路径长度。
相关文章:

【人工智能】蚁群算法(密恐勿入)
蚁群算法(密恐勿入) 蚁群算法--给你一个感性认识 蚁群算法(密恐勿入)1. 算法简介1.1 基本原理1.1.1 模拟蚂蚁在简单地形,寻找食物1.1.2 模拟蚂蚁在复杂地形,找到食物1.2 算法应用 2. 算法解析3.算法应用——…...
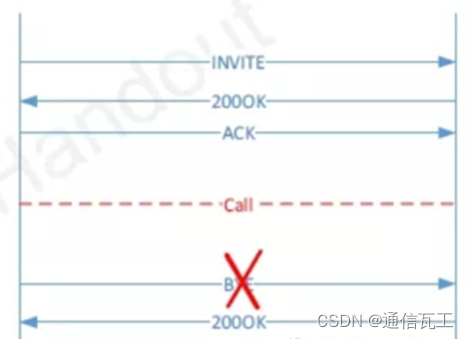
VONR排查指导分享
不能注册或呼叫到SIP服务器端30秒挂断呼叫的黄金法则咬线或摘机状态单通或无语音收到400 bad request收到413,513 Request Entity Too Large或Message Too Large消息收到408, 480或者487 消息483 - Too Many Hops488 – Not Acceptable Here语音质量和思…...

Daftart.ai:人工智能专辑封面生成器
前言 Daft Art AI是一款使用人工智能技术来帮助您制作专辑封面的软件,它可以让您在几分钟内,用简单的编辑器和精选的美学风格,为您的专辑或歌曲创建出惊艳的高质量的艺术品。Daft Art AI有以下几个特点:简单易用:您只…...

ZigBee案例笔记 - 定时器
文章目录 1.片内外设I/O2.定时器简介3.定时器1寄存器4.定时器1操作自由运行模式模模式正计数/倒计数模式 5.16位计数器定时器1控制LED 示例 6.定时器3概述自由运行模式倒计数模式模模式正/倒计数模式 7.定时器3寄存器定时器3控制LED闪烁 1.片内外设I/O 定时器这样的片内外设也…...

GE H201TI 全系统自检和自诊断
Hydran 201Ti是一个小型在线预警发射器。它永久安装在变压器上,将为工作人员提供各种故障气体复合值的单一ppm读数,以提醒他们潜在的问题。 可以下载该值,并且可以将警报设置在预定水平,以提醒人员并能够监控发展中的故障状况。 …...
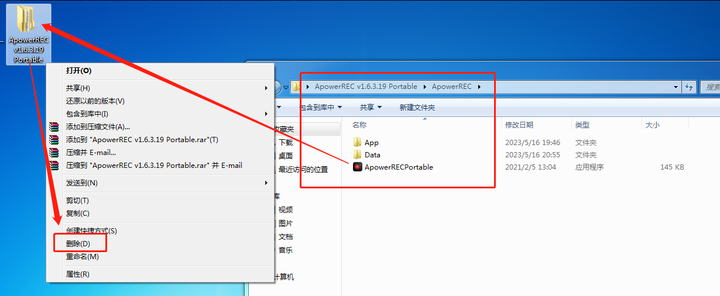
这个屏幕录制太好用了!
哈喽,大家好!今天给各位小伙伴测试了一屏幕录制的小工具——ApowerREC。它是一款专业同步录制屏幕画面及声音的录屏软件。界面简洁,操作简单,支持实时编辑屏幕录像、创建计划任务、录制摄像头高清视频等功能。废话不多说ÿ…...

初识redis【redis的安装使用与卸载】
一.redis的概念 Redis(Remote Dictionary Server ),即远程字典服务,是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。在redis官网中对redis的描述是这样的&#…...

接口测试总结及其用例设计方法整理,希望可以帮到你
目录 接口测试的总结文档 第一部分: 第二部分: 接口测试用例设计 接口测试的总结文档 第一部分:主要从问题出发,引入接口测试的相关内容并与前端测试进行简单对比,总结两者之前的区别与联系。但该部分只交代了怎么做…...

基于FPGA的多功能数字钟的设计
摘要 数字钟是采用数字电路实现对时、分、秒数字显示的计时装置,是人们日常 生活中不可少的必需品。本文介绍了应用FPGA芯片设计多功能数字钟的•种方 案,并讨讨论了有关使用FPGA芯片和VHDL语言实现数字钟设计的技术问题。 关键词数字钟、分频器、译码器、计数器、校时电路、…...
第四十二天学习记录:C语言进阶:笔试题整理Ⅲ
问:解释一下int(*a[20])(int)是什么? ChatAI答: int (*a[20])(int) 是一个数组,该数组中每个元素都是一个指向函数的指针,该函数具有一个int类型的参数,并返回一个int类型的值。 具体来说,a是一…...

GLSL 代码规范
文件 文件顶点,片段,几何和计算着色器文件应该分别有 _vert, _frag, geom 和 _comp 后缀(例如: eevee_film_fragg.glsl)。Shader文件名必须是唯一的,并且必须以它们所属的模块作为前缀(例如: workbench_material_lib.glsl eevee_film_lib.glsl)。一个 shader 文件必须包含且…...

红黑树封装map和set
文章目录 红黑树封装map和set1. 改良红黑树1.1 改良后的节点1.2 改良后的类分别添加仿函数代码 3. 封装map和set3.1 set3.2 map 3. 迭代器3.1 begin 和 end3.2 operator()和operator--()3.3 const迭代器set的迭代器map的迭代器 4. map的operator[]的重载5. 完整代码实现5.1 RBT…...

python序列
在Python中,序列类型包括字符串、列表、元组、集合和字典,这些序列支持以下几种通用的操作,但比较特殊的是,集合和字典不支持索引、切片、相加和相乘操作。 字符串也是一种常见的序列,它也可以直接通过索引访问字符串内…...
LeetCode35. 搜索插入位置(二分法入门)
写在前面: 题目链接:LeetCode35. 搜索插入位置 编程语言:C 题目难度:简单 一、题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会…...
macOS Ventura 13.4 RC3(22F66)发布
系统介绍 5 月 17 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.4 RC 3 更新(内部版本号:22F66),本次更新距离上次发布隔了 5 天。 macOS Ventura 带来了台前调度、连续互通相机、FaceTime 通话接力等功能。其中&…...

CSI和DSI介绍
1、CSI和DSI的接触协议介绍 MIPI、CSI、CCI 协议基础介绍_csi协议_赵哈哈x的博客-CSDN博客 流媒体技术基础-摄像头接口与标准_【零声教育】音视频开发进阶的博客-CSDN博客 《摄像头 —— MIPI CSI-2简介》 USB摄像头使用 — Lichee zero 文档 2、AIO-3288J ,and…...
vue3+antDesignVue前端纯导出
效果 <a-buttonsize"default"style"margin-left: 10px"click"exportData">导出</a-button>1.下载所需依赖 npm install xlsx --save npm install file-saver --save<script setup> import { reactive, ref } from "vue…...

卷积神经网络的剪枝及其在嵌入式视觉系统中的应用
卷积神经网络的剪枝及其在嵌入式视觉系统中的应用 摘要 在过去的十年里,计算机视觉的最新技术一直是由深度神经网络,特别是卷积神经网络所控制的。无论是分类、语义分割还是目标检测,神经网络现在都是一个无可争议的首选。因此,…...

Spring IOC - Bean的初始化
在bean的初始化阶段,bean已经被实例化及属性填充了,此时的bean已相对成熟,接下来的初始化阶段还会做一些额外的工作对bean做进一步处理,主要包括以下四个方面: 调用aware接口方法 初始化前:调用初始化前的…...

Golang 安装
学习目标 本文旨在帮助初学者了解 Golang 在不同环境下的安装方法,并提供相关资源和参考链接。 学习内容 安装 Golang on Windows 下载 Golang for Windows 安装包,地址:https://golang.org/dl/双击运行安装包,按照提示完成安装。配置环境变量: 在系统变量中添加 GOROO…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
