[日记]LeetCode算法·二十五——二叉树⑤ AVL树(插入+删除)附代码实现
本章的代码实现基于上一篇BST与优先队列的基类进行平衡二叉树,即AVL树。
文章目录
- AVL的概念
- AVL查询效率
- AVL的插入
- 1.插入节点
- 2.更新平衡因子BF
- 3.旋转调整树的结构
- 3.1 LL 右旋
- 3.2 RR 左旋
- 3.3 LR 左右双旋
- 3.4 RL 右左双旋
- 4 插入总结
- AVL的删除
- 1.寻找删除节点
- 2.更新平衡因子BF + 旋转
- 3.实际删除节点
- 4.删除总结
- 总结
AVL的概念
总所周知,BST在插入数据随机的情况下,其搜索能达到O(logn)的性能,但如果插入数据有序,或是经过若干次的插入与删除,BST将会退化,甚至变为线性的链表,这不利于搜索。
如何保持BST的优秀查找性质,同时又不至于过分的维护成本(例如完全二叉树),AVL树就是其中一个答案。
AVL树通过维护左右子树高度差,从而保证了搜索的效率,AVL的定义如下:
- AVL树要么是空树,那么满足以下两个条件
- AVL树的左右子树也是AVL树
- AVL节点的平衡因子绝对值不超过1,平衡因子(balance factor)定义:左右子树高度差=左子树高度-右子树高度
AVL查询效率
AVL树的查询效率同样为O(logn),具体证明如下:
使用数学归纳法,假设高度为h的AVL树,其所能容纳的最少节点数为N(h)(即容纳N个节点时,AVL最大即最糟糕的高度),可以发现满足以下情况:
- h=1时,N(h)=1
- h=2时,N(h)=2
- 当h>=3时,最糟糕的树必然根节点BF不为0(因为BF=0时,左右子树都高h-1,容纳节点必然多与1个h-2子树+1个h-1子树),那么此时最糟糕的树= 1个根节点 + 1个h-1的子树 + 1个h-2的子树,即N(h)= 1 + N(h-1) + N(h-2)
- 令G(h)=N(h)+1,则G(h)=F(h+2),F为斐波那契数列,而随着i的增大,斐波那契数列有一个性质: F i F i − 1 → 5 + 1 2 = Φ \frac{F_i}{F_{i-1}}→\frac{\sqrt{5}+1}{2}=\Phi Fi−1Fi→25+1=Φ
- 可以估算i较大时, F i ≈ Φ i 5 F_i\approx\frac{\Phi^i}{\sqrt{5}} Fi≈5Φi N h = F h + 2 − 1 = Φ h + 2 5 − 1 N_h=F_{h+2}-1=\frac{\Phi^{h+2}}{\sqrt{5}}-1 Nh=Fh+2−1=5Φh+2−1 h = l o g N h + 1 − 2 l o g Φ + 1 2 l o g 5 l o g Φ ≈ 1.44 l o g N h + C h=\frac{logN_h+1-2log\Phi+\frac{1}{2}log5}{log\Phi}\approx1.44logN_h+C h=logΦlogNh+1−2logΦ+21log5≈1.44logNh+C
- 故得证AVL的搜索效率为O(logn),在最糟糕的情况下,其搜索效率仅为完全二叉树的1.44倍,退化性能不多。
AVL的插入
AVL的查找与BST完全一致,因此无需赘述,较为困难的是AVL的插入与删除,因为必须维护AVL的平衡因子,因此涉及BF的更新与树的旋转。
再进一步之前,我们需要意识到以下几点:
- AVL是递归定义的,AVL的左右子树都是AVL树
- 上一条性质意味着,如果一个节点失衡,只会影响局部而不一定是整体。那么通过调整局部的子树,可以达到整体的平衡
- 树的旋转前后,如果不改变树的高度,那么子树平衡的同时不影响父节点的BF,说明调整完毕,否则需要继续递归向上调整
1.插入节点
插入节点与BST一致,唯一的区别在于,AVL树我们使用了三叉链和bF,需要注意parent节点的连接与bF的默认置零。
void insert(int key)
{TreeNode* cur = this->root;TreeNode* pre = cur;TreeNode* node = new TreeNode(key);//利用pre和cur找到插入的位置while (cur){pre = cur;if (key < cur->val)cur = cur->left;elsecur = cur->right;}//根节点if (this->root == nullptr){this->root = node;return;}//在左边if (key < pre->val)pre->left = node;//右边elsepre->right = node;node->parent = pre;cur = node;//.......
}
2.更新平衡因子BF
当我们插入一个新的节点时,必然会影响父节点的BF值,如果改变了父节点的高度,则会影响组父节点的BF,因此我们必须向上溯源更新BF值,更新原则如下:
- 若插入的值key < 溯源节点pre,说明新节点位于pre的左子树,左子树高度增大,pre->bF++
- 若插入的值key > 溯源节点pre,说明新节点位于pre的右子树,右子树高度增大,pre->bF–
现在我们考虑更新后的pre的平衡因子bF,从而判断是否继续向上溯源,分析如下:
- 首先明确,根据AVL的定义,更新前pre的bF可能取值为-1,0,1
- 若更新后bF为0,说明更新前为-1或1,且新节点插入了较低的子树,插入较低子树意味着pre的高度不变,无需继续溯源,插入完成,跳出循环
- 若更新后bF为-1或1,说明更新前为0,两子树高度一致,在插入新节点后,其中一颗子树高度增大,因此pre的高度发生变化,需要继续溯源,pre=pre->parent,直到根节点为止。
- 若更新后bF为-2或2,说明更新前为-1或1,且新节点插入了较高的子树,此时,pre失衡,且pre为失衡的最小子树,需要进行旋转调整,因为insert造成的失衡可以通过1次旋转完成调整,并且使pre的BF=0,因此跳出循环,进入旋转模块。
void insert(int key)
{//......//上接插入节点bool unbanlance = false;//更新bF值while (pre){//沿着搜索路径向上回溯,修改bFif (key < pre->val)++pre->bF;else--pre->bF;//平衡if (pre->bF == 0)return;//pre处失衡else if (pre->bF == 2 || pre->bF == -2){unbanlance = true;break;}//继续向上调整else{cur = pre;pre = pre->parent;}}//......
}
3.旋转调整树的结构
调整树的结构,我们可以对失衡情况进行分类,共有以下4类。
3.1 LL 右旋
如图所示:
LL代表着这样一种情况:
- 插入前,P节点的BF为1,L节点的BF为0(必然是这种情况,不可能P为1且L为1,否则P不是最先找到节点),代表着P的左子树比后子树高1,L的左右子树一致
- 插入后,L和P的左子树高度增加1,P节点的BF为2,L节点的BF为1。此时P节点失衡,我们采用右旋,下降P节点,上升L节点。
- 右转后,L和P节点的BF值都归0
//a为失衡节点,b为a的左节点
void LL(TreeNode* a, TreeNode* b)
{a->left = b->right;if (b->right != nullptr)b->right->parent = a;b->right = a;b->parent = a->parent;a->parent = b;a->bF = 0;b->bF = 0;if (b->parent==nullptr)this->root = b;else if (b->val < b->parent->val)b->parent->left = b;elseb->parent->right = b;
}
3.2 RR 左旋
如图所示:
RR对应着LL的对称情况,不必多说。
//a为失衡节点,b为a的右节点
void RR(TreeNode* a, TreeNode* b)
{bool isRoot = a->parent == nullptr;a->right = b->left;if (b->left != nullptr)b->left->parent = a;b->left = a;b->parent = a->parent;a->parent = b;a->bF = 0;b->bF = 0;if (b->parent == nullptr)this->root = b;else if (b->val < b->parent->val)b->parent->left = b;elseb->parent->right = b;
}
3.3 LR 左右双旋
如图所示:
LR对应着这一种情况:
- 插入前,与LL的情况一致。
- 插入后,L的右子树高度增加1,而P的左子树高度增加1,P节点的BF为2,L节点的BF为-1,所需要进行的调整较为复杂,但可以拆分为两步进行。
- 首先对L、LR进行一次左旋,下降L,上升LR。之后对P、LR进行一次右旋,下降P,上升LR。
- 左右双旋后,LR的BF=0,而L和P的BF则需要根据插入节点所位于LR的位置进行判断(也可根据LR之前的BF进行判断),如果插入在LR的左子树,则L->BF=0,P->BF=-1,插在LR的右子树,则L->BF=1,P->BF=0
//a为失衡节点,b为a的左节点
void LR(TreeNode* a, TreeNode* b)
{TreeNode* c = b->right;b->right = c->left;a->left = c->right;if (c->left != nullptr)c->left->parent = b;if (c->right != nullptr)c->right->parent = a;c->left = b;c->right = a;c->parent = a->parent;b->parent = c;a->parent = c;//c就是插入节点if (c->bF == 0){a->bF = 0;b->bF = 0;}//插入节点在c的左子树else if (c->bF == 1){b->bF = 0;a->bF = -1;}else{b->bF = 1;a->bF = 0;}c->bF = 0;if (c->parent == nullptr)this->root = c;else if (c->val < c->parent->val)c->parent->left = c;elsec->parent->right = c;
}
3.4 RL 右左双旋
如图所示:
RL对应着LR的对称情况,不必多说。
//a为失衡节点,b为a的右节点
void RL(TreeNode* a, TreeNode* b)
{TreeNode* c = b->left;b->left = c->right;a->right = c->left;if (c->right != nullptr)c->right->parent = b;if (c->left != nullptr)c->left->parent = a;c->left = a;c->right = b;c->parent = a->parent;a->parent = c;b->parent = c;if (c->bF == 0){a->bF = 0;b->bF = 0;}else if (c->bF == 1){a->bF = 0;b->bF = -1;}else{a->bF = 1;b->bF = 0;}c->bF = 0;if (c->parent == nullptr)this->root = c;else if (c->val < c->parent->val)c->parent->left = c;elsec->parent->right = c;
}
4 插入总结
最后我们对插入做一个总结,具体过程如下:
- 首先,从根节点出发,找到新插入节点的位置(空节点)和其父节点
- 插入节点
- 从插入节点的父节点开始,向上回溯更新BF
- 若是更新后的BF=1或-1,则继续更新,直到根节点为止;若是更新后的BF=0,则插入结束,返回;若是更新后的BF=2或-2,则找到了最小的失衡AVL子树,跳出循环,修复该子树。
- 若是失衡,则根据失衡节点a和插入节点所在分支的子节点b的BF值,判断是LL/RR/LR/RL中哪种情况,并进行相应的旋转操作。
完整代码如下:
//插入
void insert(int key)
{TreeNode* cur = this->root;TreeNode* pre = cur;TreeNode* node = new TreeNode(key);//利用pre和cur找到插入的位置while (cur){pre = cur;if (key < cur->val)cur = cur->left;elsecur = cur->right;}//根节点if (this->root == nullptr){this->root = node;return;}//在左边if (key < pre->val)pre->left = node;//右边elsepre->right = node;node->parent = pre;cur = node;bool unbanlance = false;//更新bF值while (pre){//沿着搜索路径向上回溯,修改bFif (key < pre->val)++pre->bF;else--pre->bF;//平衡if (pre->bF == 0)return;//pre处失衡else if (pre->bF == 2 || pre->bF == -2){unbanlance = true;break;}//继续向上调整else{cur = pre;pre = pre->parent;}}//失衡状态需要调整if (unbanlance){//LL型if (pre->bF == 2 && cur->bF == 1)LL(pre, cur);else if (pre->bF == 2 && cur->bF == -1)LR(pre, cur);else if (pre->bF == -2 && cur->bF == -1)RR(pre, cur);elseRL(pre, cur);}return;
}
AVL的删除
相比于插入,AVL的删除实际上可能更加困难,正如BST的删除也比插入更难。
与BST一致,我们依然是从叶节点、单边节点和双边节点开始考虑。
1.寻找删除节点
我们删除节点的流程应为:找到并记录删除节点->更新BF值->调整树结构->实际删除节点。
- 无删除节点,返回
- 叶节点,记录下该节点和父节点
- 单边节点,记录下该节点和父节点
- 双边节点,采用替换删除法,采用前驱(左子树最大值)或后继(右子树最小值)替换该删除节点的值,实际删除节点为前驱或后继节点,本程序采用后继,记录下后继节点和父节点。
- 删除节点是叶节点或单边节点,同时是根节点的情况,需要特殊处理。(双边节点实际上删的是后继节点,所以不需要单独处理)
void remove(int key)
{TreeNode* cur = this->root;TreeNode* pre = nullptr;TreeNode* deleteNode = nullptr;TreeNode* deleteParent = nullptr;while (cur){if (key > cur->val){pre = cur;cur = cur->right;}else if (key < cur->val){pre = cur;cur = cur->left;}//找到了需要删除的节点else{//需要删除节点的左子树为空if (cur->left == nullptr){//若是根节点,将右子树作为新的根节点即可//根节点没有父节点,无需更新bFif (cur->parent == nullptr){root = cur->right;if (root)root->parent = nullptr;delete(cur);return;}else{//记录信息deleteNode = cur;deleteParent = pre;}}else if (cur->right == nullptr){if (cur->parent == nullptr){root = cur->left;if (root)root->parent = nullptr;delete(cur);return;}else{deleteNode = cur;deleteParent = pre;}}else{//左右子树都非空,进行替换,并且更新需要删除的位置//利用rightMin进行更新TreeNode* minRight = cur->right;while (minRight->left)minRight = minRight->left;//替换cur->val = minRight->val;//标记删除节点deleteNode = minRight;deleteParent = minRight->parent;}break;}}//没有需要删除的节点if (deleteParent == nullptr)return;//.......
}
2.更新平衡因子BF + 旋转
不同于插入,在删除之中,旋转可能会改变树的高度,因此更新BF和旋转必须在一个循环中反复进行,不能拆分进行。
毫无疑问,我们依然需要确立更新原则,更新原则如下:
- 若删除的节点 < 溯源节点deleteParent,说明删除节点位于deleteParent的左子树,左子树高度减小,deleteParent->bF–
- 若删除的节点 > 溯源节点deleteParent,说明删除节点位于deleteParent的右子树,右子树高度增孝,deleteParent->bF++
现在我们考虑更新后的deleteParent的平衡因子bF,从而判断是否继续向上溯源,分析如下:
- 依然明确,根据AVL的定义,更新前deleteParent的bF可能取值为-1,0,1
- 若更新后bF为0,说明更新前为-1或1,删除了较高子树的节点,继续向上回溯。
- 若更新后bF为-1或1,说明更新前为0,两子树高度一致,删除其中一棵子树的节点,树的高度没有发生变化,至此插入结束。
- 若更新后bF为-2或2,说明更新前为-1或1,且删除了较低子树的节点,此时,deleteParent失衡,需要进行旋转调整,旋转调整分为6种情况,其中4种情况会改变树的高度,需要继续向上回溯。
以下为失衡时的6种情况,以及对应的处理方法:
- 当deleteParent的平衡因子BF为2,deleteParent的左孩子平衡因子为1时,即降低了R节点的树高,与插入时的LL情况一致,采用右旋,旋转前的子树路径为P->L->L的左子树,高度为1+1+h,旋转后的子树路径为L->L的左子树,高度为1+h,右子树为L->P->(L右子树h-1)或(P右子树h-1),高度由h+2→h+1,必须继续回溯。
- 当deleteParent的平衡因子BF为2,deleteParent的左孩子平衡因子为-1时,即降低了R节点的树高,与插入时的LR情况一致,采用左右双旋,同上进行分析,高度h+2→h+1,继续回溯。
- 当deleteParent的平衡因子BF为2,deleteParent的左孩子平衡因子为0时,此时情况较为特殊,降低了R的树高,但是L的两个子树高度一致,这是插入中没有的情况,我们采用右旋+改变平衡因子调整方法的方法进行,右旋后,将L->BF=-1,P->BF=1,旋转前后的高度h+2→h+1,高度没有变化,不需要继续回溯
- 当deleteParent的平衡因子BF为-2,deleteParent的左孩子平衡因子为-1时,第1种情况的对称情况,左旋,继续回溯。
- 当deleteParent的平衡因子BF为-2,deleteParent的左孩子平衡因子为1时,第2种情况的对称情况,右左双旋,继续回溯
- 当deleteParent的平衡因子BF为-2,deleteParent的左孩子平衡因子为0时,第3种情况的对称情况,左旋+改变平衡因子调整方法,将R->BF=1,P->BF=-1,不需要继续回溯。
void remove(int key)
{//.....//上接寻找删除节点//备份TreeNode* delP = deleteParent;TreeNode* del = deleteNode;//更新bFwhile (deleteParent){//删除左子树if (deleteNode->val < deleteParent->val)--deleteParent->bF;else++deleteParent->bF;//根据bF进一步判断//bF=0,说明原来为-1 或者 1,此时改变了树的高度,需要继续向上更新if (deleteParent->bF == 0){deleteNode = deleteParent;deleteParent = deleteParent->parent;}//bF=1 / -1,说明原来为0,此时没有修改树的高度(高度由最高的子树决定),不需要继续更新else if (deleteParent->bF == 1 || deleteParent->bF == -1){break;}//bF=2 / -2,失衡,需要进行旋转else{//左边子树高if (deleteParent->bF == 2){//LL情况if (deleteParent->left->bF == 1)LL(deleteParent, deleteParent->left);//LRelse if (deleteParent->left->bF == -1)LR(deleteParent, deleteParent->left);else{//由于右子树的降低而导致的失衡,左节点的两个子树高度一致//可以采用LL进行处理,但需要重新调整bFLL(deleteParent, deleteParent->left);//调整deleteNode和左子节点如今的位置deleteParent = deleteParent->parent;//旋转前,左子树=1节点+2个节点的子树AB(高h) 高h+1;右子树=1个子树C(高h-1) 高h-1//旋转后,左子树=子树A 高h,右子树=原来根节点 + 左子树B(高h)+右子树C(高h-1) 高h+1//因此,新的根节点左子树低于右子树,右节点的子树则是左子树高于右子树deleteParent->bF = -1;deleteNode->right->bF = 1;//此时,树的高度没有发生变化,不需要继续向上更新,故breakbreak;}}else{//RRif (deleteParent->right->bF == -1)RR(deleteParent, deleteParent->right);//RLelse if (deleteParent->right->bF == 1)RL(deleteParent, deleteParent->right);else{RR(deleteParent, deleteParent->right);deleteParent = deleteParent->parent;deleteParent->bF = 1;deleteParent->left->bF = -1;break;}}//旋转会调整树的高度,需要继续更新(不需要更新的情况已经break了)deleteNode = deleteParent;deleteParent = deleteParent->parent;}}//......
}
3.实际删除节点
利用备份好的删除节点信息,考虑单边节点和删除节点所位于的子树情况进行删除。
void remove(int key)
{//.....//上接bf调整和旋转//删除节点(必然有一颗子树为空)//删除节点的左子树为空if (del->left == nullptr){//删除节点位于左子树if (del->val < delP->val)delP->left = del->right;elsedelP->right = del->right;if (del->right != nullptr)del->right->parent = delP;}//右子树为空else{if (del->val < delP->val)delP->left = del->left;elsedelP->right = del->left;//此时delteNode->left必然不为nullptr(这种情况已经讨论过)del->left->parent = delP;}delete(del);return;
}
4.删除总结
相比于插入,删除需要注意的情况更多,且存在旋转改变高度,上层父节点也需要旋转的可能。
在此就不再列删除流程,而是记录一些关键点:
- 对于删除的节点种类的选择:叶节点、单边节点、双边节点,双边采用替换删除法转为叶节点或单边节点
- 更新BF和旋转树需要同时在循环内进行,循环停止条件为不改变树高度或到达根节点
- 不改变树高度分为删除本身不改变和旋转后恢复删除前高度两种情况,后者只在父节点的BF=2或-2,且子节点BF=0时出现
总体代码如下:
void remove(int key)
{TreeNode* cur = this->root;TreeNode* pre = nullptr;TreeNode* deleteNode = nullptr;TreeNode* deleteParent = nullptr;while (cur){if (key > cur->val){pre = cur;cur = cur->right;}else if (key < cur->val){pre = cur;cur = cur->left;}//找到了需要删除的节点else{//需要删除节点的左子树为空if (cur->left == nullptr){//若是根节点,将右子树作为新的根节点即可//根节点没有父节点,无需更新bFif (cur->parent == nullptr){root = cur->right;if (root)root->parent = nullptr;delete(cur);return;}else{//记录信息deleteNode = cur;deleteParent = pre;}}else if (cur->right == nullptr){if (cur->parent == nullptr){root = cur->left;if (root)root->parent = nullptr;delete(cur);return;}else{deleteNode = cur;deleteParent = pre;}}else{//左右子树都非空,进行替换,并且更新需要删除的位置//利用rightMin进行更新TreeNode* minRight = cur->right;while (minRight->left)minRight = minRight->left;//替换cur->val = minRight->val;//标记删除节点deleteNode = minRight;deleteParent = minRight->parent;}break;}}//没有需要删除的节点if (deleteParent == nullptr)return;//备份TreeNode* delP = deleteParent;TreeNode* del = deleteNode;//更新bFwhile (deleteParent){//删除左子树if (deleteNode->val < deleteParent->val)--deleteParent->bF;else++deleteParent->bF;//根据bF进一步判断//bF=0,说明原来为-1 或者 1,此时改变了树的高度,需要继续向上更新if (deleteParent->bF == 0){deleteNode = deleteParent;deleteParent = deleteParent->parent;}//bF=1 / -1,说明原来为0,此时没有修改树的高度(高度由最高的子树决定),不需要继续更新else if (deleteParent->bF == 1 || deleteParent->bF == -1){break;}//bF=2 / -2,失衡,需要进行旋转else{//左边子树高if (deleteParent->bF == 2){//LL情况if (deleteParent->left->bF == 1)LL(deleteParent, deleteParent->left);//LRelse if (deleteParent->left->bF == -1)LR(deleteParent, deleteParent->left);else{//由于右子树的降低而导致的失衡,左节点的两个子树高度一致//可以采用LL进行处理,但需要重新调整bFLL(deleteParent, deleteParent->left);//调整deleteNode和左子节点如今的位置deleteParent = deleteParent->parent;//旋转前,左子树=1节点+2个节点的子树AB(高h) 高h+1;右子树=1个子树C(高h-1) 高h-1//旋转后,左子树=子树A 高h,右子树=原来根节点 + 左子树B(高h)+右子树C(高h-1) 高h+1//因此,新的根节点左子树低于右子树,右节点的子树则是左子树高于右子树deleteParent->bF = -1;deleteNode->right->bF = 1;//此时,树的高度没有发生变化,不需要继续向上更新,故breakbreak;}}else{//RRif (deleteParent->right->bF == -1)RR(deleteParent, deleteParent->right);//RLelse if (deleteParent->right->bF == 1)RL(deleteParent, deleteParent->right);else{RR(deleteParent, deleteParent->right);deleteParent = deleteParent->parent;deleteParent->bF = 1;deleteParent->left->bF = -1;break;}}//旋转会调整树的高度,需要继续更新(不需要更新的情况已经break了)deleteNode = deleteParent;deleteParent = deleteParent->parent;}}//删除节点(必然有一颗子树为空)//删除节点的左子树为空if (del->left == nullptr){//删除节点位于左子树if (del->val < delP->val)delP->left = del->right;elsedelP->right = del->right;if (del->right != nullptr)del->right->parent = delP;}//右子树为空else{if (del->val < delP->val)delP->left = del->left;elsedelP->right = del->left;//此时delteNode->left必然不为nullptr(这种情况已经讨论过)del->left->parent = delP;}delete(del);return;
}
总结
总算把AVL树的博客写完了,我发现大量的博客确实缺少了对于AVL删除的叙述,有些可惜。
之后的红黑树、B树、B+树、哈夫曼树,估计不会自己实现,而是记录一下思路和细节,也没有必要再费劲地去处理红黑树N多种情况。
——2023.5.17
相关文章:

[日记]LeetCode算法·二十五——二叉树⑤ AVL树(插入+删除)附代码实现
本章的代码实现基于上一篇BST与优先队列的基类进行平衡二叉树,即AVL树。 文章目录 AVL的概念AVL查询效率AVL的插入1.插入节点2.更新平衡因子BF3.旋转调整树的结构3.1 LL 右旋3.2 RR 左旋3.3 LR 左右双旋3.4 RL 右左双旋 4 插入总结 AVL的删除1.寻找删除节点2.更新平…...

flink-1.13.6 例子
-------------------------------------------------------------- flink版本: flink-1.13.6 [rootmaster bin]# pip3 list | grep flink WARNING: Ignoring invalid distribution -andas (/usr/local/python38/lib/python3.8/site-packages) apache-flink 1.13.0 a…...

Go语音基于zap的日志封装
zap日志封装 Zap是一个高性能、结构化日志库,专为Go语言设计。它由Uber开源,并且在Go社区中非常受欢迎。它的设计目标是提供一个简单易用、高效稳定、灵活可扩展的日志系统。 以下是Zap的一些主要特点: 1.高性能:Zap的性能非常出…...

可持续能源技术具有改变世界的潜力,并且已经在多个方面展现出积极的影响。
可持续能源技术的发展在当今全球面临的气候变化和能源安全挑战中扮演着至关重要的角色。我认为可持续能源技术具有改变世界的潜力,并且已经在多个方面展现出积极的影响。以下是我对此的观点: 1,可持续能源技术有助于减少对化石燃料的依赖 化…...
Java常用工具之StringUtils类
目录 一、字符串判空二、分隔字符串三、判断是否为纯数字四、将集合拼接成字符串五、其他方法 字符串(String)在我们的日常工作中,用得非常非常非常多。 在我们的代码中经常需要对字符串判空,截取字符串、转换大小写、分隔字符串、…...

MyBatis-plus的批量插入方式对比分析
MyBatis-plus的批量插入方式对比分析 【摘要】Mybatis批量插入一直是开发者重点关注的问题,本文列举了Mybatis的五种插入方式进行对比分析,验证了五种批量插入的方式的优先级。 1 准备工作 1.1 新建spring项目 略。 1.2 导入pom.xml依赖 <depende…...

【系分论文】论软件开发模型及应用
目录 论题论题介绍论文要点理论素材准备范文摘要正文 论文补充知识 论题 论软件开发模型及应用 论题介绍 软件开发模型( Software Development Model)是指软件开发全部过程、活动和任务的结构框架。软件开发过程包括需求、设计、编码和测试等阶段&…...
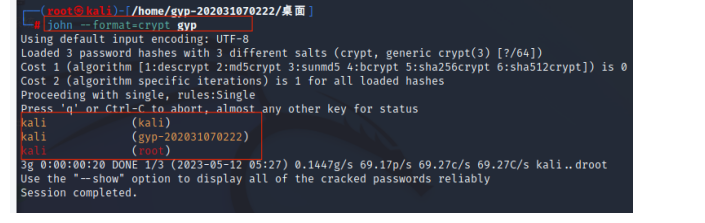
渗透测试--5.3.使用john破解密码
前言 由于Linux是Internet最流行的服务器操作系统,因此它的安全性备受关注。这种安全主要靠口令实现。 Linux使用一个单向函数crypt()来加密用户口令。单向函数crypt()从数学原理上保证了从加密的密文得到加密前的明…...

Go中的变量类型
Go中的变量类型 1.为什么要使用变量 变量其实指定的是一段内存地址,根据这个内存地址可以找到我们需要找到的东西。 2.变量类型 变量的功能就是用来存储数据的,根据不同的数据类型可以存储不同的数据。常见的变量的类型 整型、浮点型、布尔型等。变…...

基于STM32的NRF24L01 2.4G通讯模块的驱动实验(HAL库)
前言:本文为手把手教学NRF24L01 2.4G通讯模块的驱动实验,本教程的 MCU 采用STM32F103ZET6与STM32F103C8T6,彼此进行互相通讯。通过 CubeMX 软件配置 SPI 协议驱动NRF24L01 2.4G通讯模块(HAL库)。NRF24L01 2.4G是嵌入式…...
DJ5-3 多路访问链路和协议
目录 一、网络链路 二、广播信道要解决问题 三、多路访问协议 1、基本介绍 2、多路访问协议的类型(3) 四、信道划分协议 1、时分多路访问 TDMA 2、频分多路访问 FDMA 3、码分多路访问 CDMA(略) 五、随机访问协议 1、纯…...

技术领导力?
作品集(Portfolio)会比简历(Resume)更有参考意义。 怎么才算有技术领导力? 1) 能够发现问题,并能够提供解决问题的思路和方案,并能比较方案的优缺点。 2) 能用更简洁有效的方式解决问题。 3…...
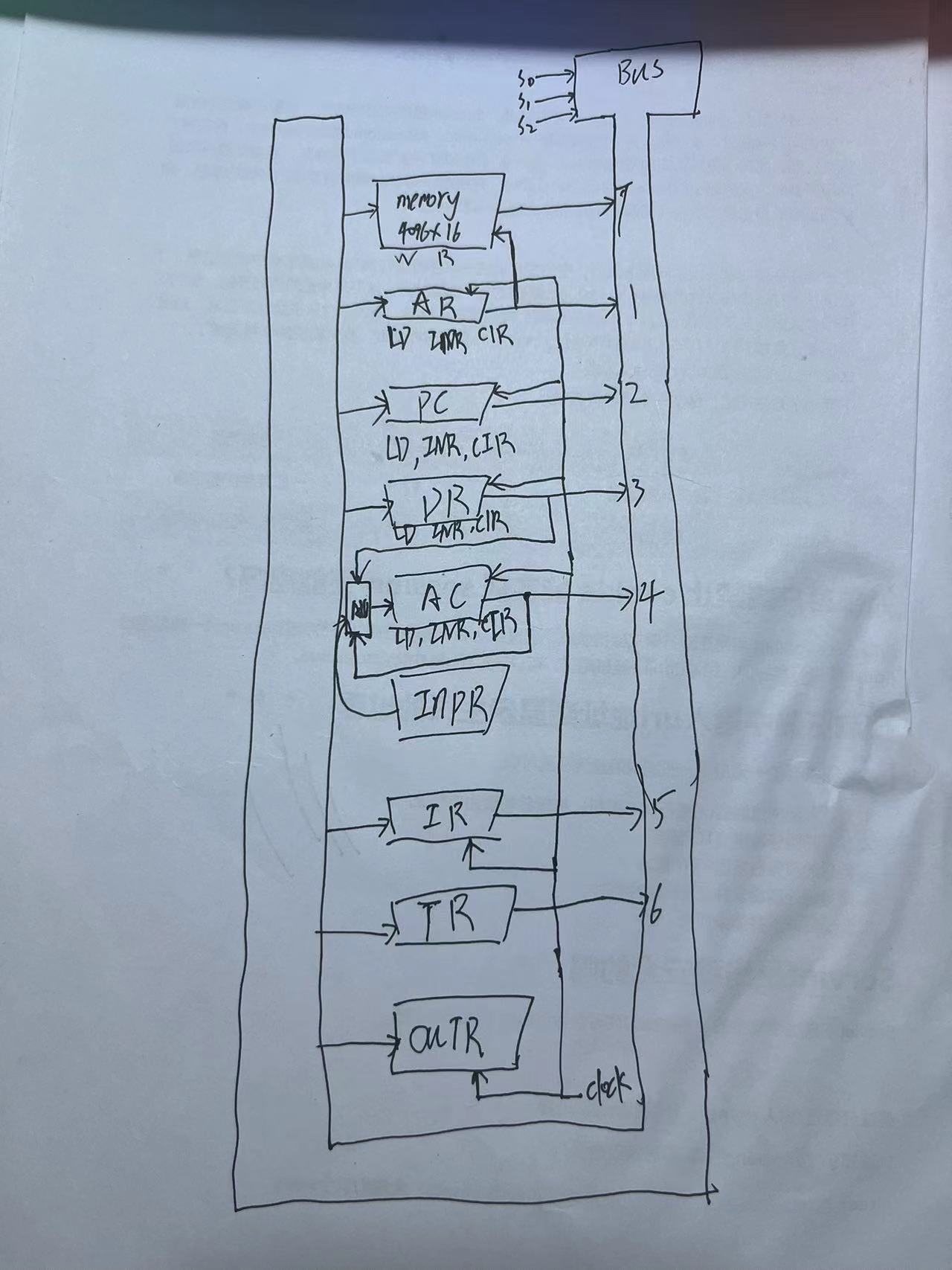
计算机的基本工作原理
参考资料: L-1.6: Common Bus system| How basic computer works - YouTube 准备好内存单元、不同类型的寄存器,内存和寄存器、寄存器和寄存器之间都是通过总线连接(假设是直接把数据总线、控制总线、地址总线变成一条总线)。 使用多路复用器实现的总线&…...
【论文简述】Cross-Attentional Flow Transformer for Robust Optical Flow(CVPR 2022)
一、论文简述 1. 第一作者:Xiuchao Sui、Shaohua Li 2. 发表年份:2021 3. 发表期刊:arxiv 4. 关键词:光流、Transformer、自注意力、交叉注意力、相关体 5. 探索动机:由于卷积的局部性和刚性权重,有限…...

【JAVA】Java中方法的使用,理解方法重载和递归
目录 1.方法的概念及使用 1.1什么是方法 1.2方法的定义 1.3方法调用的执行过程 1.4实参和形参 2.方法重载 2.1为什么需要使用方法重载 2.2什么是方法重载 3.递归 3.1什么是递归 3.2递归执行的过程 3.3递归的使用 1.方法的概念及使用 1.1什么是方法 方法就是一个代…...

高级网络计算模式复习
P2P 对等网络(Peer-to-Peer Networks)是分布式系统和计算机网络相结合的产物,在应用领域和学术界获得了广泛的重视和成功,被称为“改变Internet的一代网络技术”。 peer指网络结点,在行为上是自由的——任意加入、退…...

【笔试强训选择题】Day15.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!! 文章目录 前言 一、…...
)
图论专题(一)
图论专题(一) 参考文献 BFS和DFS的直观解释 https://blog.csdn.net/c406495762/article/details/117307841Leetcode岛屿问题系列分析 https://blog.csdn.net/qq_39144436/article/details/124173504多源广度优先 https://blog.csdn.net/peko1/article/details/121989497拓扑排…...

新星计划2023【网络应用领域基础】————————Day4
常见的网络基础介绍 前言 我们学习了一些基础的网络协议,以及子网掩码和vlan,同时也做了个简单的单臂路由实验 这篇文章我将仔细的讲解单臂路由的应用和交换机二层接口类型,以及wireshark的教程。 一,交换机二层接口 交换机的二…...

[CTF/网络安全] 攻防世界 view_source 解题详析
[CTF/网络安全] 攻防世界 view_source 解题详析 查看页面源代码方式归类总结 题目描述:X老师让小宁同学查看一个网页的源代码,但小宁同学发现鼠标右键好像不管用了。 查看页面源代码方式归类 单击鼠标右键,点击查看页面源代码: …...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
