这个 归并排序详解过程 我能吹一辈子!!!
文章目录
- 归并排序概念
- 归并排序算法思路
- 归并排序递归实现
- 归并排序非递归实现
归并排序概念
1945年,约翰·冯·诺依曼(John von Neumann)发明了归并排序,这是典型的分治算法的应用。
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
归并排序算法思路
归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成两个子数组的过程。另一个是治,它将两个有序数组合并成一个更大的有序数组。
1> 将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
2> 将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。

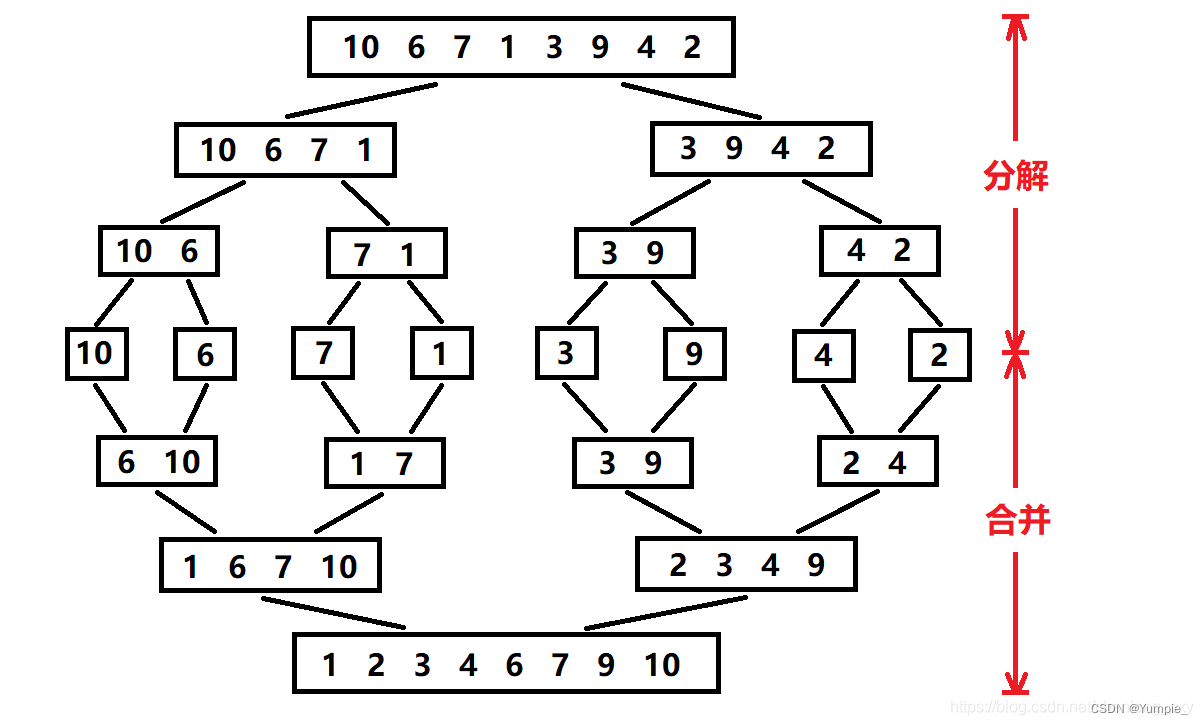
相信大家都知道如何将两个有序序列合为一个有序序列吧:

那么如何得到有序的子序列呢?当序列分解到只有一个元素或是没有元素时,就可以认为是有序了,这时分解就结束了,开始合并:
归并排序递归实现
归并排序,从其思想上看就很适合使用递归来实现,并且用递归实现也比较简单。其间我们需要申请一个与待排序列大小相同的数组用于合并过程两个有序的子序列,合并完毕后再将数据拷贝回原数组。
代码示例:
//归并排序(子函数)
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)//归并结束条件:当只有一个数据或是序列不存在时,不需要再分解{return;}int mid = left + (right - left) / 2;//中间下标_MergeSort(a, left, mid, tmp);//对左序列进行归并_MergeSort(a, mid + 1, right, tmp);//对右序列进行归并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;//将两段子区间进行归并,归并结果放在tmp中int i = left;while (begin1 <= end1&&begin2 <= end2){//将较小的数据优先放入tmpif (a[begin1] < a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];//归并完后,拷贝回原数组int j = 0;for (j = left; j <= right; j++)a[j] = tmp[j];
}
//归并排序(主体函数)
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与原数组大小相同的空间if (tmp == NULL){printf("malloc fail\n");exit(-1);}_MergeSort(a, 0, n - 1, tmp);//归并排序free(tmp);//释放空间
}时间复杂度:O(N*logN) 空间复杂度:O(N)
归并排序非递归实现
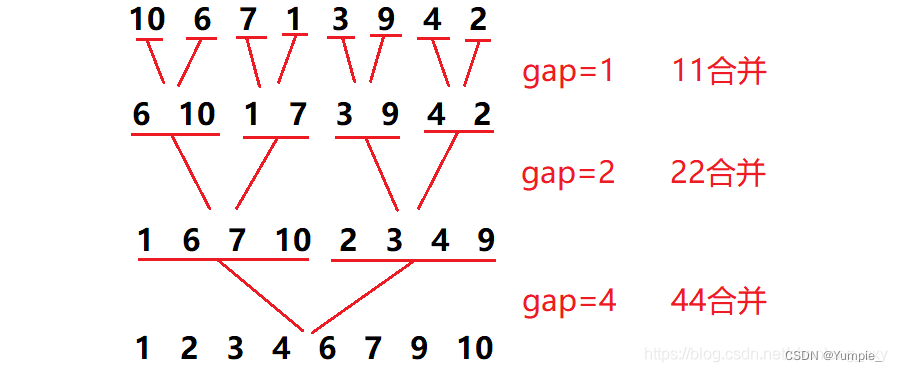
归并排序的非递归算法并不需要借助栈来完成,我们只需要控制每次参与合并的元素个数即可,最终便能使序列变为有序:
当然,以上例子是一个待排序列长度比较特殊的例子,我们若是想写出一个广泛适用的程序,必定需要考虑到某些极端情况:
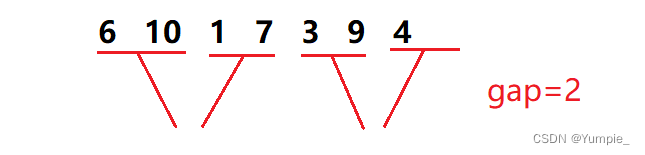
情况一:
当最后一个小组进行合并时,第二个小区间存在,但是该区间元素个数不够gap个,这时我们需要在合并序列时,对第二个小区间的边界进行控制。
情况二:
当最后一个小组进行合并时,第二个小区间不存在,此时便不需要对该小组进行合并。
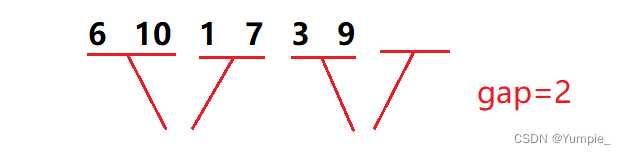
情况三:
当最后一个小组进行合并时,第二个小区间不存在,并且第一个小区间的元素个数不够gap个,此时也不需要对该小组进行合并。(可与情况二归为一类)
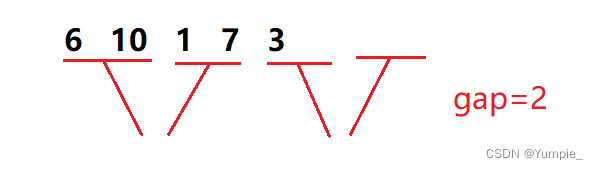
只要把控好这三种特殊情况,写出归并排序的非递归算法便轻而易举了。
代码示例:
//归并排序(子函数)
void _MergeSortNonR(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{int j = begin1;//将两段子区间进行归并,归并结果放在tmp中int i = begin1;while (begin1 <= end1&&begin2 <= end2){//将较小的数据优先放入tmpif (a[begin1] < a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];//归并完后,拷贝回原数组for (; j <= end2; j++)a[j] = tmp[j];
}
//归并排序(主体函数)
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与待排序列大小相同的空间,用于辅助合并序列if (tmp == NULL){printf("malloc fail\n");exit(-1);}int gap = 1;//需合并的子序列中元素的个数while (gap < n){int i = 0;for (i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (begin2 >= n)//最后一组的第二个小区间不存在或是第一个小区间不够gap个,此时不需要对该小组进行合并break;if (end2 >= n)//最后一组的第二个小区间不够gap个,则第二个小区间的后界变为数组的后界end2 = n - 1;_MergeSortNonR(a, tmp, begin1, end1, begin2, end2);//合并两个有序序列}gap = 2 * gap;//下一趟需合并的子序列中元素的个数翻倍}free(tmp);//释放空间
}时间复杂度:O(N*logN) 空间复杂度:O ( N )
相关文章:
这个 归并排序详解过程 我能吹一辈子!!!
文章目录 归并排序概念归并排序算法思路归并排序递归实现归并排序非递归实现 归并排序概念 1945年,约翰冯诺依曼(John von Neumann)发明了归并排序,这是典型的分治算法的应用。 归并排序(Merge sort)是建立…...

docker版jxTMS使用指南:自动生成代码
本文讲解4.0版jxTMS的自动生成代码功能, 整个系列的文章请查看:docker版jxTMS使用指南:4.0版升级内容 docker版本的使用,请参考:docker版jxTMS使用指南 任何一个管理系统都需要对管理对象进行管理,包括最…...

聚观早报 | 小冰启动GPT克隆人计划;ofo创始人在美创业改做咖啡
今日要闻:小冰启动“GPT克隆人计划”;ofo创始人在美创业改做咖啡;OpenAI正准备新的开源AI模型;青年失业率首破20%创新高;微软收购动视暴雪获批 小冰启动“GPT克隆人计划” 5 月 16 日,小冰公司…...
面试造航母,入职拧螺丝,工资离了个大谱...
有粉丝跟我吐槽说:金三银四去面试软件测试岗,真的是面试造航母,入职拧螺丝,工资还低 这种现象很正常,因为找一个测试员,当然希望他能做的业务越多越好,最好像机器猫一样,啥事儿都能…...

Python+selenium自动化元素定位防踩坑
在自动化UI测试过程中常常会在元素定位阶段就踩坑,碰到困扰已久的问题。 以下是个人整理元素定位报错原因和解决方法。 踩坑一:StaleElementReferenceException selenium.common.exceptions.StaleElementReferenceException: Message: stale element re…...

【计算机组成原理】实验一
文章目录 实验一 数据传送实验1. 实验目的2. 实验仪器3. 原理概述4. 实验内容步骤4.1 手动实验环境的建立4.2 手控传送实验 5. 实验结论及问题讨论 实验一 数据传送实验 1. 实验目的 2. 实验仪器 3. 原理概述 4. 实验内容步骤 4.1 手动实验环境的建立 1)初始待令状态 上电或…...

前端022_广告模块_修改功能
广告模块_修改功能 1、需求分析2、Mock添加查询数据3、Mock修改数据4、Api调用回显数据5、提交修改后的数据6、效果1、需求分析 需求分析 当点击 编辑 按钮后,弹出编辑窗口,并查询出分类相关信息进行渲染。修改后点击 确定 提交修改后的数据。 2、Mock添加查询数据 请求URL…...
:C++的编译及库文件的生成与链接)
makefile 学习(3):C++的编译及库文件的生成与链接
1. 介绍 C语言的相关后缀 .a 文件是一个静态库文件.c,.c ,.cp,.cpp,.cc,.cxx 这几种后缀都可以表示c的源文件.h ,.hpp c语言的头文件.i 是c预处理文件.o 目标文件.s汇编语言的文件.so 动态库或者共享库或者称为运行时库 2. C编译 2.1 预处理 g -E helloworld.cpp # 虽…...
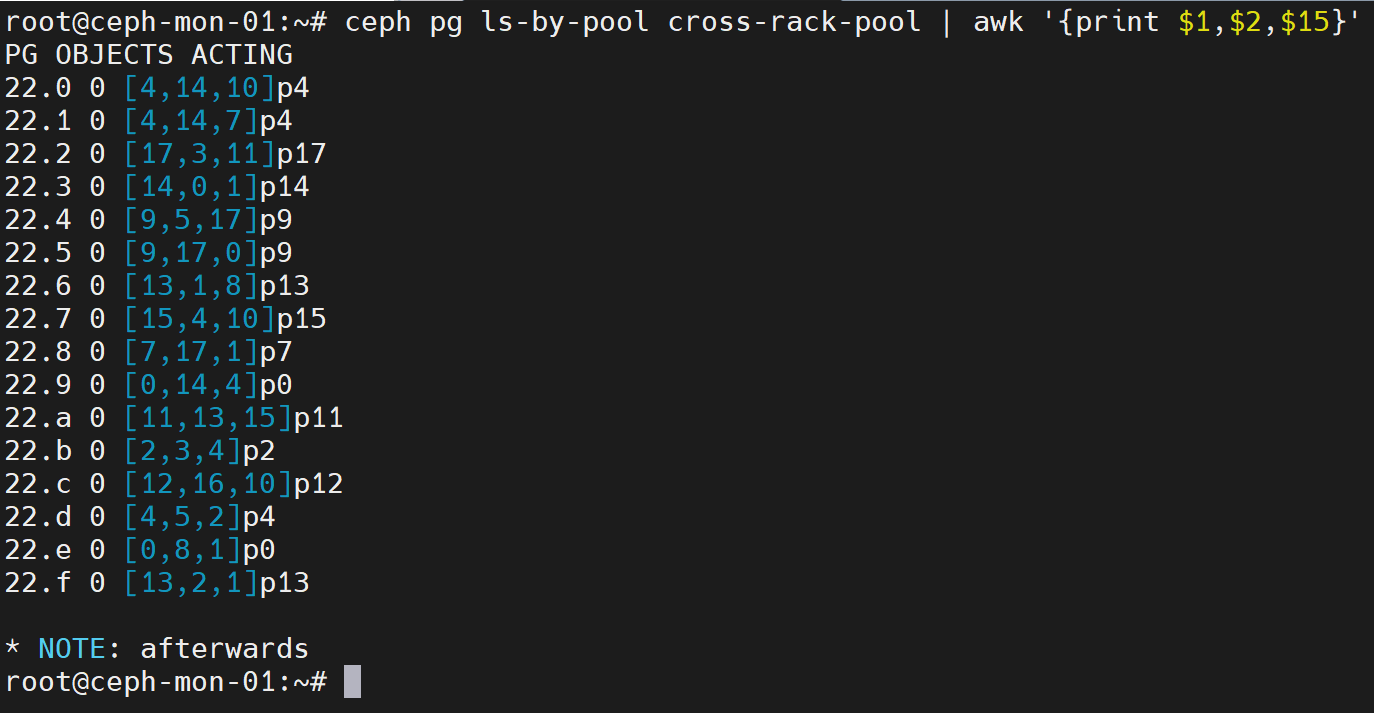
Ceph crush运行图
Crush map介绍 ceph集群中由monitor负责维护的运行图包括: Monitor map:监视器运行图osd map:osd运行图PG map:PG运行图Crush map:crush运行图Mds map:mds运行图 crush map是ceph集群物理拓扑的抽象&…...

【分布族谱】泊松分布和二项分布、正态分布的关系
文章目录 泊松分布和二项分布的关系和正态分布的关系 泊松分布 如果在有限时间 ( 0 , 1 ) (0,1) (0,1)内进行 n n n次伯努利实验,那么每次伯努利实验所占用的时间为 1 n \frac{1}{n} n1,按照自然规律,一件事情肯定是时间越长越容易发生&am…...

关于QTreeWidget的setData函数
当使用 Q T r e e W i d g e t I t e m QTreeWidgetItem QTreeWidgetItem 的 s e t D a t a setData setData 方法时,需要传递三个参数,分别是列索引、角色和数据。 列索引:表示要设置数据的列的索引。 Q T r e e W i d g e t I t e m QTre…...
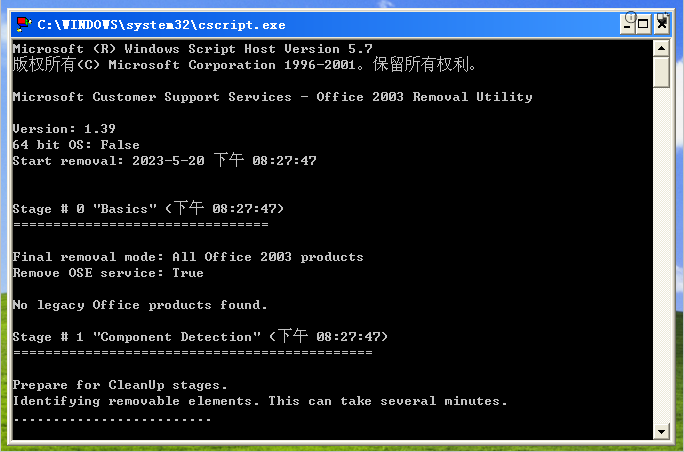
Microsoft Office 2003的安装
哈喽,大家好。今天一起学习的是office2003的安装,这个老版本的office可是XP操作系统的老搭档了,有兴趣的小伙伴也可以来一起试试手。 一、测试演示参数 演示操作系统:Windows XP 不建议win7及以上操作系统使用 系统类型ÿ…...

使用Spring Boot和Spring Cloud实现多租户架构:支持应用多租户部署和管理
使用Spring Boot和Spring Cloud实现多租户架构:支持应用多租户部署和管理 一、概述1 什么是多租户架构?2 多租户架构的优势3 实现多租户架构的技术选择 二、设计思路1 架构选型1.1 Spring Boot1.2 Spring Cloud 2 数据库设计3 应用多租户部署3.1 应用隔离…...

智聚北京!相约全球人力资源数智化峰会
人力资源是推动经济社会发展的第一资源。作为我国经济压舱石的中央企业在对标世界一流企业和管理提升方面的持续创新,各行业领军企业围绕组织变革、管理升级、全球化发展走深走实。人力资源管理正从传统职能管理与管控,向紧贴业务战略实现、组织边界和人…...

工业缺陷检测数据及代码(附代码)
介绍 目前,基于机器视觉的表面缺陷检测设备已广泛取代人工视觉检测,在包括3C、汽车、家电、机械制造、半导体与电子、化工、制药、航空航天、轻工等多个行业领域得到应用。传统的基于机器视觉的表面缺陷检测方法通常采用常规图像处理算法或人工设计的特征加分类器。一般而言…...
CentOS 安装MongoDB 6.0
一、安装依赖 yum install libcurl openssl xz-libs 二、下载安装包 安装包下载地址https://www.mongodb.com/try/download/community这里我选择的是 选择RedHat / CentOS 7.0平台的原因是我的操作系统使用的是CentOS 7.0的,需要下载与操作系统匹配的安装包 三、…...
美团面试,被拷打了一小时....
刚从美团走出来,被拷打了一小时…越想越觉得可惜,回想面试经过,好好总结了几个点,发现面试没过的主要原因是在几个关键的问题没有给到面试官想要的答案。从而失去了这次宝贵的机会。 根据你的工作经历,说说你对质量保证…...

017+C语言中函数栈帧的创建与销毁(VS2022环境)
0.前言 您好,这里是limou3434的一篇个人博文,感兴趣的话您也可以看看我的其他文章。本次我将和您一起学习在C语言中函数栈帧的概念。 1.学习函数栈帧的意义 局部变量是怎么穿创建的?为什么局部变量的值是随机的函数是怎么传参的࿱…...

马斯克们叫停 GPT-5,更像是场行为艺术
目录 01 联名信说了什么? 02 发起方是谁? 03 谁签署了联名信? 04 联名信有哪些问题?三巨头的另外两位 Sam Altman 的表态 其他值得关注的署名者 比如马斯克。 另一个位于前列的署名者是 Stability AI 的创始人 Emad Most…...

事务基础知识
第13章 事务基础知识 1. 数据库事务概述 1.1 基本概念 **事务:**一组逻辑操作单元,使数据从一种状态变换到另一种状态。 **事务处理的原则:**保证所有事务都作为一个工作单元来执行,即使出现了故障,都不能改变这种…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
