【分布族谱】泊松分布和二项分布、正态分布的关系
文章目录
- 泊松分布
- 和二项分布的关系
- 和正态分布的关系
泊松分布
如果在有限时间 ( 0 , 1 ) (0,1) (0,1)内进行 n n n次伯努利实验,那么每次伯努利实验所占用的时间为 1 n \frac{1}{n} n1,按照自然规律,一件事情肯定是时间越长越容易发生,假定事件发生的概率与 1 n \frac{1}{n} n1成正比,记作 λ n \frac\lambda n nλ,则二项分布变为
P { X = k } = ( n k ) ( λ n ) k ( 1 − λ n ) n − k P\{X=k\}=\binom{n}{k}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k} P{X=k}=(kn)(nλ)k(1−nλ)n−k
如果这个时间差 1 n \frac1n n1非常小,以至于事件变得近似连续,则有
lim n → ∞ P { X = k } = lim n → ∞ ( n k ) ( λ n ) k ( 1 − λ n ) n − k \lim_{n\to\infty} P\{X=k\}=\lim_{n\to\infty}\binom{n}{k}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k} n→∞limP{X=k}=n→∞lim(kn)(nλ)k(1−nλ)n−k
其中
lim n → ∞ ( n k ) ( λ n ) k = λ k k ! \lim_{n\to\infty}\binom{n}{k}(\frac{\lambda}{n})^k=\frac{\lambda^k}{k!} n→∞lim(kn)(nλ)k=k!λk
而后面有一项更是传说中的重要极限
lim n → ∞ ( 1 − λ n ) n = e − λ \lim_{n\to\infty}(1-\frac{\lambda}{n})^n=e^{-\lambda} n→∞lim(1−nλ)n=e−λ
综上就得到了一个新的分布
P ( x = k ) = e − λ λ k k ! P(x=k)=\frac{e^{-\lambda}\lambda^k}{k!} P(x=k)=k!e−λλk
此即泊松分布,表示某个随机事件在连续时间内发生的概率,其中 λ n \frac\lambda n nλ表示单位时间内某件事发生的概率。
和二项分布的关系
下面通过scipy中的stats模块,模拟二项分布和泊松分布之间的关联。
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ssp,q = 0.2, 0.8
ns = [10, 500, 25000, 1250000]fig = plt.figure()
for i,n in enumerate(ns):lam = n * prs = ss.binom(n, p).rvs(50000)rv = ss.poisson(n*p)st, ed = rv.interval(0.999)xs = np.linspace(st, ed, 100)ax = fig.add_subplot(2,2,i+1)ax.hist(rs, density=True, bins='auto', alpha=0.2)ax.plot(xs, rv.pmf(xs))plt.title(f"n={n}")plt.show()
效果如下

和正态分布的关系
泊松分布是二项分布在有限时间内的极限情况,而根据中心极限定理,随着伯努利试验次数的增加,二项分布将逼近于 σ 2 = n p q , μ = n p \sigma^2=npq, \mu=np σ2=npq,μ=np的高斯分布。
在通过二项分布推导泊松分布的过程中,比较关键的一步是 λ n \frac{\lambda}{n} nλ作为概率的一个假定,当 n → ∞ n\to\infty n→∞时,可以发现 λ n \frac{\lambda}{n} nλ将趋近于0,如果继续沿用二项分布的模型,那么 q 1 ˉ − λ n − > 0 q\=1-\frac{\lambda}{n}->0 q1ˉ−nλ−>0,从而 n p q ≈ n p npq\approx np npq≈np。
由此可以得到,当事件趋近于无穷多时,泊松分布将趋近于 μ = λ , σ 2 = λ \mu=\lambda, \sigma^2=\lambda μ=λ,σ2=λ的正态分布。
下面对这个关系进行测试
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ssp = 0.1
#lam = 100
ns = [10, 500, 25000, 1250000]fig = plt.figure()
for i,n in enumerate(ns):lam = 0.1 * nrs = ss.poisson(lam).rvs(n)rv = ss.norm(lam, np.sqrt(lam))st, ed = rv.interval(0.999)xs = np.linspace(st, ed, 100)ax = fig.add_subplot(2,2,i+1)ax.hist(rs, density=True, bins='auto', alpha=0.2)ax.plot(xs, rv.pdf(xs))plt.title(f"n={n}")plt.show()
效果如下

相关文章:

【分布族谱】泊松分布和二项分布、正态分布的关系
文章目录 泊松分布和二项分布的关系和正态分布的关系 泊松分布 如果在有限时间 ( 0 , 1 ) (0,1) (0,1)内进行 n n n次伯努利实验,那么每次伯努利实验所占用的时间为 1 n \frac{1}{n} n1,按照自然规律,一件事情肯定是时间越长越容易发生&am…...

关于QTreeWidget的setData函数
当使用 Q T r e e W i d g e t I t e m QTreeWidgetItem QTreeWidgetItem 的 s e t D a t a setData setData 方法时,需要传递三个参数,分别是列索引、角色和数据。 列索引:表示要设置数据的列的索引。 Q T r e e W i d g e t I t e m QTre…...
Microsoft Office 2003的安装
哈喽,大家好。今天一起学习的是office2003的安装,这个老版本的office可是XP操作系统的老搭档了,有兴趣的小伙伴也可以来一起试试手。 一、测试演示参数 演示操作系统:Windows XP 不建议win7及以上操作系统使用 系统类型ÿ…...

使用Spring Boot和Spring Cloud实现多租户架构:支持应用多租户部署和管理
使用Spring Boot和Spring Cloud实现多租户架构:支持应用多租户部署和管理 一、概述1 什么是多租户架构?2 多租户架构的优势3 实现多租户架构的技术选择 二、设计思路1 架构选型1.1 Spring Boot1.2 Spring Cloud 2 数据库设计3 应用多租户部署3.1 应用隔离…...

智聚北京!相约全球人力资源数智化峰会
人力资源是推动经济社会发展的第一资源。作为我国经济压舱石的中央企业在对标世界一流企业和管理提升方面的持续创新,各行业领军企业围绕组织变革、管理升级、全球化发展走深走实。人力资源管理正从传统职能管理与管控,向紧贴业务战略实现、组织边界和人…...

工业缺陷检测数据及代码(附代码)
介绍 目前,基于机器视觉的表面缺陷检测设备已广泛取代人工视觉检测,在包括3C、汽车、家电、机械制造、半导体与电子、化工、制药、航空航天、轻工等多个行业领域得到应用。传统的基于机器视觉的表面缺陷检测方法通常采用常规图像处理算法或人工设计的特征加分类器。一般而言…...
CentOS 安装MongoDB 6.0
一、安装依赖 yum install libcurl openssl xz-libs 二、下载安装包 安装包下载地址https://www.mongodb.com/try/download/community这里我选择的是 选择RedHat / CentOS 7.0平台的原因是我的操作系统使用的是CentOS 7.0的,需要下载与操作系统匹配的安装包 三、…...
美团面试,被拷打了一小时....
刚从美团走出来,被拷打了一小时…越想越觉得可惜,回想面试经过,好好总结了几个点,发现面试没过的主要原因是在几个关键的问题没有给到面试官想要的答案。从而失去了这次宝贵的机会。 根据你的工作经历,说说你对质量保证…...

017+C语言中函数栈帧的创建与销毁(VS2022环境)
0.前言 您好,这里是limou3434的一篇个人博文,感兴趣的话您也可以看看我的其他文章。本次我将和您一起学习在C语言中函数栈帧的概念。 1.学习函数栈帧的意义 局部变量是怎么穿创建的?为什么局部变量的值是随机的函数是怎么传参的࿱…...

马斯克们叫停 GPT-5,更像是场行为艺术
目录 01 联名信说了什么? 02 发起方是谁? 03 谁签署了联名信? 04 联名信有哪些问题?三巨头的另外两位 Sam Altman 的表态 其他值得关注的署名者 比如马斯克。 另一个位于前列的署名者是 Stability AI 的创始人 Emad Most…...

事务基础知识
第13章 事务基础知识 1. 数据库事务概述 1.1 基本概念 **事务:**一组逻辑操作单元,使数据从一种状态变换到另一种状态。 **事务处理的原则:**保证所有事务都作为一个工作单元来执行,即使出现了故障,都不能改变这种…...

国产高性能DSP音频处理芯片的工作原理以及应用领域
DSP芯片是数字信号处理器的简称,它是一种专门用于数字信号处理的微处理器,它可以对数字信号进行高速运算和处理。DSP是一类嵌入式通用可编程微处理器,主要用于实现对信号的采集、识别、变换、增强、控制等算法处理,是各类嵌入式系…...

BEVDet4D 论文学习
1. 解决了什么问题? 单帧数据包含的信息很有限,制约了目前基于视觉的多相机 3D 目标检测方法的性能,尤其是关于速度预测任务,要远落后于基于 LiDAR 和 radar 的方法。 2. 提出了什么方法? BEVDet4D 将 BEVDet 方法从…...
:如何设计实现一个集群环境下的分布式单例模式?)
【设计模式与范式:创建型】43 | 单例模式(下):如何设计实现一个集群环境下的分布式单例模式?
上两节课中,我们针对单例模式,讲解了单例的应用场景、几种常见的代码实现和存在的问题,并粗略给出了替换单例模式的方法,比如工厂模式、IOC 容器。今天,我们再进一步扩展延伸一下,一块讨论一下下面这几个问…...
Metal入门学习:绘制渲染三角形
一、编程指南PDF下载链接(中英文档) 1、Metal编程指南PDF链接 https://github.com/dennie-lee/ios_tech_record/raw/main/Metal学习PDF/Metal 编程指南.pdf 2、Metal着色语言(Metal Shader Language:简称MSL)编程指南PDF链接 https://github.com/dennie-lee/ios_te…...
python 中常见变量类型
数值 a 10 b 123 … 字符串 在python中 用单引号’‘和双引号""括起来的都是字符串,不使用引号括起来的不是字符串,字符串是使用最多的数据类型,用来表示一段文本信息。 比如: a ‘123’ b “123” 字符串之间可以用加法运算…...
SVN使用教程(一)
文章目录 前言一、SVN是什么?二、SVN和Git对比,有什么优势?三、SVN主要应用四、SVN仓库五、安装SVN客户端 前言 提示:这里可以添加本文要记录的大概内容: 在制作系统或者写文档,都需要用于管理和跟踪开发…...

【5.19】四、性能测试—指标、种类
目录 4.1 性能测试概述 4.2 性能测试的指标 4.3 性能测试的种类 为了追求高质量、高效率的生活与工作,人们对软件产品的性能要求越来越高,例如软件产品要足够稳定、响应速度足够快,在用户量、工作量较大时也不会出现崩溃或卡顿等现象。人们…...
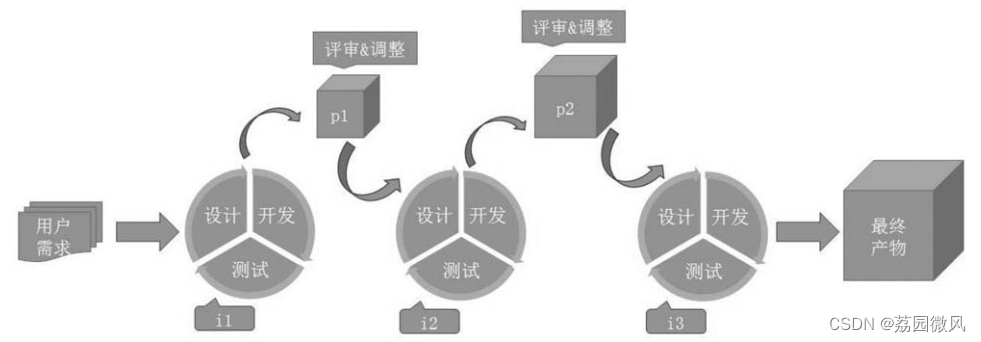
Windows平台上的5种敏捷软件开发(过程)模型
我是荔园微风,作为一名在IT界整整25年的老兵,今天总结一下Windows平台上的5种敏捷软件开发(过程)模型。 说到这个问题,你必须先知道除了敏捷模型还有没有其他什么模型?同时要比较模型的区别,首先还要看看什么叫软件开…...

一文实现部署AutoGPT
一文实现部署AutoGPT 简介AutoGPT的概述AutoGPT的用途和优势 预备知识Python基础机器学习基础自然语言处理基础 环境设置Python环境安装和配置需要的库和框架的安装,例如PyTorch, Transformers等 AutoGPT模型加载如何下载和加载预训练的AutoGPT模型模型参数和配置 使…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
