安全多方计算系列笔记1——前世今生
这一系列笔记参考了绿盟科技研究通讯的安全多方计算文章,及其他。
首先看定义:在不泄露参与方原始输入数据的前提下,允许分布式参与方合作计算任意函数,输出准确的计算结果。
起源
安全多方计算问题及解首先由姚期智(1982)提出。
问题可以解释为:两个争强好胜的富翁Alice和Bob,各自有x和y百万(单位:刀)的财富,其中1<=x,y<10。如何在不露富的前提下比较谁更是富哥?

通俗的解
假定x=4,y=6。于是Alice有4M,Bob有6M。可以用如下的步骤进行财富的比较:
- Alice准备9个箱子,分别给表面贴上1-9。
[1] [2] [3] [4] [5] [6] [7] [8] [9] - Alice在箱子里放入苹果(P)和香蕉(X)。规则是:如果箱子序号小于x,放苹果,否则放入香蕉。
[1P] [2P] [3P] [4X] [5X] [6X] [7X] [8X] [9X] - 把箱子封装后按照顺序交给Bob。此时Bob知道箱子序号(贴在外边),但是不知道里面放了什么果子。
- Bob挑选序号数字和y相等的箱子[6X],把序号撕掉[X]。
- 在Alice和Bob的共同见证下,他们打开了箱子。看看里面放的究竟是个什么玩意。
正经的解
其实知道了这个大概流程,怎么用数学来描述解、用什么样的密码学工具(模、一次性密码本、不对称密钥etc)来实现就有很多方法了。
仍然假设x=4,y=6。Alice(a)和Bob(b)都有自己的公§、私(s)钥对(分别记为pa,pb,sa,sbpa, pb, sa, sbpa,pb,sa,sb),加密和解密的操作记为:Ek(⋅)E_k(·)Ek(⋅)/Dk(⋅)D_k(·)Dk(⋅),其中k∈{pa,pb,sa,sb}k \in \{pa, pb, sa, sb\}k∈{pa,pb,sa,sb}。具体步骤为:
- Bob搞一个随机数rrr(用于封装箱子),计算m=Esb(r)−ym = E_{sb}(r)-ym=Esb(r)−y,把mmm发给Alice;
- Alice拿到mmm,因为不知道rrr是多少,所以猜不出yyy(一次性密码本的性质)。但是因为1<=x,y<10,所以Alice可以枚举y,于是他得到了[m+1,...,m+9][m+1,...,m+9][m+1,...,m+9],进而得到Boxes=[Dpb(m+1),Dpb(m+2),...,Dpb(m+9)]Boxes = [ D_{pb}(m+1), D_{pb}(m+2), ..., D_{pb}(m+9) ]Boxes=[Dpb(m+1),Dpb(m+2),...,Dpb(m+9)](生成9个箱子)。
- Alice拿一个素数ppp,ppp的数量级比rrr小。对BoxesBoxesBoxes里的9个箱子(9个数)模ppp,得到Boxesp=[Dpb(m+1)modp,Dpb(m+2)modp,...,Dpb(m+9)modp]Boxes_p = [ D_{pb}(m+1) \mod p, D_{pb}(m+2) \mod p, ..., D_{pb}(m+9) \mod p ]Boxesp=[Dpb(m+1)modp,Dpb(m+2)modp,...,Dpb(m+9)modp] 保留BoxespBoxes_pBoxesp的前xxx项,对其他项+1(放入水果、撕掉标签)。得到
Boxespf=[Dpb(m+1)modp+0,Dpb(m+2)modp+0,...,Dpb(m+9)modp+1]Boxes_{pf} = [ D_{pb}(m+1) \mod p + 0, D_{pb}(m+2) \mod p+0, ..., D_{pb}(m+9) \mod p+1 ]Boxespf=[Dpb(m+1)modp+0,Dpb(m+2)modp+0,...,Dpb(m+9)modp+1] - Alice把BoxespfBoxes_{pf}Boxespf按照序号发给Bob。此时,Bob会检查第yyy个数,看它是不是等于rmodpr \mod prmodp(打开箱子看放的什么水果)。
为什么模ppp?
读者不妨手写一下整个过程中Alice和Bob掌握的信息。如果不模个ppp,直接对BoxesBoxesBoxes中的项+0/+1的话,Bob在拿到BoxesBoxesBoxes之后就可以通过加密BoxesBoxesBoxes中的项并且和m+1,...,m+9m+1,...,m+9m+1,...,m+9进行比对,得到Alice的秘密xxx。
安全多方计算的框架模型
nnn个计算参与方分别持有各自的秘密数据
x1,x2,…,xn,x_1,x_2,…,x_n,x1,x2,…,xn,
协议的目的是利用各方的秘密数据计算一个预先达成的共识函数
(y1,y2,...,yn)=f(y1,y2,…,yn),(y_1,y_2,...,y_n)=f(y_1,y_2,…,y_n),(y1,y2,...,yn)=f(y1,y2,…,yn),
此时任意一方iii可以得到对应的结果yiy_iyi,但无法获得其他任何信息,包括其他的xxx和yyy。
在传统分布式计算模型下,传统的分布式计算由中心节点协调各用户的计算进程,收集各参与方的明文输入信息,各参与方的原始数据对第三方来说毫无秘密可言,很容易造成数据泄露。
在MPC计算模式下,不需要可信第三方收集所有参与节点的原始明文数据,只需要各参与节点之间相互交换数据即可,而且交换的是处理后(如同态加密、秘密共享等处理方法)的数据,保证其他参与节点拿到数据后,也无法反推原始明文数据,确保了各参与方数据的私密性。
安全多方计算的技术体系架构

根据支持的计算任务,可以把安全多方计算分为两类:专用场景和通用场景。
-
通用型MPC:一般由混淆电路(GC)实现,具有完备性,理论上可支持任何计算任务。具体做法是将计算逻辑编译成电路,然后混淆执行,但对于复杂计算逻辑,混淆电路的效率会有不同程度的降低,与专用算法相比效率会有很大的差距。
-
专用型MPC:为解决特定问题所构造出的特殊MPC协议,由于是针对性构造并进行优化,专用算法的效率会比基于混淆电路的通用框架高很多,当前MPC专用算法包含四则运算,比较运算,矩阵运算,隐私集合求交集,隐私数据查询等。
虽然专用型MPC与通用型MPC相比效率更高,但同样存在一些缺点,如只能支持单一计算逻辑,场景无法通用;另外专用算法设计需要领域专家针对特定问题精心设计,设计成本高。
相关文章:

安全多方计算系列笔记1——前世今生
这一系列笔记参考了绿盟科技研究通讯的安全多方计算文章,及其他。 首先看定义:在不泄露参与方原始输入数据的前提下,允许分布式参与方合作计算任意函数,输出准确的计算结果。 起源 安全多方计算问题及解首先由姚期智(…...
16- 梯度提升分类树GBDT (梯度下降优化) (算法)
梯度提升算法 from sklearn.ensemble import GradientBoostingClassifier clf GradientBoostingClassifier(subsample0.8,learning_rate 0.005) clf.fit(X_train,y_train) 1、交叉熵 1.1、信息熵 构建好一颗树,数据变的有顺序了(构建前,…...
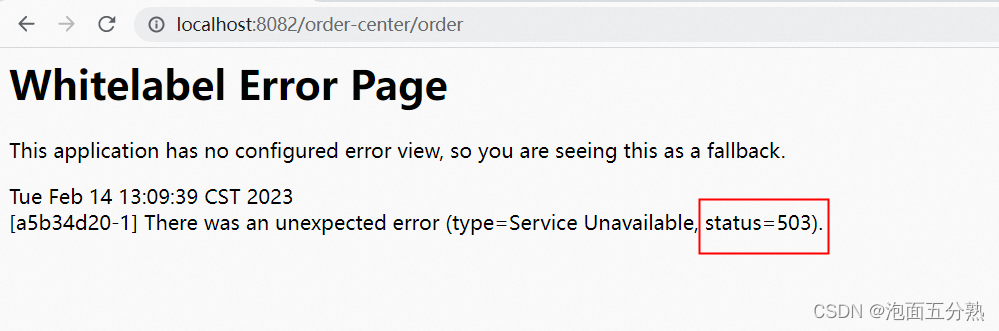
SpringCloud+Nacos+Gateway
SpringCloudNacosGatewaySpringBoot整合GatewayNacos一. 环境准备1. 版本环境2. 服务环境二. 实战1.创建用户服务2.创建订单服务3.创建网关服务4.测试三. 避坑指南问题1--503问题问题2--网关服务启动报错SpringBoot整合GatewayNacos 本篇文章只演示通过gateway网关服务访问其他…...
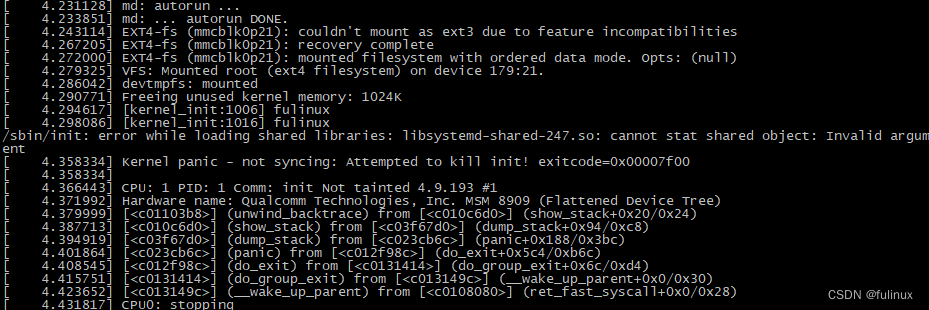
高通开发系列 - linux kernel内核升级msm-3.18升至msm-4.9(2)
By: fulinux E-mail: fulinux@sina.com Blog: https://blog.csdn.net/fulinus 喜欢的盆友欢迎点赞和订阅! 你的喜欢就是我写作的动力! 目录 返回高通开发系列 - 总目录 前面我们升级了msm-4.9内核系统正常启动了,文件系统也正常工作,但那是使用了老基线的文件系统,其yocto…...

Spring依赖注入与反转控制到底是个啥?
目录 1. 引言 2. 管中窥豹 3.1 Spring 依赖注入 3.2 Bean 的依赖注入方式有两种 4. 总结 1. 引言 此文目的是用通俗易懂的语言讲清楚什么是依赖注入与反转控制,在看了大量的博客文章后归纳总结,便于后续巩固!我相信,大多数…...

Linux Shell脚本讲解
目录 Shell脚本基础 Shell脚本组成 Shell脚本工作方式 编写简单的Shell脚本 Shell脚本参数 Shell脚本接收参数 Shell脚本判断用户参数 文件测试与逻辑测试语句 整数测试比较语句 字符串比较语句 Shell流程控制 if条件判断语句 单分支 双分支 多分支 for循环语句…...
Linux:用户空间非法指针coredump简析
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 背景 本文分析基于 ARM32 架构,Linux-4.14 内核代码。 3. 问题分析 3.1 测试范例 void main(void) {*(int *)0 8; }运行程序会 …...
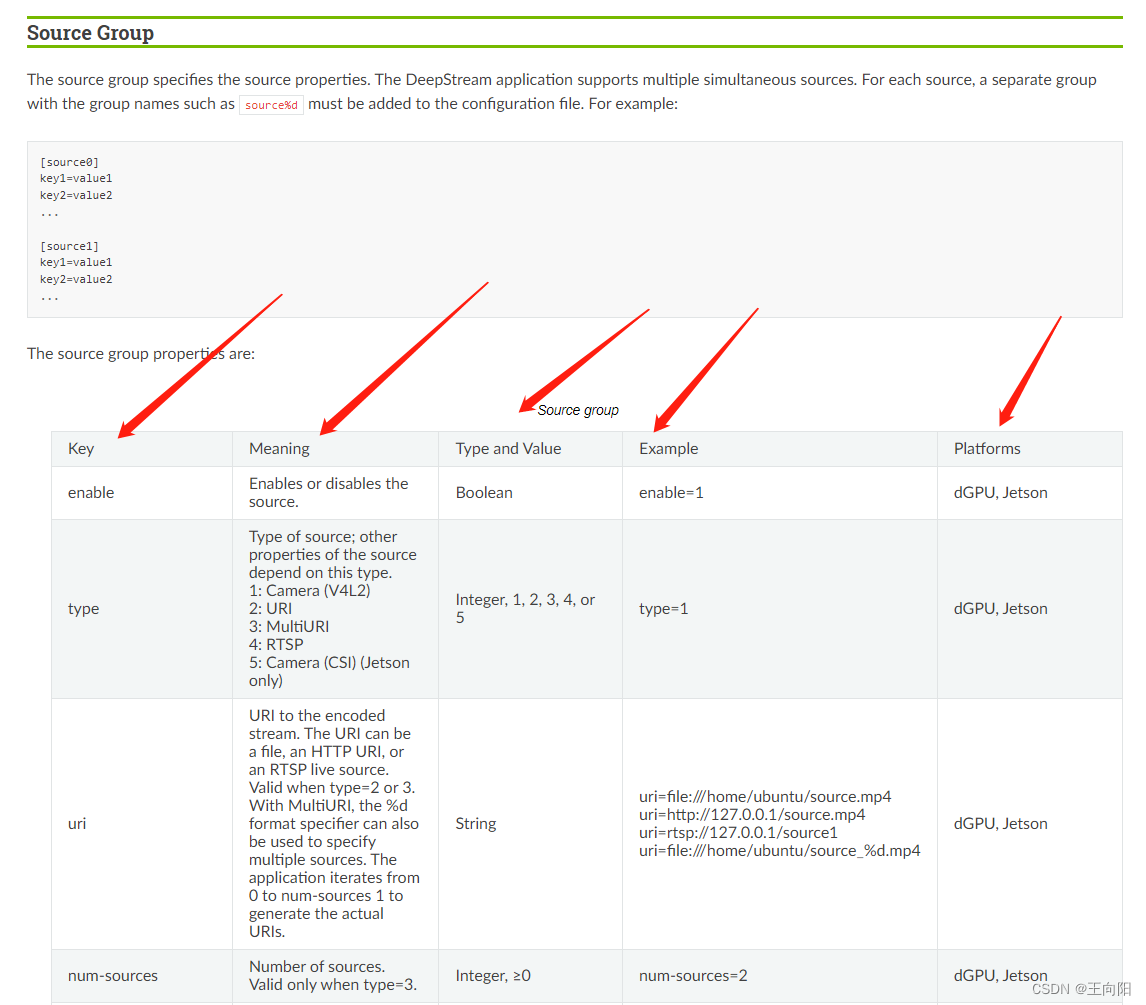
带你玩转Jetson之Deepstream简明教程(四)DeepstreamApp如何使用以及用于工程验证。
1.DeepstreamApp是什么? 如果你安装完毕deepstream整体框架,会在你的系统执行目录内有可执行文件,文件名字是deepstream-app。这是一个可执行脚本文件,通过deepstream框架中的代码在安装的时候编译后install到系统根目录内。 此脚…...
快速搭建个人在线书库,随时随地畅享阅读!
前边我们利用NAS部署了个人的导航页、小说站、云笔记,今天,我们再看看怎么部署一个个人的在线书库。 相信很多朋友都在自己的电脑中收藏了大量的PDF、MOBI等格式的电子书籍,但是一旦换了一台设备,要么是无法翻阅,要么…...

电子纸墨水屏的现实应用场景
电子纸挺好个东西,大家都把注意力集中在商超场景 其实还有更多有趣的场景方案可用,价值也不小,比如: 一、仓库场景 通过亮灯拣选,提高仓库作业效率 二、仓库循环使用标签 做NFC类发卡式应用,替代传统纸…...
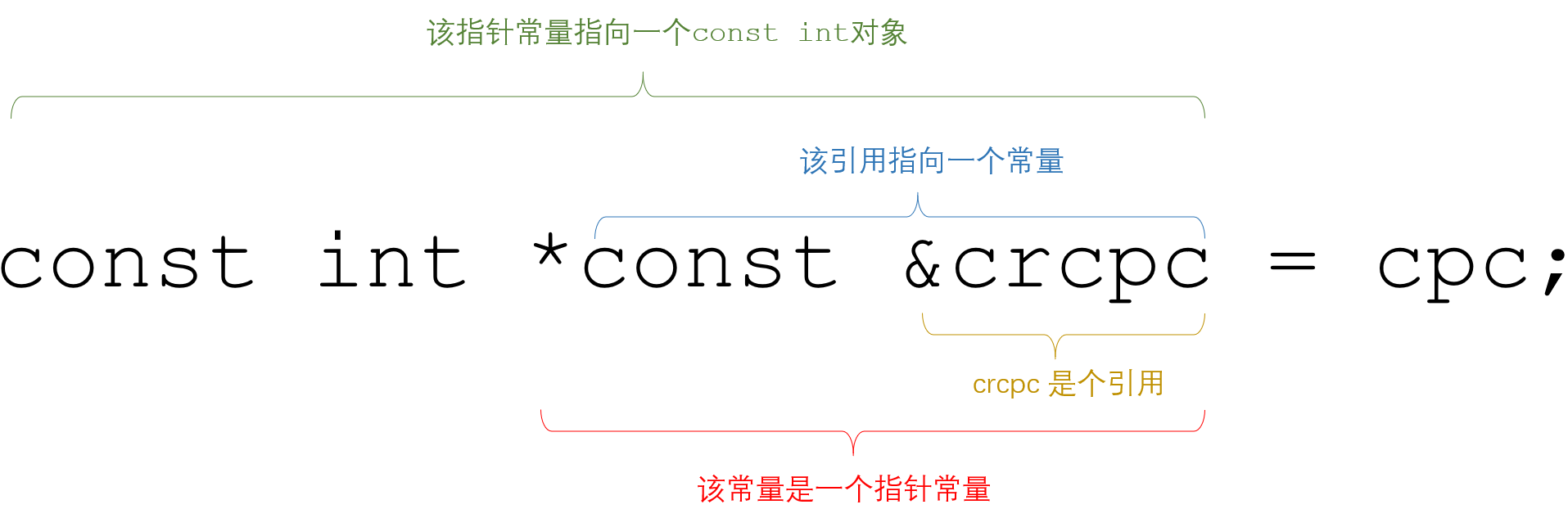
常量const、引用、指针的大杂烩
文章目录1 普通引用1.1 对普通值的普通引用1.2 对常量值的普通引用1.3 对普通指针的普通引用1.4 对常量指针的普通引用1.5 对指针常量的普通引用1.6 对指向常量的指针常量的普通引用2 常量引用2.1 对普通值的常量引用2.2 对常量值的常量引用2.3 对普通指针的常量引用2.4 对常量…...
宝塔搭建实战php开源likeadmin通用管理移动端uniapp源码(四)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享了pc端的部署方式,今天来给大家分享uniapp端在本地搭建,与打包发布到宝塔的方法。感兴趣的朋友可以自行下载学习。 技术架构 vscode node16 vue3 uniapp vite types…...

Hive的分区表与分桶表内部表外部表
文章目录1 Hive分区表1.1 Hive分区表的概念?1.1.1 分区表注意事项1.2 分区表物理存储结构1.3 分区表使用场景1.4 静态分区表是什么?1.4.1 静态分区表案例1.4.2 分区表练习一1.4.3 分区操作1.5 动态分区表是什么?1.5.1 动态态分区表案例&#…...

和数集团打造《神念无界:源起山海》,诠释链游领域创新与责任
首先,根据网上资料显示,一部《传奇》,二十年热血依旧。 《传奇》所缔造的成绩,承载的是多少人的青春回忆,《传奇》无疑已经在游戏史上写下了浓墨重彩的一笔。 相比《传奇》及背后的研发运营公司娱美德名声大噪&#x…...

小白入门模拟IC设计,如何快速学习?
众所周知,模拟电路很难学。以最普遍的晶体管来说,我们分析它的时候必须首先分析直流偏置,其次在分析交流输出电压。可以说,确定工作点就是一项相当麻烦的工作(实际中来说),晶体管的参数多、参数…...
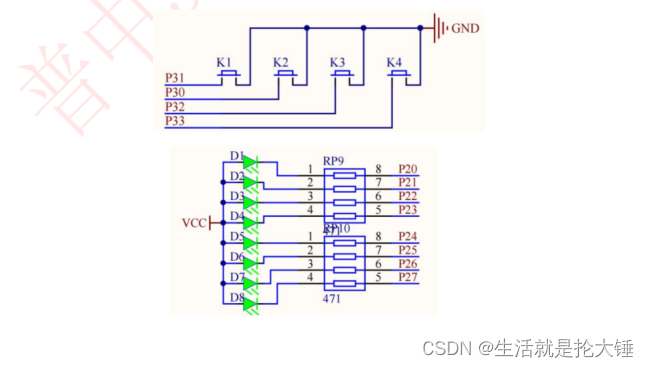
51单片机——中断系统之外部中断实验,小白讲解,相互学习
中断介绍 中断是为使单片机具有对外部或内部随机发生的事件实时处理而设置的,中断功能的存在,很大程度上提高了单片机处理外部或内部事件的能力。它也是单片机最重要的功能之一,是我们学些单片机必须要掌握的。 为了更容易的理解中断概念&…...
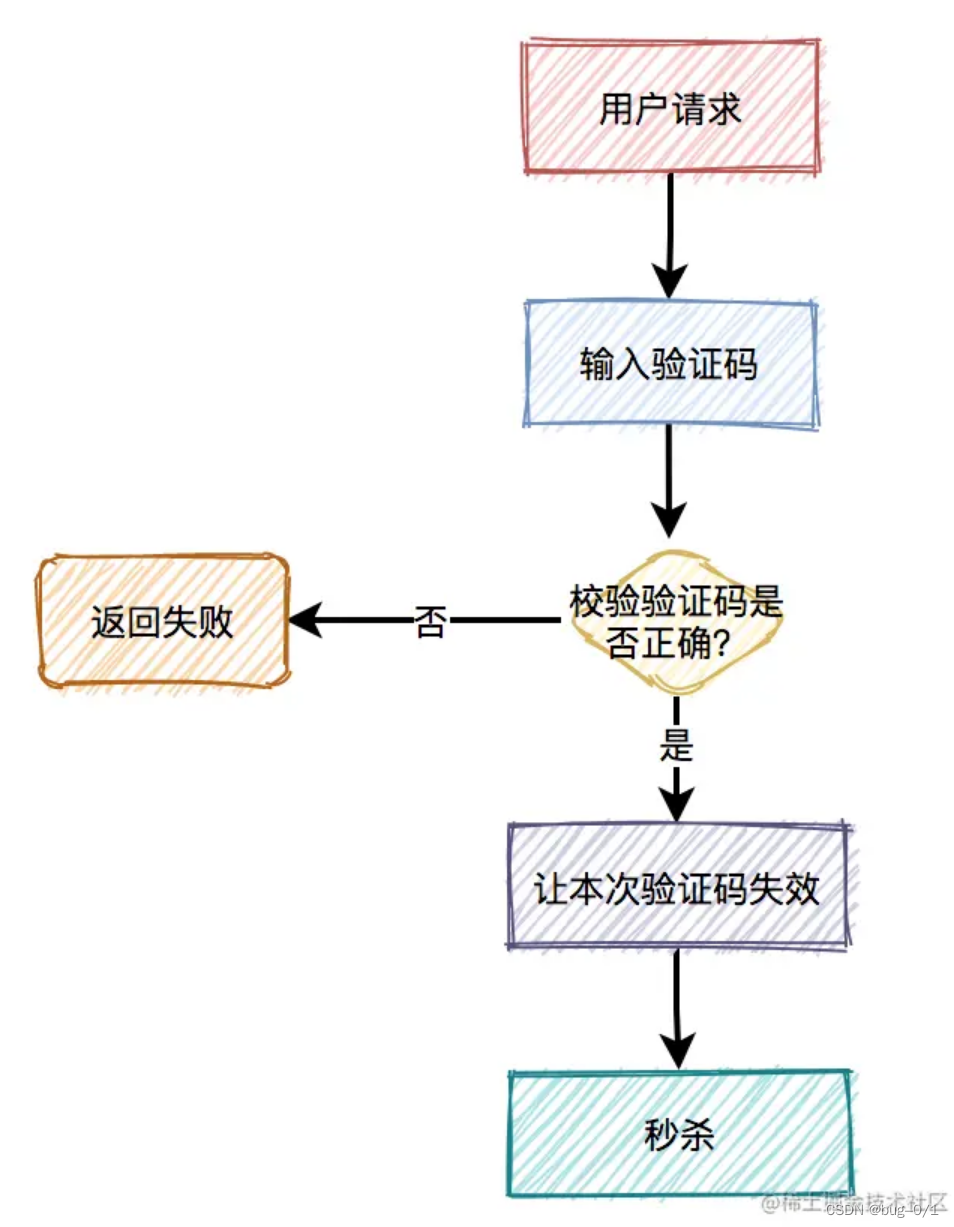
如何设计一个秒杀系统
秒杀系统要如何设计? 前言 高并发下如何设计秒杀系统?这是一个高频面试题。这个问题看似简单,但是里面的水很深,它考查的是高并发场景下,从前端到后端多方面的知识。 秒杀一般出现在商城的促销活动中,指定…...

厄瓜多尔公司注册方案
简介: 经济概况与商机 厄瓜多尔是世界上第74大国家,是南美西部国家,与哥伦比亚,秘鲁和太平洋接壤。厄瓜多尔地处世界中心,地理位置优越,地理位置优越-赤道线零纬度,使其成为通往太平洋的理想枢…...
安全渗透环境准备(工具下载)
数据来源 01 一些VM虚拟机的安装 攻击机kali: kali官网 渗透测试工具Kali Linux安装与使用 kali汉化 虚拟机网络建议设置成NAT模式,桥接有时不稳定。 靶机OWASP_Broken_Web_Apps: 迅雷下载 网盘下载 安装教程 开机之后需要登录&am…...

118.(leaflet篇)leaflet空间判断-点与geojson面图层的空间关系(turf实现)
听老人家说:多看美女会长寿 地图之家总目录(订阅之前建议先查看该博客) 文章末尾处提供保证可运行完整代码包,运行如有问题,可“私信”博主。 效果如下所示: 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYPE html> <html>...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
