由浅入深了解 深度神经网络优化算法
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理
导言
优化是从一组可用的备选方案中选择最佳方案。优化无疑是深度学习的核心。基于梯度下降的方法已经成为训练深度神经网络的既定方法。
在最简单的情况下,优化问题包括通过系统地从允许集合中选择输入值并计算函数值来最大化或最小化实函数。
在机器学习的情况下,优化是指通过系统地更新网络权重来最小化损失函数的过程。在数学上,这表示为,给定损失函数 L 和权重 w。
直观上,它可以被认为是一个高维地形的下降。如果我们可以将其投影到二维图中,则地形的高度将是损失函数的值,而水平轴将是我们的权重 w 的值。最终,我们的目标是通过反复探索我们周围的空间来到达地形的底部。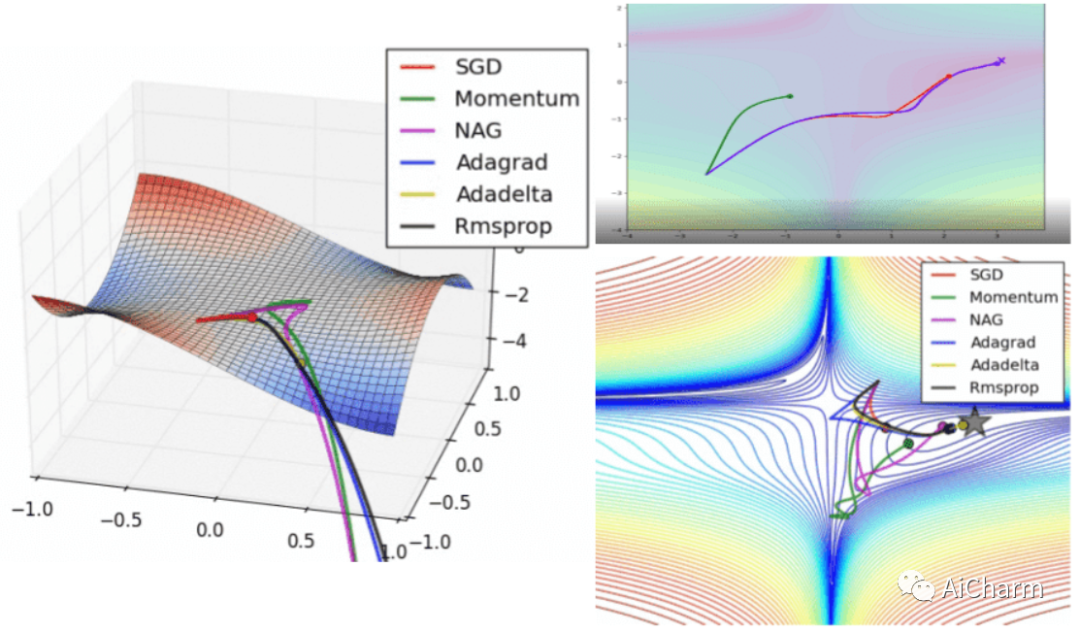
Gradient descent 梯度下降
梯度下降基于跟随地形局部坡度的基本思想。我们实质上是在混合中引入物理学和万有引力定律。微积分为我们提供了一种计算地形坡度的优雅方法,坡度是函数在该点(也称为梯度)相对于权重的导数。
_ _
learning_rate是一个常量值,称为学习率,它决定了每次迭代的步长,同时朝着损失函数的最小值移动。这可以用 Python 表示如下:
for t in range(steps): dw = gradient(loss, data, w) w = w - learning_rate *dw
在视觉上,我们可以想象下图对应一个二维空间。
实际上,在深度学习方面,梯度下降有 3 种主要的不同变体。
Batch gradient descent 批量梯度下降
上面给出的等式和代码实际上指的是批量梯度下降。在这个变体中,我们在更新权重之前计算每个训练步骤中整个数据集的梯度。
可以想象,由于我们对所有单个训练示例的损失求和,我们的计算很快就会变得非常昂贵。因此对于大型数据集来说是不切实际的。
Stochastic gradient descent 随机梯度下降
引入随机梯度下降(SGD)来解决这个确切的问题。SGD 不是计算所有训练示例的梯度并更新权重,而是更新每个训练示例的权重
_
for t in range(steps): for example in data: dw = gradient(loss, example, w) w = w - learning_rate *dw
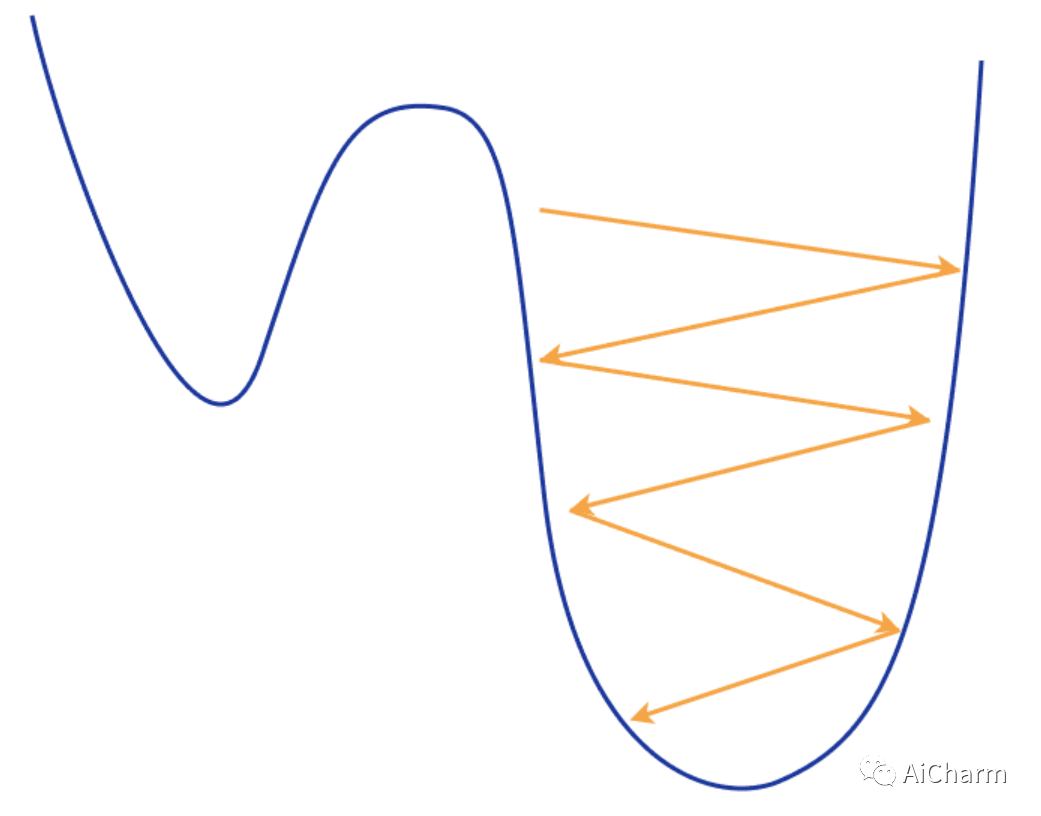
因此,SGD 速度更快,计算效率更高,但它在梯度估计中存在噪声。由于它频繁更新权重,因此会导致较大的振荡,从而使训练过程非常不稳定。
你可以想象我们不断地沿着地形走锯齿形,这导致不断超调并错过我们的最小值。尽管出于同样的原因,我们可以轻松地摆脱局部最小值并继续寻找更好的值。
Mini-batch Stochastic Gradient Descent 小批量随机梯度下降
小批量 SGD 恰好位于前两个想法的中间,结合了两个世界的优点。它从整个数据集中随机选择 n个训练样例,即所谓的小批量,并仅从中计算梯度。它本质上试图通过仅对数据的一个子集进行采样来近似批量梯度下降。数学上:
在实践中,小批量 SGD 是最常用的变体,因为它的计算成本低,收敛性更强。
for t in range(steps): for mini_batch in get_batches(data, batch_size): dw = gradient(loss, mini_batch, w) w = w - learning_rate *dw
Concerns on SGD SGD的一些担忧
然而,这个基本版本的 SGD 有一些限制和问题,可能会对训练产生负面影响。
如果损失函数在一个方向上快速变化而在另一个方向上变化缓慢,则可能导致梯度的高度振荡,从而使训练进度非常缓慢。
如果损失函数有局部最小值或鞍点,SGD 很可能会卡在那里而无法“跳出”并继续寻找更好的最小值。发生这种情况是因为梯度变为零,因此权重没有任何更新。
ps:鞍点是函数图形表面上的一个点,其中斜率(导数)都为零但不是函数的局部最大值。
梯度仍然有噪声,因为我们仅根据数据集的一小部分样本来估计它们。嘈杂的更新可能与损失函数的真实方向没有很好的关联。
选择一个好的损失函数是很困难的,需要用不同的超参数进行耗时的实验。
相同的学习率应用于我们所有的参数,这对于具有不同频率或重要性的特征可能会产生问题。
但是为了克服这些问题,多年来已经提出了许多改进。
Adding Momentum 添加动量
对 SGD 的一项基本改进来自添加动量的概念。借用物理学中的动量原理,我们强制 SGD 保持与之前时间步相同的方向移动。为此,我们引入了两个新变量:速度和摩擦力
速度 v 被计算为直到这个时间点的梯度的运行平均值,并指示梯度应该继续移动的方向,摩擦力 ρ 是一个旨在衰减的常数。
在每个时间步,我们通过将先前的速度衰减 ρ 的因子来更新我们的速度,并在当前时间添加权重的梯度。然后我们在速度向量的方向上更新我们的权重
for t in range(steps): dw = gradient(loss, w) v = rho*v +dw w = w - learning_rate *v
但是我们从动量中获得了什么?
我们现在可以避开局部最小值或鞍点,因为即使小批量的梯度可能为零,我们也会继续向下移动。
动量还可以帮助我们减少梯度的振荡,因为速度矢量可以平滑这些高度变化的地形。
最后,它减少了梯度的噪声(随机性)并沿着地形更直接地行走。
Nesterov momentum
这是动量的另一种版本,称为 Nesterov 动量,以稍微不同的方式计算更新方向。
我们不是将速度向量和梯度结合起来,而是计算速度向量会将我们带到哪里,并计算此时的梯度。换句话说,如果我们只根据我们的建立速度移动,我们会发现梯度向量会是什么,并从那里计算它。
我们可以将其可视化如下:
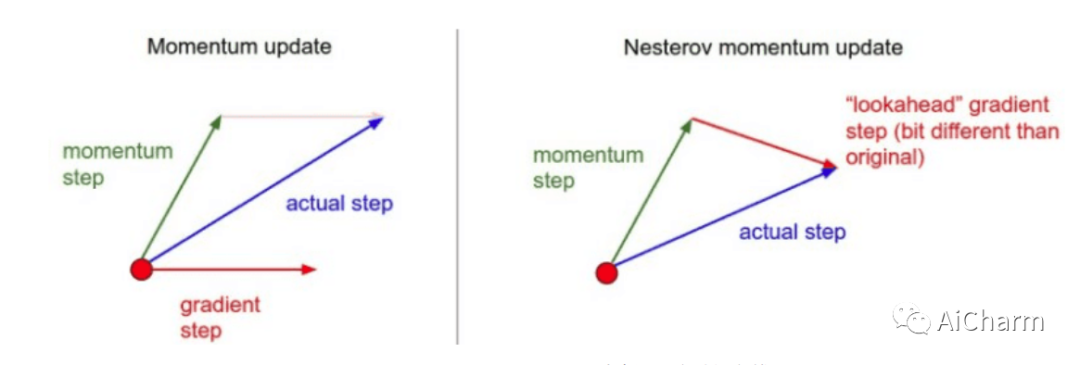
这种预期的更新可以防止我们走得太快,从而提高响应能力。最著名的利用 Nesterov 动量的算法称为 Nesterov 加速梯度 (NAG),其过程如下:
for t in range(steps): dw = gradient(loss, w) v = r*v -learning_rate*dw w = w + v
Adaptive Learning Rate 自适应学习率
优化算法的另一个重要思想是自适应学习率。直觉是我们希望对频繁的特征进行较小的更新,对不频繁的特征进行较大的更新。这将使我们能够克服之前提到的 SGD 的一些问题。
Adagrad
Adagrad 保留每个维度中梯度平方的运行总和,并且在每次更新中,我们根据总和调整学习率。这样我们就可以为每个参数实现不同的学习率(或自适应学习率)。此外,通过使用平方梯度的根,我们只考虑梯度的大小而不是符号。
⊙表示矩阵向量积
for t in range(steps): dw = gradient(loss, w) squared_gradients +=dw*dw w = w - learning_rate * dw/ (squared_gradients.sqrt() + e)
我们可以看到,当梯度变化非常快时,学习率会变小。当梯度变化缓慢时,学习率会更大。Adagrad的一大缺点是随着时间的推移,由于运行平方和的单调递增,学习率越来越小。
RMSprop
这个问题的解决方案是对上述算法进行修改,称为 RMSProp,可以将其视为“Leaky Adagrad”。本质上,我们通过衰减先前平方梯度的总和再次添加摩擦的概念。
正如我们在基于动量的方法中所做的那样,我们将项(此处为运行平方和)乘以常数值(衰减率)。这样我们希望算法不会像 Adagrad 那样在训练过程中变慢
for t in range(steps): dw = gradient(loss, w) squared_gradients = decay_rate*squared_gradients + (1- decay_rate)* dw*dw w = w - learning_rate * (dw/(squared_gradients.sqrt() + e)
可以看到分母是梯度的均方根误差 (RMS),因此是算法的名称。在大多数自适应速率算法中,添加了一个非常小的值 e 以防止分母无效。通常它等于 。
Adam
Adam(自适应矩估计)可以说是当今最流行的变体。它已广泛用于研究和商业应用。它的流行在于它结合了以前最好的两个想法。动量和自适应学习率。
我们现在跟踪两个运行变量,速度和我们在 RMSProp 上描述的平方梯度平均值。它们在原始论文中也被称为第一和第二时刻。
_δ_1 和 是每个时刻的衰减率。在 Pytorch 等框架中,您还会将它们视为 和 。
for t in range(steps): dw = gradient(loss, w) moment1= delta1 *moment1 +(1-delta1)* dw moment2 = delta2*moment2 +(1-delta2)*dw*dw w = w - learning_rate*moment1/ (moment2.sqrt()+e)
我们在这里需要提到的一件事是,对于_t_=0 ,二阶矩(速度)将非常接近于零,导致除法几乎为零分母。因此梯度变化很大。为了克服这个问题,我们还在我们的时刻添加了偏差,以迫使我们的算法在开始时采取更小的步骤。
Adam 算法转换为:
for t in range(steps): dw = gradient(loss, w) moment1= delta1 *moment1 +(1-delta1)* dw moment2 = delta2*moment2 +(1-delta2)*dw*dw moment1_unbiased = moment1 /(1-delta1**t) moment2_unbiased = moment2 /(1-delta2**t) w = w - learning_rate*moment1_unbiased/ (moment2_unbiased.sqrt()+e)
请注意,由于 Adam 算法越来越受欢迎,因此已经进行了一些进一步优化的工作。两个最有前途的变体是 AdaMax 和 Nadam,大多数深度学习框架都支持它们。
AdaMax
AdaMax 将速度 时刻计算为:
这背后的直觉?Adam 根据梯度的 L2 范数值缩放二阶矩。然而,我们可以扩展这个原则来使用无穷范数 。已经表明, 还提供稳定的行为,AdaMax 有时可以比 Adam 具有更好的性能(尤其是在具有嵌入的模型中)。
for t in range(steps): dw = gradient(loss, w) moment1= delta1 *moment1 +(1-delta1)* dw moment2 = max(delta2*moment2, abs(dw)) moment1_unbiased = moment1 /(1-delta1**t) w = w - learning_rate*moment1_unbiased/ (moment2+e)
Nadam
Nadam(Nesterov 加速自适应力矩估计)算法是对 Adam 的轻微修改,其中普通动量被 Nesterov 动量取代。
Nadam 通常在具有非常嘈杂的梯度或具有高曲率的梯度的问题上表现良好。它通常也提供更快的训练时间。
要结合 Nesterov 动量,一种方法是将梯度修改为 ,就像我们在 NAG 中所做的那样。然而,作者提出我们可以在算法的更新阶段更优雅地利用当前动量而不是旧动量 。结果,我们实现了 NAG 所基于的预期更新。
新动量(添加偏差后)的形状为:
速度矢量和更新规则保持不变。
AdaBelief
Adabelief 是 2020 年 提出的一种新的优化算法,它主要:
-
更快的训练收敛
-
更高的训练稳定性
-
更好的模型泛化
关键思想是根据当前梯度方向的“信念”改变步长。但是,这又是什么意思?在实践中,我们通过计算梯度随时间变化的方差而不是动量平方来增强 Adam。梯度的方差只不过是与预期(相信)梯度的距离。
换句话说,变成了
这就是 AdaBelief 和 Adam 之间的唯一区别!这样,优化器现在会考虑损失函数的曲率。如果观察到的梯度大大偏离bilief,我们不相信当前的观察并迈出一小步。
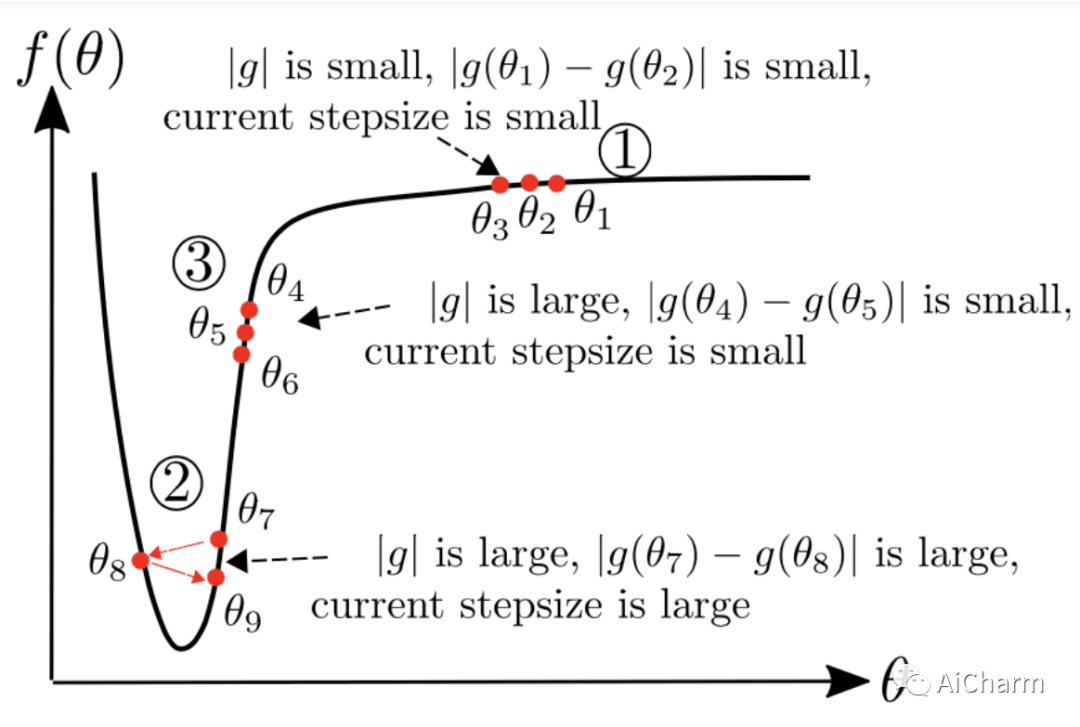
我们可以将视为对下一个梯度的预测。如果观察到的梯度接近预测,我们就相信它并迈出一大步。这在下图中变得非常清楚,其中 g 对应于
for t in range(steps): dw = gradient(loss, w) moment1= delta1 *moment1 +(1-delta1)* dw moment2 = delta2*moment2 +(1-delta2)*(dw-moment1)*(dw-moment1) moment1_unbiased = moment1 /(1-delta1**t) moment2_unbiased = moment2 /(1-delta2**t) w =w - learning_rate*moment1_unbiased/ (moment2_unbiased.sqrt()+e)
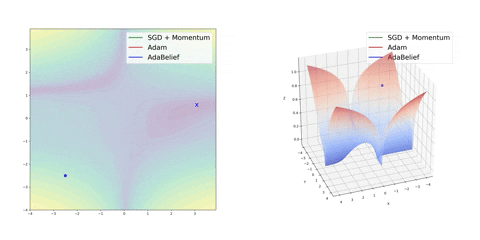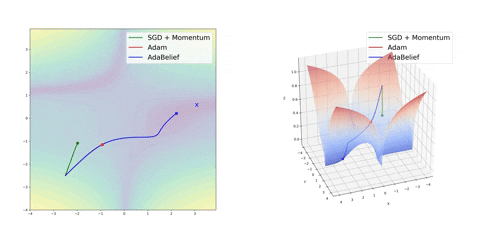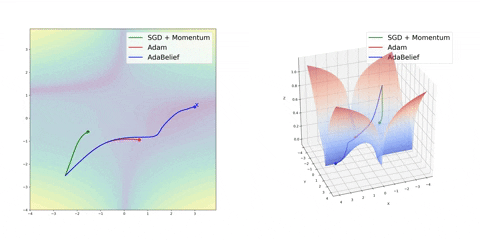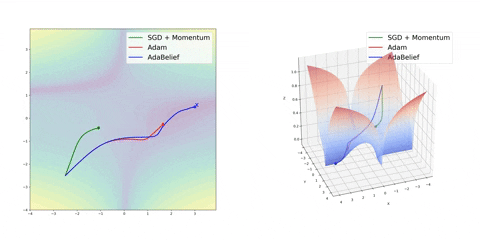
可视化优化器
如果我们查看以下可视化效果,每种算法的优缺点就会变得一目了然。
1) 具有动量的算法比基于非动量的算法具有更平滑的轨迹,但这可能会导致超调。

2)具有自适应学习率的方法具有更快的收敛速度、更好的稳定性和更少的抖动。

3)不缩放步长(自适应学习率)的算法更难逃脱局部最小值并破坏损失函数的对称性!
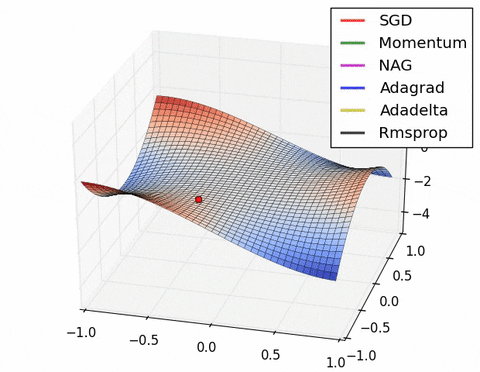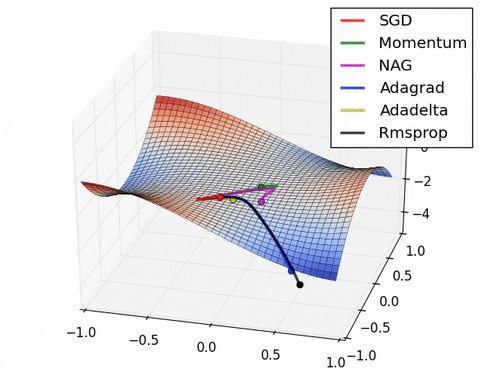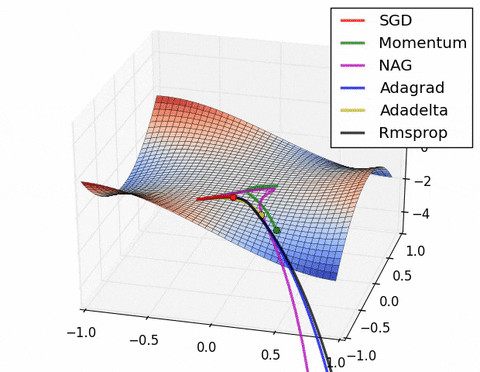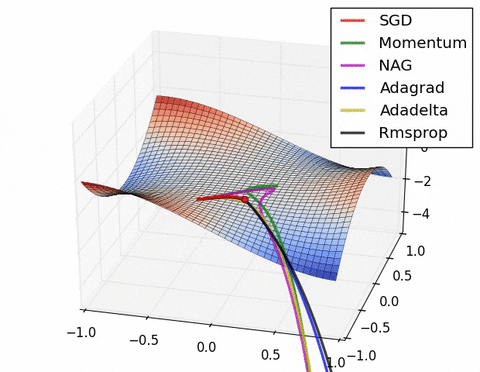
4)鞍点导致基于动量的方法在找到正确的下坡路径之前振荡
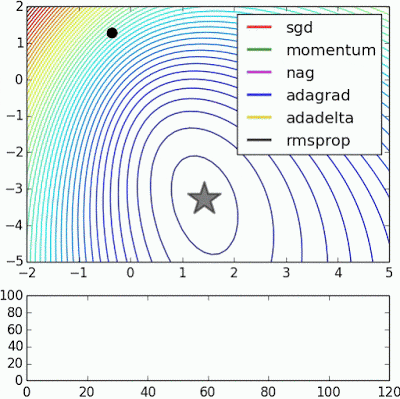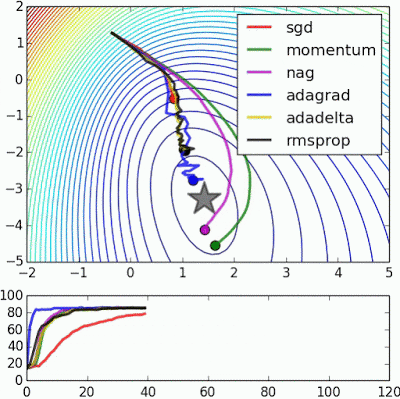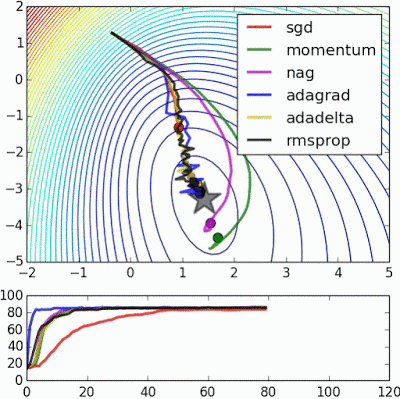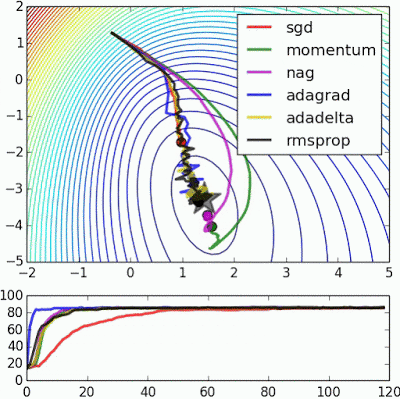
最后,AdaBelief 似乎比 Adam 更快更稳定,但现在下结论还为时过早
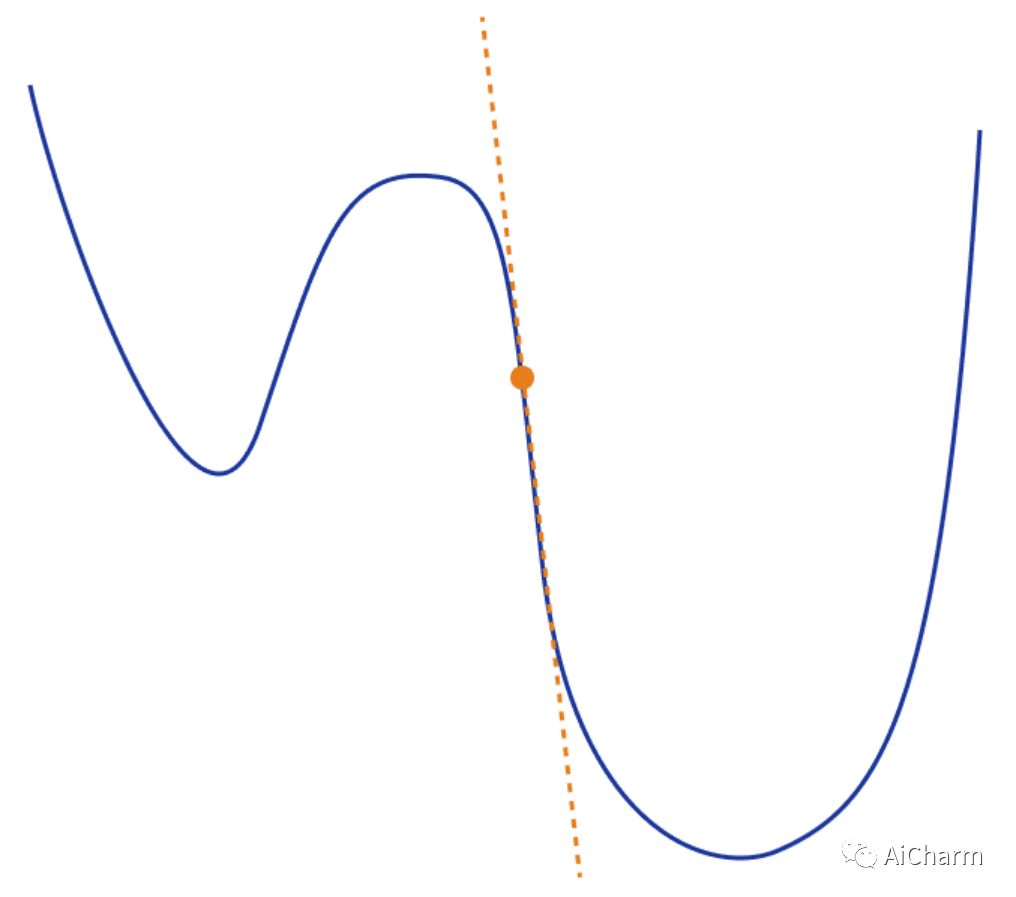
梯度下降作为损失函数的近似
考虑优化的另一种方法是近似。在任何给定点,我们都会尝试近似损失函数,以便朝正确的方向移动。梯度下降以线性形式实现了这一点。在数学上,这可以表示为点 w 周围的 L(w) 的一阶泰勒级数。
d 是我们要前进的方向。综上所述,梯度更新可以写成:
这直观地告诉我们梯度下降只是最小化局部近似.对于小的 d ,很明显近似值通常是相当合理的。随着 d变大,线性逼近将开始远离损失函数。
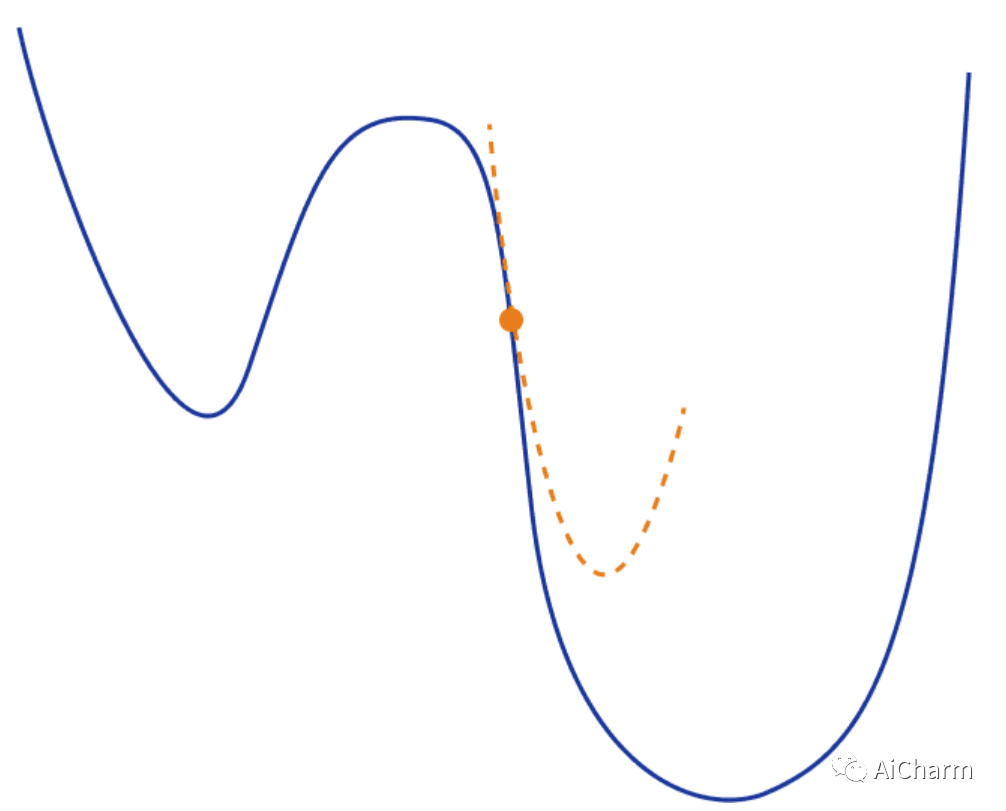
Second-order optimization 二阶优化
进过上面的学习,我们的脑海中自然而然地产生了一个疑问。我们不能使用高阶近似来获得更好的结果吗?
通过扩展上述想法,我们现在可以使用二次函数来局部逼近我们的损失函数。最常见的方法之一是再次使用泰勒级数。但是这次我们将同时保留一阶和二阶项
从视觉上看,这将如下所示:
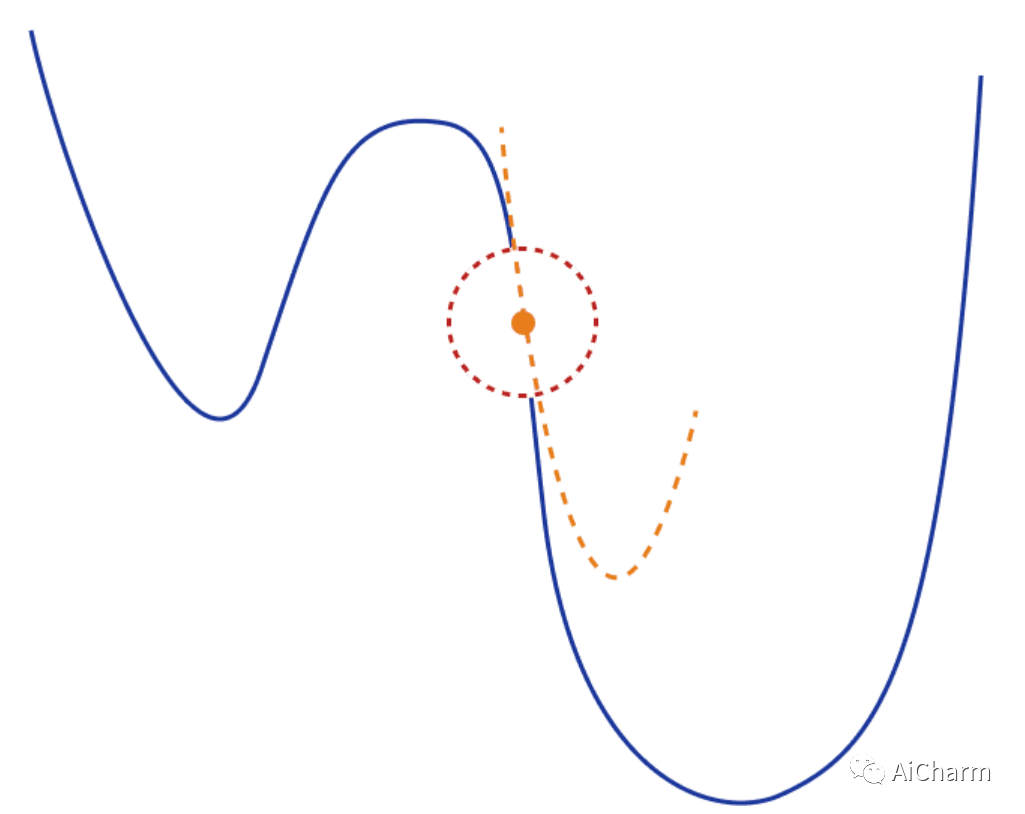
在这种情况下,梯度的更新将采用以下形式,它取决于 Hessian 矩阵 H*(w) :
有数学背景的人应该已经意识到,这无非是众所周知的牛顿法。算法的其余部分保持完全相同。另外,请注意,前面提到的许多概念(例如动量)也可以在这里应用。
二阶优化方法的缺点
二次逼近仅在小的局部区域中是可信的。当我们远离当前点(大 d )时,它可能会非常不准确。因此,我们在更新梯度时不能移动得太快。
一个常见的解决方案是将梯度更新限制在点周围的局部区域(信任区域),这样我们就可以确保近似值相当好。我们定义一个区域 r 并确保 。然后我们有:
其中取决于。
另一个常见问题是二阶泰勒级数和 Hessian 矩阵可能不是最好的二次近似。事实上,这在深度学习应用中通常是正确的。为了克服这个问题,已经提出了不同的替代矩阵:
-
Fisher information matrix Fisher 信息矩阵
-
Gradient Covariance 梯度协方差
-
Generalized Gauss-Newton 广义高斯-牛顿
最后,在这类方法中,最后也是最大的问题是计算复杂性。计算和存储 Hessian 矩阵(或任何替代矩阵)需要太多内存和资源而不实用。考虑一下,如果我们的权重矩阵具有 N 值,则 Hessian 具有 值,而逆 Hessian 具有 。这对于实际应用来说根本不可行。
总结
在这篇文章中,我们提供了深度学习中使用的不同优化算法的完整概述。我们从梯度下降的 3 种主要变体开始,继续介绍多年来提出的不同方法,最后以二阶优化结束。不过我们只是粗略地了解了每种方法的数学知识,每种方法还有更多需要学习的地方。如果你想了解更多信息,我建议您查看原始论文以获取更多详细信息。
相关文章:

由浅入深了解 深度神经网络优化算法
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 导言 优化是从一组可用的备选方案中选择最佳方案。优化无疑是深度学习的核心。基于梯度下降的方法已经成为训练深度神经网络的既定方法。 在最简单的情况下,优化问题包括通过系统地从允许集合中…...
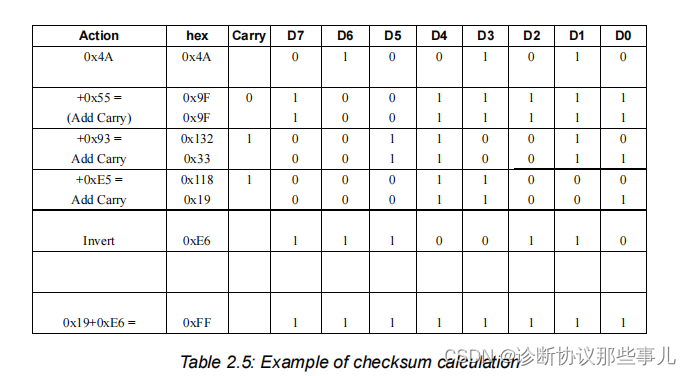
LIN-报文结构
文章目录 协议规范一、字节场二、报文头(HEADER FIELDS)同步间隔(synchronisation break)同步场(SYNCH FIELD)标识符场(IDENTIFIER FIELD) 三、数据场(DATE FIELDS)四、校…...
)
南京邮电大学通达学院2023c++实验报告(三)
题目 实验题目1 某公司财务部需要开发一个计算雇员工资的程序。该公司有3类员工,工资计算方式如下: (1)工人工资:每小时工资额(通过成员函数设定)乘以当月工作时数(通过成员函数设定),再加上工龄工资。 (2)销售员工资:每小时工资额(通过成员函数设定)乘以当月…...

ISO9000和ISO9001有哪些区别?
作为ISO标准体系的新手,ISO9000和ISO9001是第一个接触到的标准。有些人可能会含糊地表达包含关系的词语,但他们仍然无法真正理解它们。两者的关系是什么?有什么区别?事实上,两者的主要区别体现在以下三个方面: 第一&am…...

第7章异常、断言和曰志
Java和C异 在C中,throw说明符在运行时执行。Java在编译时执行。 处理错误 异常处理的任务就是将控制权从产生错误的地方转移到能够处理这种情况的错误处理器。 如果由于出现错误而使得某些操作没有完成,程序应该:返回到一种安全状态&#…...

springboot读取和写入csv文件数据
前言 csv格式的表格,和xls以及xlsx格式的表格有一些不同,不能够直接用处理xls的方式处理csv; 以下我将介绍如何读取并写入csv数据 准备工作 要处理csv格式的表格数据,我们首先需要引入pom.xml的依赖 <dependency><art…...
【产品经理】工作交接
一、前言 相信大家对这样的场景一定不陌生:有一天去找某个业务的负责人,突然被告知调岗了,或是辞职了,更坏的情况是,甚至完全找不到相关人员了,直接导致工作搁置了。这种情况,你应该多少会感到…...
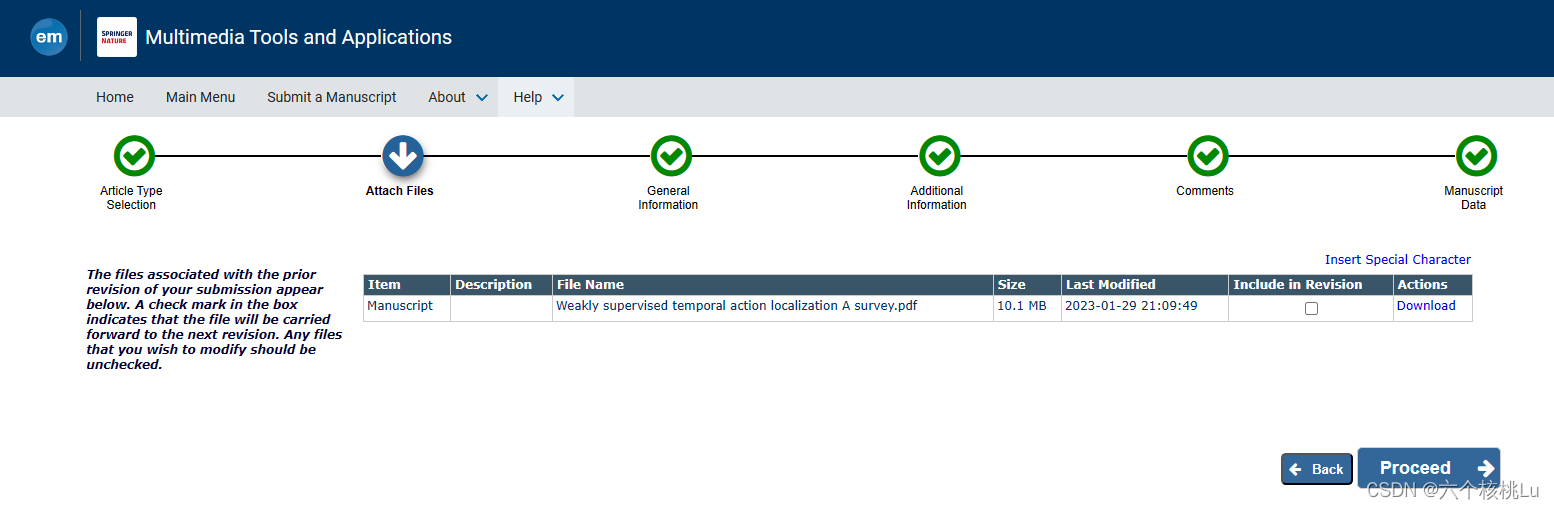
Springer期刊 latex投稿经验分享
Springer Nature期刊的latex模板下载: Download the journal article template package 以MTAP为例(修改之后对修订稿的投递过程) 第一步:将您的文章提交到适当的期刊轨道或特刊。 如有必要,从下拉菜单中更改您提交的文章类型。 然后点击Proceed 第二步: 与您提交的先前修…...

Python 文件读取的练习
读取文本文件 给定一个名为 ‘example.txt’ 的文本文件,编写一段Python代码,读取文件并打印其内容。 行数统计 给定一个名为 ‘example.txt’ 的文本文件,编写一段Python代码,计算文件中的行数。 单词统计 给定一个名为 ‘exam…...
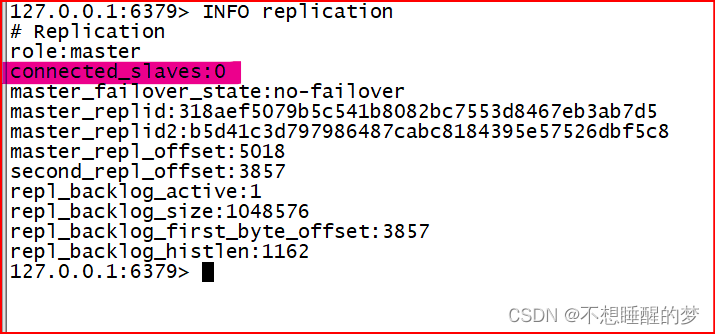
Redis:主从复制_通过此功能实现对内存上的数据更好的保护
什么是主从复制? 简单的意义上来讲就是一个主人带着几个奴隶,奴隶的全部都是主人给他的,刚开始的时候奴隶是一无所有,是主人将自己的一部分给到奴隶了。因此奴隶翻身了,变得有钱了,也就是有一定价值了&…...
LoRA:大模型的低秩自适应微调模型
对于大型模型来说,重新训练所有模型参数的全微调变得不可行。比如GPT-3 175B,模型包含175B个参数吗,无论是微调训练和模型部署,都是不可能的事。所以Microsoft 提出了低秩自适应(Low-Rank Adaptation, LoRA),它冻结了预…...
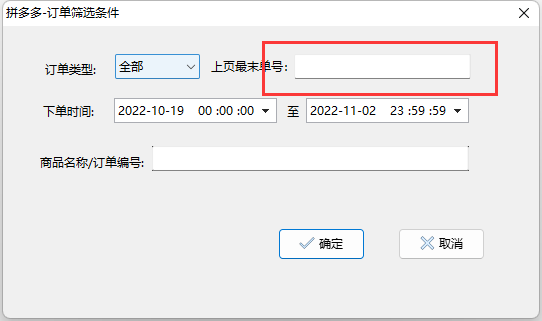
拼多多买家如何导出“个人中心”订单信息
经常在拼多多买东西,有时候需要把订单的物流信息导出来,方便记录和统计。现介绍如何使用dumuz工具来实现批量下载拼多多订单。 应用功能描述 模拟人工操作拼多多"个人中心-我的订单”订单网页,批量查询获取拼多多自己买的商品的订单数…...

11.计算机基础-计算机网络面试题—基础知识
本文目录如下: 计算机基础-计算机网络 面试题一、基础知识简述 TCP 和 UDP 的区别?http 与 https的区别?Session 和 Cookie 有什么区别?详细描述一下 HTTP 访问一个网站的过程?https 是如何实现加密的?URL是什么&…...
)
cs109-energy+哈佛大学能源探索项目 Part-1(项目背景)
1、项目概况 1.1 背景和动机 建筑能源性能的问题现在已经成为建筑业主极为关注的问题,因为这直接转化为成本。根据美国能源部的数据,建筑物消耗了美国全部能源的约40%。一些州和市政府采取了建筑节能目标,以减少城市及区域乃至全球的空气污…...

ARM Linux摄像头传感器数据处理全景视野:从板端编码视频到高级应用
ARM Linux摄像头传感器数据处理全景视野:从板端编码视频到高级应用 1. 摄像头传感器与数据采集(Camera Sensor and Data Acquisition)1.1 数字摄像头传感器基础(Basics of Digital Camera Sensors)1.1.1 传感器类型&am…...

Fixed Function Shader
Properties 属性 Shader语法不区分大小写 基础的数据类型 如何定义一个属性 属性要在"Properties{}"代码块中定义 Properties{_Color("Main Color",Color) (1,1,1,1)_Shininess("Shininess",range(0,8)) 4_MainTex("MainTex",2D…...
HTML- 标签学习之- 列表、表格
无序列表/有序列表: 标签组成( 无序ul 有序 ol ) -> li 父子级标签, ul只能包含li标签, li标签可以包含任意内容。 自定义列表 dl :自定义列表的整体,用于包裹dt/dd 标签dt:自定义列表主题dd:自定义列表的针对主题的…...

Canal搭建 idea设置及采集数据到kafka
Canal GitHub:https://github.com/alibaba/canal#readme 实时采集工具canal:利用mysql主从复制的原理,slave定期读取master的binarylog对binarylog进行解析。 canal工作原理 canal模拟MySQL slave的交互协议,伪装自己为MySQL slav…...

CentOS7搭建伪分布式Hadoop(全过程2023)
##具体操作目录## 1.配置静态ip2.关闭防火墙3.修改主机名为 *master* ,并重启虚拟机vi /etc/hostname 4.修改主机名与ip映射5.设置SSH免密登录6.安装配置java环境----------------------正式Hadoop配置1.移动安装包到合适位置2.解压安装包并重命名3.配置环境变量4.修…...
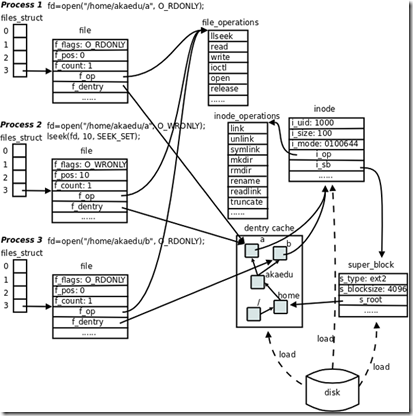
Linux中文件描述符fd和文件指针filp的理解
简单归纳:fd只是一个整数,在open时产生。起到一个索引的作用,进程通过PCB中的文件描述符表找到该fd所指向的文件指针filp。 文件描述符的操作(如: open)返回的是一个文件描述符,内核会在每个进程空间中维护一个文件描述符表, 所有打开的文件…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
