最大熵模型
最大熵模型(maximum entropy model)由最大熵原理推导实现
最大熵原理
最大熵原理是概率模型学习的一个准则。最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型时最好的模型。通常用约束条件来确定概率模型的集合,所以,最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。
假设离散随机变量 X X X的概率分布时 P ( X ) P\left(X\right) P(X),则其熵是
H ( P ) = − ∑ x P ( x ) log P ( x ) H\left(P\right) = -\sum_{x}P\left(x\right)\log P\left(x\right) H(P)=−x∑P(x)logP(x)
熵满足下列不等式:
0 ≤ H ( P ) ≤ log ∣ X ∣ 0\le H\left(P\right) \le \log \left|X\right| 0≤H(P)≤log∣X∣
其中 ∣ X ∣ \left|X\right| ∣X∣是 X X X的取值个数,当且仅当 X X X的分布是均匀分布时,右边的等号成立。
这就是说,当 X X X服从均匀分布时,熵最大
证明:
max p i − ∑ i = 1 n p i log p i s.t. ∑ i = 1 n p i = 1 \begin{aligned} &\max _{p_{i}}-\sum_{i=1}^{n} p_{i} \log p_{i} \\ &\text { s.t. } \sum_{i=1}^{n} p_{i}=1 \end{aligned} pimax−i=1∑npilogpi s.t. i=1∑npi=1
显然 − ∑ i = 1 n p i log p i ≥ 0 -\sum_{i=1}^{n} p_{i} \log p_{i} \ge 0 −∑i=1npilogpi≥0
当 p i p_i pi中其中一个为 1 1 1,其他为 0 0 0时, − ∑ i = 1 n p i log p i = 0 -\sum_{i=1}^{n} p_{i} \log p_{i} = 0 −∑i=1npilogpi=0
拉格朗日函数
L ( P , λ ) = − ∑ i = 1 n p i log p i − λ ( ∑ i = 1 n p i − 1 ) L\left(P, \lambda\right) = -\sum_{i=1}^{n} p_{i} \log p_{i} - \lambda\left(\sum_{i=1}^{n} p_{i} - 1\right) L(P,λ)=−i=1∑npilogpi−λ(i=1∑npi−1)
求导
∂ L ∂ p i = − log p i − 1 − λ = 0 \frac{\partial L}{\partial p_i} = -\log p_i - 1-\lambda =0 ∂pi∂L=−logpi−1−λ=0
于是
log p 1 = log p 2 = ⋯ = log p n = − λ − 1 \log p_1=\log p_2 = \cdots = \log p_n = -\lambda - 1 logp1=logp2=⋯=logpn=−λ−1
进而
p 1 = p 2 = ⋯ = p n p_1 = p_2=\cdots = p_n p1=p2=⋯=pn
最大熵模型的定义
最大熵原理时统计学习的一般原理,将它应用到分类得到最大熵模型
假设分类模型时一个条件概率分布 P ( Y ∣ X ) P\left(Y|X\right) P(Y∣X), X ∈ X ⊆ R n X\in\mathcal{X}\subseteq \mathbb{R}^n X∈X⊆Rn表示输入, Y ∈ Y Y\in\mathcal{Y} Y∈Y表示输出, X \mathcal{X} X和 Y \mathcal{Y} Y分别是输入和输出的集合。
这个模型表示的是对于给定的输入 X X X,以条件概率 P ( Y ∣ X ) P\left(Y|X\right) P(Y∣X)输出 Y Y Y
给定一个训练数据集
T = { ( x 1 , y 1 ) , ⋯ , ( x N , y N ) } T = \left\{\left(\mathbf{x}_1,y_1\right),\cdots,\left(\mathbf{x}_N,y_N\right)\right\} T={(x1,y1),⋯,(xN,yN)}
学习的目标是用最大熵原理选择最好的分类模型
首先考虑模型应该满足的条件。给定训练数据集,可以确定联合分布 P ( X , Y ) P\left(X,Y\right) P(X,Y)的经验分布和边缘分布 P ( X ) P\left(X\right) P(X)的经验分布,分别以 P ~ ( X , Y ) \tilde{P}\left(X,Y\right) P~(X,Y)和 P ~ ( X ) \tilde{P}\left(X\right) P~(X)表示。这里
P ~ ( X = x , Y = y ) = v ( X = x , Y = y ) N P ~ ( X = x ) = v ( X = x ) N \tilde{P}\left(X=\mathbf{x},Y=y\right)=\frac{v\left(X=\mathbf{x},Y=y\right)}{N}\\ \tilde{P}\left(X=\mathbf{x}\right) = \frac{v\left(X = \mathbf{x}\right)}{N} P~(X=x,Y=y)=Nv(X=x,Y=y)P~(X=x)=Nv(X=x)
其中, v ( X = x , Y = y ) v\left(X=\mathbf{x},Y= y\right) v(X=x,Y=y)表示训练数据中样本 ( x , y ) \left(\mathbf{x},y\right) (x,y)出现的频率, v ( X = x ) v\left(X=\mathbf{x}\right) v(X=x)表示训练数据中输入 x \mathbf{x} x出现的频率, N N N表示训练样本容量
用特征函数(feature function) f ( x , y ) f\left(\mathbf{x}, y\right) f(x,y)描述输入 x \mathbf{x} x和输出 y y y之间的某一个事实,其定义是
f ( x , y ) = { 1 , x 与 y 满足某一事实 0 , 否则 f\left(\mathbf{x},y\right) = \begin{cases} 1, & \mathbf{x}与y满足某一事实\\ 0, &否则 \end{cases} f(x,y)={1,0,x与y满足某一事实否则
特征函数 f ( x , y ) f\left(x,y\right) f(x,y)关于经验分布 P ~ ( X , Y ) \tilde{P}\left(X,Y\right) P~(X,Y)的期望值,用 E P ~ ( f ) E_{\tilde{P}}\left(f\right) EP~(f)表示
E P ~ ( f ) = ∑ x , y P ~ ( x , y ) f ( x , y ) E_{\tilde{P}}\left(f\right)=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)f\left(\mathbf{x},y\right) EP~(f)=x,y∑P~(x,y)f(x,y)
特征函数 f ( x , y ) f\left(\mathbf{x},y\right) f(x,y)关于模型 P ( Y ∣ X ) P\left(Y|X\right) P(Y∣X)与经验分布 P ~ ( X ) \tilde{P}\left(X\right) P~(X)的期望值,用 E P ( f ) E_P\left(f\right) EP(f)表示
E P ( f ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) E_P\left(f\right) = \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)f\left(\mathbf{x},y\right) EP(f)=x,y∑P~(x)P(y∣x)f(x,y)
如果模型能够获取训练数据中的信息,那么就可以假设这两个期望值相等,即
E P ( f ) = E P ~ ( f ) E_P\left(f\right)=E_{\tilde{P}}\left(f\right) EP(f)=EP~(f)
或者
∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) = ∑ x , y P ~ ( x , y ) f ( x , y ) \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)f\left(\mathbf{x},y\right)=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)f\left(\mathbf{x},y\right) x,y∑P~(x)P(y∣x)f(x,y)=x,y∑P~(x,y)f(x,y)
上式作为模型学习的约束条件
假设有 n n n个特征函数 f i ( x , y ) f_i\left(\mathbf{x},y\right) fi(x,y),那么就有 n n n个约束条件
最大熵模型:假设满足所有约束条件的模型集合为
C ≡ { P ∈ P ∣ E p ( f i ) = E P ~ ( f i ) , i = 1 , 2 , ⋯ , n } \mathcal{C}\equiv\left\{P\in\mathcal{P}|E_p\left(f_i\right) = E_{\tilde{P}}\left(f_i\right),\quad i = 1,2,\cdots, n\right\} C≡{P∈P∣Ep(fi)=EP~(fi),i=1,2,⋯,n}
定义在条件概率分布 P ( Y ∣ X ) P\left(Y|X\right) P(Y∣X)上的条件熵为
H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) H\left(P\right) = -\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)\log P\left(y|\mathbf{x}\right) H(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)
则模型集合 C \mathcal{C} C中条件熵 H ( P ) H\left(P\right) H(P)最大的模型称为最大熵模型。
(其中 log = ln = log e \log = \ln = \log_e log=ln=loge)
最大熵模型的学习
最大熵模型的学习过程就是求解最大熵模型的过程。最大熵模型的学习可以形式化为约束最大化问题
对于给定的训练数据集 T = { ( x 1 , y 1 ) , ⋯ , ( x N , y N ) } T=\left\{\left(\mathbf{x}_1,y_1\right), \cdots, \left(\mathbf{x}_N, y_N\right)\right\} T={(x1,y1),⋯,(xN,yN)}以及特征函数 f i ( x , y ) f_i\left(\mathbf{x},y\right) fi(x,y),最大熵的学习等价于约束最优化问题:
max P ∈ C H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) s . t . E P ( f i ) = E P ~ ( f i ) , i = 1 , 2 , ⋯ , n ∑ y P ( y ∣ x ) = 1 \begin{aligned} \max_{P\in \mathcal{C}} & H\left(P\right) = -\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)\log P\left(y|\mathbf{x}\right)\\ s.t.& E_P\left(f_i\right) = E_{\tilde{P}}\left(f_i\right),\quad i = 1,2,\cdots, n\\ &\sum_{y}P\left(y|\mathbf{x}\right) =1 \end{aligned} P∈Cmaxs.t.H(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)EP(fi)=EP~(fi),i=1,2,⋯,ny∑P(y∣x)=1
改成最小化
min P ∈ C − H ( P ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) s . t . E P ( f i ) = E P ~ ( f i ) , i = 1 , 2 , ⋯ , n ∑ y P ( y ∣ x ) = 1 \begin{aligned} \min_{P\in \mathcal{C}} & -H\left(P\right) = \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)\log P\left(y|\mathbf{x}\right)\\ s.t.& E_P\left(f_i\right) = E_{\tilde{P}}\left(f_i\right),\quad i = 1,2,\cdots, n\\ &\sum_{y}P\left(y|\mathbf{x}\right) =1 \end{aligned} P∈Cmins.t.−H(P)=x,y∑P~(x)P(y∣x)logP(y∣x)EP(fi)=EP~(fi),i=1,2,⋯,ny∑P(y∣x)=1
拉格朗日函数
L ( P , w ) = − H ( P ) + w 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n w i ( E P ~ ( f i ) − E P ( f i ) ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) + w 0 ( 1 − ∑ y P ( y ∣ x ) ) + ∑ i = 1 n w i ( ∑ x , y P ~ ( x , y ) f ( x , y ) − ∑ x , y P ~ ( x ) P ( y ∣ x ) f ( x , y ) ) \begin{aligned} L\left(P,\mathbf{w}\right) &=-H\left(P\right) + w_0\left(1 - \sum_{y}P\left(y|\mathbf{x}\right)\right)+\sum_{i=1}^{n}w_i\left(E_{\tilde{P}}\left(f_i\right) - E_P\left(f_i\right)\right)\\ &=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)\log P\left(y|\mathbf{x}\right)+w_0\left(1 - \sum_{y}P\left(y|\mathbf{x}\right)\right)\\ &\quad +\sum_{i=1}^{n}w_i\left(\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)f\left(\mathbf{x},y\right) - \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P\left(y|\mathbf{x}\right)f\left(\mathbf{x},y\right)\right) \end{aligned} L(P,w)=−H(P)+w0(1−y∑P(y∣x))+i=1∑nwi(EP~(fi)−EP(fi))=x,y∑P~(x)P(y∣x)logP(y∣x)+w0(1−y∑P(y∣x))+i=1∑nwi(x,y∑P~(x,y)f(x,y)−x,y∑P~(x)P(y∣x)f(x,y))
原始问题
min P ∈ C max w L ( P , w ) \min_{P\in \mathcal{C}}\max_{\mathbf{w}} L\left(P,\mathbf{w}\right) P∈CminwmaxL(P,w)
对偶问题
max w min P ∈ C L ( P , w ) \max_{\mathbf{w}}\min_{P\in \mathcal{C}} L\left(P,\mathbf{w}\right) wmaxP∈CminL(P,w)
目标函数是凸的,约束条件是等式约束,于是满足广义Slater条件, 所以原始问题与对偶问题等价
设
ψ ( w ) = min P ∈ C L ( P , w ) = L ( P w , w ) \psi\left(\mathbf{w}\right) = \min_{P\in \mathcal{C}} L\left(P,\mathbf{w}\right)=L\left(P_\mathbf{w},\mathbf{w}\right) ψ(w)=P∈CminL(P,w)=L(Pw,w)
其中
P w = arg min P ∈ C L ( P , w ) = P w ( y ∣ x ) P_{\mathbf{w}}=\arg\min_{P\in\mathcal{C}} L\left(P,\mathbf{w}\right) = P_{\mathbf{w}}\left(y|\mathbf{x}\right) Pw=argP∈CminL(P,w)=Pw(y∣x)
∂ L ∂ P ( y ∣ x ) = ∑ x , y P ~ ( x ) ( log P ( y ∣ x ) + 1 ) − ∑ y w 0 − ∑ x , y ( P ~ ( x ) ∑ i = 1 n w i f i ( x , y ) ) = ∑ x , y P ~ ( x ) ( log P ( y ∣ x ) + 1 − w 0 − ∑ i = 1 n w i f i ( x , y ) ) = 0 \begin{aligned} \frac{\partial L}{\partial P\left(y|\mathbf{x}\right)} &= \sum_{\mathbf{x},y} \tilde{P}\left(\mathbf{x}\right)\left(\log P\left(y|\mathbf{x}\right) + 1\right)-\sum_{y}w_0-\sum_{\mathbf{x},y}\left(\tilde{P}\left(\mathbf{x}\right)\sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right)\right)\\ &= \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)\left(\log P\left(y|\mathbf{x}\right) + 1-w_0-\sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right)\right)\\ &=0 \end{aligned} ∂P(y∣x)∂L=x,y∑P~(x)(logP(y∣x)+1)−y∑w0−x,y∑(P~(x)i=1∑nwifi(x,y))=x,y∑P~(x)(logP(y∣x)+1−w0−i=1∑nwifi(x,y))=0
在 P ~ ( x ) > 0 \tilde{P}\left(\mathbf{x}\right)>0 P~(x)>0的情况下
P ( y ∣ x ) = e x p ( ∑ i = 1 n w i f i ( x , y ) + w 0 − 1 ) = e x p ( ∑ i = 1 n w i f i ( x , y ) ) e x p ( 1 − w 0 ) P\left(y|\mathbf{x}\right) = exp\left(\sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right) + w_0 - 1\right)=\frac{exp\left(\sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right)\right)}{exp\left(1-w_0\right)} P(y∣x)=exp(i=1∑nwifi(x,y)+w0−1)=exp(1−w0)exp(∑i=1nwifi(x,y))
利用 ∑ y P ( y ∣ x ) = 1 \sum_{y} P\left(y|\mathbf{x}\right) = 1 ∑yP(y∣x)=1,得
P w ( y ∣ x ) = 1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) P_{\mathbf{w}}\left(y|\mathbf{x}\right) = \frac{1}{Z_{\mathbf{w}}\left(\mathbf{x}\right)}exp\left(\sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right)\right) Pw(y∣x)=Zw(x)1exp(i=1∑nwifi(x,y))
其中
Z w ( x ) = ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) Z_{\mathbf{w}}\left(\mathbf{x}\right) = \sum_{y}exp\left(\sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right)\right) Zw(x)=y∑exp(i=1∑nwifi(x,y))
其中 Z w ( x ) Z_{\mathbf{w}}\left(\mathbf{x}\right) Zw(x)称为规范化因子;
P w = P w ( y ∣ x ) P_{\mathbf{w}}=P_{\mathbf{w}}\left(y|\mathbf{x}\right) Pw=Pw(y∣x)就是最大熵模型。这里 w \mathbf{w} w是最大熵模型中的参数向量
之后,求解
max ψ ( w ) \max\psi\left(\mathbf{w}\right) maxψ(w)
令
w ∗ = arg max w ψ ( w ) \mathbf{w}^{*} = \arg\max_{\mathbf{w}}\psi\left(\mathbf{w}\right) w∗=argwmaxψ(w)
极大似然估计
下面证明对偶函数的极大化等价于最大熵模型的极大似然估计
训练数据的经验概率分布 P ~ ( X , Y ) \tilde{P}\left(X,Y\right) P~(X,Y),条件概率分布 P ( Y ∣ X ) P\left(Y|X\right) P(Y∣X)的对数似然函数表示为
L P ~ ( P w ) = log π x , y P ( y ∣ x ) P ~ ( x , y ) = ∑ x , y P ~ ( x , y ) log P ( y ∣ x ) L_{\tilde{P}} \left(P_{\mathbf{w}}\right) = \log \pi_{\mathbf{x},y}P\left(y|\mathbf{x}\right)^{\tilde{P}\left(\mathbf{x},y\right)} =\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right) \log P\left(y|\mathbf{x}\right) LP~(Pw)=logπx,yP(y∣x)P~(x,y)=x,y∑P~(x,y)logP(y∣x)
L P ~ ( P w ) = ∑ x , y P ~ ( x , y ) log P ( y ∣ x ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x , y P ~ ( x , y ) log Z w ( x ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x P ~ ( x ) log Z w ( x ) \begin{aligned} L_{\tilde{P}}\left(P_{\mathbf{w}}\right) &= \sum_{\mathbf{x},y} \tilde{P}\left(\mathbf{x},y\right) \log P\left(y|\mathbf{x}\right)\\ &=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right) - \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)\log Z_{\mathbf{w}}\left(\mathbf{x}\right)\\ &=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right) - \sum_{\mathbf{x}}\tilde{P}\left(\mathbf{x}\right)\log Z_{\mathbf{w}}\left(\mathbf{x}\right) \end{aligned} LP~(Pw)=x,y∑P~(x,y)logP(y∣x)=x,y∑P~(x,y)i=1∑nwifi(x,y)−x,y∑P~(x,y)logZw(x)=x,y∑P~(x,y)i=1∑nwifi(x,y)−x∑P~(x)logZw(x)
接着
ψ ( w ) = ∑ x , y P ~ ( x ) P w ( y , x ) log P w ( y ∣ x ) + ∑ i = 1 n w i ( ∑ x , y P ~ ( x , y ) f i ( x , y ) − ∑ x , y P ~ ( x ) P w ( y ∣ x ) f i ( x , y ) ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) + ∑ x , y P ~ ( x ) P w ( y ∣ x ) ( log P w ( y ∣ x ) − ∑ i = 1 n w i f i ( x , y ) ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x , y P ~ ( x ) P w ( y ∣ x ) log Z w ( x ) = ∑ x , y P ~ ( x , y ) ∑ i = 1 n w i f i ( x , y ) − ∑ x , y P ~ ( x ) log Z w ( x ) \begin{aligned} \psi\left(\mathbf{w}\right) &= \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P_{\mathbf{w}}\left(y,\mathbf{x}\right)\log P_{\mathbf{w}}\left(y|\mathbf{x}\right) \\ &\quad + \sum_{i=1}^n w_i\left(\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)f_i\left(\mathbf{x},y\right) - \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P_{\mathbf{w}}\left(y|\mathbf{x}\right)f_i\left(\mathbf{x},y\right)\right)\\ &=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right) + \sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right) P_{\mathbf{w}}\left(y|\mathbf{x}\right)\left(\log P_{\mathbf{w}}\left(y|\mathbf{x}\right) - \sum_{i=1}^{n}w_if_i\left(\mathbf{x},y\right)\right)\\ &=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right)-\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)P_{\mathbf{w}}\left(y|\mathbf{x}\right)\log Z_{\mathbf{w}}\left(\mathbf{x}\right)\\ &=\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x},y\right)\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right)-\sum_{\mathbf{x},y}\tilde{P}\left(\mathbf{x}\right)\log Z_{\mathbf{w}}\left(\mathbf{x}\right)\\ \end{aligned} ψ(w)=x,y∑P~(x)Pw(y,x)logPw(y∣x)+i=1∑nwi(x,y∑P~(x,y)fi(x,y)−x,y∑P~(x)Pw(y∣x)fi(x,y))=x,y∑P~(x,y)i=1∑nwifi(x,y)+x,y∑P~(x)Pw(y∣x)(logPw(y∣x)−i=1∑nwifi(x,y))=x,y∑P~(x,y)i=1∑nwifi(x,y)−x,y∑P~(x)Pw(y∣x)logZw(x)=x,y∑P~(x,y)i=1∑nwifi(x,y)−x,y∑P~(x)logZw(x)
这样,最大熵模型的学习问题就转化为具体求解对数似然函数极大化或对偶函数极大化的问题
可以将最大熵模型写成更一般的形式
1 Z w ( x ) e x p ( ∑ i = 1 n w i f i ( x , y ) ) \frac{1}{Z_{\mathbf{w}}\left(\mathbf{x}\right)}exp\left(\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right)\right) Zw(x)1exp(i=1∑nwifi(x,y))
其中
Z w ( x ) = ∑ y e x p ( ∑ i = 1 n w i f i ( x , y ) ) Z_{\mathbf{w}}\left(\mathbf{x}\right)=\sum_{y}exp\left(\sum_{i=1}^{n}w_i f_i\left(\mathbf{x},y\right)\right) Zw(x)=y∑exp(i=1∑nwifi(x,y))
这里 x ∈ R n \mathbf{x}\in\mathbb{R}^n x∈Rn为输入, y ∈ { 1 , 2 , ⋯ , K } y\in\left\{1,2,\cdots, K\right\} y∈{1,2,⋯,K}为输出, w ∈ R n \mathbf{w}\in\mathbb{R}^n w∈Rn为权值向量, f i ( x , y ) f_i\left(\mathbf{x},y\right) fi(x,y)为任意实值特征函数
参考:
统计学习方法(李航)
相关文章:

最大熵模型
最大熵模型(maximum entropy model)由最大熵原理推导实现 最大熵原理 最大熵原理是概率模型学习的一个准则。最大熵原理认为,学习概率模型时,在所有可能的概率模型(分布)中,熵最大的模型时最好…...

微服务中网关的配置
一、添加 Spring Cloud Gateway 依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifactId> </dependency>二、配置网关路由 在application.yaml中配置如下内容:…...
Linux基本指令实现4及热键指令详解
目录 Linux热键补充: 1.bc指令: Tab键的智能补充: ctrlc键: uname指令: lscpu指令: lsmem指令: df -h指令: 关机指令: 扩展指令: Linux热键补充&#…...
系统调用与API
系统调用介绍 什么是系统调用 为了让应用程序有能力访问系统资源,也为了让程序借助操作系统做一些由操作系统支持的行为,每个操作系统都会提供一套接口,以供应用程序使用。系统调用涵盖的功能很广,有程序运行所必需的支持…...
OpenPCDet系列 | 5.4.1 DenseHead中的AnchorGenerator锚框生成模块
文章目录 AnchorGenerator模块AnchorGenerator.generate_anchors函数 AnchorGenerator模块 首先,根据点云场景将其划分为一个个grid,这个grid size是可以通过配置文件设定的点云场景方位和voxel大小计算出来的。 POINT_CLOUD_RANGE: [0, -39.68, -3, 6…...
【开发者指南】如何在MyEclipse中使用HTML或JSP设计器?(上)
MyEclipse v2022.1.0正式版下载 一、HTML & JSP 可视化设计器 本文简要介绍了 MyEclipse HTML 和 JSP Web 设计器的概念、功能和基本操作过程。这两个设计器具有相似的功能和相同的操作模型,但本文为专门针对其类型的内容。本文档中的示例是使用 MyEclipse HT…...

Node开发Web后台服务
简介 Node.js 是一个基于Google Chrome V8 引擎的 JavaScript 运行环境。Node.js 使用了一个事件驱动、非阻塞式 I/O 的模型,使其轻量又高效。Node.js 的包管理器 npm,是全球最大的开源库生态系统。 能方便地搭建响应速度快、易于扩展的网络应用&#…...

Linux下对mmap封装使用
Linux下对mmap封装使用 1、mmap简介2、Linux下mmap使用介绍2.1、mmap函数2.2、munmap函数 3、对mmap进行封装4、对封装类MEM_MAP进行测试5、mmap原理6、源代码下载 1、mmap简介 mmap即memory map,是一种内存映射文件的技术。mmap可以将一个文件或者其它对象映射到进…...
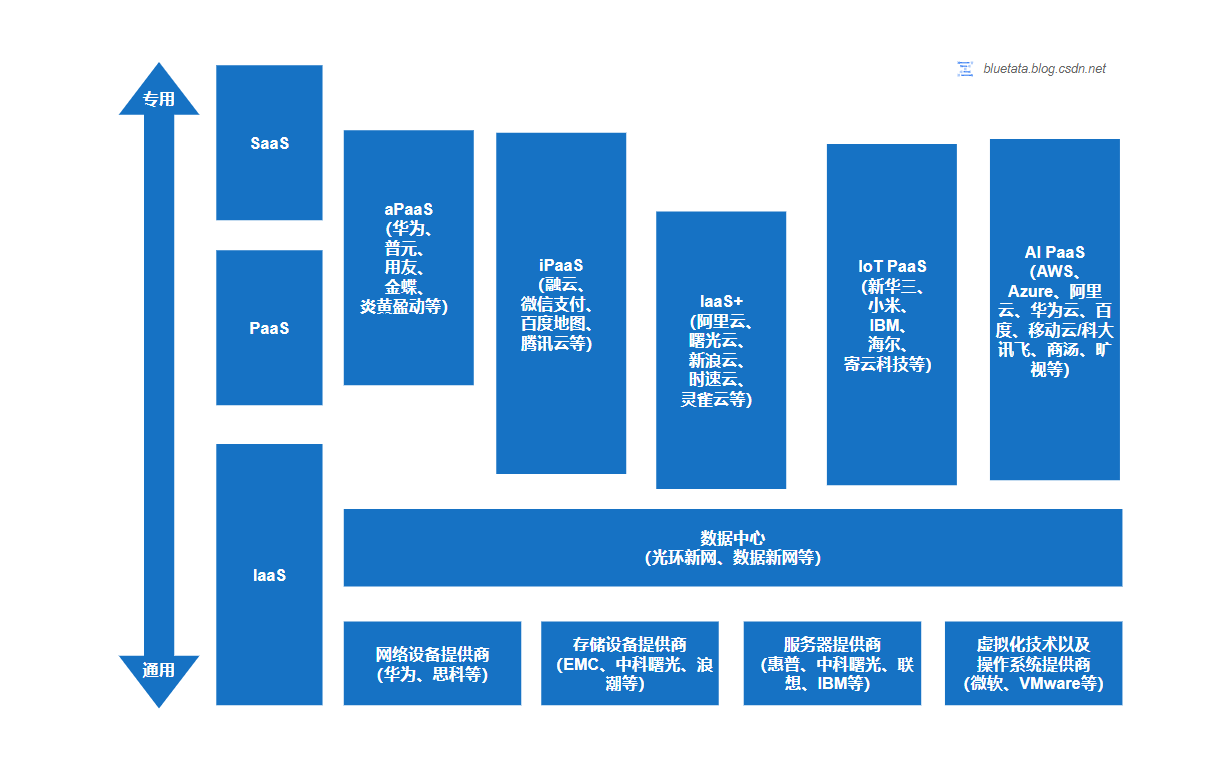
深入了解云计算:发展历程、服务与部署模型、未来趋势与挑战
开篇博主 bluetata 的观点:PaaS 服务必将是未来10年云计算权重最高的趋势(05/02/2023 15:32) 文章目录 一、前言二、认识了解云计算2.1 什么是云计算2.1.1 维基百科上的云计算定义2.1.2 NIST 标准云计算定义2.1.3 如果被面试如何解释云计算 2…...

使用乐鑫 Web IDE 助力物联网开发
乐鑫 Web IDE 是基于 Eclipse Theia 的框架,支持 ESP-IDF VS Code 插件同时具备多项辅助工具。您可以观看我们在 Espressif DevCon22 上的演示视频,了解它的实际应用。 【乐鑫开发者大会-21】搭载 ESP-IDF Visual Studio Code 插件的乐鑫 …...
---Maven的部署和发布)
Maven(5)---Maven的部署和发布
Maven的部署和发布 在前面的博客中,我们已经学习了Maven的基础知识、依赖管理、插件和生命周期,以及多模块项目管理。本篇博客将介绍Maven的部署和发布功能。 什么是部署和发布 在软件开发过程中,部署和发布是非常重要的环节。部署是指将软…...
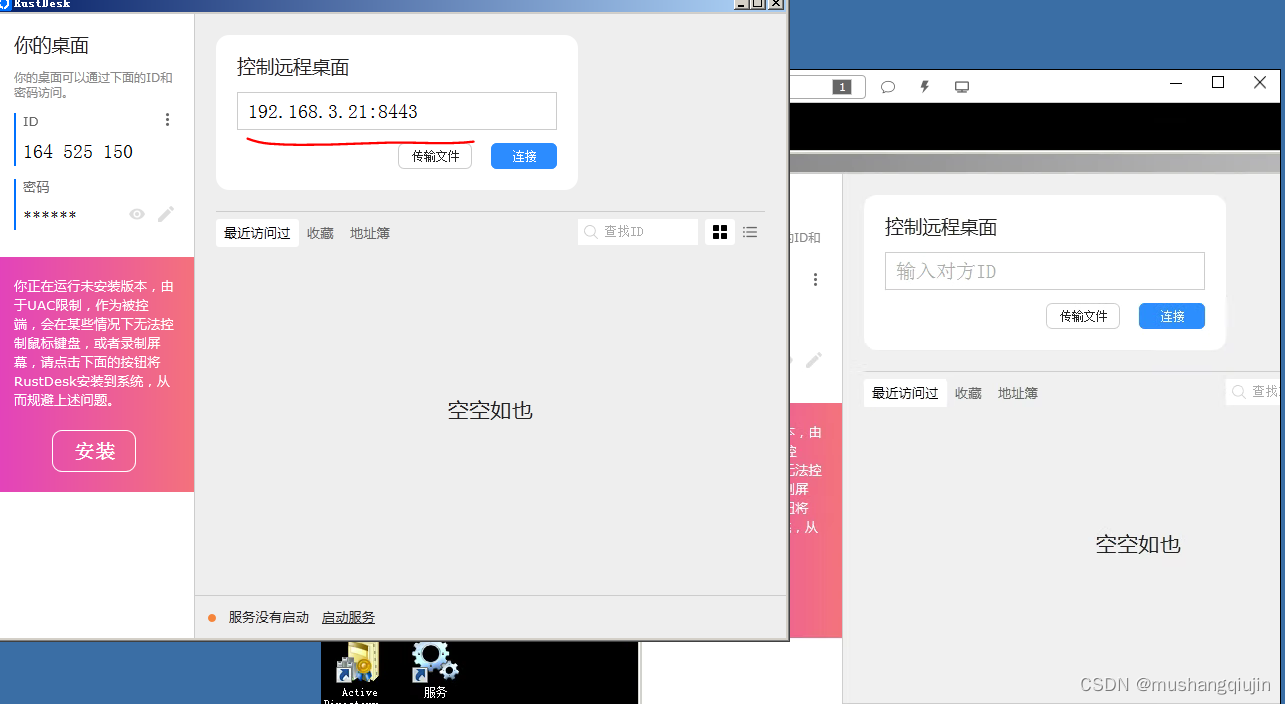
内网渗透之权限维持-黄金白银票据隐藏账户远控-RustDeskGotoHTTP
0x01权限维持-隐藏用户 CreateHiddenAccount工具 CreateHiddenAccount -u test -p Psswrd用户管理能查看到,命令查看看不到,单机版无法删除(不在任何组),域环境(在administrator组中)可以删除 0x02权限维持-黄金白银票据 ⻩⾦票据⽣成攻…...

动态规划——带权活动选择
带权活动选择Time Limit: 3000 MSMemory Limit: 1000 KB Description 给定n个活动,活动ai表示为一个三元组(si,fi,vi),其中si表示活动开始时间,fi表示活动的结束时间,vi表示活动的权重, si<fi。带权活动选择问题是选择一些活…...

软考A计划-真题-分类精讲汇总-第十八章(面向对象程序设计)
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&am…...
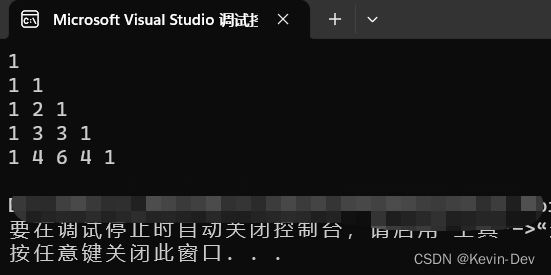
【C++ 入坑指南】(09)数组
文章目录 简介一维数组1. 定义2. 特点3. 用途4. 示例 二维数组1. 定义2. 用途3. 示例 简介 C 支持数组数据结构,它可以存储一个固定大小的相同类型元素的顺序集合。数组是用来存储一系列数据,但它往往被认为是一系列相同类型的变量。 一维数组 1. 定义…...
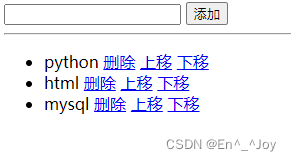
Vue.js
文章目录 Vue(前端框架)data基本语法v-bind(属性)v-if(条件)v-formethods事件v-model表单绑定todolist(添加删除展示内容,含上下移动)es6语法生命周期函数axios发送ajax请…...

博士毕业答辩流程 注意事项
前言:2023年5月17日14:00-17:00,与实验室其他同学一起旁听了本实验室的博士论文答辩。接下来,我对博士毕业答辩的大致流程进行简要介绍,并对个环节的注意事项进行总结归纳,供毕业生参考。 目录 1. 准备阶段2. 汇报期间…...

拼多多开放平台订单详情接口解析
API接口订单接口是指用于实现订单相关操作的程序接口。通过这个接口,用户可以实现创建、修改、查询和取消订单等功能。 常见的API接口订单接口包括: 创建订单接口,用于实现用户下单操作。 修改订单接口,用于修改已有订单信息。 …...
如何把ipa文件(iOS安装包)安装到iPhone手机上? 附方法汇总
苹果APP安装包ipa如何安装在手机上?很多人不知道怎么把ipa文件安装到手机上,这里就整理了苹果APP安装到iOS设备上的方式,仅供参考 苹果APP安装包ipa如何安装在手机上?使用过苹果手机的人应该深有感触,那就是苹果APP安…...
由浅入深了解 深度神经网络优化算法
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 导言 优化是从一组可用的备选方案中选择最佳方案。优化无疑是深度学习的核心。基于梯度下降的方法已经成为训练深度神经网络的既定方法。 在最简单的情况下,优化问题包括通过系统地从允许集合中…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
