加速度传感器的量程估算
下面推导过程中包含一个重要的错误:sinx/x=1没有错,但是这里的x是 t,当x = t时,位移并非sin(t),而是n*sin(t),我稍後修訂。
在测震动和噪声的场合,现有的加速度传感器,需要客户提供加速度值的大致区间。这个值该怎么计算呢?它几乎完全与被测信号的频率有关。因为所有的信号,按照频域展开的视角,都会简化为一个个正弦波。对于正弦波有这样的属性:
过零点的速度是1米/秒。因为当x->0, sinx/x = 1,在pi/2的位置,纵向位移=0,此时速度=0.
所以,宏观的加速度:
a = v(0) - v(pi/2) /timespan(pi/2)
一个周期的流逝时间是1/f, pi/2流失的时间是1/4*(1/f) = 1/(4*f)
所以,加速度:a = 1 / (1/(4*f))
a = 4*freq所以,对于工频信号50 Hz,如果这个电源震荡表现为机械震荡,那么加速度 = 4*50 = 200 m/s^2.
换算成重力加速度的G,需要除以重力加速度9.8.
大约20个G。
三相电机,一般极对数是3,机械振动的基频要除以3,所以,最终的加速度值:6.67G
震动分析时,一般可能还需要分析一些谐振,你的频谱需要扩展到高频谐波。需要扩展几倍,最终的加速度传感器的量程直接乘以多少即可。
附上几个额外的消息,大概了解一下,这种震动的测量值区间:
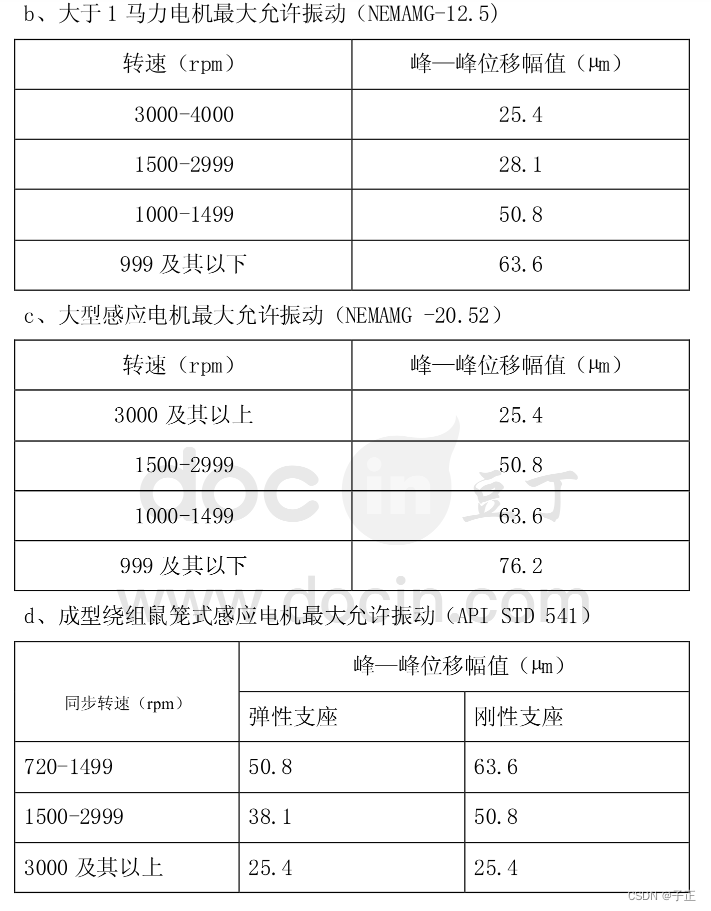
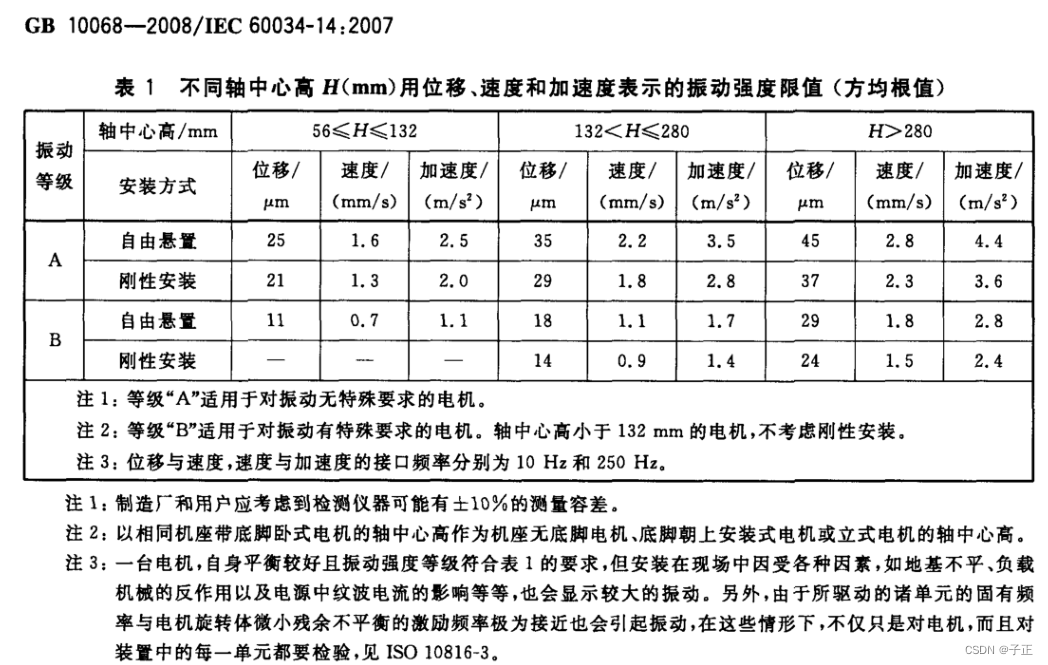
我无法解释GB10068-2008那个加速度值为什么会那么小。实际的设备在额定功率下运行,会有转差率的概念,但是此时,转速仍然与额定转速相差不会太大。如果转速体现为震动,则上述的推导过程仍然近似适用,误差不会超过5%。所以,GB10068-2008那个加速度指标到底是什么?它是设备本身的一个本征震动。并不是完全由转速得来?
大概计算一下:
如果位移是45um,这个位移可能指PkPk,
那么速度 = 45e-6/(1/50*3/2) = 1.5 mm/s 奇怪,这里与GB10068-2008差1倍。
加速度 = 1.5e-3/s(1/50*3/4) = 0.1m/S^2, 这个值与GB10068-2008差40倍。
相关文章:

加速度传感器的量程估算
下面推导过程中包含一个重要的错误:sinx/x1没有错,但是这里的x是 t,当x t时,位移并非sin(t),而是n*sin(t),我稍後修訂。 在测震动和噪声的场合,现有的加速度传感器,需要客户提供加…...
0601-指针的基础
内存 物理存储器和存储地址空间 物理存储器:实际存在的具体存储器芯片。比如:内存条、RAM芯片、ROM芯片。 存储地址空间:对存储器编码的范围。 编码:对每个物理存储单元(一个字节)分配一个号码寻址&…...

关于K8S库中高可用的锁机制详解
简介 对于无状态的组件来说,天然具备高可用特性,无非就是多开几个副本而已;而对于有状态组件来说,实现高可用则要麻烦很多,一般来说通过选主来达到同一时刻只能有一个组件在处理业务逻辑。 在Kubernetes中,…...

常用中外文献检索网站大盘点
一、常用中文文献检索权威网站: 1、知网:是全球最大的中文数据库。提供中国学术文献、外文文献、学位论文、报纸、会议、年鉴、工具书等各类资源,并提供在线阅读和下载服务。涵盖领域包括:基础科学、文史哲、工程科技、社会科学、…...

公司招了一个00后,以为是个小年轻,没想到人家是个卷王...
公司前段缺人,也面了不少测试,结果竟然没有一个合适的。一开始瞄准的就是中级的水准,也没指望来大牛,提供的薪资也不低,面试的人很多,但平均水平很让人失望。 令我印象最深的是一个00后测试员,…...

数字化转型难?怎么转?听听厂商、CIO、CEO怎么说
数字化转型已经成为当今商业领域中的热门话题。对于许多企业来说,数字化转型是一项重要而且必不可少的战略,以适应快速变化的市场环境并保持竞争力。然而,数字化转型并不是一项容易的任务,它涉及到许多方面,需要综合考虑技术、组织和文化等因素。那么,让我们来听听一些厂…...

C++面试题汇总
C面试题汇总 1. new/delete和malloc/free:2. delete和delete[]:3. 常引用:4. overload、override、overwrite的介绍5. C是不是类型安全的?6. main 函数执行以前,还会执行什么代码?7. 数组与指针的区别&…...

OpenAi编写基于Python+OpenCV的人脸识别实现带墨镜效果
要基于Python和OpenCV实现带墨镜效果的人脸识别,你可以按照以下步骤进行操作: 安装所需的库:确保你已经安装了Python和OpenCV库。你可以使用pip命令来安装OpenCV库:pip install opencv-python。 导入必要的库:在Pytho…...

安卓闲谈吹水
一、熟练掌握 Java 语言,面向对象分析设计能力,反射原理,自定义注解及泛型,多次采用设计模式重构项目 首先我们先了解什么是对象。 1.对象是由我们自己定义的类来创建出来的。 2.对象实际上就是类的具体实现。 (对象是类的一个实…...

测试类的使用
1.在pom文件中添加依赖 <dependencies> <dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>4.12</version><scope>compile</scope> </dependency> </dependencies>2.在s…...

【物联网技术对生活的影响与展望】
随着科技日新月异的发展,物联网(IoT)技术正在快速地影响着我们的生活。它是将各种设备和物品连接在一起,通过互联网使它们可以相互交流和传递数据的技术。它的应用范围广泛,可以涵盖从智能家居到工业网络的各个领域。 …...

MySQL数据库函数详解及示例
以下是一份按照常见MySQL数据库函数,并且包含函数示例: 字符串函数 字符串函数用于处理和操作文本数据。 CONCAT:将多个字符串连接为一个字符串。SUBSTRING:提取字符串的一部分。LENGTH:返回字符串的长度。REPLACE&…...
ES6对象新增了哪些扩展?
一、属性的简写 ES6中,当对象键名与对应值名相等的时候,可以进行简写 const baz {foo:foo}// 等同于 const baz {foo} 方法也能够进行简写 const o {method() {return "Hello!";} };// 等同于const o {method: function() {return &qu…...

深入理解 Linux 内核
Linux 内核系列文章 Linux 内核设计与实现 深入理解 Linux 内核 深入理解 Linux 内核(二) Linux 设备驱动程序 Linux设备驱动开发详解 文章目录 Linux 内核系列文章前言一、绪论二、内存寻址1、内存地址2、硬件中的分段(1)段选择符…...

机器人科普--evoBOT
机器人科普--evoBOT 1 介绍2 视频3 Modular prototype4 Mechanical construction5 Hardware architecture and technology6 Autonomy und navigation7 Operation of the robot8 Technical data参考 1 介绍 The evolution of autonomous mobile robotic systems 2 视频 evoBOT…...
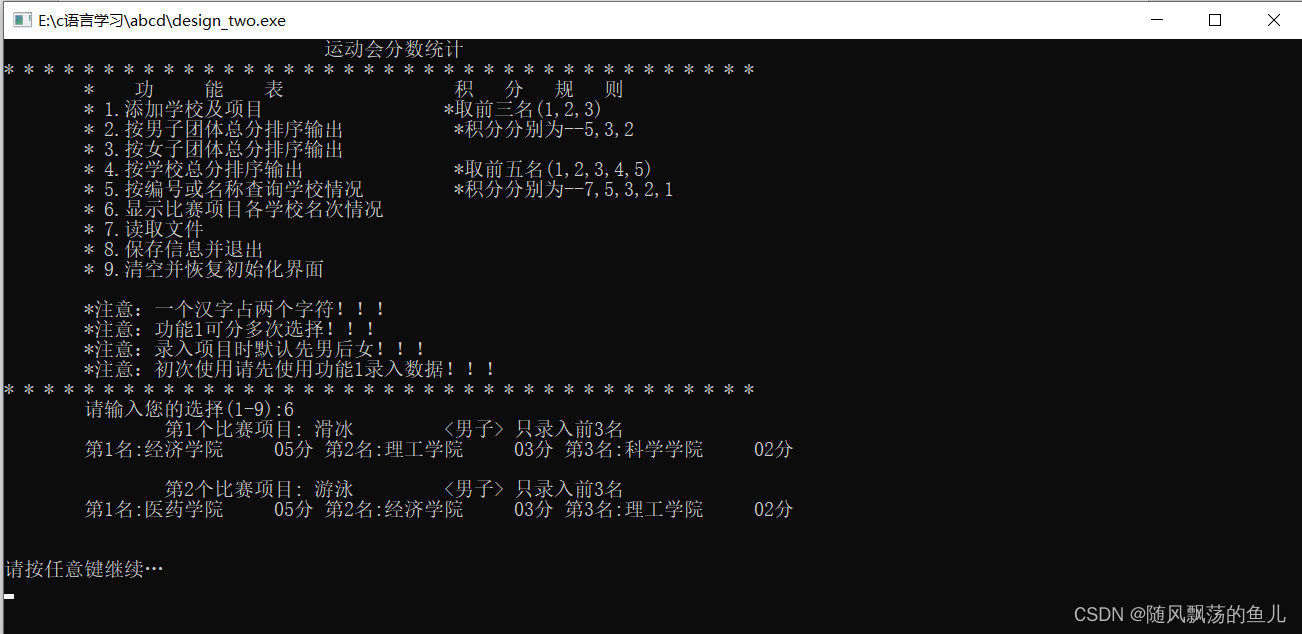
数据结构课程设计——运动会分数统计
运动会分数统计 数据结构课程设计任务书 学生姓名:xxx 专业班级:软件工程 指导教师: 工作单位: 题 目: 运动会分数统计 基础要求: 要求具有C语言的理论基础…...
C语言递归算法实现经典例题
一.递归 1.什么是递归 递归是一种编程技术,它通过在函数内部反复调用自身来解决问题。当一个程序调用自己时,这就称为递归调用。递归可以有助于简化某些算法的实现和理解。在递归过程中,每个调用都会将一些数据保存在栈上,直到递…...
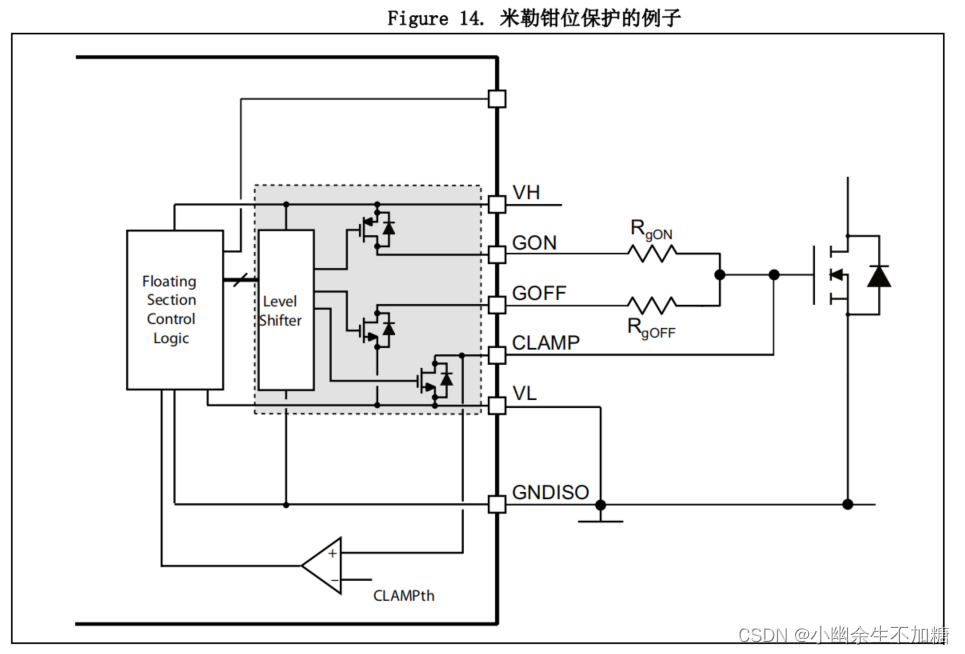
ST典型碳化硅MOSFET驱动应用方案
ST典型碳化硅MOSFET驱动应用方案 1.栅极驱动器规格和功能实现 参考资料:ST官网应用手册《AN4671》 作者:Xiou 1.栅极驱动器规格和功能实现 以下是对栅极驱动要求的简短列表: dv / dt 的瞬变抗扰度:在整个温度范围内 50 V/ns。 …...

对比AMD和英特尔显卡的区别
✨求关注~ 😀博客:www.protaos.com AMD和英特尔都是著名的半导体公司,它们都生产处理器和显卡。在显卡领域,AMD生产Radeon系列显卡,而英特尔则生产Intel HD Graphics和Intel Iris Graphics系列显卡。 使用群体对比&…...

Linux系统c语言socket实现UDP通信
UDP全称 User Datagram Protocol,即:用户数据报协议。是面向无连接的协议。通常,UDP 通信还会被冠以不可靠的头衔。这里的不可靠指的是:无法可靠地得知对方是否收到数据。 UDP有如下特征: 无连接:通信双方不需要事先连接无确认:收到数据不给对方发回执确认不保证有序、丢…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
