非线性系统的线性化与泰勒级数
线性系统与非线性系统的区别
我们在读论文的时候经常会遇到这两个系统,线性系统与非线性系统,这两者之间有什么区别呢?
线性指量与量之间按比例、成直线的关系,在空间和时间上代表规则和光滑的运动;非线性则指不按比例、不成直线的关系代表不规则的运动和突变。
在判断是否是线性系统上,主要看叠加原理(Superposition)!!!
系统的方程为 x ˙ = f ( x ) \dot x = f(x) x˙=f(x) ,如果 x 1 , x 2 x_1,x_2 x1,x2 是方程的解,有 x 3 = k 1 x 1 + k 2 x 2 ( k 1 , k 2 ∈ R ) x_3 = k_1 x_1 + k_2 x_2(k_1,k_2 \in \R) x3=k1x1+k2x2(k1,k2∈R) ,且 x 3 x_3 x3 也是方程的解,则系统符合叠加原理,为线性系统。
举个例子:
x ¨ + 2 x ˙ + 2 x = 0 ( 线性系统 ) x ¨ + 2 x ˙ + 2 x 2 = 0 ( 非线性系统 ) x ¨ + 2 s i n ( x ˙ ) + 2 x = 0 ( 非线性系统 ) \ddot x + 2 \dot x + \sqrt{2} x = 0 (线性系统) \\ \ddot x + 2 \dot x + \sqrt{2} x ^ 2 = 0 (非线性系统) \\ \ddot x + 2 sin(\dot x) + \sqrt{2} x = 0 (非线性系统) \\ x¨+2x˙+2x=0(线性系统)x¨+2x˙+2x2=0(非线性系统)x¨+2sin(x˙)+2x=0(非线性系统)
线性化方法
泰勒级数(Taylor Series)
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . + f n ( x 0 ) n ! ( x − x 0 ) n f(x) = f(x_0) + \frac{f'(x_0)}{1 !}(x-x_0) + \frac{f''(x_0)}{2 !}(x-x_0)^2 + ...+\frac{f^{n}(x_0)}{n !}(x-x_0)^n f(x)=f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!fn(x0)(x−x0)n
如果 x − x 0 → 0 x-x_0 \to 0 x−x0→0,则 ( x − x 0 ) 2 → 0 (x-x_0)^2 \to 0 (x−x0)2→0 ,则 ( x − x 0 ) n → 0 (x-x_0)^n \to 0 (x−x0)n→0 。 f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) = k 2 x + b f(x) = f(x_0) + f'(x_0)(x-x_0)=k_2x+b f(x)=f(x0)+f′(x0)(x−x0)=k2x+b,其中 k 2 = f ′ ( x 0 ) , b = f ( x 0 ) − f ′ ( x 0 ) x 0 k_2 = f'(x_0),b = f(x_0) - f'(x_0)x_0 k2=f′(x0),b=f(x0)−f′(x0)x0 。
线性化是在某一点附近的线性化,而不是全局的线性化。
一维系统,举个例子
x ¨ + x ˙ + 1 x = 1 \ddot x + \dot x + \frac{1}{x} = 1 x¨+x˙+x1=1
在平衡点(Fixed Point)附近线性化。
x ¨ = x ˙ = 0 ⇒ 1 x = 1 ⇒ x 0 = 1 \ddot x = \dot x = 0 \Rightarrow \frac{1}{x} = 1 \Rightarrow x_0 = 1 x¨=x˙=0⇒x1=1⇒x0=1
所以平衡点为 x 0 = 1 x_0 = 1 x0=1 。在 x 0 x_0 x0 附近 x δ = x 0 + x d x_{\delta} = x_0 + x_d xδ=x0+xd , 所以有
x ¨ δ + x ˙ δ + 1 x δ = 1 \ddot x_{\delta} + \dot x_{\delta} + \frac{1}{x_{\delta} } = 1 x¨δ+x˙δ+xδ1=1
运用上面的泰勒级数,先线性化 1 x δ \frac{1}{x_\delta} xδ1
f ( x δ ) = f ( x 0 ) + f ′ ( x 0 ) ( x δ − x 0 ) f(x_{\delta}) = f(x_{0}) + f'(x_0)(x_{\delta}-x_0) f(xδ)=f(x0)+f′(x0)(xδ−x0)
1 x δ = 1 x 0 + ( − 1 x 0 2 ) ( x δ − x 0 ) = 1 x 0 − x d x 0 2 = 1 − x d \frac{1}{x_\delta} = \frac{1}{x_0} + (-\frac{1}{x_0^2})(x_\delta - x_0) = \frac{1}{x_0} -\frac{x_d}{x_0^2} = 1-x_d xδ1=x01+(−x021)(xδ−x0)=x01−x02xd=1−xd
{ x ¨ δ = x ¨ 0 + x ¨ d x ˙ δ = x ˙ 0 + x ˙ d 1 x δ = 1 − x d ⇒ x ¨ 0 + x ¨ d + x ˙ 0 + x ˙ d + 1 − x d = 1 ⇒ x ¨ d + x ˙ d − x d = 0 \begin{cases} \ddot x_{\delta} = \ddot x_{0} + \ddot x_{d} \\ \dot x_{\delta} = \dot x_{0} + \dot x_{d} \\ \frac{1}{x_{\delta}} = 1 - x_d \\ \end{cases} \Rightarrow \ddot x_{0} + \ddot x_{d} + \dot x_{0} + \dot x_{d} + 1 - x_d = 1 \Rightarrow \ddot x_{d} + \dot x_{d} - x_d = 0 ⎩ ⎨ ⎧x¨δ=x¨0+x¨dx˙δ=x˙0+x˙dxδ1=1−xd⇒x¨0+x¨d+x˙0+x˙d+1−xd=1⇒x¨d+x˙d−xd=0
二维系统,举个例子
2维空间中,在平衡点附近
{ x ˙ 1 = f 1 ( x 1 , x 2 ) x ˙ 2 = f 2 ( x 1 , x 2 ) ⇒ [ x ˙ 1 d x ˙ 2 d ] = [ ∂ f 1 x 1 ∂ f 1 x 2 ∂ f 2 x 1 ∂ f 2 x 2 ] x = x 0 [ x 1 d x 2 d ] \begin{cases} \dot x_1 = f_1 (x_1,x_2) \\ \dot x_2 = f_2 (x_1,x_2) \\ \end{cases} \Rightarrow \begin{bmatrix} \dot x_{1d} \\ \dot x_{2d} \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1}{x_1} & \frac{\partial f_1}{x_2} \\ \frac{\partial f_2}{x_1} & \frac{\partial f_2}{x_2} \\ \end{bmatrix} _ {x = x_0} \begin{bmatrix} x_{1d} \\ x_{2d} \end{bmatrix} {x˙1=f1(x1,x2)x˙2=f2(x1,x2)⇒[x˙1dx˙2d]=[x1∂f1x1∂f2x2∂f1x2∂f2]x=x0[x1dx2d]
x ¨ + x ˙ + 1 x = 1 \ddot x + \dot x + \frac{1}{x} = 1 x¨+x˙+x1=1
let x 1 = x , x 2 = x ˙ x_1 = x,x_2 = \dot x x1=x,x2=x˙ ,that has
{ x ˙ 1 = x 2 x ˙ 2 = x ¨ = 1 − x ˙ − 1 x = 1 − x 2 − 1 x 1 \begin{cases} \dot x_1 = x_2 \\ \dot x_2 = \ddot x = 1- \dot x - \frac{1}{x} = 1- x_2 - \frac{1}{x_1} \end{cases} {x˙1=x2x˙2=x¨=1−x˙−x1=1−x2−x11
寻找平衡点,令 x ˙ 1 = 0 , x ˙ 2 = 0 \dot x_1 = 0,\dot x_2 = 0 x˙1=0,x˙2=0 ,则有平衡点 x 10 = 1 , x 20 = 0 x_{10} = 1,x_{20} = 0 x10=1,x20=0,
[ x ˙ 1 d x ˙ 2 d ] = [ 0 1 − ( − 1 x 1 2 ) − 1 ] x 0 [ x 1 d x 2 d ] = [ 0 1 1 − 1 ] [ x 1 d x 2 d ] \begin{bmatrix} \dot x_{1d} \\ \dot x_{2d} \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -(-\frac{1}{x_1^2}) & -1 \\ \end{bmatrix} _ {x_0} \begin{bmatrix} x_{1d} \\ x_{2d} \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} x_{1d} \\ x_{2d} \end{bmatrix} [x˙1dx˙2d]=[0−(−x121)1−1]x0[x1dx2d]=[011−1][x1dx2d]
即
{ x ˙ 1 d = x 2 d x ˙ 2 d = x 1 d − x 2 d \begin{cases} \dot x_{1d} = x_{2d} \\ \dot x_{2d} = x_{1d} - x_{2d} \end{cases} {x˙1d=x2dx˙2d=x1d−x2d
其实我们只需要下半部分
x ˙ 2 d = x 1 d − x 2 d ⇒ x ¨ d = x d − x ˙ d ⇒ x ¨ d + x ˙ d − x d = 0 \dot x_{2d} = x_{1d} - x_{2d} \Rightarrow \ddot x_d = x_d - \dot x_d \Rightarrow \ddot x_d + \dot x_d - x_d = 0 x˙2d=x1d−x2d⇒x¨d=xd−x˙d⇒x¨d+x˙d−xd=0
和上面的一维系统的等式是一样的。
总结
线性化公式, x − x 0 → 0 x-x_0 \to 0 x−x0→0
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) f(x) = f(x_0) + f'(x_0)(x-x_0) f(x)=f(x0)+f′(x0)(x−x0)
相关文章:

非线性系统的线性化与泰勒级数
线性系统与非线性系统的区别 我们在读论文的时候经常会遇到这两个系统,线性系统与非线性系统,这两者之间有什么区别呢? 线性指量与量之间按比例、成直线的关系,在空间和时间上代表规则和光滑的运动;非线性则指不按比…...
HOOPS全新文档系统上线!三维模型文件转换更便捷!
HOOPS 2023 U1版本已经正式发布,伴随新版本上线的还有全新的文档系统,新的文档系统亮点包括: 改进了样式和布局,使导航更加简单快捷;修订了导航结构,提高了产品相关信息的清晰度;SDK API参考章…...

第三篇:强化学习发展历史
你好,我是zhenguo(郭震) 这是强化学习第三篇,我们回顾一下它的发展历史:强化学习发展历史 强化学习作为一门研究领域,经历了多年的发展和演进。以下是强化学习的主要发展历史里程碑: 1950年代-1…...

如何学会战略性思维?
上帝在创造一个成功人生时加入了什么配方?一部分努力、一点天赋、必备的人脉、再加入不可或缺的good luck......这都是成功人生的重要因素。 弗雷德佩拉德认为,不管人们在商业领域选择追求什么,要想成功,还需要增加一个名为“战略…...

设备采购信息管理系统
系列文章 任务14 设备采购信息管理系统 文章目录 系列文章一、实践目的与要求1、目的2、要求 二、课题任务三、总体设计1.存储结构及数据类型定义2.程序结构3.所实现的功能函数4、程序流程图 四、小组成员及分工五、 测试界面展示添加采购信息按编号查找采购信息按设备编号查找…...
Puppeteer入门实践
环境 1、安装nodejs 官网:https://nodejs.org/zh-cn 下载安装好nodejs只后 验证:node -v 出现版本号表示安装成功,否则需要配置环境变量 2、创建node项目并初始化 随便新建一个文件夹 进入文件夹搜索cmd回车 执行npm init -y 安装依赖 …...
生成VLC 及其模块的全面帮助
使用vlc.exe -H命令生成VLC帮助文件vlc-help.txt -h, --help, --no-help 打印 VLC 帮助 (可以和 --advanced 和 --help-verbose 一起使用) (默认禁用) -H, --full-help, --no-full-help VLC 及…...

什么是客户自助服务门户及其搭建方法
随着信息技术的快速发展,越来越多的企业开始转向以客户为中心的服务模式,而客户自助服务门户(Customer Self-Service Portal)则成为了重要的服务方式。它可以让客户在不需要人工干预的情况下,自行解决问题,…...
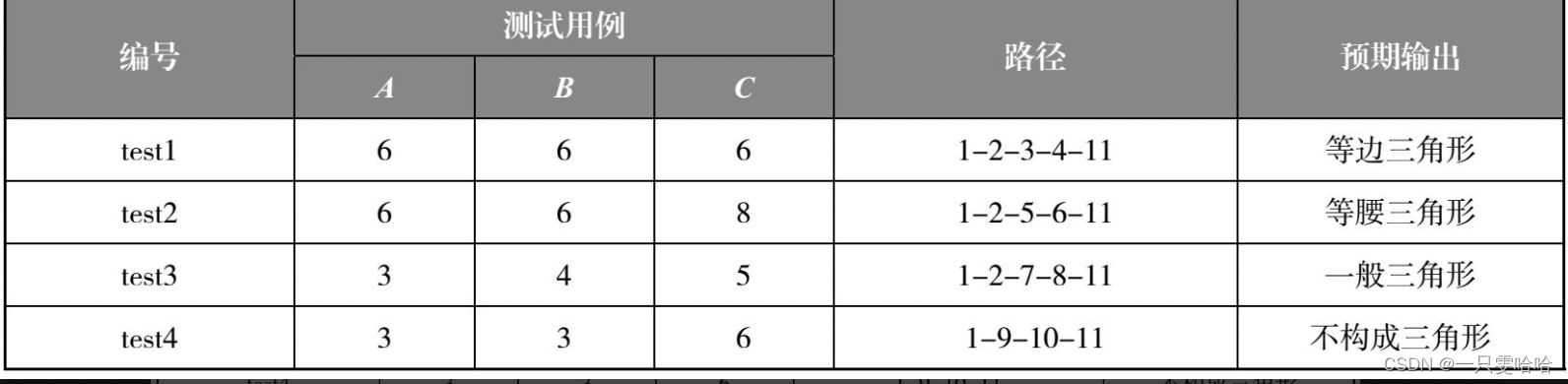
【5.19】三、白盒测试方法—逻辑覆盖法
目录 3.1 逻辑覆盖法 3.1.1 语句覆盖 3.1.2 判定覆盖 3.1.3 条件覆盖 3.1.4 判定—条件覆盖 3.1.5 条件组合覆盖 3.1.6 实例:三角形逻辑覆盖问题 白盒测试又称为透明盒测试、结构测试,它基于程序内部结构进行测试,而不是测试应用程序…...

Linux安装MySQL后无法通过IP地址访问处理方法
本文主要总结Linux安装Mysql后,其他主机访问不了MySQL数据库的原因和解决方法 环境说明: MySQL 5.7.30CentOS Linux release 7.6.1810 (Core) 创建完Mysql数据库后可以查看mysql 日志获取root 用户登录密码 [rootlocalhost mysql-5.7.30]# cat /var/l…...

使用Python实现Rest API指南
在今天的数字化世界中,数据的获取、交换和使用已经成为几乎所有行业的核心部分。无论您正在为一个大型公司设计复杂的软件系统,还是只是为了个人项目尝试获得一些公开的数据,理解和利 用API——尤其是RESTful API——都是一项至关重要的技术。…...
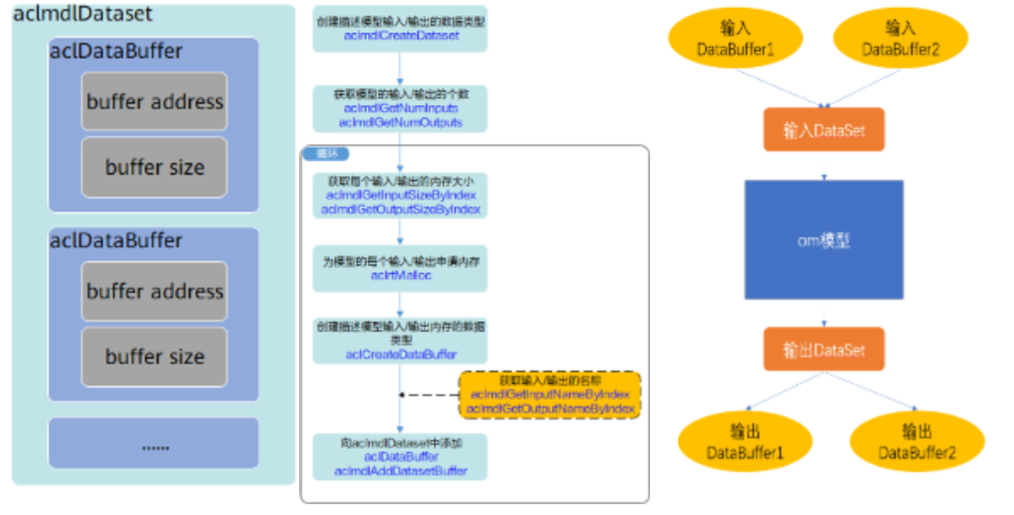
【2023 · CANN训练营第一季】进阶班 应用开发深入讲解→模型推理
1 模型离线推理 各步要解析如下: Host&Device内存管理与数据传输: Host&Device上的内存申请与释放,内存间的相互拷贝;模型加载:将离线的om文件加载到Device上;在样例的资源初始化模块中进行。模型输入输出准备∶根据禹线om的输入输出,在Device…...

单词分析问题
题目描述 小蓝正在学习一门神奇的语言,这门语言中的单词都是由小写英文字母组 成,有些单词很长,远远超过正常英文单词的长度。小蓝学了很长时间也记不住一些单词,他准备不再完全记忆这些单词,而是根据单词中哪个字母出…...

3个月出国|材料科学老师自费赴韩国访学
K老师指定韩国为访学的目标国家,希望专业匹配,尽快出国。最终我们获得了韩国庆北大学的邀请函,其学校名气、专业匹配度及导师影响力都符合K老师的要求。本案例从开始委托我们申请到最终出国,仅仅用时3个月。 K老师背景:…...

MaaS来临,SaaS进入「奇点」时刻|产业深度
大模型热度持续发酵。MaaS的到来,不仅改变了云厂商的竞争格局,SaaS行业也将迎来「奇点」时刻。未来十年,基于MaaS底座,国内SaaS甚至可能会出现Salesforce一样的巨头。 作者|思杭 编辑|皮爷 出品|产业家 大模型热度正在持续发酵。…...

课程分享:华清远见联合NXP推出i.MX8M Plus开发与实践课程,超干超实用!
课程名称: i.MX8M Plus开发与实践课程 课程介绍: i.MX8M Plus应用处理器是NXP推出的一款致力于推动机器学习(ML),机器视觉,多媒体与工业边缘物联网应用的工业人工智能芯片。拥有4个ARM Cortex-A53核心…...
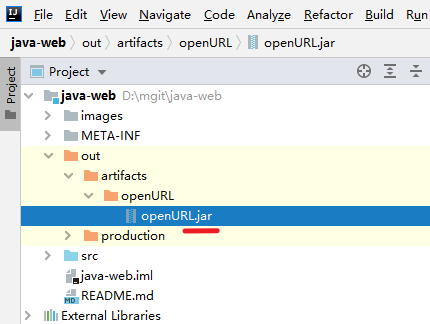
idea将java程序打包为jar
idea将java程序打包为jar 灵光一现: 用java拉起浏览器,打开指定的网络地址,省的手动打开浏览器再复制地址过去了 本文记录了使用idea将java程序打包为jar包的过程 源码地址:https://gitcode.net/qq_39339588/jar.git 文章目录 ide…...

快速掌握Redis基础知识及使用技巧
Redis 是一个高性能、基于内存的键值数据库,其主要特点是支持多种数据结构和高并发读写操作。在本文中,我们将介绍 Redis 的基本概念和使用方法,以帮助读者快速入门 Redis。 Redis 的基本概念 Redis 是一种基于内存的高性能 key-value 存储系…...
C++控制台打飞机小游戏
我终于决定还是把这个放出来。 视频在这:https://v.youku.com/v_show/id_XNDQxMTQwNDA3Mg.html 具体信息主界面上都有写。 按空格暂停,建议暂停后再升级属性。 记录最高分的文件进行了加密。 有boss(上面视频2分47秒)。 挺好…...
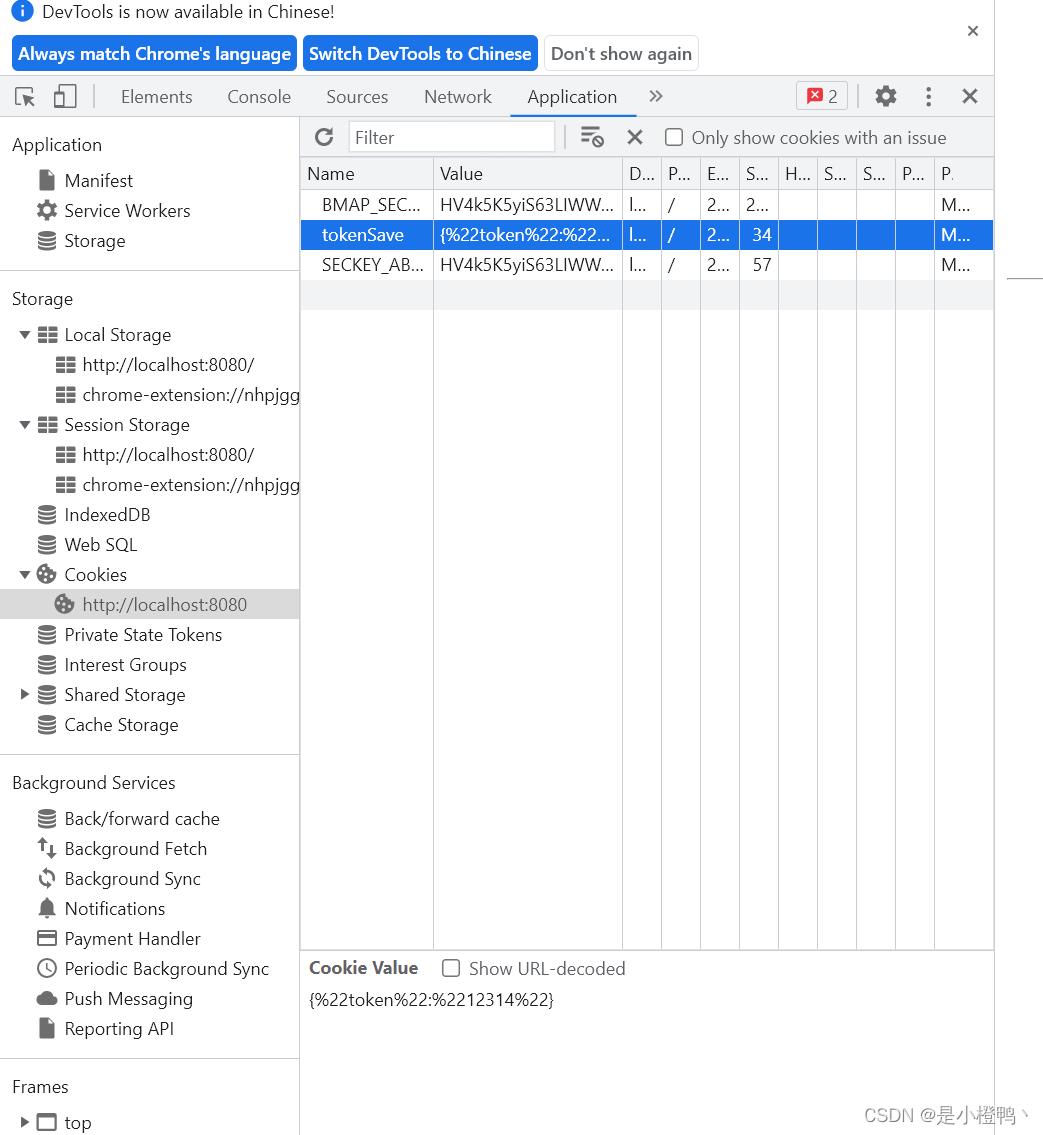
Pinna的使用以及pinna的持续化存储(两种方法)
一、简介 pinia是 vue3 新的状态管理工具,简单来说相当于之前 vuex,它去掉了 Mutations 但是也是支持 vue2 的,需要的朋友可以参考下 二、使用方法 1.安装 npm install pinia -S 2..引入 import { createPinia,PiniaPluginContext } from p…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
