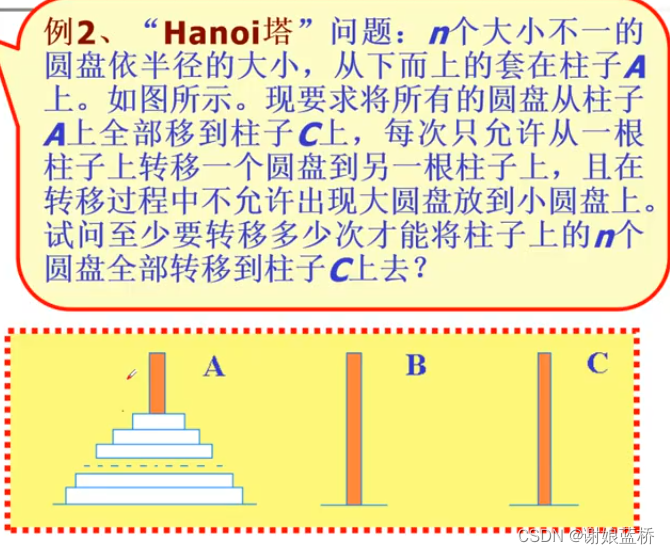
[组合数学]母函数与递推关系
文章目录
- 母函数---解决计数
- 递推关系
- 常系数线性齐次递推关系
- 常系数线性非齐次递推关系
- 汉诺塔递推关系
母函数—解决计数
普母函数—组合问题
指母函数—排列问题

f(x)= ∑ i = 1 n a i x i = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + . . . + a n x n C n 0 + C n 1 ∗ x + C n 2 ∗ x 2 + . . . + C n n ∗ x n = \sum_{i=1}^n{a_ix^i}=\\ a_0 +a_1x + a_2 x^2 + a_3x^3+...+a_nx^n\\ C_n^0+C_n^1*x+C_n^2*x^2+...+C_n^n*x^n = ∑i=1naixi=a0+a1x+a2x2+a3x3+...+anxnCn0+Cn1∗x+Cn2∗x2+...+Cnn∗xn= ( 1 + x ) n (1+x)^n (1+x)n
( 1 + x ) n = ∑ k = 0 n C n k x k = ∑ k = 0 n C n n − k x k (1+x)^n = \sum_{k=0}^nC_n^kx^k=\sum_{k=0}^nC_n^{n-k}x^k (1+x)n=∑k=0nCnkxk=∑k=0nCnn−kxk

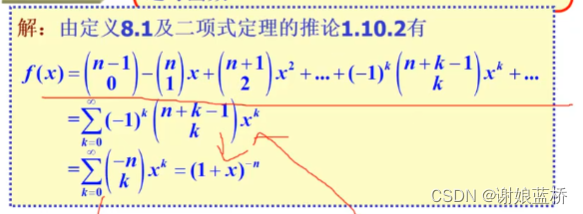
∑ k = 0 ∞ ( − 1 ) k C n + k − 1 k z k = 1 ( 1 + z ) n = ( 1 + z ) − n \sum_{k=0}^\infty (-1)^kC_{n+k-1}^{k}z^k=\frac{1}{(1+z)^n}=(1+z)^{-n} ∑k=0∞(−1)kCn+k−1kzk=(1+z)n1=(1+z)−n
( 1 + z ) α = ∑ k = 0 ∞ C α k z k (1+z)^{\alpha}=\sum_{k=0}^{\infty}C_{\alpha}^kz^k (1+z)α=∑k=0∞Cαkzk
( 1 − z ) − n = 1 ( 1 − z ) − n = ∑ k = 0 ∞ C n + k − 1 k z k 其中 ∣ z ∣ < 1 (1-z)^{-n} = \frac{1}{(1-z)^{-n}}=\sum_{k=0}^{\infty}C_{n+k-1}^{k}z^k \quad 其中|z|<1 (1−z)−n=(1−z)−n1=∑k=0∞Cn+k−1kzk其中∣z∣<1
∑ n = 1 ∞ C 2 n n x n = ( 1 − 4 x ) − 1 2 \sum_{n=1}^{\infty}C_{2n}^{n}x^n=(1-4x)^{-\frac{1}{2}} ∑n=1∞C2nnxn=(1−4x)−21
其中 C 2 n n = 2 n ! n ! ∗ n ! = 2 n ∗ n ! n ! ∗ n ! = 2 n n ! 其中 C_{2n}^n=\frac{2n!}{n!*n!}=\frac{2^n*n!}{n!*n!}=\frac{2^n}{n!} 其中C2nn=n!∗n!2n!=n!∗n!2n∗n!=n!2n
1 ( 1 + x ) = ∑ k = 0 ∞ C − 1 k z k = ∑ k = 0 ∞ ( − 1 ) k x k \frac {1}{(1+x)} = \sum_{k=0}^{\infty}C_{-1}^kz^k=\sum_{k=0}^{\infty}(-1)^kx^k (1+x)1=∑k=0∞C−1kzk=∑k=0∞(−1)kxk
1 1 − x = ∑ n = 0 ∞ x n \frac {1}{1-x}=\sum_{n=0}^{\infty}x^n 1−x1=∑n=0∞xn
1 ( 1 − x ) 2 = ∑ n = 0 ∞ ( n + 1 ) x n \frac{1}{(1-x)^2}=\sum_{n=0}^{\infty}(n+1)x^n (1−x)21=∑n=0∞(n+1)xn
2 ( 1 − x ) 3 = ∑ n = 2 ∞ n ( n − 1 ) x n − 2 \frac{2}{(1-x)^3}=\sum_{n=2}^{\infty}n(n-1)x^{n-2} (1−x)32=∑n=2∞n(n−1)xn−2
6 ( 1 − x ) 4 = ∑ n = 3 ∞ n ( n − 1 ) ( n − 2 ) x n − 3 \frac{6}{(1-x)^4}=\sum_{n=3}^{\infty}n(n-1)(n-2)x^{n-3} (1−x)46=∑n=3∞n(n−1)(n−2)xn−3
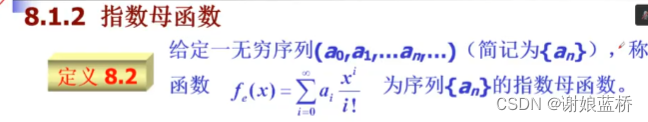
f ( x ) = a 0 + a 1 x 1 1 ! + a 2 x 2 2 ! + . . . + a n x n n ! f(x) = a_0 +a_1\frac{x_1}{1!}+a_{2}\frac{x^2}{2!}+...+a_{n}\frac{x^n}{n!} f(x)=a0+a11!x1+a22!x2+...+ann!xn
e a x = 1 + a x 1 ! + a 2 x 2 2 ! + . . . + a n x n n ! + . . . e^{ax} = 1+a\frac{x}{1!}+a^2\frac{x^2}{2!}+...+a^n\frac{x^n}{n!}+... eax=1+a1!x+a22!x2+...+ann!xn+...
e − x = 1 − x 1 ! + x 2 2 ! + . . . + ( − 1 ) n x n n ! . . . e^{-x}=1-\frac{x}{1!}+\frac{x^2}{2!}+...+(-1)^n\frac{x^n}{n!}... e−x=1−1!x+2!x2+...+(−1)nn!xn...
e x = 1 + x 1 ! + x 2 2 ! + . . . + x n n ! . . . e^{x}=1+\frac{x}{1!}+\frac{x^2}{2!}+...+\frac{x^n}{n!}... ex=1+1!x+2!x2+...+n!xn...
s i n ( x ) = x 1 + x 3 3 ! + x 2 n − 1 ( 2 n − 1 ) ! + . . . = e x − e − x 2 sin(x) = \frac{x}{1}+\frac{x^3}{3!}+\frac{x^{2n-1}}{(2n-1)!}+...=\frac{e^x - e^{-x}}{2} sin(x)=1x+3!x3+(2n−1)!x2n−1+...=2ex−e−x
c o s ( x ) = 1 + x 2 2 ! + x 4 4 ! + . . . + x 2 n 2 n ! + . . . = e − x + e x 2 cos(x)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+...+\frac{x^{2n}}{2n!}+...=\frac{e^{-x}+e^x}{2} cos(x)=1+2!x2+4!x4+...+2n!x2n+...=2e−x+ex


2m 1n 1r

组合 球相同 盒子不同 不能是空 C n − 1 m − 1 \quad C_{n-1}^{m-1} Cn−1m−1







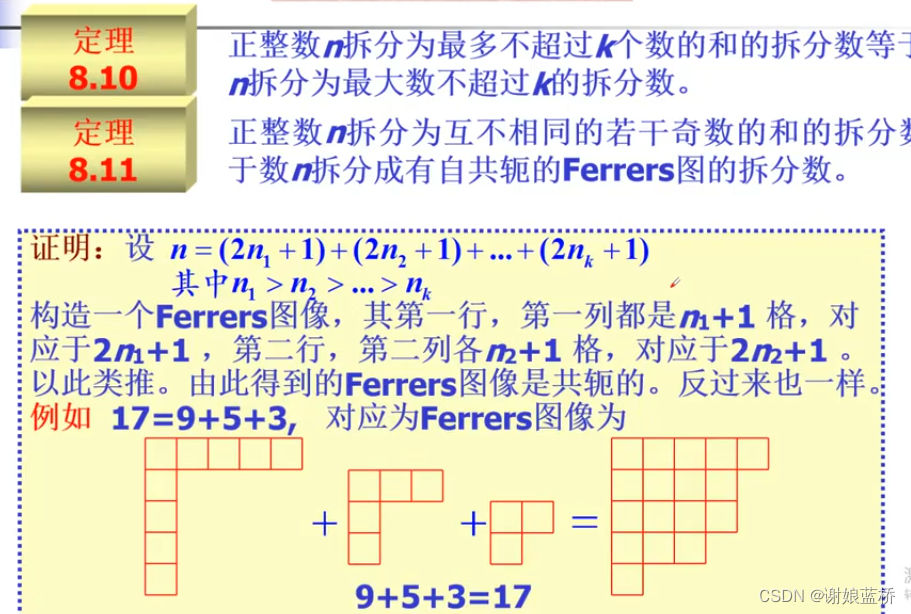
数的拆分


把正整数 拆分成 a b c 的和的方法P(n)
1 ( 1 − x a ) ( 1 − x b ) ( 1 − x c ) = ( 1 + x a + x 2 a + . . . ) ( 1 + x b + x 2 b + . . . ) ( 1 + x c + x 2 c + . . . ) \frac{1}{(1-x^a)(1-x^b)(1-x^c)}=(1+x^a+x^{2a}+...)(1+x^b+x^{2b}+...)(1+x^c+x^{2c}+...) (1−xa)(1−xb)(1−xc)1=(1+xa+x2a+...)(1+xb+x2b+...)(1+xc+x2c+...)

( 1 + x ) ( 1 + x 2 ) ( 1 + x 3 ) ( 1 + x 4 ) (1+x)(1+x^2)(1+x^3)(1+x^4) (1+x)(1+x2)(1+x3)(1+x4)

1 − x 2 = 1 + x 1 − x 1-x^2 = \frac {1+x}{1-x} 1−x2=1−x1+x
1 + x 2 = 1 − x 4 1 − x 2 1+x^2 = \frac{1-x^4}{1-x^2} 1+x2=1−x21−x4
1 − x 2 n 1 − x = 1 + x + x 2 + . . . + x 2 n − 1 \frac{1-x^{2n}}{1-x}=1+x+x^2+...+x^{2n-1} 1−x1−x2n=1+x+x2+...+x2n−1





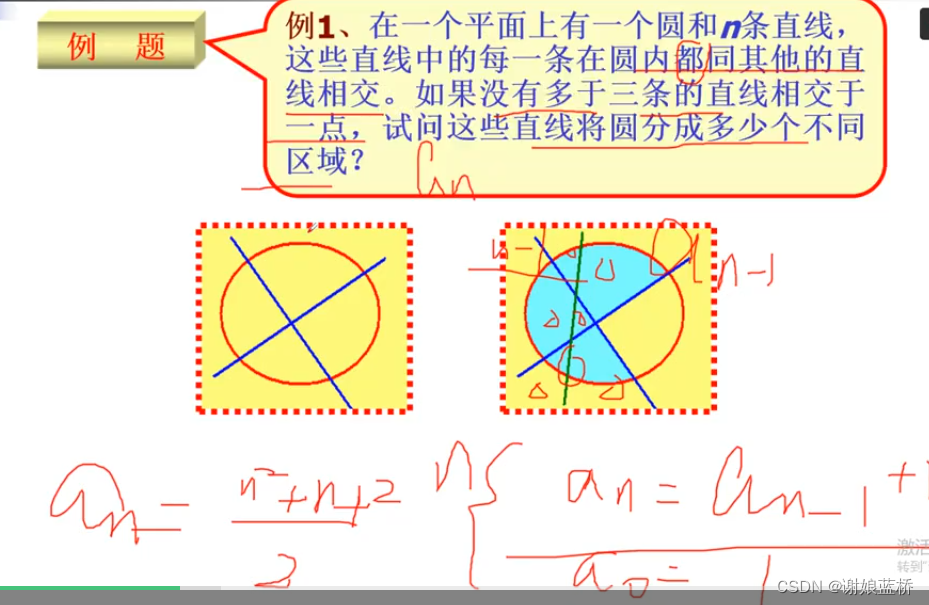
递推关系



F n − F n − 1 − F n − 2 = 0 F n − 1 − F n − 2 − F n − 3 = 0 F_n-F_{n-1}-F_{n-2}=0\\F_{n-1}-F_{n-2}-F_{n-3}=0 Fn−Fn−1−Fn−2=0Fn−1−Fn−2−Fn−3=0


C ( x ) = x n − b 1 x n − 1 − b 2 x n − 2 . . . = 0 C(x)=x^n-b_1x^{n-1}-b_2x^{n-2} ...=0 C(x)=xn−b1xn−1−b2xn−2...=0
常系数线性齐次递推关系
1.递推关系—
2.特征方程 线性齐次方程
3.求解-----特征根 q
由 a n = q n a_n=q^n an=qn是方程的解 写出通解的形式,
将初值带入即可得到递推关系


{ a n = 2 a n − 1 + a n − 2 − 2 a n − 3 ( n ≥ 3 ) a 0 = 1 , a 1 = 2 ; a 2 = 0 \begin{cases} a_n=2a_{n-1}+a_n-2-2a_{n-3} \; (n\ge 3)\\ a_0=1,a_1=2;a_2=0\\ \end{cases} {an=2an−1+an−2−2an−3(n≥3)a0=1,a1=2;a2=0
求递推关系
x 3 − 2 x 2 − x + 2 = 0 x^3-2x^2-x+2=0 x3−2x2−x+2=0
(x+1)(x-1)(x-2)=0
特征根是 -1 1 2
q 1 = 1 q 2 = − 1 q 3 = 2 q_1= 1 \quad q_2= -1 \quad q_3=2 q1=1q2=−1q3=2
通解形式为 a n = c 1 q n + c 2 q n + c 3 q n a_n=c_1q^n+c_2q^n+c_3q^n an=c1qn+c2qn+c3qn 有几个根有几项

q 最终为1,忽略掉了


x 2 − 2 x + 1 = 0 x^2-2x+1=0 x2−2x+1=0
特征根相同时, q 1 = q 2 = 1 a n = c 1 + c 2 n q_1=q_2=1 \\ a_n= c_1 +c_2n q1=q2=1an=c1+c2n

{ a n = − a n − 1 + 3 a n − 2 + 5 a n − 3 + 2 a n − 4 ( n ≥ 4 ) a 0 = 1 , a 1 = 0 , a 2 = 1 , a 3 = 2 \begin{cases} a_n=-a_{n-1}+3a_n-2+5a_{n-3}+2a_{n-4} \; (n\ge 4)\\ a_0=1,a_1=0,a_2=1,a_3=2\\ \end{cases} {an=−an−1+3an−2+5an−3+2an−4(n≥4)a0=1,a1=0,a2=1,a3=2
x 4 + x 3 − 3 x 2 − 5 x − 2 = 0 q 1 = q 2 = q 3 = − 1 , q 4 = 2 x^4+x^3-3x^2-5x-2=0\\ q1=q2=q3=-1 ,q4=2 x4+x3−3x2−5x−2=0q1=q2=q3=−1,q4=2多项式除法
a n = c 1 ( − 1 ) n + c 2 n ( − 1 ) n + c 3 n 2 ( − 1 ) n + c 4 2 n a_n=c_1(-1)^n +c_2n(-1)^n+c_3n^2(-1)^n+c_42^n an=c1(−1)n+c2n(−1)n+c3n2(−1)n+c42n
{ a 0 = c 1 + c 4 = 1 a 1 = − c 1 − c 2 − c 3 + 2 ∗ c 4 = 0 a 2 = c 1 + c 2 ∗ 2 + 4 c 3 + c 4 ∗ 4 = 1 a 3 = − c 1 − 3 c 2 − 9 c 3 + 8 c 4 = 2 \begin{cases} a_0=c_1+c_4 = 1 \\ a_1=-c_1-c_2-c_3+2*c_4=0\\ a_2 = c_1 + c_2*2+4c_3+c_4*4=1\\ a_3 = -c_1 -3c_2-9c_3+8_c4=2 \end{cases} ⎩ ⎨ ⎧a0=c1+c4=1a1=−c1−c2−c3+2∗c4=0a2=c1+c2∗2+4c3+c4∗4=1a3=−c1−3c2−9c3+8c4=2
c 1 = 42 52 , c 2 = − 29 52 , c 3 = 7 52 , c 4 = 10 52 c_1=\frac{42}{52},c_2=-\frac{29}{52},c_3=\frac{7}{52},c_4=\frac{10}{52} c1=5242,c2=−5229,c3=527,c4=5210
a n = 42 52 ( − 1 ) n − 29 52 n ( − 1 ) n + 7 52 n 2 ( − 1 ) n + 10 52 2 n a_n=\frac{42}{52}(-1)^n-\frac{29}{52}n(-1)^n+\frac{7}{52}n^2(-1)^n+\frac{10}{52}2^n an=5242(−1)n−5229n(−1)n+527n2(−1)n+52102n
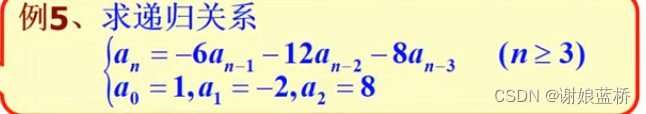
x 3 + 6 x 2 + 12 x + 8 = 0 ( x + 2 ) 3 = 0 x^3+6x^2+12x+8=0\\ (x+2)^3=0 x3+6x2+12x+8=0(x+2)3=0
( c 1 + c 2 n + c 3 n 2 = a n (c_1+c_2n+c_3n^2=a_n (c1+c2n+c3n2=an

常系数线性非齐次递推关系
1.找出递推关系
2.找出齐次递推关系,求出齐次的通解,然后求特解,从而得到递推关系
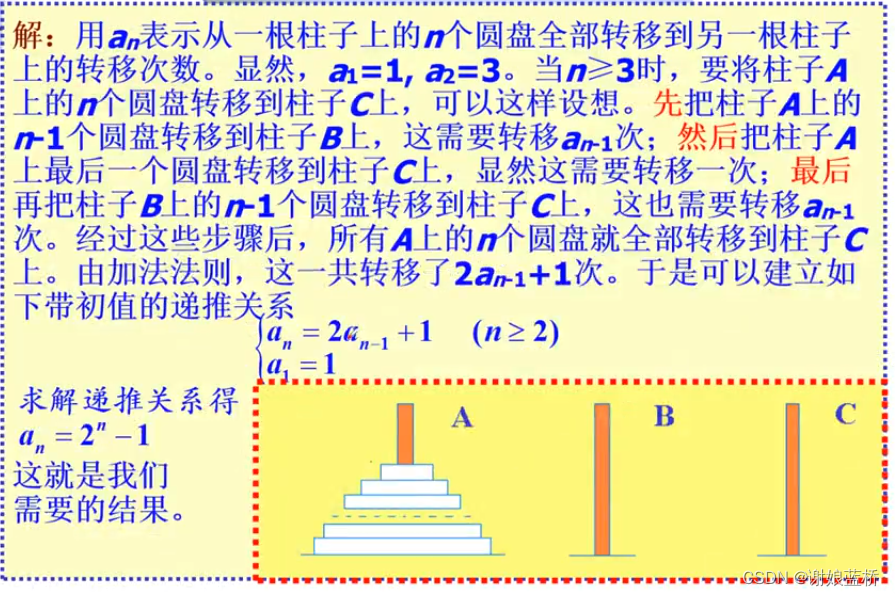
汉诺塔递推关系

求解齐次方程 a n − 2 a n − 1 = 0 a_n-2a_{n-1}=0 an−2an−1=0
特征方程 q =2
a n ∗ = c ∗ 2 n a_n^*=c *2^n an∗=c∗2n
由于f(n)=1 (上面丢掉的)

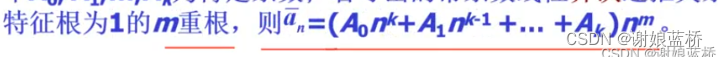
m=1 n=1 k=0 an=A
a2=3 = c1*2^n+A
A=-1


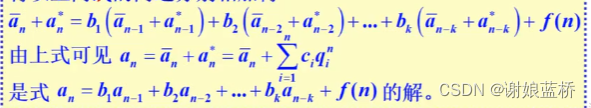
相关文章:
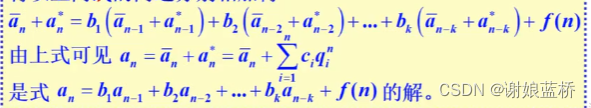
[组合数学]母函数与递推关系
文章目录 母函数---解决计数组合 球相同 盒子不同 不能是空 C n − 1 m − 1 \quad C_{n-1}^{m-1} Cn−1m−1数的拆分 递推关系常系数线性齐次递推关系常系数线性非齐次递推关系汉诺塔递推关系 母函数—解决计数 普母函数—组合问题 指母函数—排列问题 f(x) ∑ i 1 n a i…...

opencv膨胀腐蚀
OpenCV 是一个开源的计算机视觉库,它包含了许多图像处理的功能,其中膨胀和腐蚀是两种常用的形态学操作。 膨胀(Dilation):膨胀操作是将图像中的高亮区域(白色像素)扩张,从而填充低亮…...
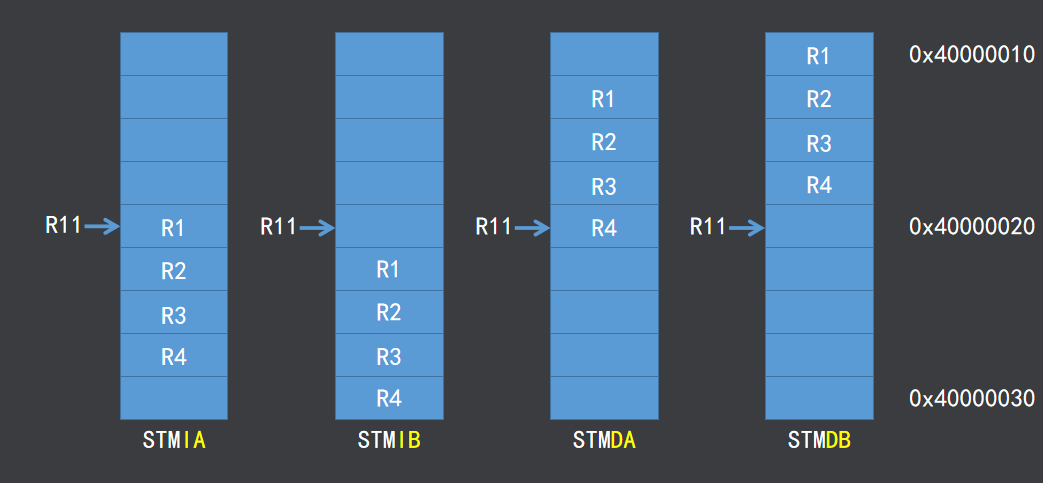
ARM的读写内存指令与栈的应用
1.基础读写指令 写内存指令:STR MOV R1, #0xFF000000 MOV R2, #0x40000000 STR R1, [R2] 将R1寄存器中的数据写入到R2指向的内存空间 需注意,此命令是将R1中的数据写给R2所指向的内存空间,而不是直接把R1的数据赋给R2,R2寄存器…...

2022年平均工资出炉,IT行业又是第一
根据5月9日国家统计局最新资料显示,2022年,全国城镇非私营单位就业人员年平均工资为114029元,比上年增长6.7%,扣除通胀后实际增长4.6%。其中,行业间的差距相当明显。根据资料显示,2022年无论是在私营单位还…...

ov2640子设备核心操作详细分析
ov2640子设备核心操作详细分析 文章目录 ov2640子设备核心操作详细分析ov2640_subdev_core_ops核心操作获取寄存器值ov2640_g_register设置寄存器值ov2640_s_registeri2c_smbus_xferi2c_imx_xferi2c_smbus_xfer_emulatedi2c_transfer__i2c_transfer 设置ov2640的电源ov2640_s_p…...

MATLAB语句实现方阵性质的验证
系列文章目录 MATLAB绘图函数的相关介绍——海底测量、二维与三维图形绘制 MATLAB求函数极限的简单介绍 matlab系统环境思维导图 文章目录 系列文章目录 1. MATLAB语句验证方阵的六个性质如下 2. 六个性质的解释如下 3. 使用随机矩阵进行验证的代码示例如下 总结 前言 …...

使用Springboot AOP进行请求接口异常监控
常用注解 Aspect 切面类 Before 前置 AfterReturning 后置 Around 环绕 AfterThrowing 异常 切入点设置 execution(public * *(..)) 定义任意公共方法的执行 execution(* set*(..)) 定义任何一个以"set"开始的方法的执行 execution(* com.sys.service.UserService…...

【云原生|Kubernetes】05-Pod的存储卷(Volume)
【云原生Kubernetes】05-Pod的存储卷(Volume) 文章目录 【云原生Kubernetes】05-Pod的存储卷(Volume)简介Volume类型解析emptyDirHostPathgcePersistentDiskNFSiscsiglusterfsceph其他volume 简介 Volume 是Pod 中能够被多个容器访问的共享目录。 Kubern…...

Python实现数据结构
文章目录 一、Python实现数据结构1.1 python实现单向链表1.2 python实现单向循环链表1.3 python实现双向链表 一、Python实现数据结构 1.1 python实现单向链表 singleLinkedList.py class SingleNode:"""the node of single link list"""def …...

esp32CAM环境安装教程---串口驱动安装
前言 (1)本人安装好arduino 的ESP32环境之后, 发现一直下载不进去程序。一直说Cannot configure port, something went wrong. Original message: PermissionError。 (2)查阅了很多资料,用了各种办法&#…...

Java中List和Array转换
文章目录 List -> Array1. 调用toArray()方法直接返回一个Object[]数组:2. 给toArray(T[])传入一个类型相同的Array,List内部自动把元素复制到传入的Array中:3. 通过List接口定义的T[] toArray(IntFunction<T[]> generator)方法&…...

如何能确定数据库中root用户的密码是什么
如果您无法确定数据库中 root 用户的密码,有几种方法可以尝试找回或重置密码: 1. 使用已知密码:如果您有之前设置的 root 用户密码,可以使用该密码进行登录。 2. 查找密码文件:在某些情况下,MariaDB 可能…...

由浅入深Netty协议设计与解析
目录 1 为什么需要协议?2 redis 协议举例3 http 协议举例4 自定义协议要素4.1 编解码器4.2 什么时候可以加 Sharable 1 为什么需要协议? TCP/IP 中消息传输基于流的方式,没有边界。 协议的目的就是划定消息的边界,制定通信双方要…...
)
iptables防火墙(1)
iptables防火墙 一、iptables概述二、netfilter/iptables 关系三、四表五链1.四表2.五链 四、规则链之间的匹配顺序五、规则链内的匹配顺序六、iptables安装与配置七、常用的控制类型八、常用的管理选项九、规则命令1.添加新规则2.查看规则列表3.设置默认策略4.删除规则5.清空规…...

第九章 Productions最佳实践 - Productions开发的最佳实践
文章目录 第九章 Productions最佳实践 - Productions开发的最佳实践Productions开发的最佳实践项目目标项目交付文档 第九章 Productions最佳实践 - Productions开发的最佳实践 Productions开发的最佳实践 本章是一个总体概述,旨在帮助团队成员为从事生产项目做好…...

RocketMQ 怎么实现的消息负载均衡以及怎么能够保证消息被顺序消费
一、RocketMQ 怎么实现的消息负载均衡 RocketMQ是一种开源的分布式消息中间件,它使用了一种称为消息负载均衡的机制来实现消息的分发和消费的负载均衡。RocketMQ的消息负载均衡主要是通过以下两个方面实现的: 消息队列分组(Message Queue G…...
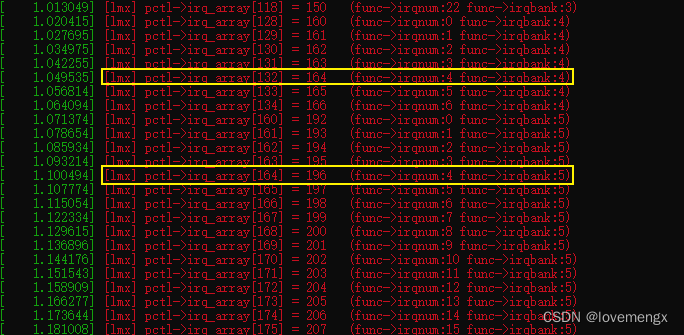
【随笔记】全志 T507 PF4 引脚无法被正常设置为中断模式的问题分析
相关信息 硬件平台:全志T507 系统版本:Android 10 / Linux 4.9.170 问题描述:PF4 无法通过标准接口设置为中断模式,而 PF1、PF2、PF3、PF5 正常可用。 分析过程 一开始以为是引脚被其它驱动占用引起,或者该引脚不具…...

人手一个 Midjourney,StableStudio 重磅开源!
人手一个 Midjourney,StableStudio 重磅开源! Stability AI 公司在上个月 19 号推出了 Alpha 版本 StableLM 大语言模型,包含了 30 亿和 70 亿参数,并且支持商用。如今他们再次推出了 AI 图像生成平台 StableStudio,这…...
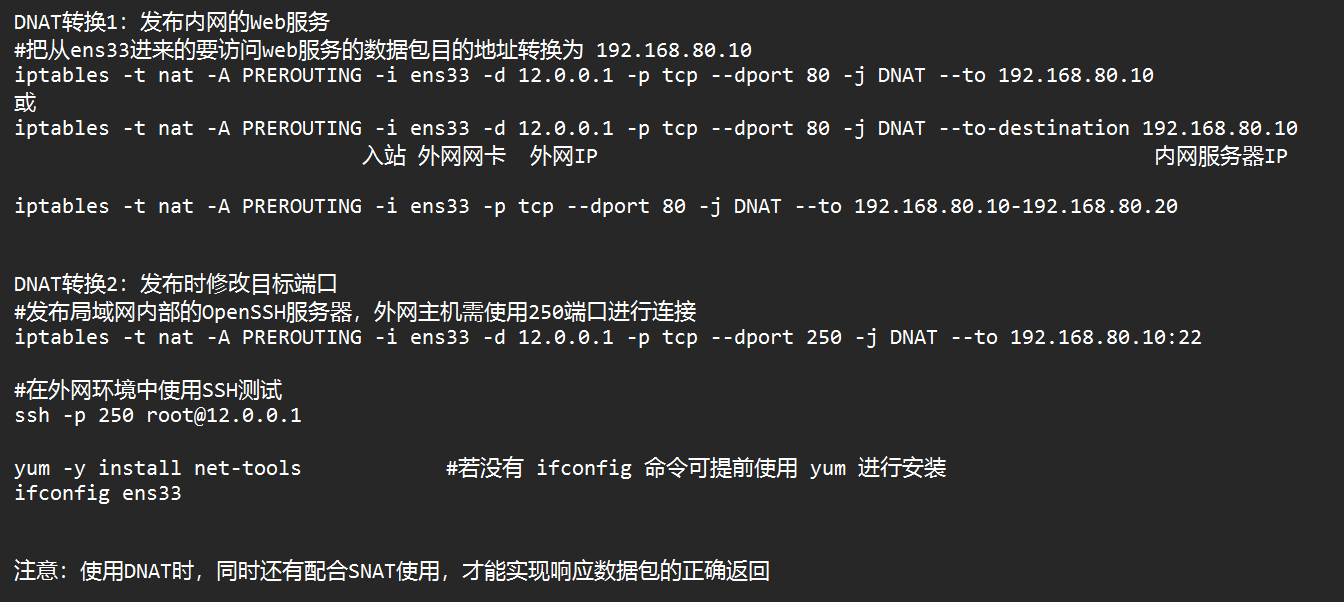
iptables防火墙(2)
iptables防火墙(2) 一、SNATSNAT应用环境SNAT原理SNAT转换前条件扩展 二、DNATDNAT应用环境DNAT原理DNAT转换前提条件扩展 三、防火墙规则的备份和还原导出(备份)所有表的规则导入(还原)规则 一、SNAT SNA…...

Windows和Kali上使用proxychains代理流量
Windows和Kali上使用proxychains代理流量 PS. 本文演示都是在kali进行的,如有出入还请联系我哦1. Linux(Debian)1.1. 检查一下是否有proxychains1.2 修改config文件 2. Linux(Debian)安装proxychians43. Windows3.1 下载3.2 配置 4. Windows下的配置5. 测试 PS. 写这…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
