【计算机系统基础3】数据的存储与运算
【计算机系统基础3】数据的存储与运算
- 3.程序调试与实践:数据存储与运算
- 3.1真值与机器数
- 3.1.1整数的编码
- 3.2数据的存储
- 3.3数组的对齐
- 3.4数据类型的转换
- 3.4.1整数之间的数据类型转换
- 3.4.2整数与浮点数之间的转换
- 3.4.3自动类型转换
- 3.5浮点数的表示和运算--IEEE 754
- 3.5.1 IEEE 754 浮点数基本格式
- 3.5.2 IEEE 754 数据按置的分类(`float` 为例)
- 3.6浮点数的表示和运算--尾数的舍入处理
3.程序调试与实践:数据存储与运算
3.1真值与机器数
真值: 数据在现实世界中的表示
机器数: 数据在计算机内部的二进制编码表示
温度:零下3.5度
习惯写法:-3.5 (数据的真值/数据的实际值)
3.1.1整数的编码
带符号整数:
char、short、int、long无符号整数:
unsigned char、unsigned short、unsigned int
-
示例代码1
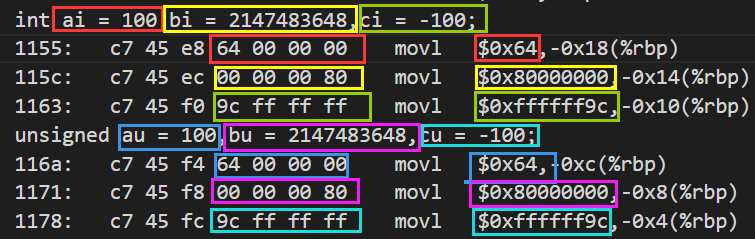
#include<stdio.h>int main() { int ai = 100,bi = 2147483648,ci = -100; // 2^31== 2147483648unsigned au = 100,bu = 2147483648,cu = -100;printf("ai=%d, bi=%d, ci=%d\n",ai,bi,ci);printf("au=%u, bu=%u, cu=%u\n",au,bu,cu);return 0; } -
示例代码1编译运行
./manu ai=100, bi=-2147483648, ci=-100 au=100, bu=2147483648, cu=4294967196问题:带符号整数
bi的输出结果值为何是负数?无符号整数
cu,赋值-个负的数据后,cu输出的结果为什么会是这个值?cu在计算机中实际存储的内容是什么?
-
反汇编查看示例1代码
相同颜色为对应值
-
问题回答
bi编码成为0xffffff9c,符号位为1,为负数,所以输出为负数。cu编码成为0xffffff9c,对于无符号整数来说,换算成十进制就是4294967196带符号整数: 补码

无符号整数: 二进制编码

3.2数据的存储
-
示例代码
#include "stdio.h" void main() {char a = 100;short b = 100;int c = 100;int d = 0x12345678;printf("a=%0xH,b=%0xH,c=%0xH,d=%0xH\n", a, b, c, d); } -
调试
(gdb) i r rsp rbp rsp 0x7ffffffedde0 0x7ffffffedde0 rbp 0x7ffffffeddf0 0x7ffffffeddf0 ...//执行完 int d = 0x12345678; (gdb) x/16xb $rsp 0x7ffffffedde0: 0xe0 0xde 0xfe 0xff 0xff 0x64 0x64 0x00 0x7ffffffedde8: 0x64 0x00 0x00 0x00 0x78 0x56 0x34 0x12变量在栈帧中的存储,因为系统是小端模式。
大端方式:最高有效字节存放在低地址单元中,
最低有效字节存放在高地址单元中。小端方式:最高有效字节存放在高地址单元中,
最低有效字节存放在低地址单元中。
3.3数组的对齐
-
示例代码
#include "stdio.h"void main() {struct record{char a;int b;short c;char d;} R[2];R[0].a = 1;R[0].b = 2;R[0].c = 3;R[0].d = 4;R[1].a = 5;R[1].b = 6;R[1].c = 7;R[1].d = 8;printf("数据存储时的边界对齐"); } -
调试
...//运行完R[1].d = 8; (gdb) x/32xb $rsp 0x7ffffffeddd0: 0x01 0x00 0x00 0x00 0x02 0x00 0x00 0x00 0x7ffffffeddd8: 0x03 0x00 0x04 0x08 0x05 0x00 0x00 0x00 0x7ffffffedde0: 0x06 0x00 0x00 0x00 0x07 0x00 0x08 0x00 0x7ffffffedde8: 0x00 0x8c 0x05 0x6b 0xb3 0xa8 0xe2 0x8c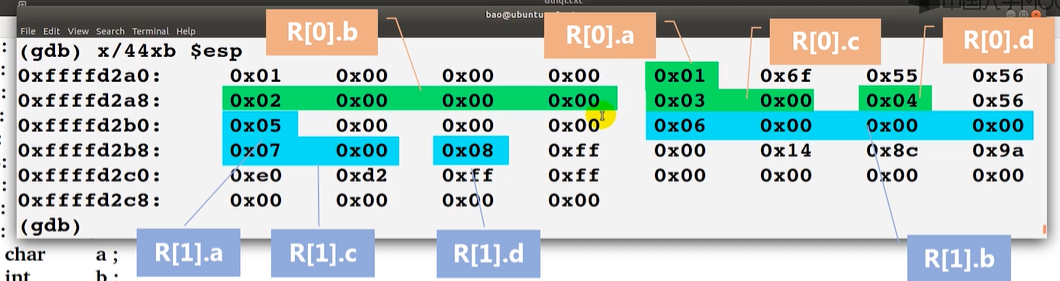


不考虑对齐方式下:数组R占用
(1+4+2+1)x2=16字节对齐方式下:数组R占用
(1+3+4+2+1+1)x2=24字节相比于不对齐,每个数组多占用 4 个字节
-
示例代码修改后
#include "stdio.h"void main() {struct record{char a;char d;short c;int b;} R[2];R[0].a = 1;R[0].b = 2;R[0].c = 3;R[0].d = 4;R[1].a = 5;R[1].b = 6;R[1].c = 7;R[1].d = 8;printf("数据存储时的边界对齐"); } -
调试
(gdb) x/20xb $rsp 0x7ffffffeddd0: 0x01 0x04 0x03 0x00 0x02 0x00 0x00 0x00 0x7ffffffeddd8: 0x05 0x08 0x07 0x00 0x06 0x00 0x00 0x00 0x7ffffffedde0: 0xe0 0xde 0xfe 0xff
3.4数据类型的转换
3.4.1整数之间的数据类型转换
机器数之间的转换
赋值语句:b = a;
-
情况一:相同宽度的两个整型数据之间的赋值

a和b的机器数相同,真值不一定相同,取决于a和b的数据类型
-
情况二:将一个短的数据类型赋值给一个长的数据类型
-

-
把
a的n位01序列复制在b的低n位,b的高m-n位由a的数据类型决定-
n位无符号整数
-

将b的高
m-n位置为0 -
n位带符号整数
-

将b的高
m-n位置为 a 的符号位
-
-
-
情况三:将一个长的数据类型赋值给一个短的数据类型

- 将
a的低m位的01序列赋值给b,丢弃a的高位部分
-
示例代码
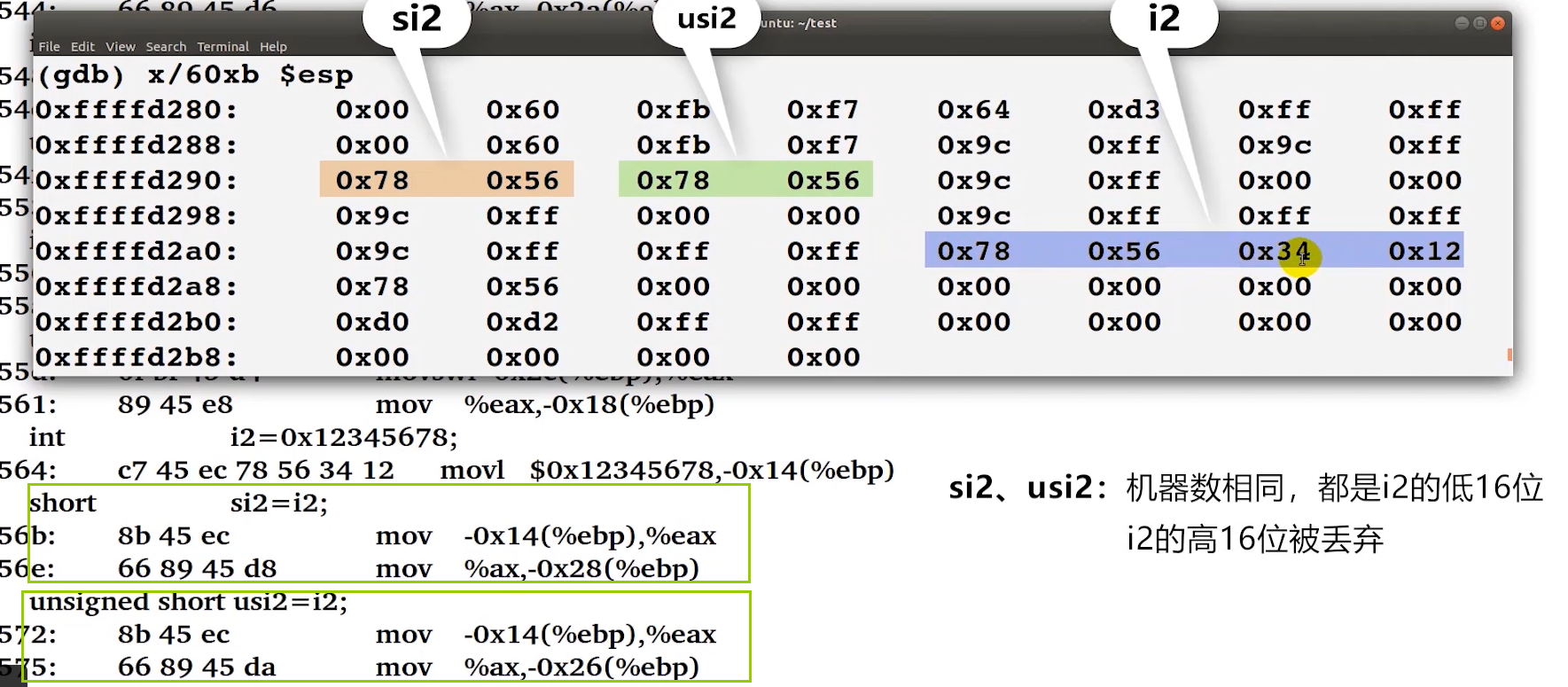
#include "stdio.h" void main() {short si = -100;unsigned short usi = si;int i = usi;unsigned ui = usi;int i1 = si;unsigned ui1 = si;int i2 = 0x12348765;short si2 = i2;unsigned short usi2 = i2;int i3 = si2;int i4 = 4294967296;printf("si=%d,usi=%u,i=%d,ui=%u,i1=%d,ui1=%u\n", si, usi, i, ui, i1, ui1);printf("i2=%d,si2=%d,usi2=%u,i3=%d,i4=%d\n", i2, si2, usi2, i3, i4); } -
调试
-
相同宽度的两个整型数据之间的赋值示例

-
零扩展代码示例
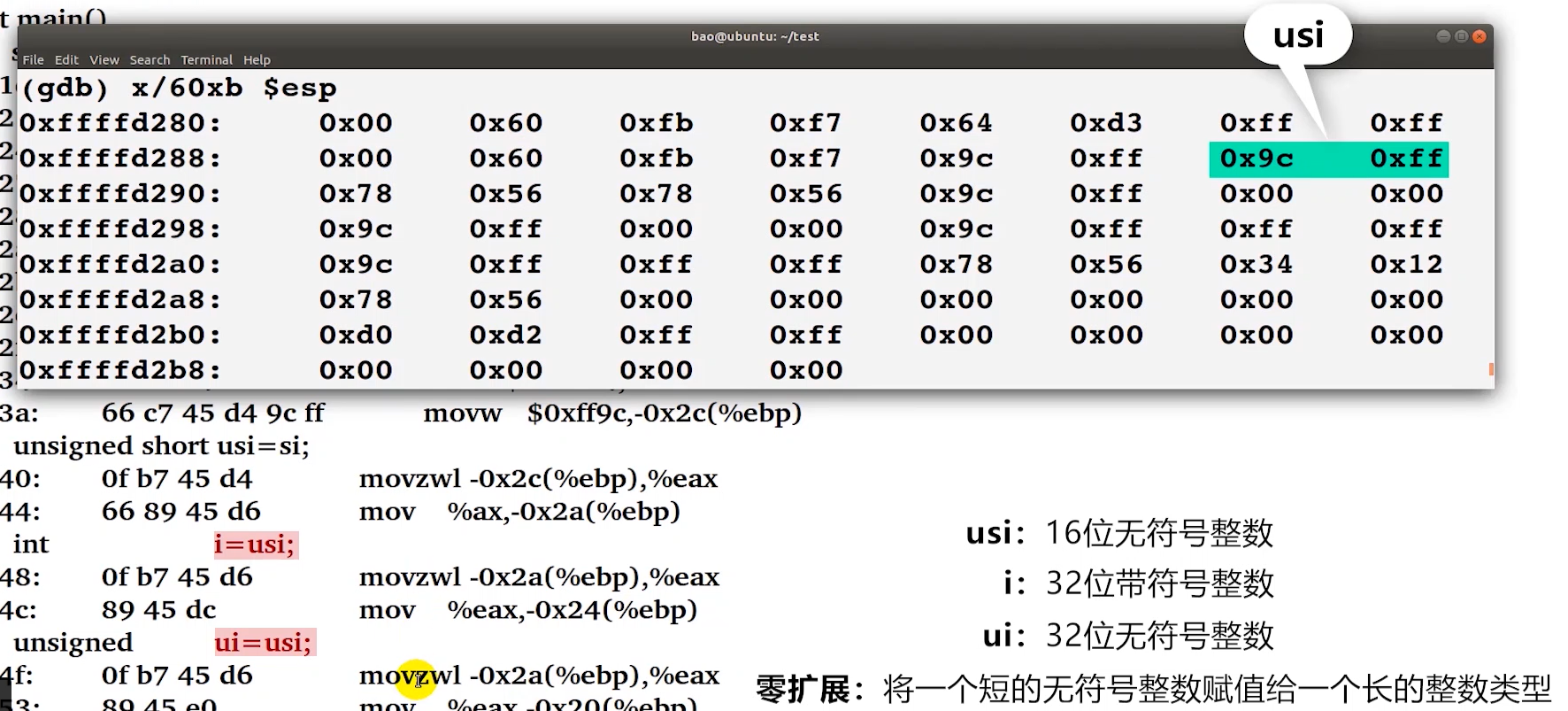
-
符号扩展示例
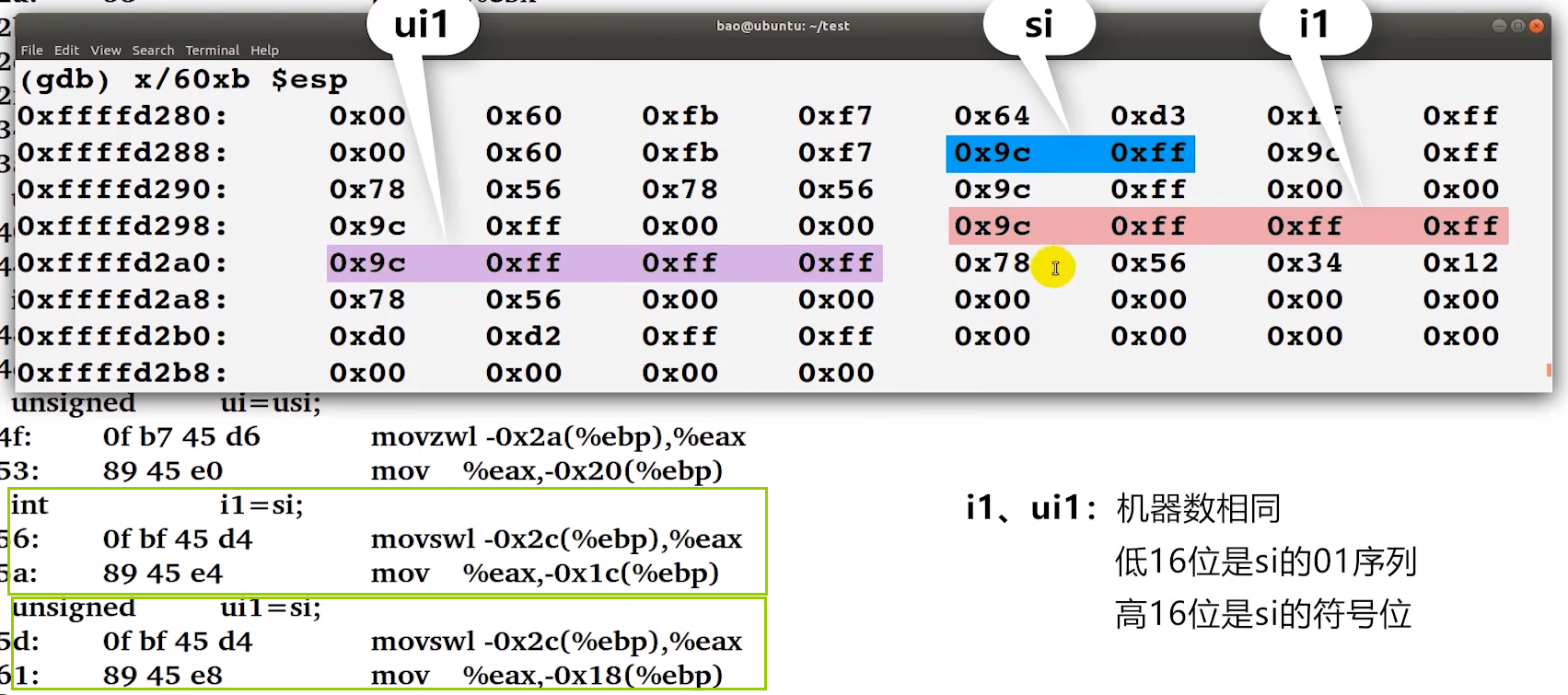
-
截断
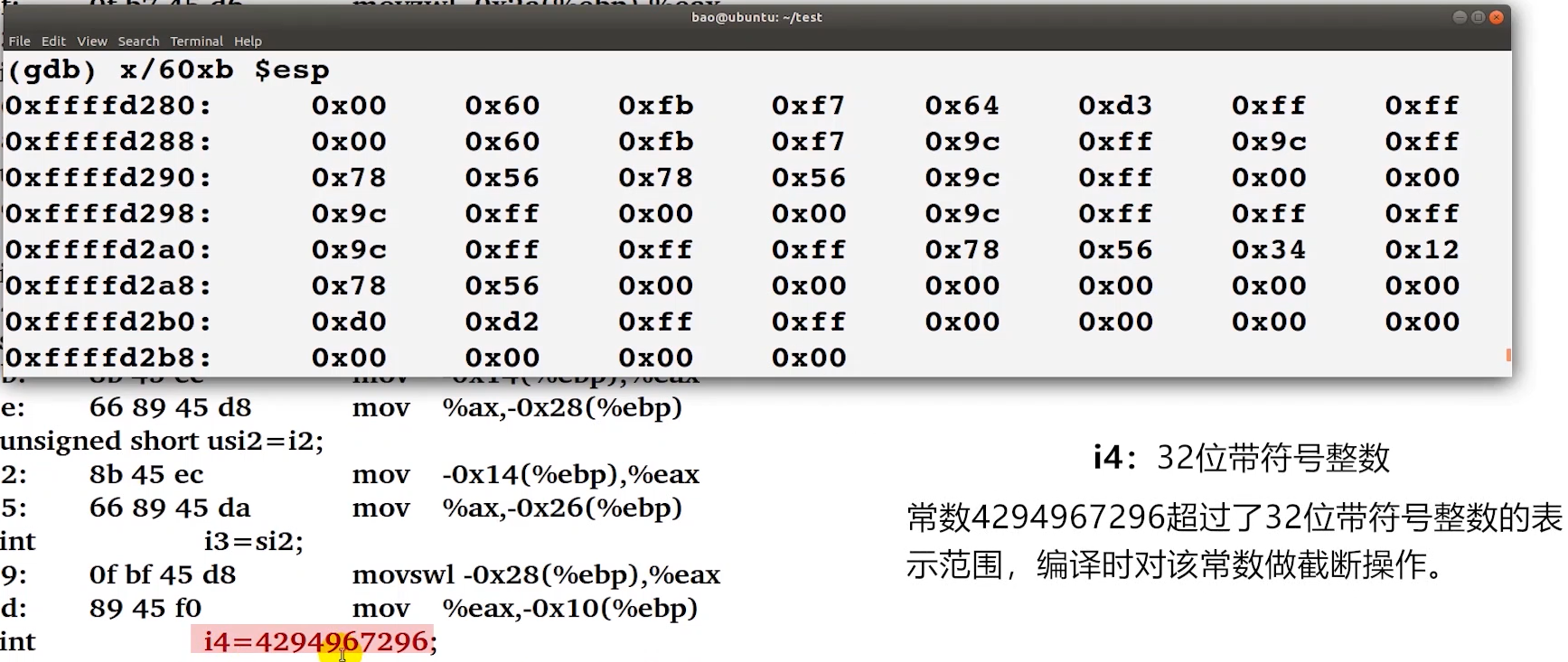
-
3.4.2整数与浮点数之间的转换
-
示例代码
#include<stdio.h> int main() {int i1=0x7fffffff,i2,itemp;float f1=0x987654321,f2,ftemp;ftemp = i1;i2 = ftemp;itemp = f1;f2 = itemp;printf("i1=%d,i2=%d,f1=%f,f2=%f\n",i1,i2,f1,f2);return 0; } -
整数到浮点数
要进行数据编码格式上的转换,而不是机器数上的直接复制。


没看太明白😕
-
浮点数到整数

3.4.3自动类型转换
-
示例代码
#include<stdio.h>int f1(unsigned int n) {int sum = 1,power = 1;int i;for(i = 0;i <= n - 1;i++){power *= 2;sum += power;}return sum; }int main() {int sum;sum = f1(0);printf("sum=%d\n",sum);return 0; } -
执行后结果:死循环

关键在于这儿的比较,
i于n - 1的比较会自动转换为无符号整型的比较,执行完n - 1后,n的数值(edx)如下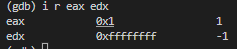
这个数在无符号整型的比较下恒成立,所以为死循环
-
修改内容
#include<stdio.h>int f1(int n)//改为整型 {int sum = 1,power = 1;int i;for(i = 0;i <= n - 1;i++) {power *= 2;sum += power;}return sum; }int main() {int sum;sum = f1(0);printf("sum=%d\n",sum);return 0; }
3.5浮点数的表示和运算–IEEE 754
3.5.1 IEEE 754 浮点数基本格式
-
float类型,32 位的单精度浮点格式
-
double类型,64 位的双精度浮点格式
3.5.2 IEEE 754 数据按置的分类(float 为例)
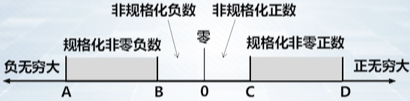
- 分类五类,下图没有体现的是无定义数
-
各类值的编码
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Utc5JczA-1684569046231)(…/软件杯-高性能分析型连接查询/image-20220627151052118.png)]
-
真值与机器数对应关系举例
-
规格化数

-
非规格化数

-
-
示例程序
#include "stdio.h" void main() {float finf1 = 4e38,finf2 = 5e38,finf3 = 6e38; //正无穷大float fninf1 = -4e38, fninf2 = -5e38, fninf3 = -6e38; //负无穷大float fzero = 0, fnzero = -fzero;// 0,-0float fnormal1 = 5.0, fnormal2 = 0.1, fnnormal1 = -5, fnnormal2 = -0.1; //规格化数float ffrac = 1e-40, fnfrac = -1e-40;//非规格化数float fnan1 = finf1 + fninf1, fnan2 = -fnan1;//无定义数float finf4 = fnormal1 / fzero; //除以0,无穷大printf("%f %f %f\n", finf1, finf2, finf3);printf("%f %f %f\n", fninf1, fninf2, fninf3);printf("%f %f\n", fzero, fnzero);printf("%f %.20f \n%f %.20f\n", fnormal1, fnormal2, fnnormal1, fnnormal2);printf("%.50f\n%.50f\n", ffrac, fnfrac);printf("%f %f\n", fnan1, fnan2);printf("%f \n", finf4); } -
输出
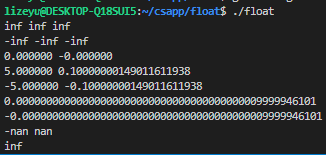
-
打印结果分析
-
第一行

-
第二行

-
第三行

-
第四行

-
第五行

-
第六行

-
第七行
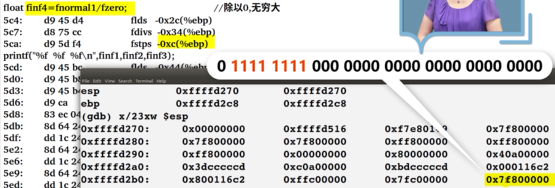
-
3.6浮点数的表示和运算–尾数的舍入处理
-
以32位单精度浮点数格式为例(就近舍入法)

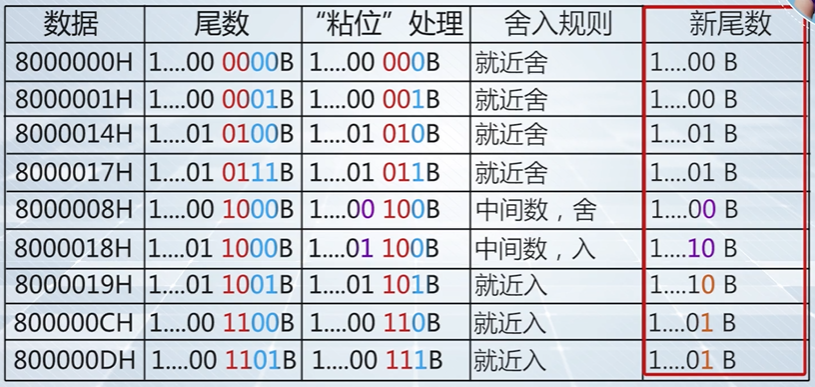
-
示例代码
#include <stdio.h>void main() {float a1 = 0x8000000, a2 = 0x8000001, a3 = 0x8000014, a4 = 0x8000017;float b1 = 0x8000019, b2 = 0x800000c, b3 = 0x800000d;float c1 = 0x8000008, c2 = 0x8000018;float g = 0.1;printf("a1=%xH,a2=%xH,a3=%xH,a4=%xH\n",(int)a1,(int)a2,(int)a3,(int)a4);printf("b1=%xH,b2=%xH,b3=%xH\n",(int)b1,(int)b2,(int)b3);printf("c1=%xH,c2=%xH\n",(int)c1,(int)c2);printf("g=%.20f",g); }; -
编译运行
./floatround a1=8000000H,a2=8000000H,a3=8000010H,a4=8000010H b1=8000020H,b2=8000010H,b3=8000010H c1=8000000H,c2=8000020H g=0.10000000149011611938a1. a2、a3、a4:输出值 ≤ 初始值, 舍操作
b1、b2、b3:输出值 > 初始值, 入操作
c1:输出值 < 初始值, 舍操作
c2:输出值 > 初始值, 入操作
g:输出值> 0.1, 0.1用机器数不可以精确表示,入操作 -
分析
-
相关文章:

【计算机系统基础3】数据的存储与运算
【计算机系统基础3】数据的存储与运算 3.程序调试与实践:数据存储与运算3.1真值与机器数3.1.1整数的编码 3.2数据的存储3.3数组的对齐3.4数据类型的转换3.4.1整数之间的数据类型转换3.4.2整数与浮点数之间的转换3.4.3自动类型转换 3.5浮点数的表示和运算--IEEE 7543…...

【算法】快速排序
目录 核心思想: 过程: 演示: 第一趟: 第二趟: 代码: 核心思想: 从待排序列中取一个元素作为中心,所有比它小或相等的元素一律放在前面, 所有比它大的元素放在后面&…...
【移动端网页布局】流式布局案例 ③ ( 实现搜索栏功能 | 伪元素选择器 | 子绝父相 | 外边距塌陷处理 | 二倍精灵图处理方案 )
文章目录 一、搜索栏样式及核心要点1、实现效果2、自动伸缩搜索栏实现3、搜索栏父容器设置4、搜索栏左右两侧的按钮盒子5、搜索栏盒子6、二倍精灵图处理方案 二、完整代码示例1、HTML 标签结构2、CSS 样式3、展示效果 一、搜索栏样式及核心要点 1、实现效果 上一篇博客中 , 完成…...
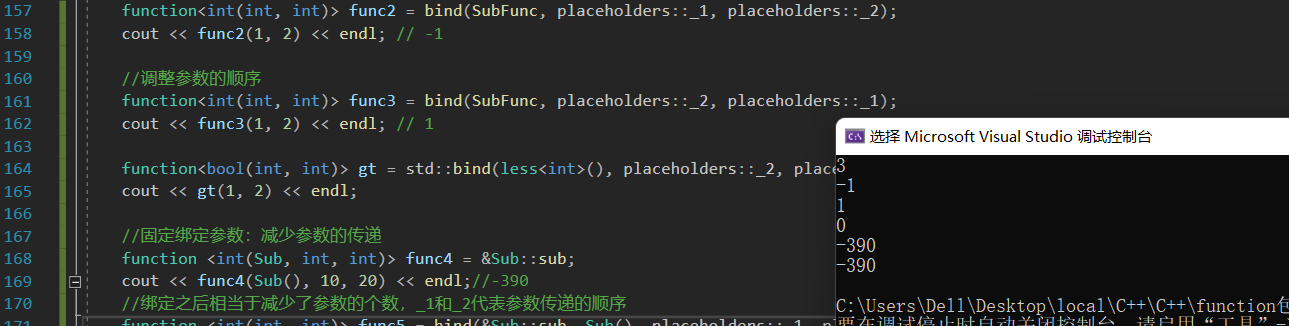
【C++修炼之路】30.可变参数模板包装器
每一个不曾起舞的日子都是对生命的辜负 C11之可变参数模板&&包装器 前言一.可变参数模板的首次登场二.参数包展开2.1 递归函数方式展开参数包2.2 逗号表达式展开参数包 三.容器的emplace方法四.包装器4.1 什么是function4.2 function包装器的作用4.3 function的实际用途…...

Linux防火墙之firewalld基础
一、firewalld概述 firewalld防火墙是Centos7系统默认的防火墙管理工具,取代了之前的iptables防火墙,也是工作在网络层,属于包过滤防火墙。 firewalld和iptables都是用来管理防火墙的工具(属于用户态)来定义防火墙的…...

GitLab CI/CD
CI/CD 简介 CI/CD 简单来说就是可以自动化编译、测试、打包我们的代码。 GitLab CICD的使用 首先需要安装gitlab-runner。 在GitLab 中,runners 是运行 CI/CD 作业的代理。我们的对代码的作业都是在runner上去执行的。我们可以在本地、服务器、等任意一个联网设…...

PHP复习资料(未完待续)
(未完待续,请持续关注此板块) 【计科三四】雪课堂PHP期末模拟题:https://ks.wjx.top/vm/tUAmjxq.aspx# 【计科一二】PHP第一章练习题 https://ks.wjx.top/vm/QnjHad4.aspx# 【计科一二】PHP第二章练习题 https://ks.wjx.top/vm/h2…...
API使用与介绍)
【python】pytorch包(第二章)API使用与介绍
1> nn.Module (用于构建模型的底层逻辑) 介绍 nn.Module 是 torch.nn 中的一个类,是pytorch中自定义网络的基类 __init__需要调用super方法,继承父类属性和方法forward方法必须实现,用来定义网络的向前计算的过程…...
)
Linux驱动基础(SR501人体感应模块)
文章目录 前言一、SR501模块介绍二、设备树编写三、驱动编写1.确定主设备号2.编写file_operations结构体3.注册file_operations结构体4.出口函数编写5.probe函数和remove函数编写6.中断编写7.测试程序编写8.全部驱动程序 总结 前言 本篇文章将给大家介绍一下SR501驱动程序的编…...
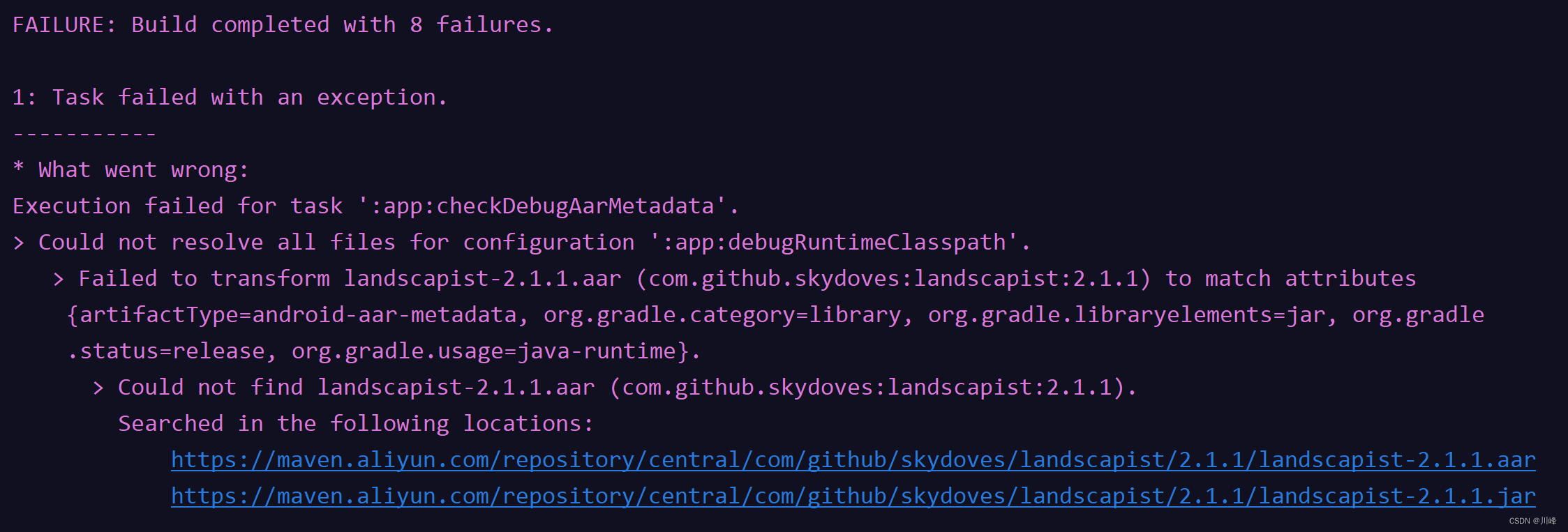
Android Studio Flamingo (火烈鸟) 升级踩坑记录
由于想要验证Compose最新的debug特性,而我目前使用的版本(Dolphin 小海豚)不支持,查看官网说明需要最新版本,所以不得已进行了一下Android Studio版本升级,过程中遇到一些问题,本文仅做记录。&a…...

【JAVA凝气】异常篇
哈喽~大家好呀,这篇来看看JAVA异常篇。 目录 一、前言 二、Exception 异常 1、Java 的非检查性异常 2、Java 检查性异常类 三、Error 错误 四、捕获异常 五、多重捕获块 六、throws/throw 关键字 七、自定义异常类 八、图书推荐 一、前言 异常是程序中的一…...

C++中的函数模板
目录 1. 什么是函数模板? 2. 如何定义函数模板? 3. 如何使用函数模板? 4. 函数模板与函数重载的区别是什么? 5. 函数模板与类模板有何异同点? 1. 什么是函数模板? - 函数模板是一种通用的函数描述&…...
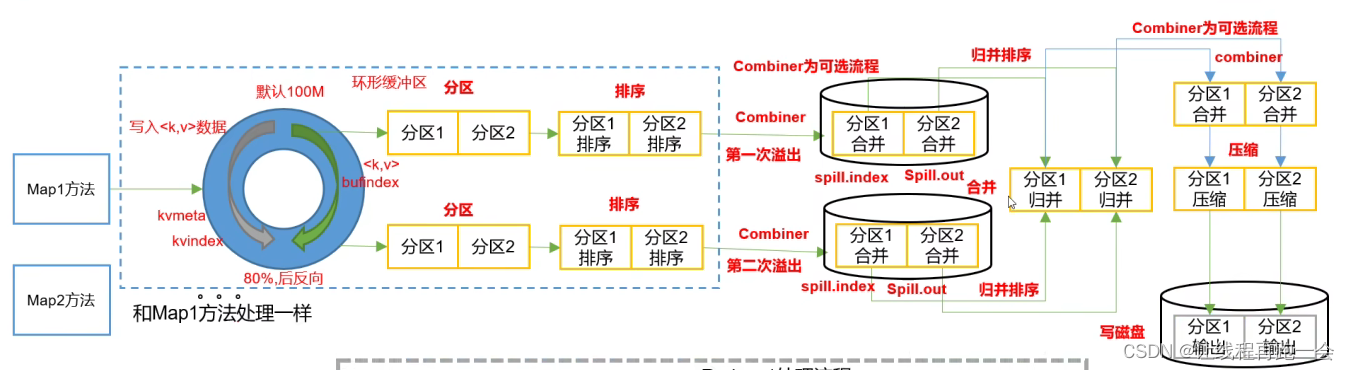
MapReduce【Shuffle-Combiner】
概述 Conbiner在MapReduce的Shuffle阶段起作用,它负责局部数据的聚合,我们可以看到,对于大数据量,如果没有Combiner,将会在磁盘上写入多个文件等待ReduceTask来拉取,但是如果有Combiner组件,我们…...
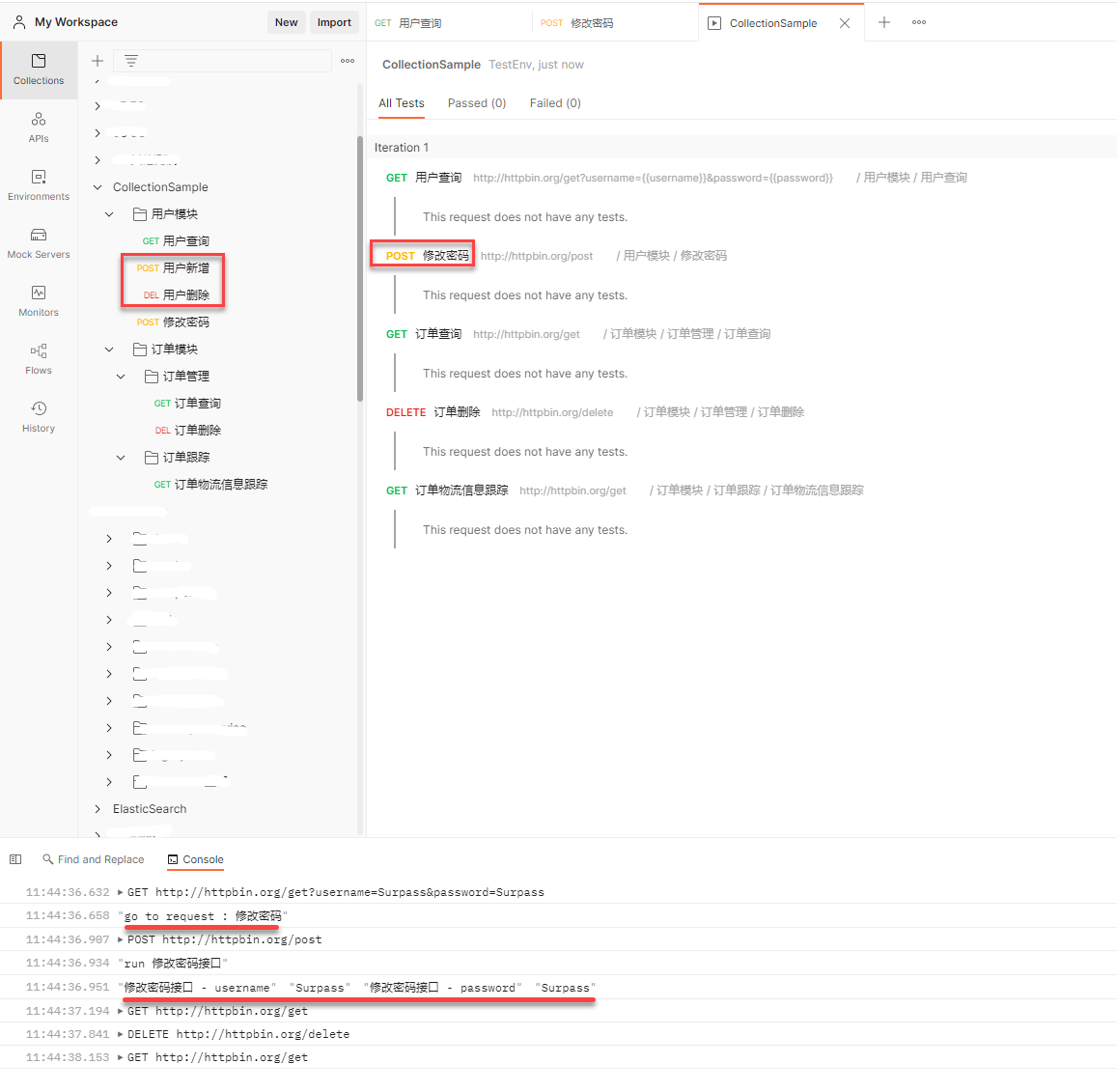
postman接口自动化测试
Postman除了前面介绍的一些功能,还有其他一些小功能在日常接口测试或许用得上。今天,我们就来盘点一下,如下所示: 1.数据驱动 想要批量执行接口用例,我们一般会将对应的接口用例放在同一个Collection中…...

历经70+场面试,我发现了大厂面试的套路都是···
今年的金三银四刚刚过去,我又想起了我在去年春招时面试了50余家,加上暑期实习面试了20余家,加起来也面试了70余场的面试场景了。 基本把国内有名的互联网公司都面了一遍,不敢说自己的面试经验很丰富,但也是不差的。 …...

可视区域兼容性问题的思考及方法封装
今日在复习可视化尺寸获取时突发奇想,为什么要在怪异模式下使用document.body.clientWidth,在标准模式下使用document.documentElement.clientWidth?以及是否在IE8及以下的版本中其中一个获取方式将返回undefined或0。 出于该问题的思考&am…...
安全工具 | CMSeeK [指纹识别]
0x00 免责声明 本文仅限于学习讨论与技术知识的分享,不得违反当地国家的法律法规。对于传播、利用文章中提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,本文作者不为此承担任何责任,一旦造成后果请自行承担…...
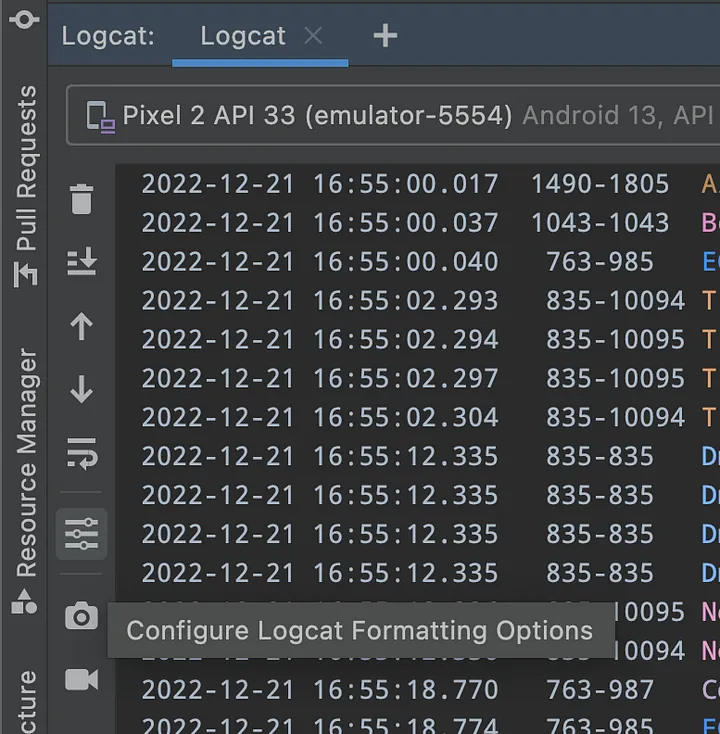
Android新logcat使用技巧
Android新logcat使用技巧 logcat新UI出现后,我常困惑于怎么过滤log,和以前的UI差异比较大,新UI界面结构如下: 这个新的 logcat 的问题是如何过滤信息并不是很明显。 获取应用的日志信息 要获取我们当前调试应用的日志信息&…...

使用Makefile笔记总结
文章目录 一、简单了解Makefile1.1 Makefile示例1.2 基本规则1.3 make是如何工作的1.4 使用变量1.5 make自动推导 二、变量2.1 变量的定义和引用2.2 变量的两种高级用法2.3 override 和 define 关键字2.4 环境变量与目标变量2.5 自动变量 三、Makefile规则3.1 通配符3.2 目标依…...

npm下载依赖项目跑不起来--解决方案
code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: vue-element-admin4.4.0 npm ERR! Found: webpack4.46.0 npm ERR! node_modules/webpack npm ERR! webpack“^4.23.0” from the root project npm ERR! npm ERR! Coul…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...


