Java前缀和算法
一.什么是前缀和算法
通俗来讲,前缀和算法就是使用一个新数组来储存原数组中前n-1个元素的和(如果新数组的当前元素的下标为n,计算当前元素的值为原数组中从0到n-1下标数组元素的和),可能这样讲起来有点抽象,我们举一个例子对其进行说明:给定一个数组nums[],我们创建一个大小为nums.length+1的求和数组sums[],对sum[]数组进行遍历:sum[i]=nums[0]+nums[1]+...+nums[i-1](相当于nums[i-1]+sum[n-1]),比如存在int[]nums={1,2,3,4},对应的前缀和数组的值为sum={0,1,3,6,10}
二.前缀和算法相对于滑动窗口具有哪些不可替代的优势及前缀和算法对算法题目的优化策略
我们在前面讲述的前缀和算法,可能很多小伙伴对其的特点也有所察觉:发现其与我们上一节讲到的滑动窗口有些类似,我们结合下面这道题目,讲讲前缀和算法对于如下这种题目而言,具有怎样的解题优势

对于滑动窗口一般的解题思路如下:如果当前窗口的元素大于预期条件的元素时,我们将窗口的左指针向右移动;如果当前窗口的元素小于预期条件的元素时,我们将窗口的右指针向右移动,扩大窗口,但是对于上面的题目中,测试用例中存在负数的情况,那么对于窗口中出现了负数这种情况,我们是该将窗口右移直到满足条件还是将窗口左移直到剔除这个负数呢?这明显超出了我们之前规定的对于使用滑动窗口的条件,这也就是滑动窗口的局限性,而根据我们对于上文中对前缀和算法的描述,前缀和算法并不规定其中的元素一定要是正数或者负数,我们只是将其中的元素进行相加,而前缀和算法对于解决这种题目可谓大显身手。
除此之外,我们讲一下前缀和算法的应用相对于我们使用暴力解法具有怎样的优化:如果不创建一个新的数组来存储前n个元素的和,那么此时我们每次求和时,都需要从头到尾将元素和全部求一遍,对于一维数组,时间复杂度达到了O(n),但是如果我们将前面元素和进行存储,每次求和只需要调用我=我们前缀和数组中的元素,时间复杂度只有O(1),大大降低了时间复杂度;同理,对于二维数组而言,他可以将O(n^2)的时间复杂度降至O(1).
三.前缀和算法的模板代码
对于前缀和算法,一般存在一维的前缀和与二维的前缀和这样两种不同的算法模板,关于前缀和算法的模板,我们使用preSum来计算数组的前缀和,preSum[i]代表着前i个前i-1个数组元素的和;对于二维数组,preSum[i][j]则代表着行为 0到i-1,列为0-j-1元素的和
一维前缀和模板
如下是一维前缀和算法的模板代码:

public int[] preSum(int[] nums) {int[] preSum = new int[nums.length+1];for (int i = 1; i < =nums.length; ++i) {preSum[i] = preSum[i - 1] + nums[i-1];}return preSum;}二维前缀和模板
如下是二维前缀和的算法模板:对于二维的前缀和模板,是对一维前缀和模板的扩展,但在本质上是完全一致的,我们来描述有关二维数组的前缀和的模板:

我们给出这样一个图示: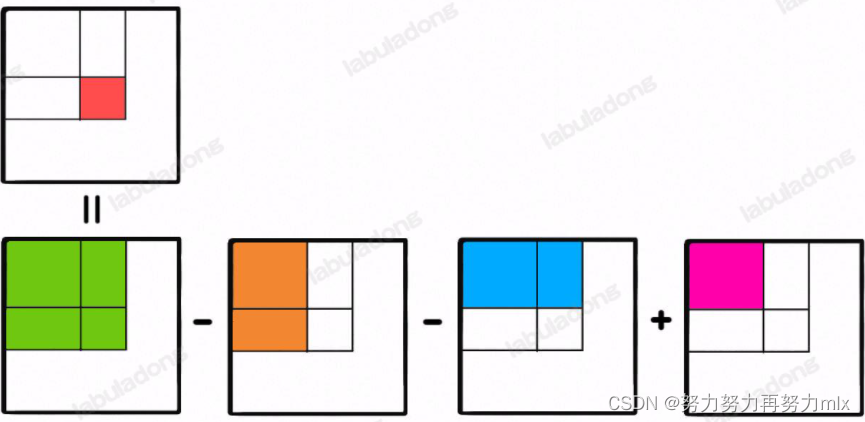
对于二维数组的前缀和而言,表达式可以表述为这样:
每一个二维数组中的单位元素,相等于绿-澄-蓝+粉,我们同样给出一个二维数组,presum[nums.length+1][nums[0].length+1],presum[n][n]则代表0-n-1行,0-n-1列的数据总和 、
其模板表达式如下:
class NumMatrix {// 定义:preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和private int[][] preSum;public NumMatrix(int[][] matrix) {int m = matrix.length, n = matrix[0].length;if (m == 0 || n == 0) return;// 构造前缀和矩阵preSum = new int[m + 1][n + 1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 计算每个矩阵 [0, 0, i, j] 的元素和preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];}}}// 计算子矩阵 [x1, y1, x2, y2] 的元素和public int sumRegion(int x1, int y1, int x2, int y2) {// 目标矩阵之和由四个相邻矩阵运算获得return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];}
}除了完全的一维和二维的前缀和算法之外,前缀和算法的题目通常会与hash等数据结构组合出题
四.关于前缀和算法的经典题目练习
1.区域和检索 - 数组不可变力扣
力扣题目描述

解题思路
这是一个完全意义上的前缀和算法的题目,或者说这是一个书写前缀和算法模板的题目,对于这道题,我们直接使用我们前面使用的前缀和算法的模板即可:创建nums.length+1长度的presum[],对于presum[n],存储的是前n-1个元素的和,每次求和时直接使用presum中的元素即可。
实例代码
我们给出实例代码:
class Solution {public int subarraySum(int[] nums, int k) {//单纯使用前缀和,无法判别从哪里进行区分,这时我们需要将符合条件的数值直接存入map,再次需要时直接拿来使用即可int count=0;//记录最终的结果int pre=0;//记录前缀和//创建mapHashMap<Integer,Integer>map=new HashMap<>();//如果是pre-target=0,代表从0开始刚好满足条件要求map.put(0,1);for(int i=0;i<nums.length;++i){pre+=nums[i];if(map.containsKey(pre-k)){count+=map.get(pre-k);}//将当前pre加入map.put(pre,map.getOrDefault(pre,0)+1);}return count;}
}class NumArray {//本题使用前缀和算法,将使劲复杂度从O(n)降至O(1)private int[]preNums;public NumArray(int[] nums) {preNums=new int[nums.length+1];//循环时创建前缀和for(int i=1;i<preNums.length;++i){preNums[i]=preNums[i-1]+nums[i-1];}}public int sumRange(int left, int right) {return preNums[right+1]-preNums[left];}
}2.和为 k 的子数组 力扣
题目描述

解题思路
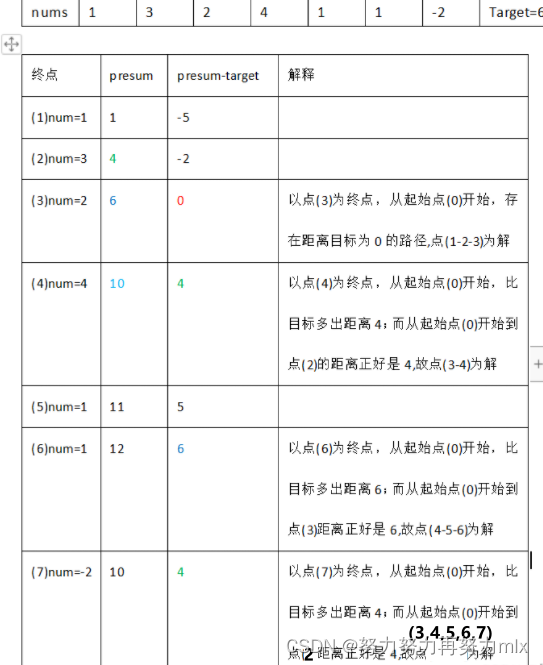
这道题就是对我们一维数组前缀和算法的扩展了,它不仅仅使用简单的前缀和数组进行存储数组的前缀和,他同样需要使用hash表进行元素的记录和存储,这是一道前缀和数组和哈希表进行融合的题目,具体的解题思路如下:我们对于这道题目而言,难点在于对于简单的前缀和数组而言,我们无法判断从哪个地方进行断开(无法判断从那个地方作为起点,哪个地方作为终点是符合条件的),因为我们在此基础上使用哈希表,哈希表中存储的是当前元素为基准的前缀和与target之间的差距,如果差距为0(恰好满足)或者当前差距等于其前面元素的前缀和(如果前面元素的前缀和为4,此时前缀和-target=4 :前缀和比我们需要的和的值大4,刚好与前面的值进行抵消),这种也是符合条件的。
图示如下:
实例代码
我们给出实例代码
class Solution {public int subarraySum(int[] nums, int k) {//单纯使用前缀和,无法判别从哪里进行区分,这时我们需要将符合条件的数值直接存入map,再次需要时直接拿来使用即可int count=0;//记录最终的结果int pre=0;//记录前缀和//创建mapHashMap<Integer,Integer>map=new HashMap<>();//如果是pre-target=0,代表从0开始刚好满足条件要求map.put(0,1);for(int i=0;i<nums.length;++i){pre+=nums[i];if(map.containsKey(pre-k)){count+=map.get(pre-k);}//将当前pre加入map.put(pre,map.getOrDefault(pre,0)+1);}return count;}
}3.二维子矩阵的和力扣
题目描述

解题思路
这道题正是我们上面讲述的关于二维数组求前缀和的典型例题,我们在上面模板的基础上进行思路的讲解:对于红框内的元素和,等于绿框元素-蓝框-红框+黑框(其中蓝框和红框中也有黑框的部分,但是被颜色覆盖了),在此之前,我们首先要将元素进行初始化,初始化的过程相当于对元素进行分割的逆过程:单位元素加上两边的元素再减去重复的元素


实例代码
class NumMatrix {//创建二维的数组和private int[][]preNums;public NumMatrix(int[][] matrix) {preNums=new int[matrix.length+1][matrix[0].length+1];//创建并遍历for(int i=1;i<preNums.length;++i){for(int j=1;j<preNums[0].length;++j){preNums[i][j]=preNums[i][j-1]+preNums[i-1][j]-preNums[i-1][j-1]+matrix[i-1][j-1];}}}public int sumRegion(int row1, int col1, int row2, int col2) {return preNums[row2+1][col2+1]-preNums[row2+1][col1]-preNums[row1][col2+1]+preNums[row1][col1];}
}4.除自身以外数组的乘积力扣
题目描述

解题思路
这道题目的解题思路相对而言比较巧妙,它将前缀和拓展为前缀积,而除了本身元素之外的其他元素的和,则恰好符合前缀积中premul[i]*lastmul[i]的定义,所以直接定义前缀后缀积进行元素的相乘即可
实例代码
class Solution {public int[] productExceptSelf(int[] nums) {//解题思路:通过前缀积和后缀积进行相乘,最终的结果就是除了nums[i]之外的相乘结果,需要注意的是:需要对前后缀积的含义进行一定的改变//定义前缀积int[]pre=new int[nums.length];//定义后缀积int[]last=new int[nums.length];//初始化并相乘pre[0]=1;for(int i=1;i<nums.length;++i){pre[i]=nums[i-1]*pre[i-1];}last[nums.length-1]=1;for(int i=nums.length-2;i>=0;--i){last[i]=last[i+1]*nums[i+1];}int[]res=new int[nums.length];//进行最后的结果返回for(int i=0;i<nums.length;++i){res[i]=pre[i]*last[i];}return res;}
}相关文章:

Java前缀和算法
一.什么是前缀和算法 通俗来讲,前缀和算法就是使用一个新数组来储存原数组中前n-1个元素的和(如果新数组的当前元素的下标为n,计算当前元素的值为原数组中从0到n-1下标数组元素的和),可能这样讲起来有点抽象࿰…...

pico 的两个双核相关函数的延时问题
pico高级API函数中, multicore_fifo_pop_timeout_us 和 multicore_fifo_push_timeout_us 的延时参数, 如修改为500微秒以上时,其延时似乎远远超过设定值,其反馈速度似乎被主核的交互所左右 ,而修改为200以下时&#x…...

Doxygen源码分析: QCString类依赖的qstr系列C函数浅析
2023-05-20 17:02:21 ChrisZZ imzhuofoxmailcom Hompage https://github.com/zchrissirhcz 文章目录 1. doxygen 版本2. QCString 类简介3. qstr 系列函数浅析qmemmove()qsnprintfqstrdup()qstrfree()qstrlen()qstrcpy()qstrncpy()qisempty()qstrcmp()qstrncmp()qisspace()qstr…...
)
华为OD机试之一种字符串压缩表示的解压(Java源码)
一种字符串压缩表示的解压 题目描述 有一种简易压缩算法:针对全部由小写英文字母组成的字符串,将其中连续超过两个相同字母的部分压缩为连续个数加该字母,其他部分保持原样不变。 例如:字符串“aaabbccccd”经过压缩成为字符串“…...

Microsoft Project Online部署方案
目录 一、前言 二、Microsoft Project Online简介 三、Microsoft Project Online的优势 1、云端部署 2、多设备支持...

飞浆AI studio人工智能课程学习(3)-在具体场景下优化Prompt
文章目录 在具体场景下优化Prompt营销场景办公效率场景日常生活场景海报背景图生成办公效率场景预设Prompt 生活场景中日常学习Prompt: 给写完的代码做文档 将优质Prompt模板化Prompt 1:Prompt 1:Prompt 2步骤文本过长而导致遗失信息的示例修改后 特殊示例 如何提升安全性主要目…...

企业工程行业管理系统源码-专业的工程管理软件-提供一站式服务
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示1…...

Ehcache 整合Spring 使用页面、对象缓存
Ehcache在很多项目中都出现过,用法也比较简单。一般的加些配置就可以了,而且Ehcache可以对页面、对象、数据进行缓存,同时支持集群/分布式缓存。如果整合Spring、Hibernate也非常的简单,Spring对Ehcache的支持也非常好。EHCache支…...

Spring Cloud中的服务路由与负载均衡
Spring Cloud中的服务路由与负载均衡 一、服务路由1. 服务发现2. 服务注册3. 服务消费4. 服务提供5. 服务路由实现 二、负载均衡1. 负载均衡的概念2. 负载均衡算法3. 负载均衡实现4. 负载均衡策略5. 使用Spring Cloud实现负载均衡 三、服务路由与负载均衡的集成1. 集成背景2. 集…...
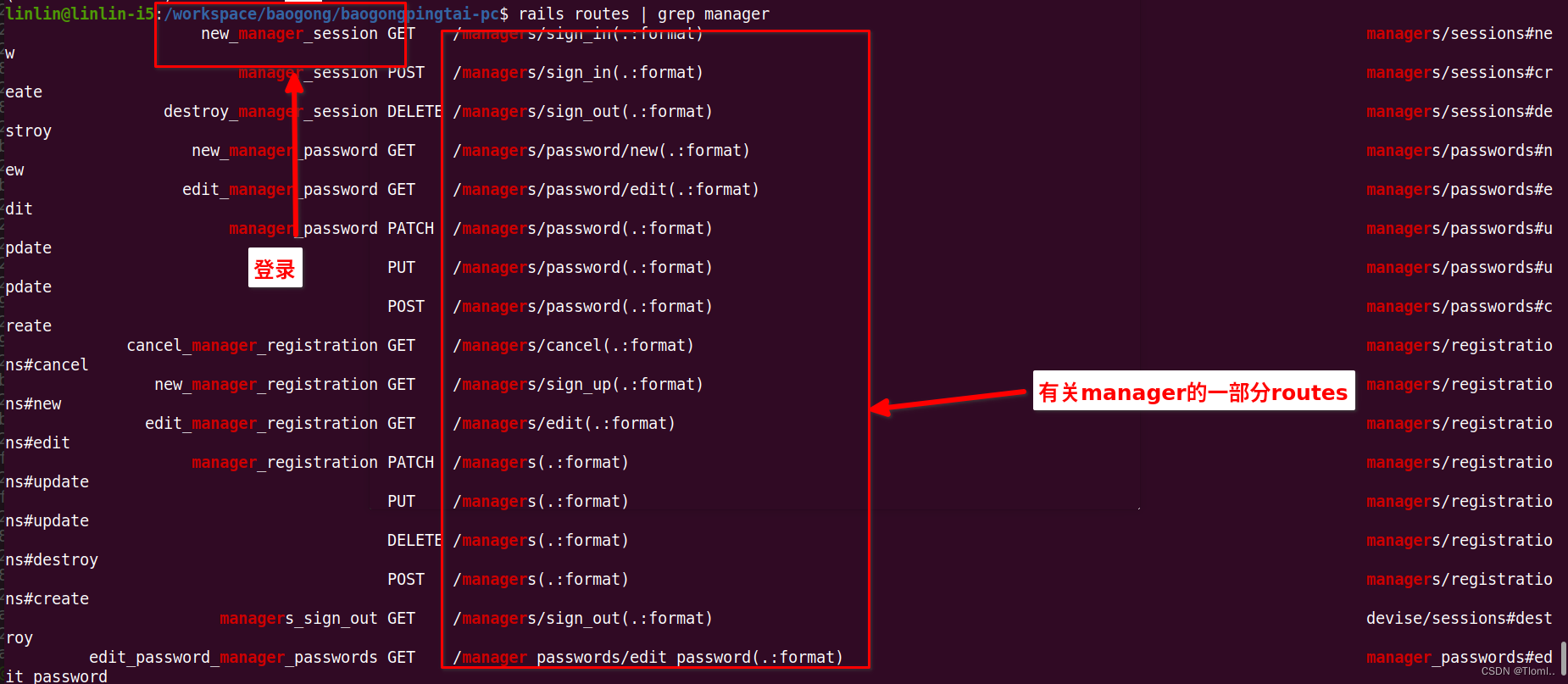
rails routes的使用
Rails routes 是用于确定应该将请求发送到哪个控制器和操作的一种机制。在 Rails 应用程序中,可以通过定义路由来映射 URL 到控制器操作。可以使用 rails routes 命令查看当前应用程序中定义的所有路由。 以下是一些常见的用法: 查看所有路由ÿ…...

Linux基础内容(21)—— 进程消息队列和信号量
Linux基础内容(20)—— 共享内存_哈里沃克的博客-CSDN博客 目录 1.消息队列 1.定义 2.操作 2.信号量 1.定义 2.细节 3.延申 4.操作 3.IPC的特点共性 1.消息队列 1.定义 定义:是操作系统提供的内核级队列 2.操作 msgget:…...
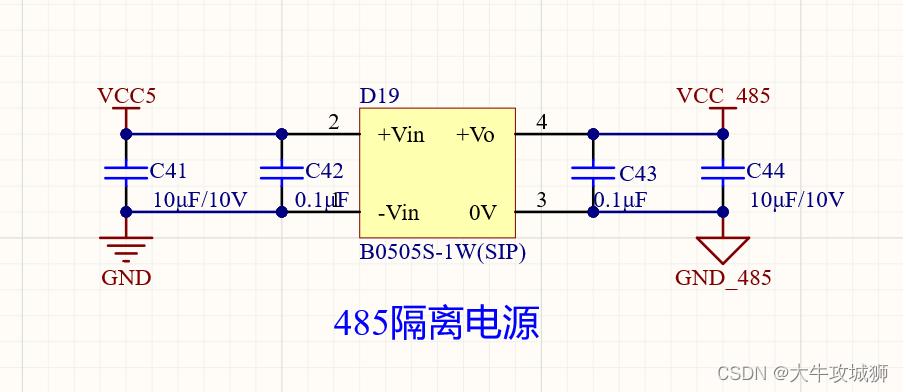
STM32实现基于RS485的简单的Modbus协议
背景 我这里用STM32实现,其实可以搬移到其他MCU,之前有项目使用STM32实现Modbus协议 这个场景比较正常,很多时候都能碰到 这里主要是Modbus和变频器通信 最常见的是使用Modbus实现传感器数据的采集,我记得之前用过一些传感器都…...
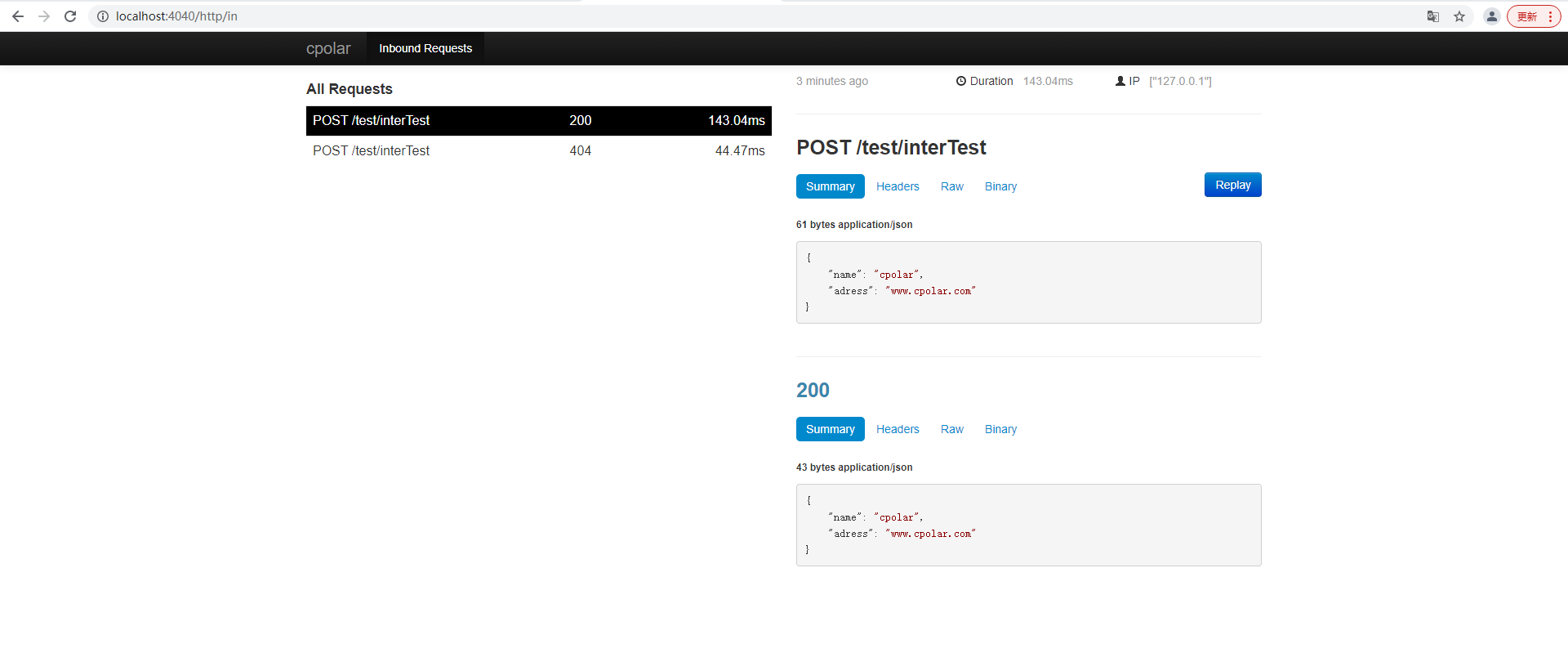
springboot服务端接口公网远程调试 - 实现HTTP服务监听【端口映射】
文章目录 前言1. 本地环境搭建1.1 环境参数1.2 搭建springboot服务项目 2. 内网穿透2.1 安装配置cpolar内网穿透2.1.1 windows系统2.1.2 linux系统 2.2 创建隧道映射本地端口2.3 测试公网地址 3. 固定公网地址3.1 保留一个二级子域名3.2 配置二级子域名3.2 测试使用固定公网地址…...
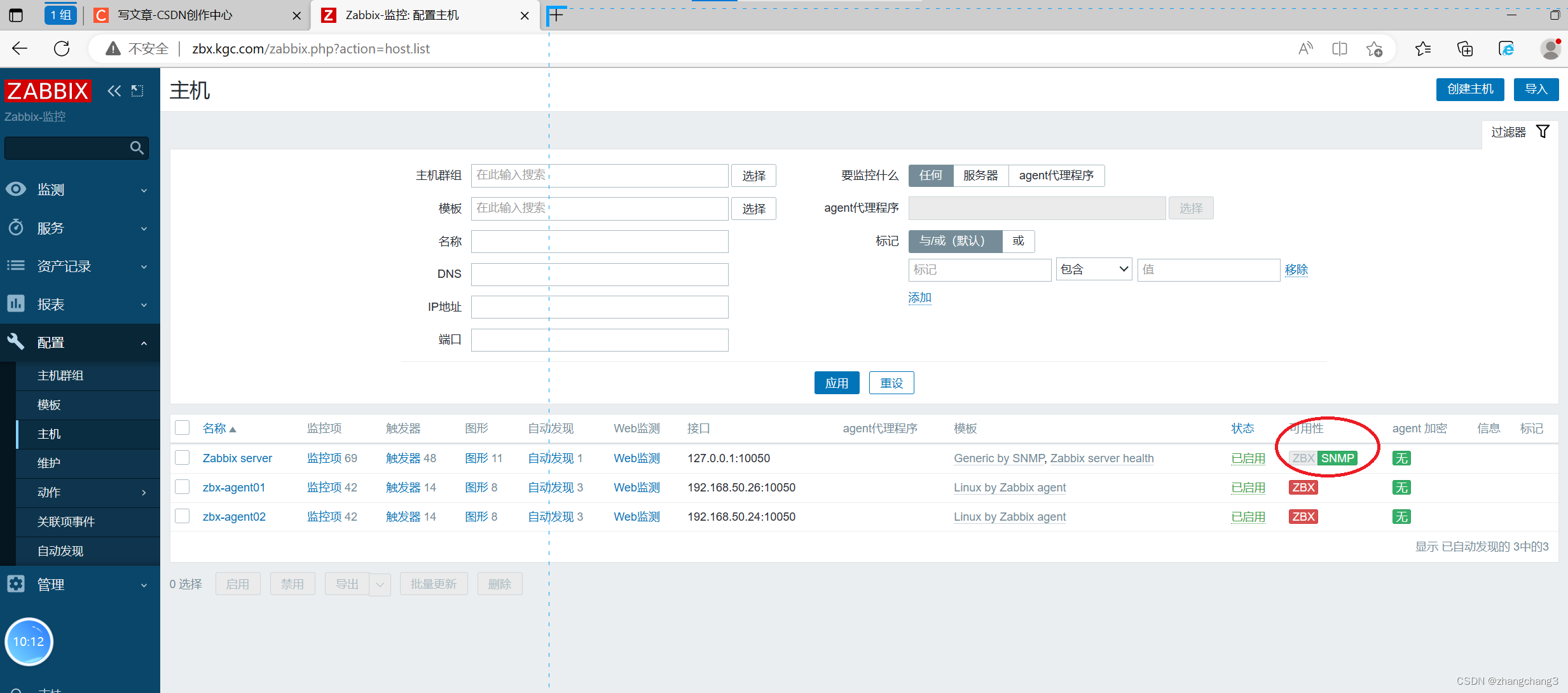
zabbix监控之javasnmp自定义监控
1、客户端开启 java jmxremote 远程监控功能 上传 tomcat 软件包到 /opt 目录中 cd /opt tar zxvf apache-tomcat-9.0.16.tar.gz mv apache-tomcat-9.0.16 /usr/local/tomcat #配置 java jmxremote 远程监控功能 vim /usr/local/tomcat/bin/catalina.sh ...... #位置在 cygw…...
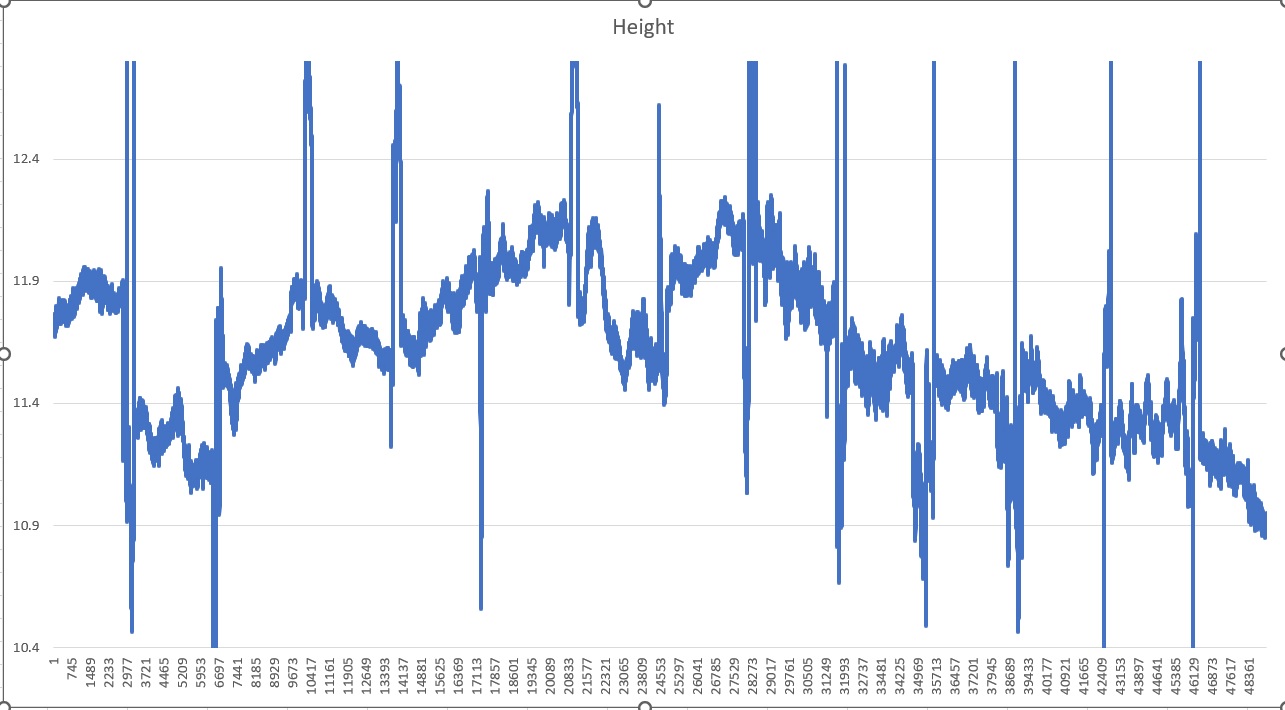
Inertial Explorer处理pospac数据总结
Inertial Explorer处理pospac数据的过程包括:1)从pospac提取出gps数据和imu数据;2)gps数据转成rinex格式;3)imu数据转成imr格式;4)IE对gps数据进行PPP解算;5)紧耦合融合解…...

tps和qps的区别是什么?怎么理解
区别:QPS指的是“每秒查询率”;而TPS指的是“事务数/秒”。理解:Tps即每秒处理事务数,对于一个页面的一次访问,形成一个Tps;而一次页面请求,可能产生多次对服务器的请求,服务器对这些…...

【Java系列】深入解析枚举类型
序言 即便平凡的日子仿佛毫无波澜,但在某个特定的时刻,执着的努力便会显现出它的价值和意义。 希望这篇文章能让你不仅有一定的收获,而且可以愉快的学习,如果有什么建议,都可以留言和我交流 问题 思考一下这寄个问题&a…...
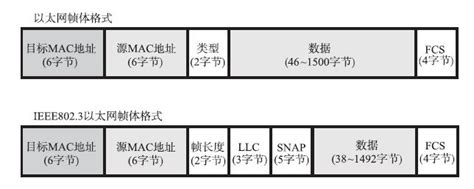
网络原理(五):IP 协议
目录 认识IP 地址 子网掩码 作用 动态分配IP 地址 NAT 机制 认识MAC地址 MAC地址如何工作 网络设备和相关技术 集线器:转发所有端口 交换机:MAC地址转换表转发 主机&路由器:ARP缓存表ARP寻址 路由器:路由NAPT 数…...
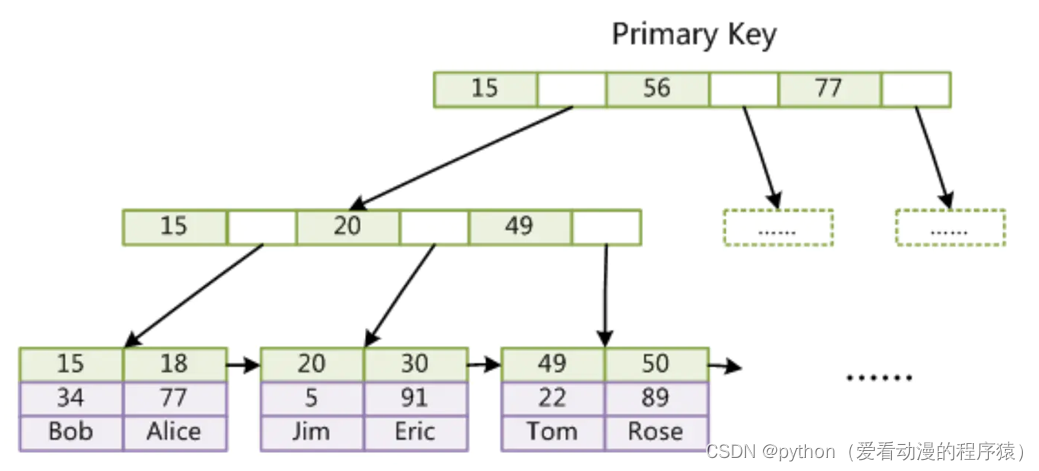
MySQL---空间索引、验证索引、索引特点、索引原理
1. 空间索引 MySQL在5.7之后的版本支持了空间索引,而且支持OpenGIS几何数据模型 空间索引是对空间数据类型的字段建立的索引,MYSQL中的空间数据类型有4种,分别是: 类型 含义 说明 Geometry 空间数据 任何一种空间类型 Poi…...
选择合适的 MQTT 云服务:一文了解 EMQX Cloud Serverless、Dedicated 与 BYOC 版本
引言 EMQX Cloud 是基于 EMQX Enterprise 构建的一款全托管云原生 MQTT 消息服务。为了满足不同客户的需求,EMQX Cloud 提供了三种版本供客户选择:Serverless 版、专有版和 BYOC 版。 本文将简要介绍这三个版本的核心区别,并通过三个用户故…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
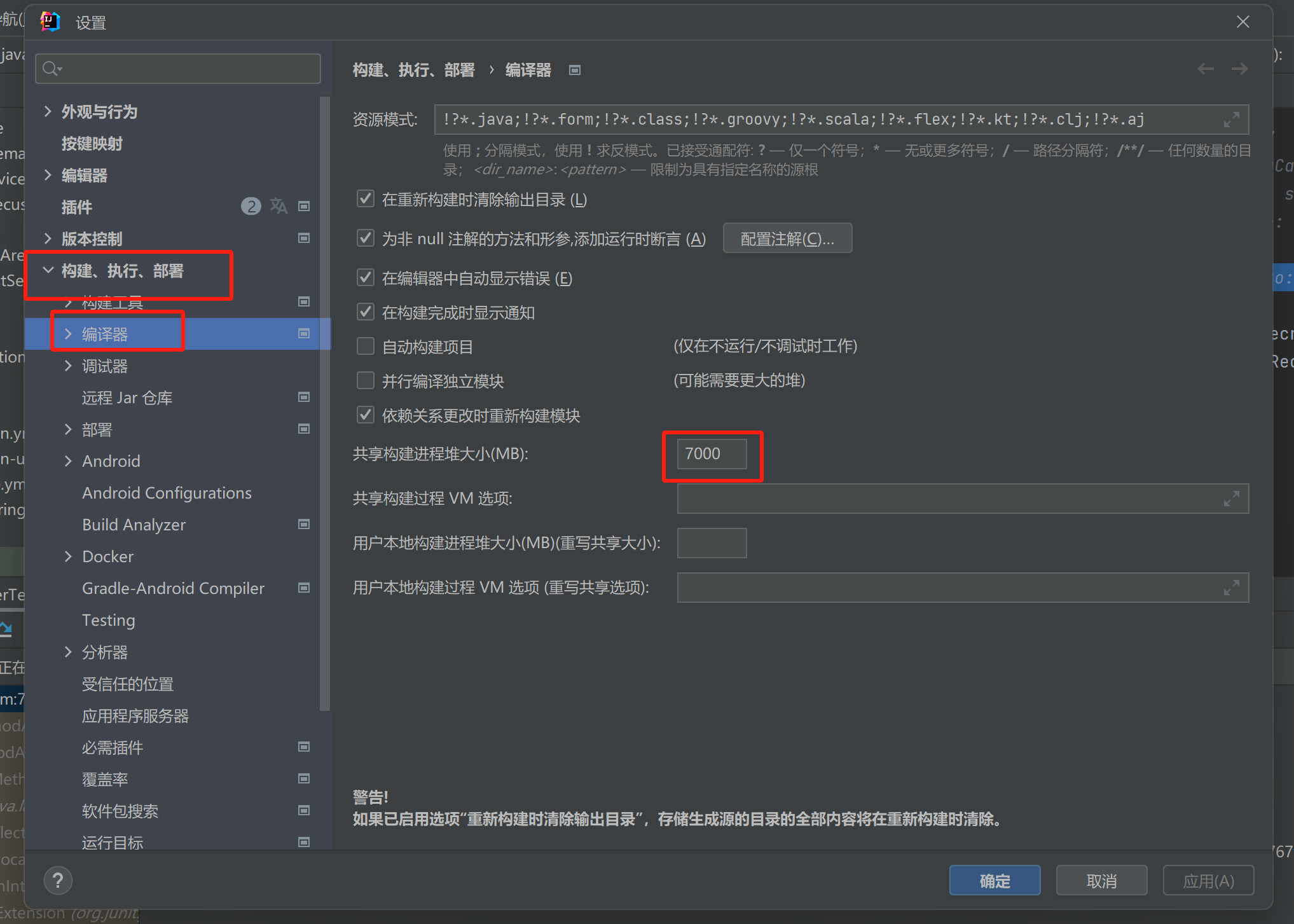
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...