CodeForces.1806A .平面移动.[简单][判断可达范围][找步数规律]
题目描述:

题目解读:
给定移动规则以及起始点,终点;分析终点是否可达,可达则输出最小步数。
解题思路:
首先要判定是否可达。画图可知,对于题目给定的移动规则,只能到达起始点(a,b)的第一象限和第二象限的上半部分。
因此对于输入的终点(c,d),构建判断语句:如果(c,d)在(a,b)的三四象限,即 d>b,不可达。如果(c,d)在(a,b)的第二象限下半部分,即 c>a && d>=b && c-a>d-b 时,也不可达。
其余可达的点计算最小路径。题目给定的移动方式是向左平移或者向右对角线移动。
我的思路是先走右对角到达终点同一高度(如果终点和起点y坐标相同则省略该步),然后左移即可。(这个思路是经过计算的,即使终点在起点的第一象限,先到右对角线再左移 和 先向左移然后通过·右对角线不断靠近,所需步数是一样的。)
从(a,b)到(c,d),先走右对角线,到达(a+d-b,d),然后向左移动到(c,d)即可。
到达(a+d-b,d)需要d-b步,移动到(c,d)需a+d-b-c步,共需要d-b+a+d-b-c。
代码实现:
//判断能否按题目要求进行移动,能的话给出最小步数
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>void Solve() {int a,b,c,d;scanf("%d%d%d%d", &a,&b,&c,&d);if (b>d || (c>a && d>=b && c-a>d-b)){printf("%d\n",-1);}else printf("%d\n", (d-b)+ (a+d-b)-c );return;
}int main() {int t;scanf("%d", &t);while (t--) Solve();return 0;
}遇到的错误:求解移动步数的时候容易卡壳。
相关文章:

CodeForces.1806A .平面移动.[简单][判断可达范围][找步数规律]
题目描述: 题目解读: 给定移动规则以及起始点,终点;分析终点是否可达,可达则输出最小步数。 解题思路: 首先要判定是否可达。画图可知,对于题目给定的移动规则,只能到达起始点(a,b…...
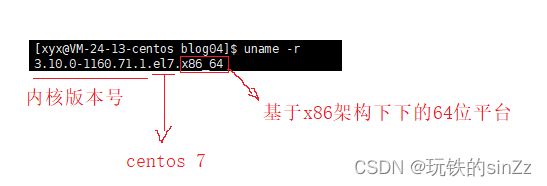
Linux系统编程学习 NO.4 ——基础指令学习、操作系统时间的概念、文件压缩包的概念
1.时间相关的概念以及指令 1.1.时间相关的指令 1.1.1.date指令 date可以指定时间显示的格式:date 指定格式 选项 %H:小时 %M:分钟 %S:秒数 %Y:年份 %m:月份 %d:日 %F:相当于%Y-%m-%d %X:相当…...

leecode 数据库:601. 体育馆的人流量
导入数据: Create table If Not Exists Stadium (id int, visit_date DATE NULL, people int); Truncate table Stadium; insert into Stadium (id, visit_date, people) values (1, 2017-01-01, 10); insert into Stadium (id, visit_date, people) values (2, 20…...
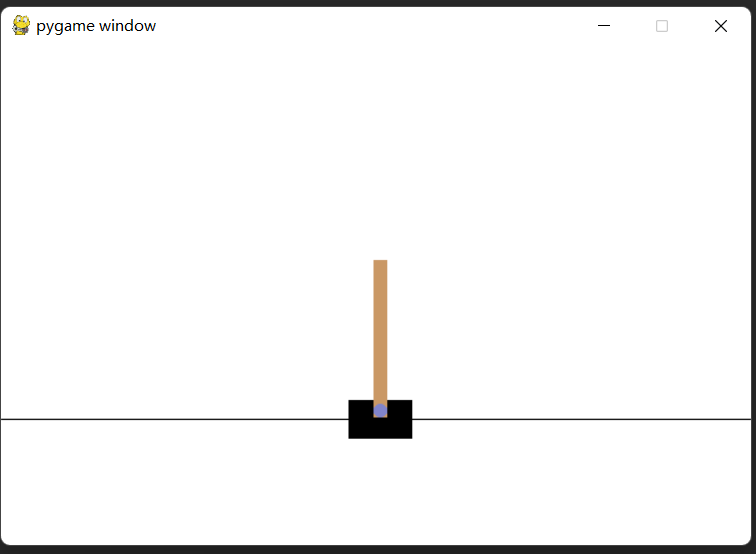
gym不渲染画面的解决方案(gym版本号0.26.2)
确认gym版本号 我安装了新版gym,版本号是0.26.2,不渲染画面的原因是,新版gym需要在初始化env时新增一个实参render_mode‘human’,并且不需要主动调用render方法,官方文档入门教程如下 import gym import numpy as n…...
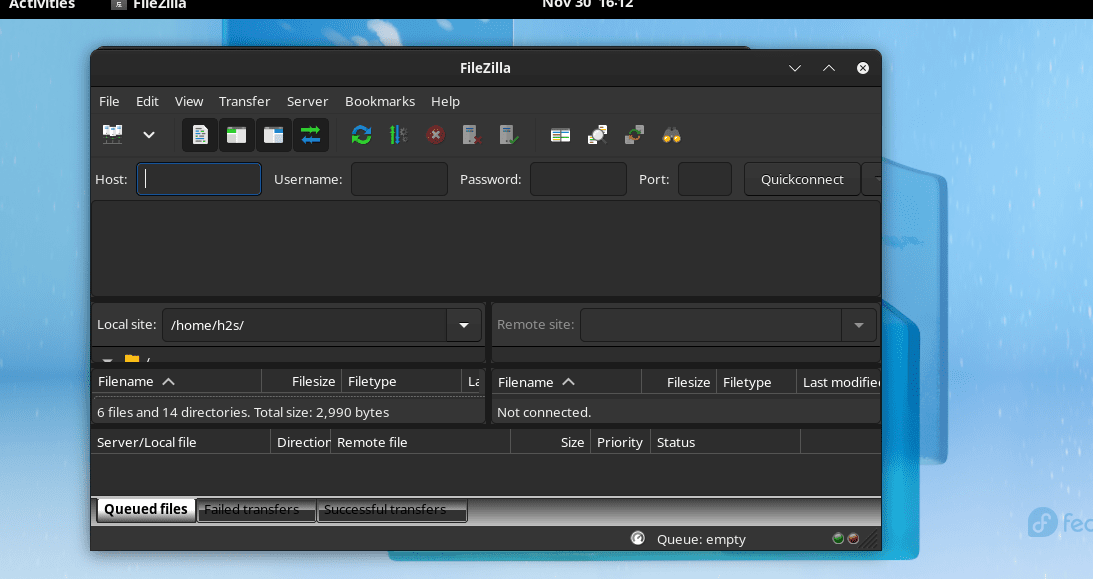
如何在 Fedora 37 上安装 FileZilla?
FileZilla 是一款流行的开源 FTP(文件传输协议)客户端,它提供了一个直观的界面来管理和传输文件。本文将详细介绍如何在 Fedora 37 上安装 FileZilla。以下是安装过程的详细步骤: 步骤一:更新系统 在安装任何软件之前…...

网终安全技术(刘化君)课后被略的答案
目录 8.HTTP客户机与Wb服务器通信通常会泄露哪些信息? 9.在TCP连接建立的3次握手阶段,攻击者为什么可以成功实施SYN Flood攻击?在实际中,如何防范此类攻击? 常用的网络漏洞扫描技术有哪几种?试举例说明。…...

架构思想之DDD
领域驱动设计(Domain-Driven Design,简称DDD)是一种架构思想,旨在通过将业务问题领域化,将业务逻辑放在核心领域中,以实现更好的软件设计和可维护性。下面将介绍如何实现DDD的Java实现,包括如何…...

FinClip | 2023 年 4 月产品大事记
我们的使命是使您(业务专家和开发人员)能够通过小程序解决您的关键业务流程挑战。不妨让我们看看在本月的产品与市场发布亮点,看看它们如何帮助您实现目标。 产品方面的相关动向👇👇👇 全新版本的小程序统…...

试论什么是圣人境界
人类进化方向就是不断的提高智力。鼓吹体力都是反人类。 圣人是人类能够达到的最高境界,再上一层就是神了。按照中华传统,说圣人就是神也是正确的。 圣人境界是什么样子的?在这一点上,孔子给予了答案:吾道一以贯之。掌…...
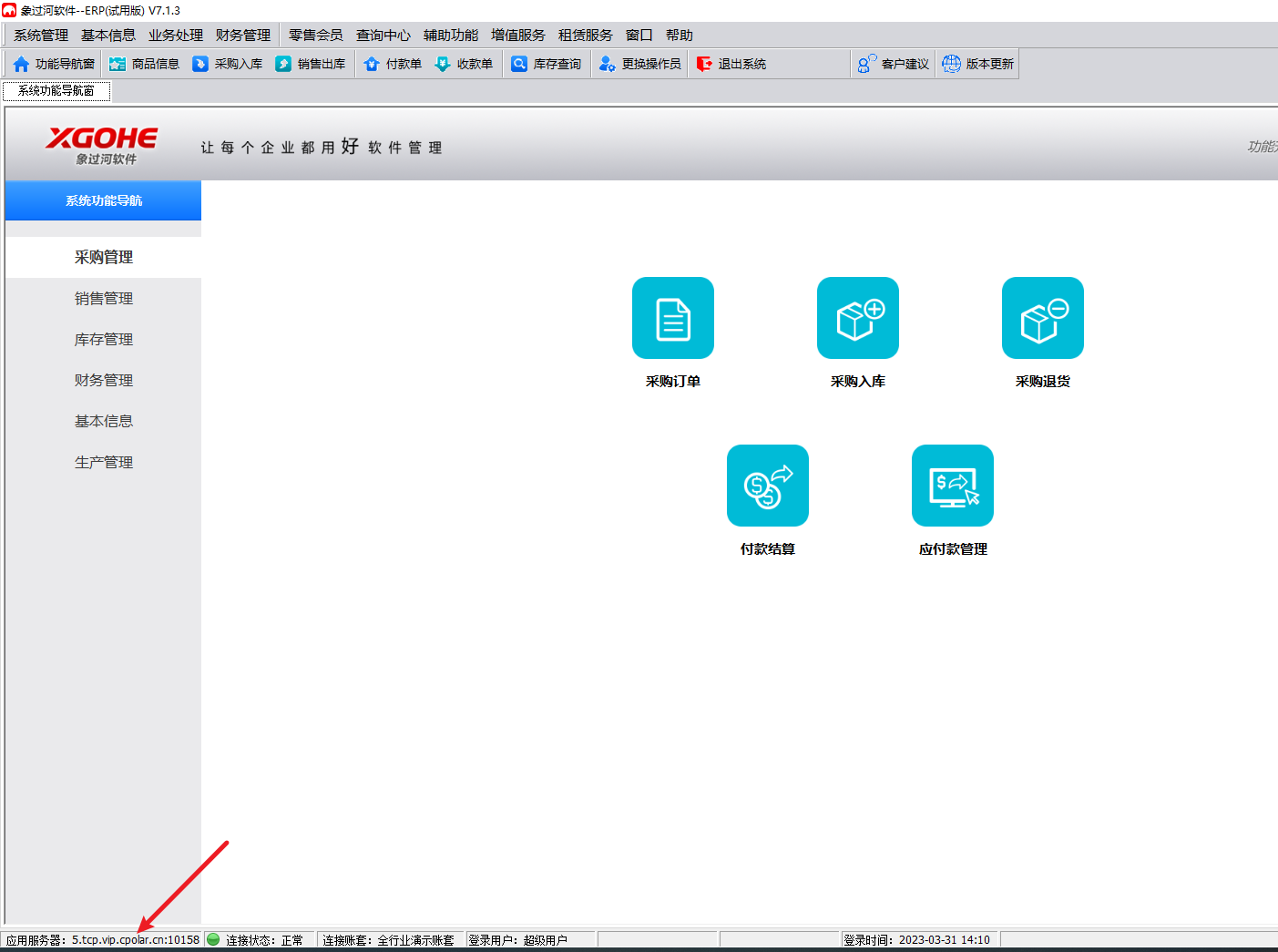
在外远程登录局域网下的象过河ERP管理系统,无需公网IP
文章目录 概述1.查看象过河服务端端口2.内网穿透3. 异地公网连接4. 固定公网地址4.1 保留一个固定TCP地址4.2 配置固定TCP地址 5. 使用固定地址连接 转发自CSDN远程穿透的文章:公网远程访问公司内网象过河ERP系统「内网穿透」 概述 ERP系统对于企业来说重要性不言而…...

golang 服务中 context 超时处理的思考
文章目录 前言起因:日志告警引发的思考什么是contextcontext的作用context超时之后继续执行 or 中断 最后 前言 公司运行的服务代码中,随处可见各种各样的日志信息,其中大多数是用来记录各种异常的日志,一方面,当出现…...

遇到Uniapp配置meta不生效怎么解决
Uniapp是一种基于 Vue.js 的跨平台应用开发框架,其开发简单、易上手,可以快速构建出 iOS、Android 和 H5 页面,成为现在移动应用开发的重要工具之一。然而,跨平台应用的开发也带来了一些问题,比如本文即是解决 uniapp …...

C语言基础知识:位与位字段
目录 位与字节 位 比特 字节 对齐特性 位字段 位与字节 位 二进制数系统中,每个0或1就是一个位(bit),位是数据存储的最小单位。其中8 bit就称为一个字节(Byte)。计算机中的CPU位数指的是CPU一次能处理的最大位数࿰…...
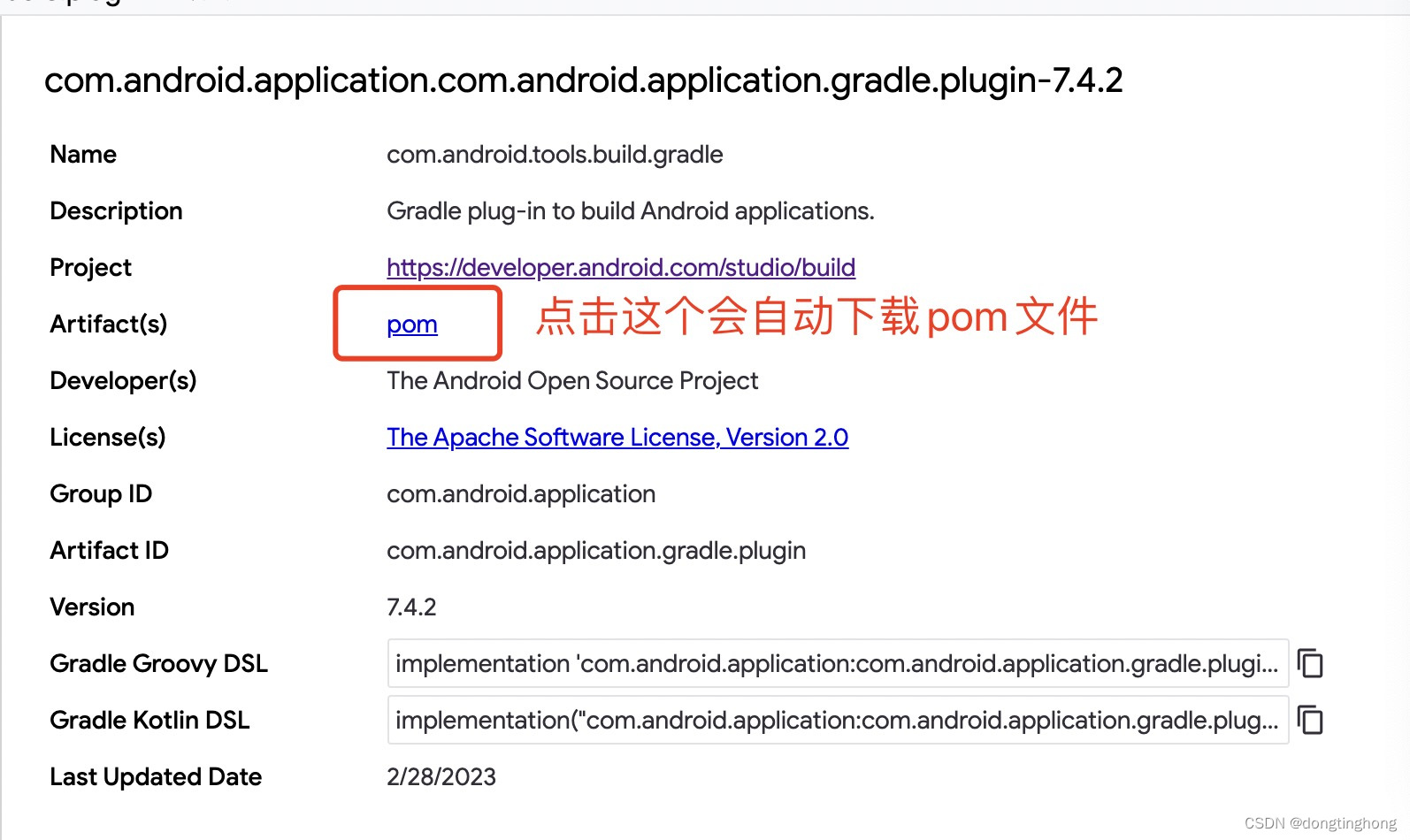
新版android studio gradle插件7.4.2.pom一直无法下载问题
android studio同步时候出现org.gradle.api.plugins.UnknownPluginException,Plugin [id: com.android.application, version: 7.4.2] was not found in any of the following sources: pom插件一直无法下载,搞了好几天,简直想砸电脑&#x…...

Shell——变量和引用
1.总结变量的类型及含义? 2.实现课堂案例计算长方形面积?(6种方式) 3.定义变量urlhttps://blog.csdn.net/weixin_45029822/article/details/103568815 (通过多种方法实现) 1)截取网站访问的协…...

实际开发中一些实用的JS数据处理方法
写在开头 JavaScript 是一种脚本语言,最初是为了网页提供交互式前端功能而设计的,而现在,通过 Node.js,JavaScript 还可以用于编写服务器端代码。 JavaScript 具有动态性、基于原型的面向对象特性、弱类型、多范式、支持闭包执行…...
10:00进去,10:05就出来了,这问的也太变态了···
从外包出来,没想到死在另一家厂子了。 自从加入这家公司,每天都在加班,钱倒是给的不少,所以也就忍了。没想到5月一纸通知,所有人不许加班,薪资直降30%,顿时有吃不起饭的赶脚。 好在有个兄弟内推…...

GPT时代,最令人担心的其实是“塔斯马尼亚效应”
目录 教育到底教什么? 过度依赖GPT可能导致文明退化 GPT可以帮助人类破解“学海无涯极限”悖论 春季学期伊始,全球各地的老师们如临大敌,因为学生们带着ChatGPT杀过来了。Study.com的调研显示,每10个学生中就有超过9个知道Chat…...

基于容器技术和服务发现的全新大数据平台弹性伸缩方法
随着科技的不断发展,各个行业都在不断地数字化和智能化。在这个过程中,大数据技术成为了许多行业的重要支撑。而随着大数据技术的普及,行业分类和设备装置的不断更新换代,弹性伸缩成为了一个不可避免的问题。本文将介绍基于服务发…...

php8 match
刚从 php7 升级到 php8 时 我在使用 switch 语句,结果出现了一个提示: "switch statement can be converted to match expression" 翻译过来就是: switch语句可以转换为match表达式 我当时在想,match 应该是php8 的…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
