CF 751 --B. Divine Array
Black is gifted with a Divine array a consisting of n (1≤n≤2000) integers. Each position in a has an initial value. After shouting a curse over the array, it becomes angry and starts an unstoppable transformation.
The transformation consists of infinite steps. Array a changes at the i-th step in the following way: for every position j, aj becomes equal to the number of occurrences of aj in a before starting this step.
Here is an example to help you understand the process better:
| Initial array: | 2 1 1 4 3 1 2 |
| After the 1-st step: | 2 3 3 1 1 3 2 |
| After the 2-nd step: | 2 3 3 2 2 3 2 |
| After the 3-rd step: | 4 3 3 4 4 3 4 |
| ... | ... |
In the initial array, we had two 2-s, three 1-s, only one 4 and only one 3, so after the first step, each element became equal to the number of its occurrences in the initial array: all twos changed to 2, all ones changed to 3, four changed to 1 and three changed to 1.
The transformation steps continue forever.
You have to process q queries: in each query, Black is curious to know the value of ax after the k-th step of transformation.
Input
Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤1000). Description of the test cases follows.
The first line of each test case contains an integer n (1≤n≤2000) — the size of the array a.
The second line of each test case contains n integers a1,a2,…,an, (1≤ai≤n) — the initial values of array a.
The third line of each test case contains a single integer q (1≤q≤100000) — the number of queries.
Next q lines contain the information about queries — one query per line. The i-th line contains two integers xi and ki (1≤xi≤n; 0≤ki≤10^9), meaning that Black is asking for the value of axi after the ki-th step of transformation. ki=0 means that Black is interested in values of the initial array.
It is guaranteed that the sum of n over all test cases doesn't exceed 2000 and the sum of q over all test cases doesn't exceed 100000.
Output
For each test case, print q answers. The i-th of them should be the value of axi after the ki-th step of transformation. It can be shown that the answer to each query is unique.
input
2
7
2 1 1 4 3 1 2
4
3 0
1 1
2 2
6 1
2
1 1
2
1 0
2 1000000000
output
1
2
3
3
1
2
题意:给定一个序列,一次转化会把a[ i ]变成a[ i ]在此时序列中出现的次数,然后给q个询问,问k次转化后,a[x]的值。
解析:因为询问个数很多,如果我们每次询问都从头开始转化,那么就会超时了,因此我们可以先把每个询问读进来,离线操作,k从小到大开始记录答案。
注意:可以发现一个序列经过若干次转化后,当每个a[ i ]等于出现次数时,那么序列就不会再发生变化。
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int a[N];
struct s
{int x,k,ans,id;
}tr[N];
bool cmp1(s a,s b)//根据k从小到大排序
{return a.k<b.k;
}
bool cmp2(s a,s b)//为了根据输入顺序输出答案
{return a.id<b.id;
}
void solve()
{int n,q;scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);scanf("%d",&q);for(int i=1;i<=q;i++) scanf("%d%d",&tr[i].x,&tr[i].k),tr[i].id=i;sort(tr+1,tr+q+1,cmp1);//根据k排序int cnt=0,f=0;//cnt和f分别表示当前第几轮转化和是否是达到不变状态for(int i=1;i<=q;i++){int x=tr[i].x,k=tr[i].k;while(k>cnt&&!f){vector<int> mp(n+5);//记录每个数出现的个数int ok=1;//判断是否每个数都等于当前出现次数for(int j=1;j<=n;j++) mp[a[j]]++;//对应出现次数+1for(int j=1;j<=n;j++){if(a[j]!=mp[a[j]]){ok=0;//没有达到不变状态break;}}if(ok) f=1;if(f) break;for(int j=1;j<=n;j++) a[j]=mp[a[j]];//更新序列cnt++;//轮数+1}tr[i].ans=a[x];//记录答案}sort(tr+1,tr+q+1,cmp2);//根据输入顺序输出答案for(int i=1;i<=q;i++) printf("%d\n",tr[i].ans);
}
int main()
{int t=1;scanf("%d",&t);while(t--) solve();return 0;
}相关文章:

CF 751 --B. Divine Array
Black is gifted with a Divine array a consisting of n (1≤n≤2000) integers. Each position in a has an initial value. After shouting a curse over the array, it becomes angry and starts an unstoppable transformation. The transformation consists of infinite…...

Springcloud1--->Eureka注册中心
目录 Eureka原理Eureka入门案例编写EurekaServer将user-service注册到Eureka消费者从Eureka获取服务 Eureka详解基础架构高可用的Eureka Server失效剔除和自我保护 Eureka原理 Eureka:就是服务注册中心(可以是一个集群),对外暴露自…...
面试阿里、字节全都一面挂,被面试官说我的水平还不如应届生
测试员可以先在大厂镀金,以后去中小厂毫无压力,基本不会被卡,事实果真如此吗?但是在我身上却是给了我很大一巴掌... 所谓大厂镀金只是不卡简历而已,如果面试答得稀烂,人家根本不会要你。况且要不是大厂出来…...

JAVA开发(记一次删除完全相同pgSQL数据库记录只保留一条)
进行数据管理时,无效数据可能会对生产力和决策质量造成严重的影响。如何发现和处理无效数据变得愈发重要。一起来唠唠你会如何处理无效数据吧~ 方向一:介绍无效数据的概念 最近遇到了pg数据库表中的大量数据重复了,需要删除其中的一条。一条…...

音视频八股文(7)-- 音频aac adts三层结构
AAC介绍 AAC(Advanced Audio Coding)是一种现代的音频编码技术,用于数字音频的传输和存储领域。AAC是MPEG-2和MPEG-4标准中的一部分,可提供更高质量的音频数据,并且相比于MP3等旧有音频格式,AAC需要更少的…...
Docker代码环境打包进阶 - DockerHub分享镜像
1. Docker Hub介绍 Docker Hub是一个广泛使用的容器镜像注册中心,为开发人员提供了方便的平台来存储、共享和分发Docker容器镜像。它支持版本控制、访问控制和自动化构建,并提供了丰富的公共镜像库,方便开发人员快速获取和使用各种开源应用和…...

SQL进阶-having子句的力量
SQL进阶-having子句的力量 having子句是理解SQL面向集合这一本质的关键。 在以前的SQL标准里面,having子句必须和group by子句一起使用,但是按照现在的SQL标准,having子句是可以单独使用的 可以与case 表达式或者自连接等结合使用。表不是文件…...
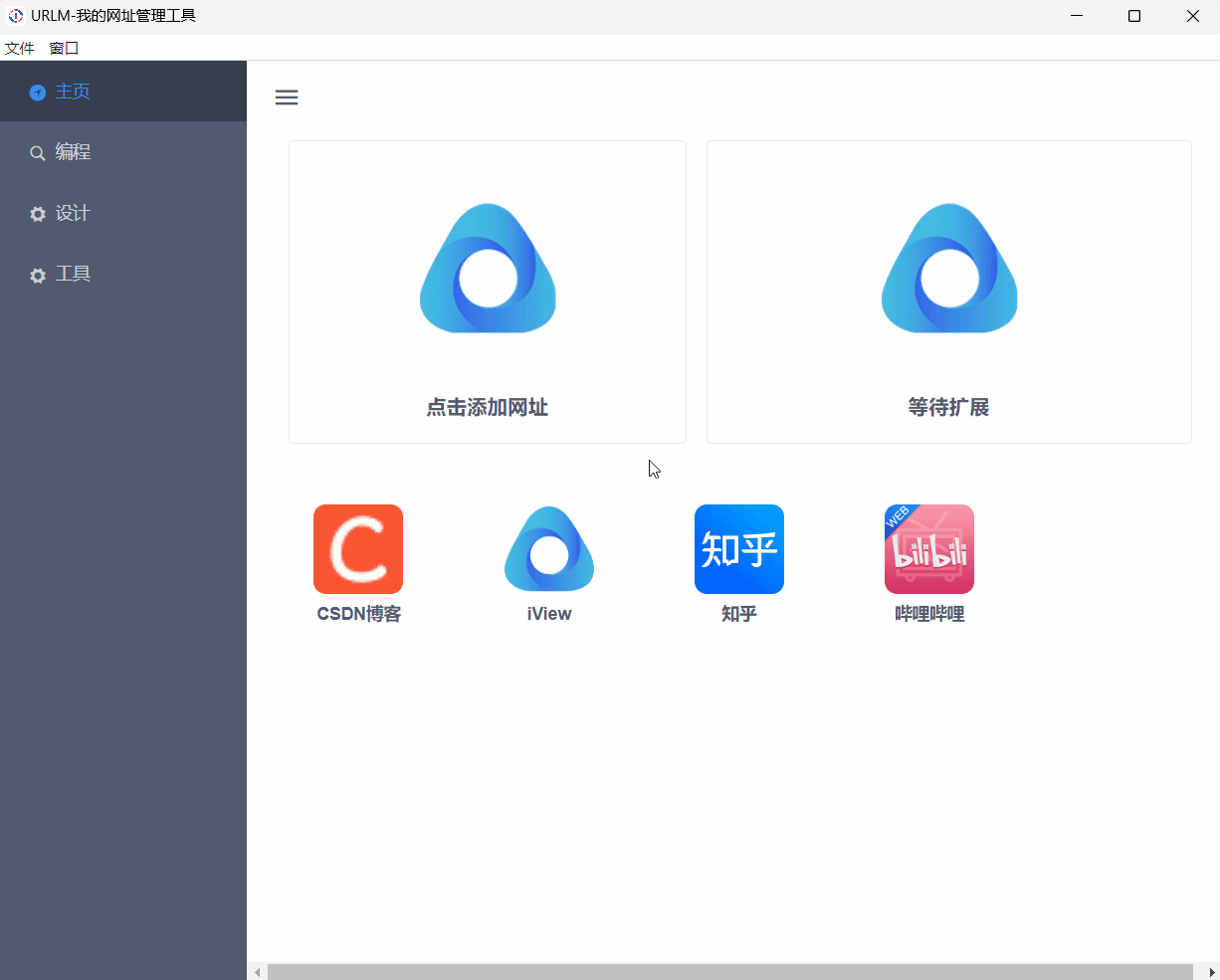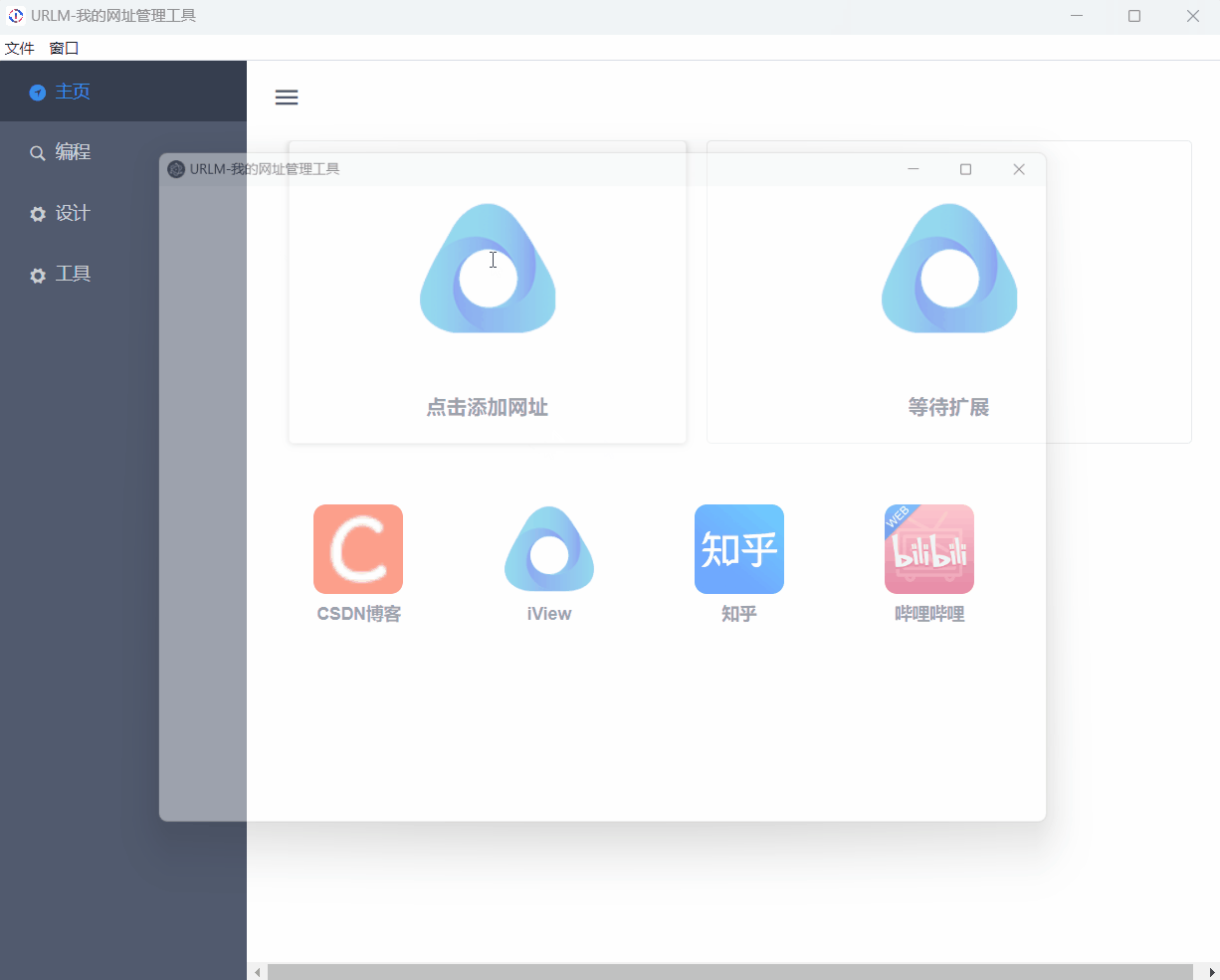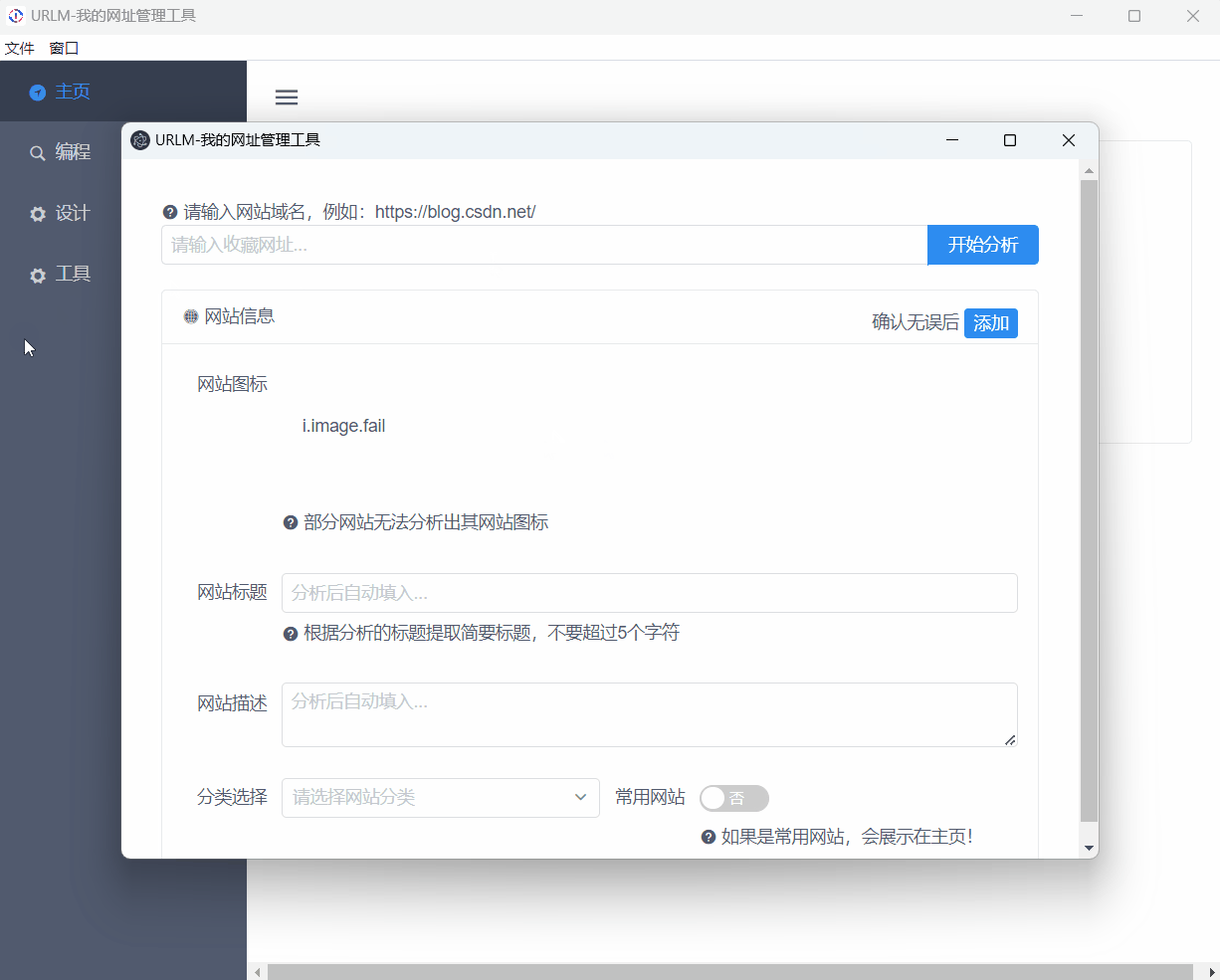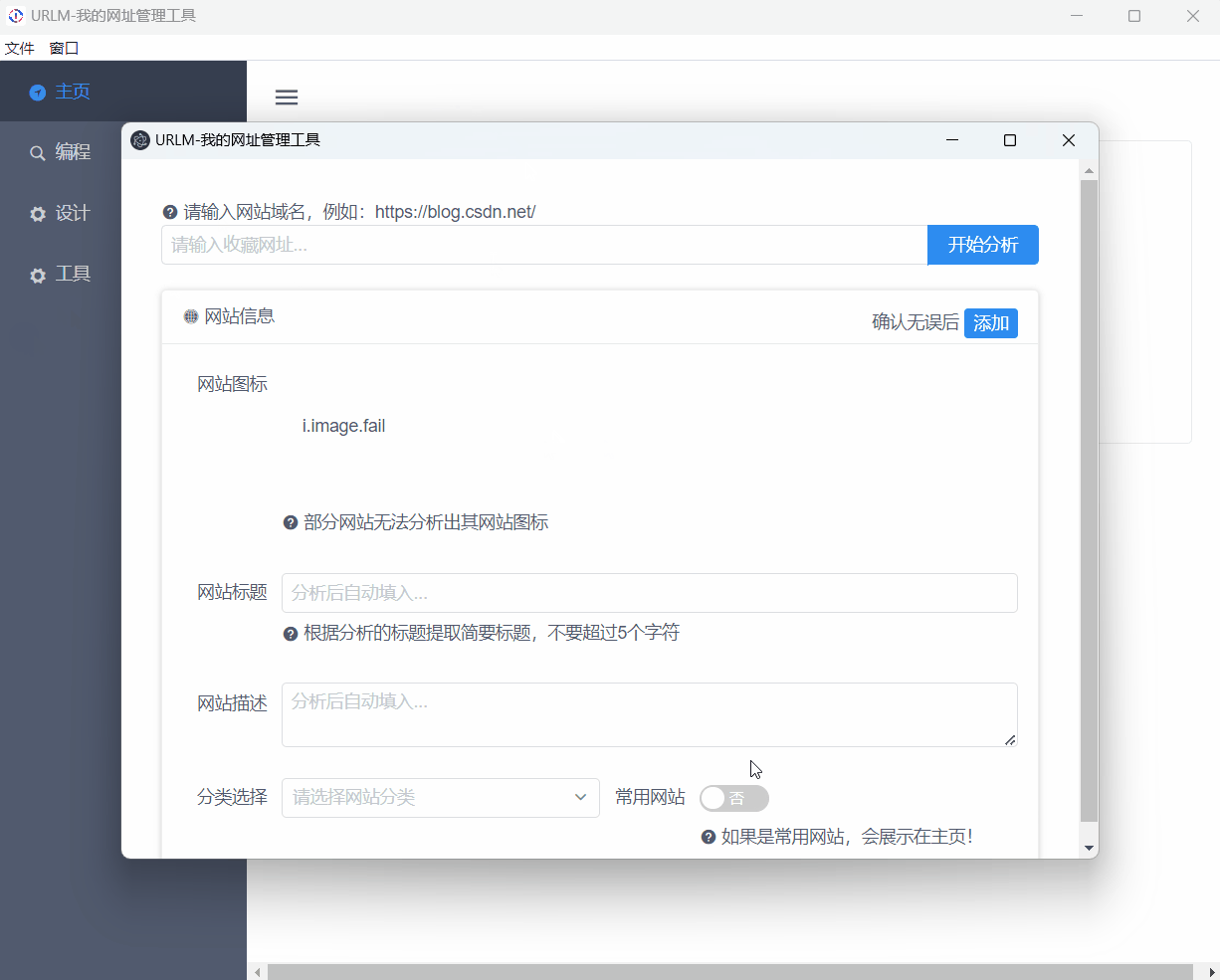
Electron 如何创建模态窗口?
目录 前言一、模态窗口1.Web页面模态框2.Electron中的模态窗口3.区分父子窗口与模态窗口 二、实际案例使用总结 前言 模态框是一种常用的交互元素,无论是在 Web 网站、桌面应用还是移动 APP 中,都有其应用场景。模态框指的是一种弹出窗口,它…...

诺贝尔化学奖:酶分子“定向进化”
2018年,诺贝尔化学奖迎来了历史上第五位女性得主——加州理工学院的Frances H. Arnold教授,以表彰她在“酶的定向进化”这一领域的贡献。 1、“酶的定向进化”到底是什么? 这里有三个点,“酶”、“进化”还有“定向”:…...

Centos8下源码编译安装运行Primihub
参考文献 PrimiHub 本地编译启动How to install Bazel on CentOS 8 Linux or Redhat 8/7 编译启动步骤 由于历史原因,服务器是Centos8操作系统,所以源码编译异常的麻烦。特此记录如下。 采用源码编译方式可以在一步步的运行过程中对整个流程进行深刻…...

嘉兴桐乡考证培训-23年教资认定注意事项你知道吗?
又到了新的一年了,去年错过认定的同学们可以竖起耳朵啦~ 每年认定机会有两次,大部分省份一般上半年下半年各一次。 问:在校生可以认定么? 答:可以,但有年级限制:本科生大四最后一学期…...
oracle客户端的安装教程
文章目录 一、安装前的准备工作 1.1、百度网盘安装包的连接 1.2、百度网盘oracle11g软件包 二、oracle数据库客户端的安装与数据的准备 安装步骤 前言 本文主要讲解oracle客户端的安装与简单使用过程 一、安装前的准备工作 1.1、百度网盘安装包的连接 客户端的软件包 …...
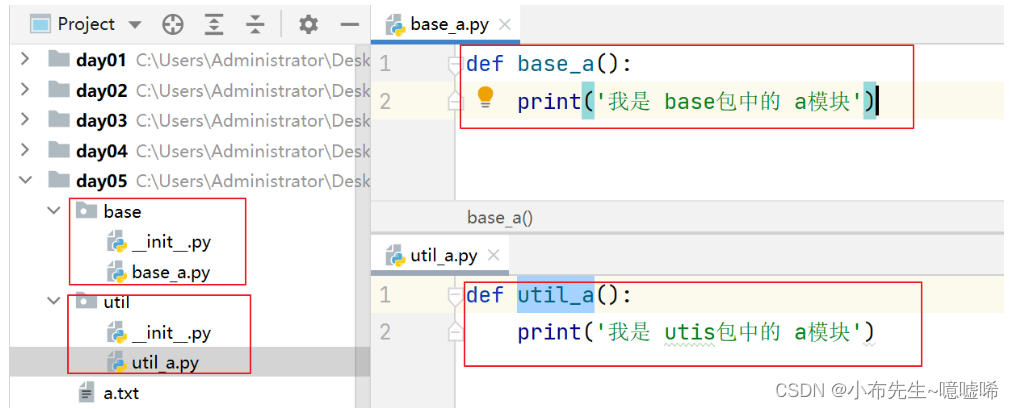
python 文件操作 , 异常处理 , 模块和包
文件操作 1.写数据 # open(name, mode) # name:是要打开的目标文件名的字符串(可以包含文件所在的具体路径)。 # mode:设置打开文件的模式(访问模式):只读、写入、追加等。 #1.打开文件---通道建立--申请资源 # w 模式会清空之前的内…...
)
AIGC技术研究与应用 ---- 下一代人工智能:新范式!新生产力!(1-简介)
文章大纲 AI GC简介决策式/分析式AI(Discriminant/Analytical AI)和生成式AI (Generative AI)参考文献与学习路径模型进化券商研报陆奇演讲AI GC 《我,机器人》中所演绎的一样,主角曾与机器人展开了激烈的辩论,面对“机器人能写出交响乐吗?”“机器人能把画布变成美丽…...
Flask restful分页接口实现
1.先定义一个工作信息表: 指定一些相关的字段:工作名称、年限、级别等 class Work(db.Model):__tablename__ = workid = db.Column(db.Integer, primary_key=True)workName = db.Column(db.String(5),nullable=False)year = db.Column(db.String(20), nullable=False)level = …...

27事务管理AOP
一、MySQL事务回顾 二、Spring事务管理 Spring框架的第一大核心:IOC控制反转 在DeptServiceImpl下删除部门方法下新加一个删除员工信息的操作,注意:此时的id是部门id。 1、问题分析 2、Transactional-Spring事务管理 一般是在Service实现类的…...

煤矿电子封条实施方案 yolov7
煤矿电子封条实施方案采用YOLOv7网络模型算法技术,煤矿电子封条实施算法模型过将全国各省矿山实时监测数据,实现对全国各矿山及时有效的处理及分析。YOLOv7 的发展方向与当前主流的实时目标检测器不同,研究团队希望它能够同时支持移动 GPU 和…...

Linux-inode和block概述
操作系统的文件数据除了实际内容之外,通常含有非常多的属性,例如Linux操作系统的文件权限与文件属性。文件系统通常会将这两部分内容分别存放在inode和block中。 inode 和 block 概述 文件是存储在硬盘上的,硬盘的最小存储单位叫做扇区sect…...

安卓开发投屏反控实现方式
在安卓开发中,可以通过MediaProjection API来实现屏幕投屏的功能,同时也可以通过Socket通信实现反控功能。下面将详细介绍实现步骤和注意事项。 1. 创建MediaProjectionManager对象 首先,我们需要创建一个MediaProjectionManager对象&#…...
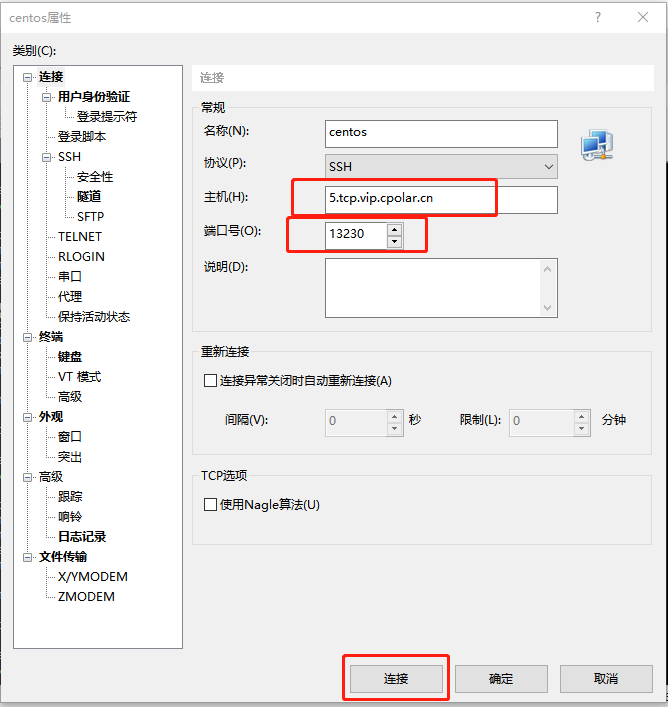
外网SSH远程连接linux服务器「cpolar内网穿透」
✨个人主页:bit me👇 目 录 视频教程🌴1. Linux CentOS安装cpolar☘️2. 创建TCP隧道🎍3. 随机地址公网远程连接🎋4. 固定TCP地址🎄5. 使用固定公网TCP地址SSH远程 转载自内网穿透工具的文章:无…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...

机器学习复习3--模型评估
误差与过拟合 我们将学习器对样本的实际预测结果与样本的真实值之间的差异称为:误差(error)。 误差定义: ①在训练集上的误差称为训练误差(training error)或经验误差(empirical error&#x…...
