动态规划-树形DP
树的重心
题目
链接:https://www.acwing.com/problem/content/848/
给定一颗树,树中包含 n n n 个结点(编号 1 ∼ n 1 \sim n 1∼n)和 n − 1 n-1 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n n n,表示树的结点数。
接下来 n − 1 n-1 n−1 行,每行包含两个整数 a a a 和 b b b,表示点 a a a 和点 b b b 之间存在一条边。
输出格式
输出一个整数 m m m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1 ≤ n ≤ 1 0 5 1 \le n \le 10^5 1≤n≤105
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例:
4
思路
任取一点u,如果以u为重心,则分为如下两类:
- u的子树
- u上面的部分
需要算出这两者的节点数,取最大值。具体细节见代码
代码
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 1e5 + 10;
vector<int> e[N];
int n;
int sz[N]; //记录u的最大子树的节点数
int ans = 1e9;void dfs(int u, int fa) { //u:当前点,fa:父节点sz[u] = 1;int mx = 0; //记录u上面的点和子节点连通块的最大值for (auto j: e[u]) {if (j == fa) continue; //防止向上搜索dfs(j, u);sz[u] += sz[j];mx = max(mx, sz[j]);}mx = max(mx, n - sz[u]);ans = min(ans, mx);
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;for (int i = 1; i <= n - 1; i++) {int x, y;cin >> x >> y;e[x].push_back(y);e[y].push_back(x);}dfs(1, 0);cout << ans << endl;return 0;
}
树的最长直径
题目
链接:https://www.acwing.com/problem/content/1074/
给定一棵树,树中包含 $ n $ 个结点(编号$ 1 ~ n $)和 $ n-1 $ 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 $ n $。
接下来 $ n-1 $ 行,每行包含三个整数 $ a_i,b_i,c_i $,表示点 $ a_i $ 和 $ b_i $ 之间存在一条权值为 $ c_i $ 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
$ 1 \le n \le 10000 $,
$ 1 \le a_i,b_i \le n $,
$ -10^5 \le c_i \le 10^5 $
输入样例:
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22
思路
任取一点u,从u点向下搜索,返回时收集边的权值,记录两条路径:
- d1:记录从u点往下走的最长路径的长度
- d2:记录从u点往下走的次长路径的长度
更新答案:ans=max(ans,d1+d2)
代码
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 10010;
int n, ans;
typedef struct edge {int v, w;
} edge;vector<edge> e[N];int dfs(int u, int fa) {int d1 = 0, d2 = 0;//最长和次长for (auto j: e[u]) {auto [v, w] = j;if (v == fa) continue;int d = dfs(v, u) + w;if (d >= d1) d2 = d1, d1 = d;else if (d > d2) d2 = d;}ans= max(ans,d1+d2);return d1;
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;for (int i = 1; i < n; i++) {int a, b, c;cin >> a >> b >> c;e[a].push_back({b, c});e[b].push_back({a, c});}dfs(1, 0);cout << ans << endl;return 0;
}
树的中心
题目
链接:https://www.acwing.com/problem/content/1075/
给定一棵树,树中包含 $ n $ 个结点(编号$ 1 ~ n $)和 $ n-1 $ 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 $ n $。
接下来 $ n-1 $ 行,每行包含三个整数 $ a_i,b_i,c_i $,表示点 $ a_i $ 和 $ b_i $ 之间存在一条权值为 $ c_i $ 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
$ 1 \le n \le 10000 $,
$ 1 \le a_i,b_i \le n $,
$ 1 \le c_i \le 10^5 $
输入样例:
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例:
2
思路
开一个数组p:p[u]记录从u点向下走点最长路径是从哪个点下去的
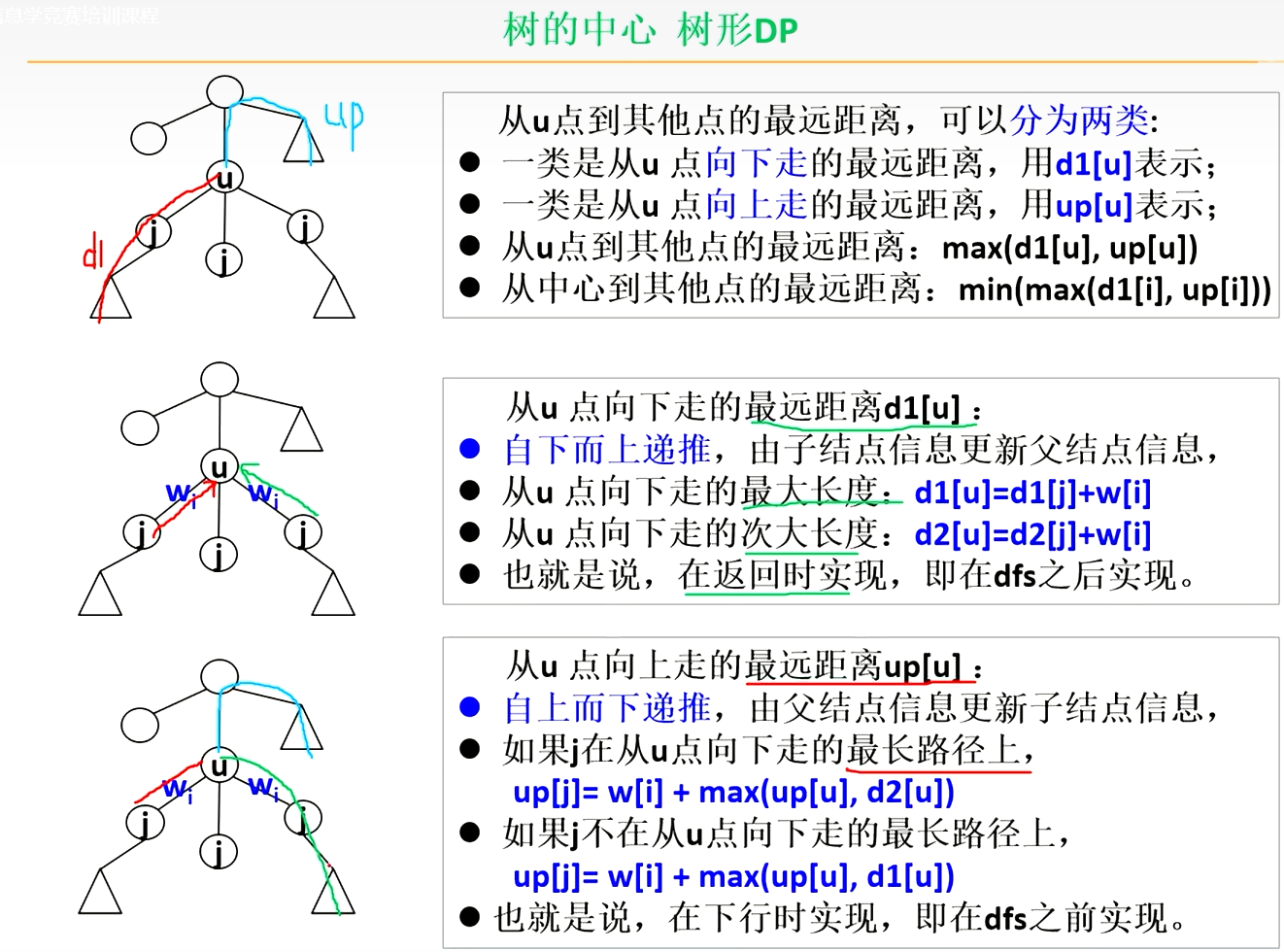
代码
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 100010;
int ans = 2e9;
int n;
typedef struct edge {int v, w;
} edge;vector<edge> e[N];
int d1[N], d2[N], up[N], p[N];void dfs1(int x, int fa) {for (auto item: e[x]) {int y = item.v, w = item.w;if (y == fa) continue;dfs1(y, x);if (d1[y] + w > d1[x]) {d2[x] = d1[x], d1[x] = d1[y] + w, p[x] = y;} else if (d1[y] + w > d2[x]) d2[x] = d1[y] + w;}
}void dfs2(int x, int fa) {for (auto item: e[x]) {int y = item.v, w = item.w;if (y == fa)continue;else if (y == p[x]) up[y] = max(up[x], d2[x]) + w;else up[y] = max(up[x], d1[x]) + w;dfs2(y, x);}
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;for (int i = 1; i <= n - 1; i++) {int a, b, c;cin >> a >> b >> c;e[a].push_back({b, c});e[b].push_back({a, c});}dfs1(1, 0);dfs2(1, 0);for (int i = 1; i <= n; i++) {ans = min(ans, max(d1[i], up[i]));}cout<<ans<<endl;return 0;
}
数字转换
题目
链接:https://www.acwing.com/problem/content/1077/
如果一个数 $ x $ 的约数之和 $ y $(不包括他本身)比他本身小,那么 $ x $ 可以变成 $ y , , , y $ 也可以变成 $ x $。
例如,$ 4 $ 可以变为 $ 3 , , , 1 $ 可以变为 $ 7 $。
限定所有数字变换在不超过 $ n $ 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
输入格式
输入一个正整数 $ n $。
输出格式
输出不断进行数字变换且不出现重复数字的最多变换步数。
数据范围
$ 1 \le n \le 50000 $
输入样例:
7
输出样例:
3
样例解释
一种方案为:$ 4 \to 3 \to 1 \to 7 $。
思路
因为每个数x的约数之和y是固定的,但是一个约数之和y有可能是很多数x产生的,因此我们可以从y向x连边,这样就可以构成一棵树了,反之就不会构成树
这样建图的方式会构造出很多的树
如何求每个数的约数:
可以使用试除法求约数,这样的时间复杂度为 O ( n n ) O(n\sqrt{n}) O(nn)本题应该可以过
也可以利用晒法的思想,对于一个数x,去枚举它的倍数(2倍,3倍…),把这些倍数的数都加上数x,这样做的时间复杂度为调和级数 l n n + C lnn+C lnn+C,因此时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
构造完树之后,求最多的变换次数即变成了求树的最长直径,可以参考代码模版。
代码
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 5e4 + 10;vector<int> e[N];
int res = 0;
int d1[N], d2[N];
bool st[N];
int n;
int sum[N];void dfs(int x, int fa) {for (auto y: e[x]) {if (y == fa) continue;dfs(y, x);if (d1[y] + 1 > d1[x]) d2[x] = d1[x], d1[x] = d1[y] + 1;else if (d1[y] + 1 > d2[x]) d2[x] = d1[y] + 1;}res = max(res, d1[x] + d2[x]);
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;//统计每个数的约数之和for (int i = 1; i <= n; i++) {for (int j = 2; j <= n / i; j++) {sum[i * j] += i;}}//建图for (int i = 2; i <= n; i++) {if (sum[i] < i) {e[sum[i]].push_back(i);st[i] = true;}}for (int i = 1; i <= n; i++)if (!st[i]) dfs(i, i);cout << res << endl;return 0;
}
相关文章:

动态规划-树形DP
树的重心 题目 链接:https://www.acwing.com/problem/content/848/ 给定一颗树,树中包含 n n n 个结点(编号 1 ∼ n 1 \sim n 1∼n)和 n − 1 n-1 n−1 条无向边。 请你找到树的重心,并输出将重心删除后&#x…...
多线程基础(二)CAS无锁优化/自旋锁/乐观锁、ABA问题
CAS (Compare And Set)比较并替换 上篇文章的锁问题解决,可以使用更高效的方法,使用AtomXXX类,AtomXXX类本身方法都是原子性的,但不能保证多个方法连续调用是原于性的。 import java.util.ArrayList; imp…...

记ABAC的落地实践
为什么使用ABAC 一般提到授权,我们就会想到角色(role)。什么样的用户拥有什么样的角色可以怎么操作什么样的资源,这是我们普遍使用的权限系统的模型。这里的角色实质上是包含了一组用户操作资源的规则集合。一旦角色被创建&#…...

【C++】C++11线程库 和 C++IO流
春风若有怜花意,可否许我再少年。 文章目录 一、C11线程库1.thread类介绍2.mutex互斥锁 和 CAS原子操作(compare and set)3.lock_guard和unique_lock4.两个线程交替打印,一个打印奇数,一个打印偶数(线程同步…...

cpp11实现线程池(六)——线程池任务返回值类型Result实现
介绍 提交任务函数submitTask中返回的Result类型应该是用Result类包装当前的task,因为出函数之后task即如下形式:return Result(task); Result和Task都要互相持有对方的指针,Task要将任务执行结果通过Result::setVal(run()) 调用传给其对应…...
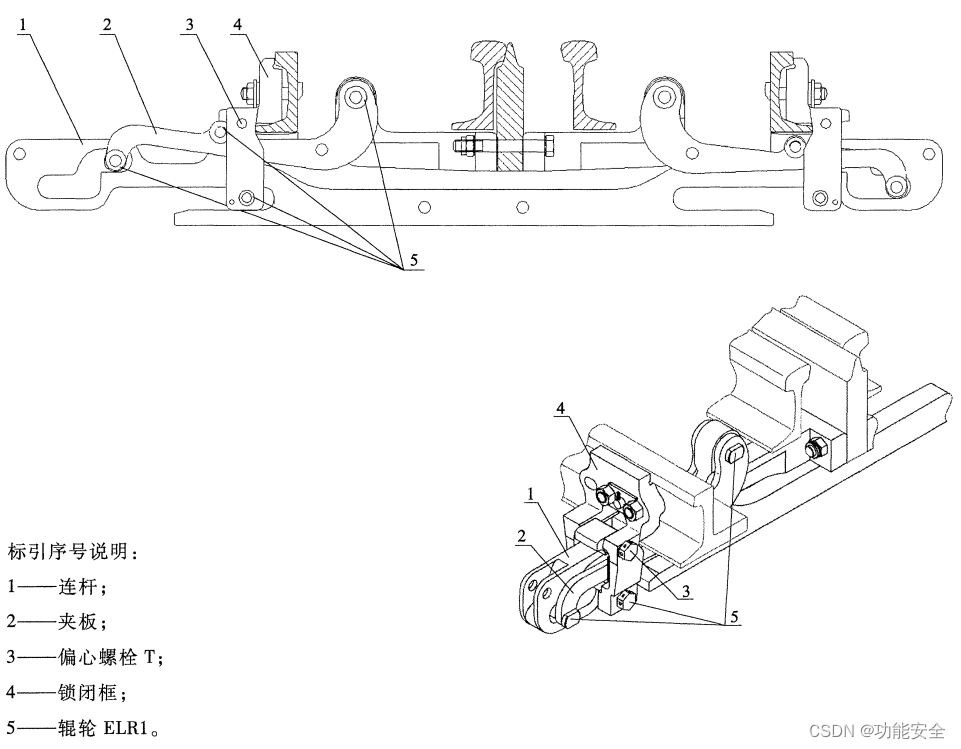
道岔外锁闭装置介绍
简述 道岔外锁闭装置是一种能可靠地锁闭尖轨和基本轨的器械。它能有效地克服尖轨在密贴时的转换阻力,即使连接杆折断,外锁闭装置仍在起着锁闭作用。外锁闭能够隔离列车通过时对转换设备的振动和冲击,提高转换设备寿命和可靠性。 产品分类 …...
idea把项目上传到码云
1. 为项目创建仓库 2. 选中中项目右击git, 先add, 在commit Directory 3. 设置远程码云项目地址 4. push项目, ok。 注意: 如果你在最后push出现以下提示,则说明提交失败 Push to origin/master was rejected(译文:推送到原点/master被拒绝…...

设计模式之责任链模式
责任链模式的定义是:使多个对象都有机会处理请求,从而避免了请求的发送者和接受者之间的耦合关系。将这些对象连成一条链,并沿着这条链传递该请求,直到有对象处理它为止。 责任链模式适合于请求需要经过多个处理器,并…...

Python--我一般都用这个模块压缩文件
打包成压缩文件很多时候都能用上,也包括了自动化中的部分应用。例如,将测试报告打包发送。 本章就来介绍其中一个模块,可以用于结合上一章的内容结合使用。 from zipfile import ZipFile ❝ ZipFile是zipfile的一个方法。 ❞ 提取zip文件 fro…...
Chapter8 :Physical Constraints(ug903)
8.1About Physical Constraints(关于物理约束) XilinxVivado集成设计环境(IDE)允许通过设置对象属性值对设计对象进行物理约束。示例包括: •I/O约束,如位置和I/O标准 •布局约束&…...
星标3.5k,一款国产的轻量级开源在线项目任务管理工具
今天给大家推荐一个轻量级的开源在线项目任务管理工具:DooTask 图片 DooTask 提供各类文档协作工具、在线思维导图、在线流程图、项目管理、任务分发、即时IM,文件管理等工具。 高效便捷的团队沟通工具 针对项目和任务建立群组,工作问题可…...

【华为OD机试真题2023B卷 JAVA】字符串摘要
华为OD2023(B卷)机试题库全覆盖,刷题指南点这里 字符串摘要 知识点字符串排序 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 给定一个字符串的摘要算法,请输出给定字符串的摘要值。 1、去除字符串中非字母的符号。 2、如果出现连续字符(不区分大小写),则输…...
Java线程概述 (一)线程介绍
文章目录 🐒个人主页🏅JavaSE系列专栏📖前言:🪅什么是程序 、进程、线程?🪅线程的生命周期🪅多线程🪅守护者线程🪅线程并行与并发🪅死锁…...

操作系统第三章——存储系统(下)
锦衣雪华玉颜色,回眸一笑天下倾 文章目录 3.2.1 虚拟内存的基本概念知识总览传统存储方式的特征,缺点局部性原理虚拟内存的定义如何实现虚拟内存技术知识总结 3.2.2 请求分页管理方式知识总览页表机制缺页中断机制地址变换机制知识回顾 3.2.3 页面置换算…...
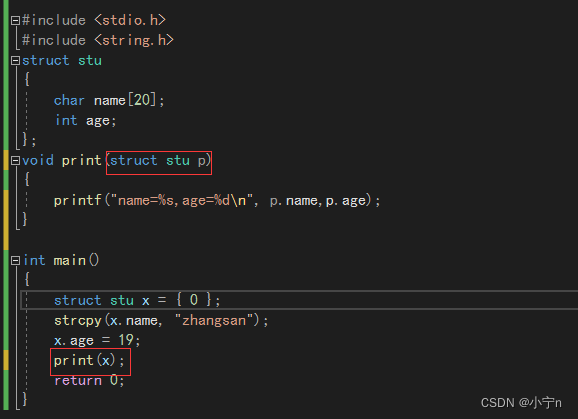
初识结构体
目录 结构体的声明 结构体的基础知识 结构体的声明 结构体成员的类型 结构体变量的定义和初始化 定义 初始化 结构体成员的访问 结构体变量访问成员 结构体指针访问指向变量的成员 结构体传参 传地址 传结构体 结论 结构体的声明 结构体的基础知识 数组ÿ…...

协程并发下数据汇总:除了互斥锁,还有其他方式吗?
1. 简介 本文介绍了在并发编程中数据汇总的问题,并探讨了在并发环境下使用互斥锁和通道两种方式来保证数据安全性的方法。 首先,通过一个实例,描述了一个并发拉取数据并汇总的案例,并使用互斥锁来确保线程安全。然后,…...

5、Ray-Actor模型和并发编程
5、Ray-Actor模型和并发编程 导航 1.简介和背景 2.Ray的基本概念和核心组件 3.分布式任务调度和依赖管理 4.对象存储和数据共享 5.Actor模型和并发编程 6.Ray的高级功能和扩展性 7.使用Ray构建分布式应用程序的案例研究 8.Ray社区和资源 9.核心框架介绍...
HNU-电路与电子学-小班2
第二次讨论 讨论题目: 1、电子秤的电桥电路可以分别用 1 个压控电阻、 2 个压控电阻、 3 个压控电阻、 4 个压控电阻实现吗?试写出每种实现的 U AB 输出表达式,并分析哪种实现电桥 电压的灵敏度(SV/ △ R )高。 …...

二分图匹配算法
匈牙利算法、Hopcroft-Karp算法和Kuhn-Munkres算法是三种常见的二分图匹配算法,它们在实现方式、时间复杂度和适用场景上有所差异。以下是它们的区别和优缺点: 匈牙利算法: 实现方式:匈牙利算法使用深度优先搜索(DFS)来寻找增广路…...
虹科技术 | 虹科EtherCAT增量编码器输入模块数据采集实操测试
1. 背景介绍 编码器是将信号或数据进行编制、转换为可用以通讯、传输和存储的信号形式的设备。编码器把角位移或直线位移转换成电信号,前者称为码盘,后者称为码尺。按照读出方式编码器可以分为接触式和非接触式两种;按照工作原理编码器可分为…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
