CF1667E Centroid Probabilities
题目描述
对于所有点数为 nnn 的树,如果其满足 对于所有 i∈[2,n]i\in [2,n]i∈[2,n],与 iii 相连的 jjj 中有且只有一个点 jjj 满足 j<ij<ij<i ,那么我们称其为好树
对于 1∼n1\sim n1∼n 每个点求出来有多少好树满足重心为 iii
这里重心定义为删去这个点后形成的所有连通块大小均小于 n−12\frac{n-1}22n−1
数据范围 3≤n≤2×1053\le n\le 2\times 10^53≤n≤2×105 且 nnn 为奇数(所以不存在树有多个重心的情况)
题解
设m=n+12m=\frac{n+1}{2}m=2n+1,fif_ifi表示iii的子树大小≥m\ge m≥m的方案数
枚举iii的子树大小jjj,则有式子
fi=(i−1)∑j=mn−i+1(n−ij−1)(j−1)!(n−j−1)!f_i=(i-1)\sum_{j=m}^{n-i+1}\binom{n-i}{j-1}(j-1)!(n-j-1)!fi=(i−1)j=m∑n−i+1(j−1n−i)(j−1)!(n−j−1)!
前面的i−1i-1i−1是钦定iii的父亲,组合数是从iii后面的点中选出属于iii子树的点,两个阶乘是为了计算两个点集连成树的方案数
=(i−1)∑j=mn−i+1(n−i)!(j−1)!(n−i−j+1)!(j−1)!(n−j−1)!=(i-1)\sum_{j=m}^{n-i+1}\frac{(n-i)!}{(j-1)!(n-i-j+1)!}(j-1)!(n-j-1)!=(i−1)j=m∑n−i+1(j−1)!(n−i−j+1)!(n−i)!(j−1)!(n−j−1)!
=(i−1)(n−i)!∑j=mn−i+1(n−j−1)!(n−i−j+1)!=(i-1)(n-i)!\sum_{j=m}^{n-i+1}\frac{(n-j-1)!}{(n-i-j+1)!}=(i−1)(n−i)!j=m∑n−i+1(n−i−j+1)!(n−j−1)!
=(n−i)!(i−1)!∑j=mn−i+1(n−j−1)!(n−i−j+1)!(i−2)!=(n-i)!(i-1)!\sum_{j=m}^{n-i+1}\frac{(n-j-1)!}{(n-i-j+1)!(i-2)!}=(n−i)!(i−1)!j=m∑n−i+1(n−i−j+1)!(i−2)!(n−j−1)!
=(n−i)!(i−1)!∑j=mn−i+1(n−j−1i−2)=(n-i)!(i-1)!\sum_{j=m}^{n-i+1}\binom{n-j-1}{i-2}=(n−i)!(i−1)!j=m∑n−i+1(i−2n−j−1)
=(n−i)!(i−1)!∑k=i−2n−m−1(ki−2)=(n-i)!(i-1)!\sum_{k=i-2}^{n-m-1}\binom{k}{i-2}=(n−i)!(i−1)!k=i−2∑n−m−1(i−2k)
=(n−i)!(i−1)!(n−mi−1)=(n-i)!(i-1)!\binom{n-m}{i-1}=(n−i)!(i−1)!(i−1n−m)
于是fif_ifi可以O(n)O(n)O(n)计算,考虑容斥求出ansians_iansi表示以iii为重心的方案数,枚举它的儿子jjj子树大小≥m\ge m≥m,显然对于jjj来说父亲为哪个方案数都是一样的,所以以iii为父亲的方案数就是fjj−1\frac{f_j}{j-1}j−1fj,即答案为ansi=fi−∑j=i+1fjj−1ans_i=f_i-\sum_{j=i+1}\frac{f_j}{j-1}ansi=fi−∑j=i+1j−1fj
code\text{code}code
#include<cstdio>
#define ll long long
using namespace std;
const ll mod=998244353;
ll ksm(ll a,ll b)
{if(b==0) return 1;ll tmp=ksm(a,b>>1);if(b&1) return tmp*tmp%mod*a%mod;else return tmp*tmp%mod;
}
const int N=2e5+1000;
int n;
ll f[N+10],fac[N+10],inv[N+10];
ll C(int n,int m){if(m>n) return 0;return fac[n]*inv[m]%mod*inv[n-m]%mod;}
int main()
{scanf("%d",&n);fac[0]=inv[0]=1;for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod,inv[i]=ksm(fac[i],mod-2);f[1]=fac[n-1];int m=n+1>>1;for(int i=2;i<=n;i++) f[i]=fac[i-1]*fac[n-i]%mod*C(n-m,i-1)%mod;ll res=0;for(int i=n;i>=1;i--){ll tmp=f[i];f[i]=(f[i]+mod-res)%mod;res+=tmp*ksm(i-1,mod-2)%mod,res%=mod;}for(int i=1;i<=n;i++) printf("%lld ",f[i]);puts("");return 0;
}
相关文章:

CF1667E Centroid Probabilities
题目描述 对于所有点数为 nnn 的树,如果其满足 对于所有 i∈[2,n]i\in [2,n]i∈[2,n],与 iii 相连的 jjj 中有且只有一个点 jjj 满足 j<ij<ij<i ,那么我们称其为好树 对于 1∼n1\sim n1∼n 每个点求出来有多少好树满足重心为 iii …...
全网详细总结com.alibaba.fastjson.JSONException: syntax error, position at xxx常见错误方式
文章目录1. 复现问题2. 分析问题3. 解决问题4. 该错误的其他解决方法5. 重要补充1. 复现问题 今天在JSONObject.parse(json)这个方法时,却报出如下错误: com.alibaba.fastjson.JSONException: syntax error, position at 0, name usernameat com.aliba…...
快速部署个人导航页:美好的一天从井然有序开始
很多人都习惯使用浏览器自带的收藏夹来管理自己的书签,然而收藏夹存在着一些问题。 经过长时间的累积,一些高频使用的重要网站和偶尔信手收藏的链接混在了一起,收藏夹因为内容过多而显得杂乱无章;收藏夹没有什么美观可言…...

【Python】如何在 Python 中使用“柯里化”编写干净且可重用的代码
对于中级Python开发者来说,了解了Python的基础语法、库、方法,能够实现一些功能之后,进一步追求的就应该是写出优雅的代码了。 这里介绍一个很有趣的概念“柯里化”。 所谓柯里化(Currying)是把接受多个参数的函数变换…...
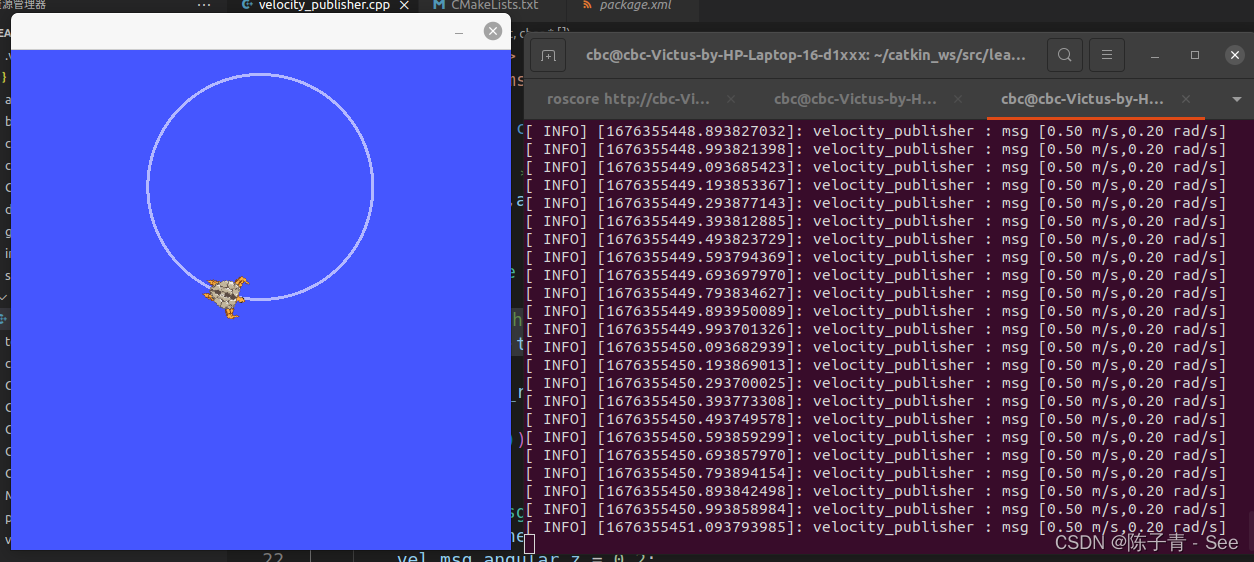
ROS笔记(4)——发布者Publisher与订阅者Subscribe的编程实现
发布者 以小海龟的话题消息为例,编程实现发布者通过/turtle1/cmd_vel 话题向 turtlesim节点发送消息,流程如图 步骤一 创建功能包(工作空间为~/catkin_ws/src) $ cd ~/catkin_ws/src $ catkin_create_pkg learning_topic roscpp rospy s…...
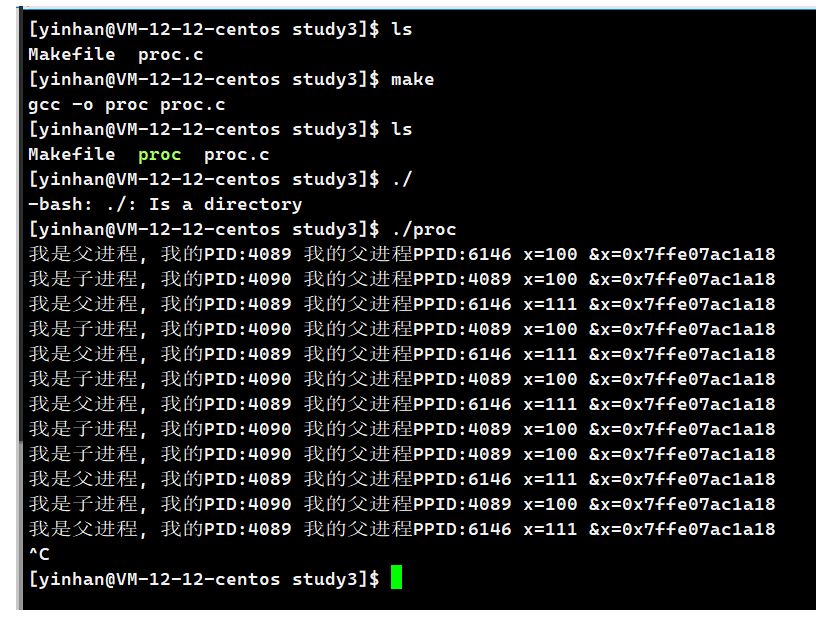
Linux进程概念(一)
文章目录Linux进程概念(一)1. 冯诺依曼体系结构2. 操作系统(Operator System)2.1 考虑2.2 如何理解操作系统对硬件做管理?2.3 操作系统为什么要对软硬件资源做管理呢?2.4 系统调用和库函数概念2.5 计算机体系结构3. 进程的初步理解…...
Leetcode.1124 表现良好的最长时间段
题目链接 Leetcode.1124 表现良好的最长时间段 Rating : 1908 题目描述 我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。 所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格…...

达梦数据库会话、事务阻塞排查步骤
查询阻塞的事务IDselect * from v$trxwait order by wait_time desc;--单机select * from v$dsc_trxwait order by wait_time desc;–DSC集群查询阻塞事务的会话信息select sf_get_session_sql(sess_id),* from v$sessions where trx_id69667;--单机select sf_get_session_sql(…...

sqlServer 2019 开发版(Developer)下载及安装
下载软件 官网只有2022的,2019使用百度网盘进行下载 安装下崽器 选择自定义安装 选择语言、以及安装位置 点击“安装” 安装 SQL Server 可能的故障 以上步骤安装后会弹出以上界面,如果未弹出,手动去安装目录下点击 SETUP.EXE 文件…...
使用Arthas定位问题
功能概述 首先,Arthas的常用功能大概有以下几个: 解决依赖冲突 sc命令:模糊查看当前 JVM 中是否加载了包含关键字的类,以及获取其完全名称。 sc -d 关键字 注意使用 sc -d 命令,获取 classLoaderHash命令:…...
性能测试之tomcat+nginx负载均衡
nginx tomcat 配置准备工作:两个tomcat 执行命令 cp -r apache-tomcat-8.5.56 apache-tomcat-8.5.56_2修改被复制的tomcat2下conf的server.xml 的端口号,不能与tomcat1的端口号重复,不然会启动报错 ,一台电脑上想要启动多个tomcat,…...
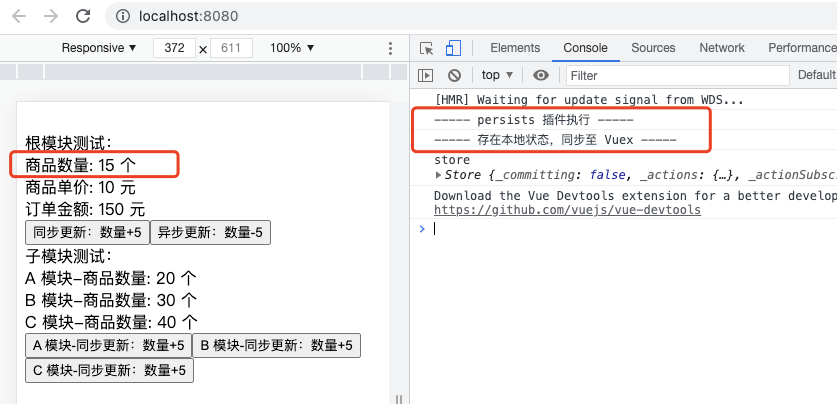
【手写 Vuex 源码】第十一篇 - Vuex 插件的开发
一,前言 上一篇,主要介绍了 Vuex-namespaced 命名空间的实现,主要涉及以下几个点: 命名空间的介绍和使用;命名空间的逻辑分析与代码实现;命名空间核心流程梳理; 本篇,继续介绍 Vu…...

opencv基础知识和绘图图形
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

15- 决策回归树, 随机森林, 极限森林 (决策树优化) (算法)
1. 决策回归树: from sklearn.tree import DecisionTreeRegressor model DecisionTreeRegressor(criterionmse,max_depth3) model.fit(X,y) # X是40个点 y是一个圆 2. 随机森林 稳定预测: from sklearn.ensemble import RandomForestClassifier # model RandomForestC…...

Flink相关的记录
Flink源码编译首次编译的时候,去除不必要的操作,同时install会把Flink中的module安装到本地仓库,这样依赖当前module的其他组件就无需去远程仓库拉取当前module,节省了时间。mvn clean install -T 4 -DskipTests -Dfast -Dmaven.c…...
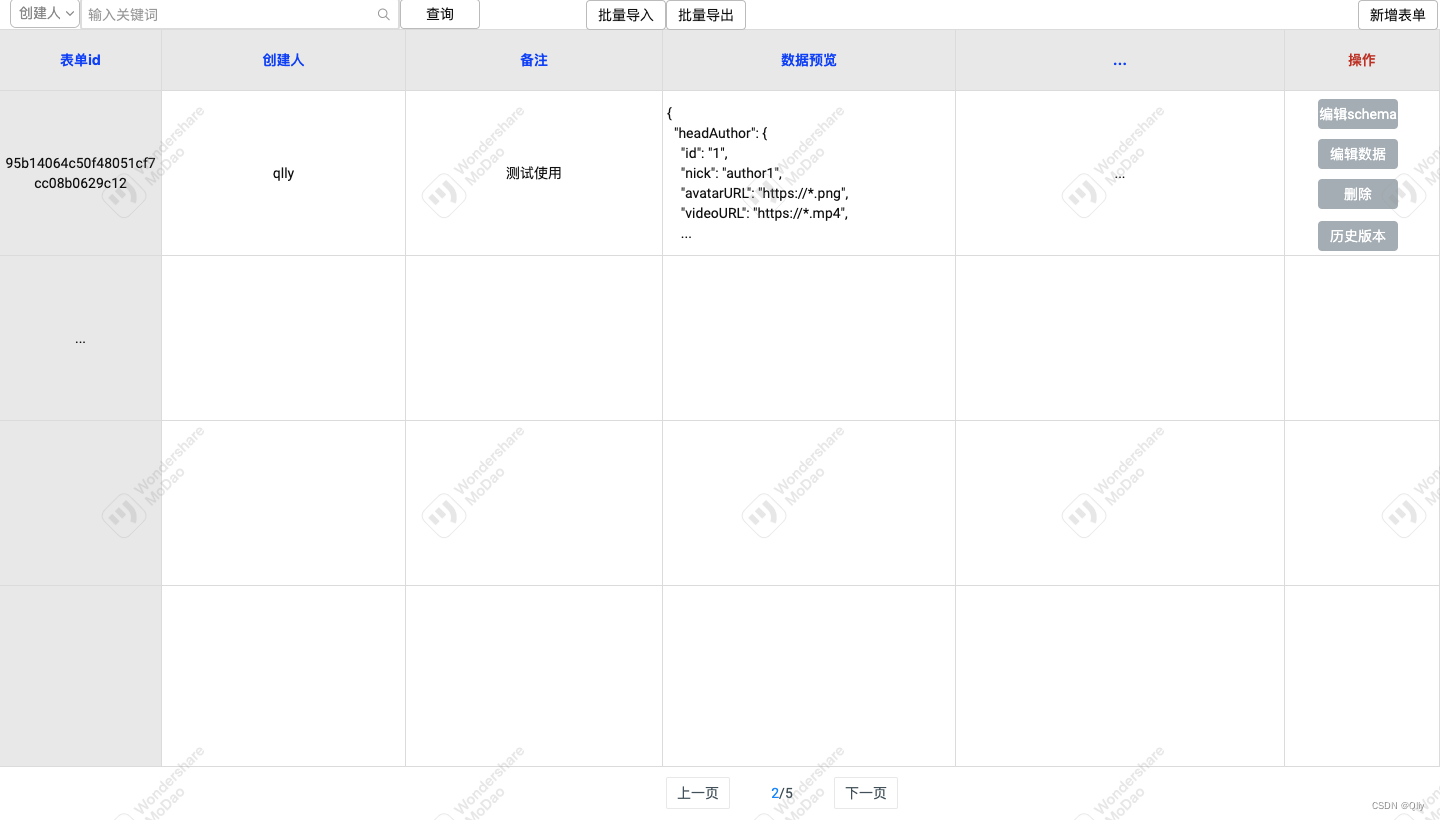
配置可视化-基于form-render的无代码配置服务(一)
背景 有些业务场景需要产品或运营去配置JSON数据提供给开发去使用(后面有实际业务场景的说明),原有的业务流程,非开发人员(后面直接以产品指代)把数据交给开发,再由开发去更新JSON数据。对于产…...
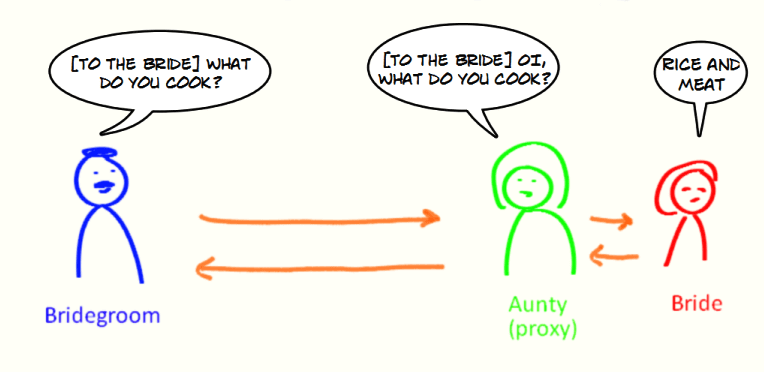
Java 代理模式详解
1、代理模式 代理模式是一种比较好理解的设计模式。简单来说就是 我们使用代理对象来代替对真实对象(real object)的访问,这样就可以在不修改原目标对象的前提下,提供额外的功能操作,扩展目标对象的功能。 代理模式的主要作用是扩展目标对象…...
知识付费小程序怎么做_分享知识付费小程序的作用
在线知识付费产业的主要业务逻辑是基于用户的主动学习需求,为其提供以跨领域基础知识与技能为核心的在线知识服务,提升其达到求知目的的效率。公众号和小程序的迅速发展,又为知识付费提供了技术支持,从而促进了行业的进一步发展。…...
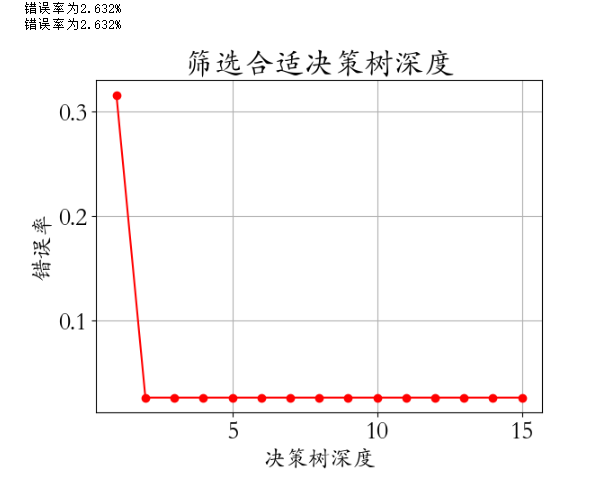
14- 决策树算法 (有监督学习) (算法)
决策树是属于有监督机器学习的一种决策树算法实操: from sklearn.tree import DecisionTreeClassifier # 决策树算法 model DecisionTreeClassifier(criterionentropy,max_depthd) model.fit(X_train,y_train)1、决策树概述 决策树是属于有监督机器学习的一种,起源…...

如何编译和运行C++程序?
C 和C语言类似,也要经过编译和链接后才能运行。在《C语言编译器》专题中我们讲到了 VS、Dev C、VC 6.0、Code::Blocks、C-Free、GCC、Xcode 等常见 IDE 或编译器,它们除了可以运行C语言程序,还可以运行 C 程序,步骤是一样的&#…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
