【scipy.sparse】diags()和dia_matrix()的区别
【scipy.sparse】diags()和dia_matrix()的区别
文章目录
- 【scipy.sparse】diags()和dia_matrix()的区别
- 1. 介绍
- 2. 代码示例
- 2.1 sp.diags()
- 2.1.1 第一种用法(data+offsets)
- 2.1.2 广播(需要指定shape)
- 2.1.3 只有一条对角线
- 2.2 sp.dia_matrix()
- 2.2.1 典型用法(与sp.diags()的这种用法相同、看上面2.1.1)
- 2.2.2 可能会混淆的用法
1. 介绍
经常遇到sp.diags() 和 sp.dia_matrix(), 还傻傻分不清楚。
- sp.diags() 是对角的元素,这个对角的元素有三个,每一个都是一个列表形式,它的用途要比sp.dia_matrix()的多,具体的一会儿看例子。
- sp.dia_matrix通过两个数组确定: data和offsets。其中data对角线元素的值;offsets:第i个offsets是当前第i个对角线和主对角线的距离。data[k:]存储了offsets[k]对应的对角线的全部元素。
2. 代码示例
2.1 sp.diags()
2.1.1 第一种用法(data+offsets)
- 第一个参数的第一个元素是[1,2,3,4],对应的第2个参数的数是0(相当于主对角线偏移为0,其实就是主对角线),所以1,2,3,4放在主对角线位置。
- 第1个参数的第2个元素是[1,2,3],对应的第2个参数的数是-1,所以1,2,3放在主对角线靠下偏1的对角线位置。
- 第1个参数的第三个元素是[1,2],对应的第2个参数的数是2,所以1,2放在主对角线靠上偏2的对角线位置。
- 其余地方补0就好。因为对角矩阵肯定是个方阵,所以就最后就是4*4的方阵。
>>> data = [[1, 2, 3, 4], [1, 2, 3], [1, 2]]
# 使用diags函数,该函数的第二个变量为对角矩阵的偏移量,
0:代表不偏移,就是(0,0)(1,1)(2,2)(3,3)...这样的方式写
k:正数:代表像正对角线的斜上方偏移k个单位的那一列对角线上的元素。
-k:负数,代表向正对角线的斜下方便宜k个单位的那一列对角线上的元素,>>> diags(data, [0, -1, 2]).toarray()
array([[1, 0, 1, 0],[1, 2, 0, 2],[0, 2, 3, 0],[0, 0, 3, 4]])
2.1.2 广播(需要指定shape)
# 这种情况可以广播(其实就是每个对角线的元素是相同的),但需要指定矩阵大小。>>> diags([1, -2, 1], [-1, 0, 1], shape=(4, 4)).toarray()
array([[-2., 1., 0., 0.],[ 1., -2., 1., 0.],[ 0., 1., -2., 1.],[ 0., 0., 1., -2.]])
2.1.3 只有一条对角线
# 指定offset为1
>>> diags([1, 2, 3], 1).toarray()
array([[ 0., 1., 0., 0.],[ 0., 0., 2., 0.],[ 0., 0., 0., 3.],[ 0., 0., 0., 0.]])# 不指定offsets的话,默认为0
>>> diags([1, 2, 3, 4]).toarray()
array([[ 1., 0., 0., 0.],[ 0., 2., 0., 0.],[ 0., 0., 3., 0.],[ 0., 0., 0., 4.]])
2.2 sp.dia_matrix()
sp.dia_matrix()的用法比较单一。注意:与sp.diags()记混则会出现错误的结果。
2.2.1 典型用法(与sp.diags()的这种用法相同、看上面2.1.1)
>>> data = np.array([[1, 2, 3, 4], [5, 6, 0, 0], [0, 7, 8, 9]])
>>> offsets = np.array([0, -2, 1])
>>> dia_matrix((data, offsets), shape=(4, 4)).toarray()
array([[1, 7, 0, 0],[0, 2, 8, 0],[5, 0, 3, 9],[0, 6, 0, 4]])
2.2.2 可能会混淆的用法
# 注意这种用法不会产生如2.1.3的情况,而是出现下面的结果:
>>> dia_matrix([1,2,3]).toarray()
array([[1, 2, 3]])
对于sp.dia_matrix(),其他的用法,则会报错。
相关文章:
和dia_matrix()的区别)
【scipy.sparse】diags()和dia_matrix()的区别
【scipy.sparse】diags()和dia_matrix()的区别 文章目录【scipy.sparse】diags()和dia_matrix()的区别1. 介绍2. 代码示例2.1 sp.diags()2.1.1 第一种用法(dataoffsets)2.1.2 广播(需要指定shape)2.1.3 只有一条对角线2.2 sp.dia_…...
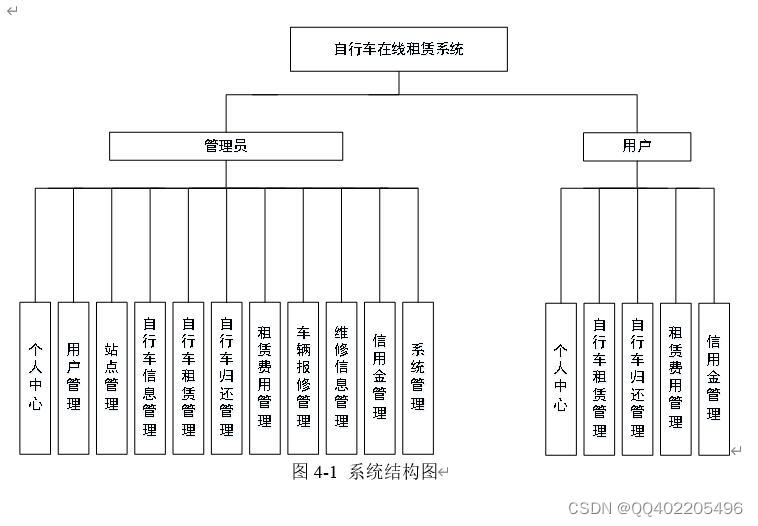
java ssm自行车在线租赁系统idea
当前自行车在社会上广泛使用,但自行车的短距离仍旧不能完全满足广大用户的需求。自行车在线租赁系统可以为用户提供租赁用车等功能,拥有较好的用户体验.能实时在线租赁提供更加快捷方便的租车方式,解决了常见自行车在线租赁系统较为局限的自行车归还功能。 通过使用本系统&…...

GAN和CycleGAN
文章目录1. GAN 《Generative Adversarial Nets》1.1 相关概念1.2 公式理解1.3 图片理解1.4 熵、交叉熵、KL散度、JS散度1.5 其他相关(正在补充!)2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Ne…...
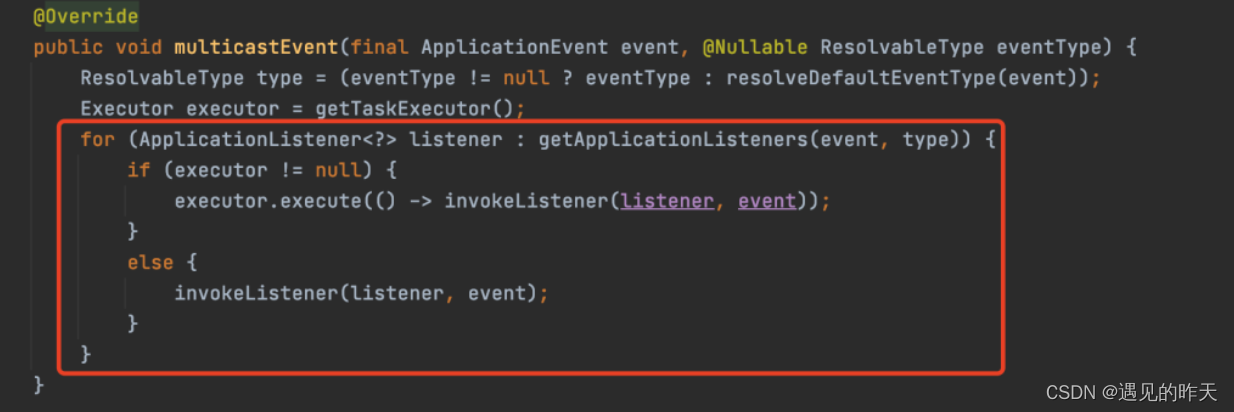
源码项目中常见设计模式及实现
原文https://mp.weixin.qq.com/s/K8yesHkTCerRhS0HfB0LeA 单例模式 单例模式是指一个类在一个进程中只有一个实例对象(但也不一定,比如Spring中的Bean的单例是指在一个容器中是单例的) 单例模式创建分为饿汉式和懒汉式,总共大概…...
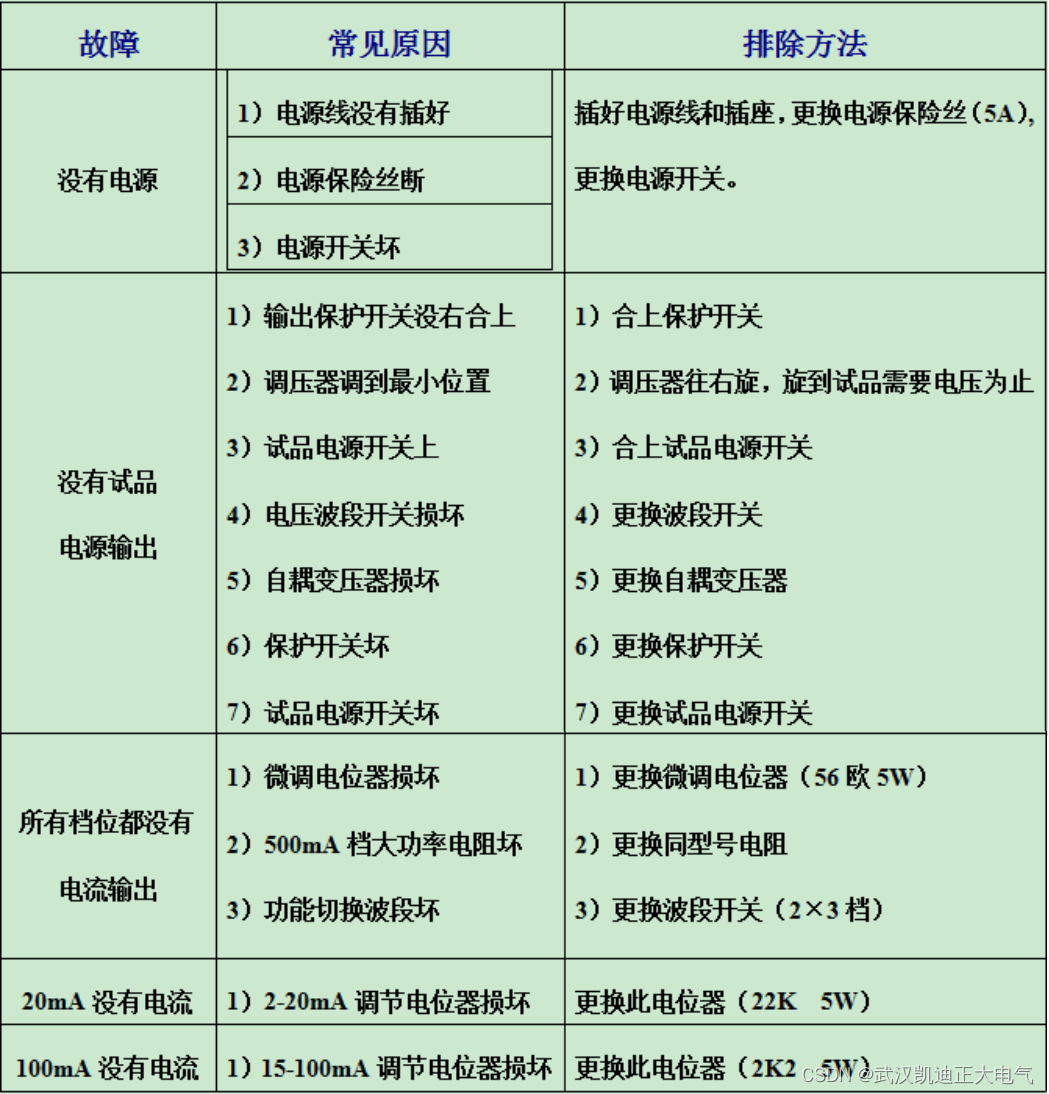
KDNM5000-10A-2剩余电流保护器测试仪
一、产品概述 KDNM5000-10A-2型剩余电流保护器测试仪(以下简称测试仪),是本公司改进产品,是符合国家标准《剩余电流动作保护器》(GB6829—95)中第8.3条和GB16917.1—1997中第9.9条验证AC型交流脱扣器动作特性要求的专用测试仪器。…...

C++实现线程池
C实现线程池一、前言二、线程池的接口设计2.1、类封装2.2、线程池的初始化2.3、线程池的启动2.4、线程池的停止2.5、线程的执行函数run()2.6、任务的运行函数2.7、等待所有线程结束三、测试线程池四、源码地址总结一、前言 C实现的线程池,可能涉及以下知识点&#…...
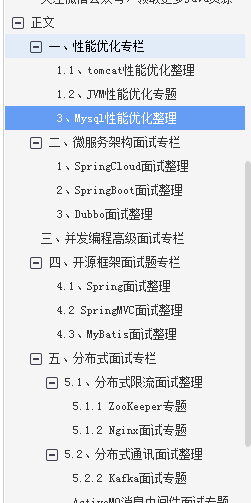
2023最新Java面试手册(性能优化+微服务架构+并发编程+开源框架)
Java面试手册 一、性能优化面试专栏 1.1、 tomcat性能优化整理 1.2、JVM性能优化整理 1.3、Mysql性能优化整理 二、微服务架构面试专栏 2.1、SpringCloud面试整理 2.2、SpringBoot面试整理 2.3、Dubbo面试整理 三、并发编程高级面试专栏 四、开源框架面试题专栏 4.1、Sprin…...

对灵敏度分析技术进行建模(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
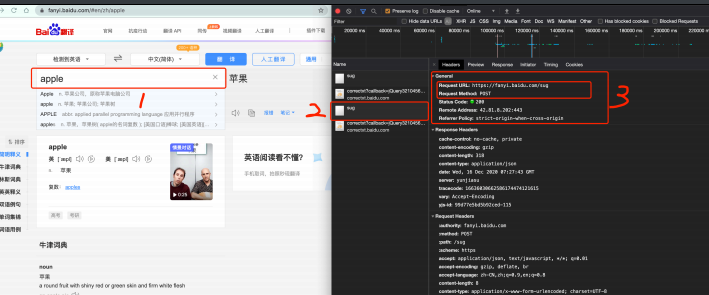
完整爬虫学习笔记(第一章)
文章目录前言:fu:. 爬虫概述:hotdog:原理解剖:one: 服务器渲染:two: 前端JS渲染:fire: 第一个爬虫程序案例总结前言 最近正在学习Python网络爬虫的相关知识,鉴于本人Python水平有限 , 对Python并无太深的理解,所以此文章的主要目的在于抛砖引玉…...
会计师项目管理软件是什么,哪些必不可少的功能
欢迎阅读现代金融专业人士的会计师项目管理指南。在本文中,我们将深入探讨在基于项目的会计的各个方面使用项目管理方法的好处。我们还将教您面临哪些挑战以及如何为您的团队选择最佳工具。 为什么会计师的项目管理很重要? 在会计方面,目标始…...

第 8 章 优化
目录 8.1 优化概述 8.2 优化 SQL 语句 8.3 优化和指标 8.4 优化数据库结构 8.5 优化 InnoDB 表 8.6 优化 MyISAM 表 8.7 内存表的优化 8.8 了解查询执行计划 8.9 控制查询优化器 8.10 缓冲和缓存 8.11 优化锁定操作 8.12 优化 MySQL 服务器 8.13 衡量性能ÿ…...

剑指offer -- java题解
剑指offer -- java题解刷题地址1、数字在升序数组中出现的次数2、二叉搜索树的第k个节点3、二叉树的深度4、数组中只出现一次的两个数字5、和为S的两个数字6、左旋转字符串7、滑动窗口的最大值8、扑克牌顺子9、孩子们的游戏(圆圈中最后剩下的数)10、买卖股票的最好时机(一)刷题…...

若依ruoyi——手把手教你制作自己的管理系统【二、修改样式】
阿里图标一( ̄︶ ̄*)) 图片白嫖一((* ̄3 ̄)╭ ********* 专栏略长 爆肝万字 细节狂魔 请准备好一键三连 ********* 运行成功后: idea后台正常先挂着 我习惯用VScode操作 当然如果有两台机子 一个挂后台一个改前端就更好…...

2023.2.14每日一题——455. 分发饼干
每日一题题目描述解题核心解法一:双指针题目描述 题目链接:455. 分发饼干 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],…...

MySQL入门篇-MySQL常用字符函数小结
备注:测试数据库版本为MySQL 8.0 这个blog我们来聊聊常见的字符函数 函数名函数用途UPPER()返回大写的字符LOWER()返回小写的字符LTRIM()左边去掉空格TRIM()去掉空格RTRIM()右边去掉空格SPACE()返回指定长度的空格CONCAT()连接字符串CONCAT_WS()指定分隔符连接字符串CHAR_LEN…...
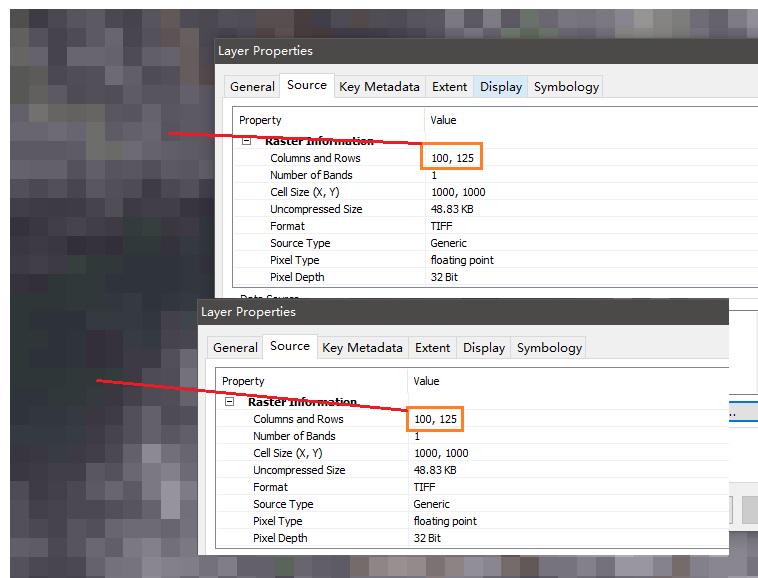
解决不同影像裁剪后栅格数据行列不一致问题
前言在处理栅格数据时,尽管用同一个矢量文件裁剪栅格数据,不同数据来源的栅格行列数也会出现不一致的情况。如果忽略或解决不好,会导致后续数据处理出现意想不到的误差或错误,尤其是利用编程实现数据处理时。因此,应当…...
visual studio2022配置opencv
标题:在vs下配置使用opencv 流程: 1、下载安装opencv 2、添加环境变量 3、vs中配置属性 4、使用 5、可能遇到的报错和解决 1、 下载安装opencv 官网下载地址: https://opencv.org/releases/ 我这里是windows环境,所以选择点击w…...

什么是销售管理?销售管理的五大职能
销售管理听起来很简单,似乎只是负责销售并确保客户满意,但事实上,它远不止于此。 销售管理的实际职能包括监督销售团队的工作,制定计划和设定目标,通常还包括确保销售流程的效率以获得最佳业务结果。 什么是销售管理…...

[CVPR‘22] EG3D: Efficient Geometry-aware 3D Generative Adversarial Networks
paper: https://nvlabs.github.io/eg3d/media/eg3d.pdfproject: EG3D: Efficient Geometry-aware 3D GANscode: GitHub - NVlabs/eg3d总结: 本文提出一种hybrid explicit-implicit 3D representation: tri-plane hybrid 3D representation,该方法不仅有…...

Learning C++ No.9【STL No.1】
引言: 北京时间:2023/2/13/18:29,开学正式上课第一天,直接上午一节思想政治,下午一节思想政治,生怕我们……,但,我深知该课的无聊,所以充分利用时间,把我的小…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
