动态规划详解(完结篇)——如何抽象出动态规划算法?以及解题思路
今天直接开始讲解
FIRST:如何抽象出动态规划算法?
这个问题,困扰了无数代OIER,包括本蒟蒻
在比赛的时候,看一道题,怎么想到他是什么算法的呢?
这就需要抽象能力
而不同的算法,往往有着不同的特点
就来说说动态规划的题目特点
通过遍历,能够把所有的情况考虑到。这一点同样适合于递归
有可能存在重叠性的子问题。没错,这一点也适用于递归
有的同学就问了
那动态规划和递归不是同样的特点吗?

回到蒟蒻写的动态规划1
里面说过,动态规划是可以用递归代替的
也就是说,如果你的状态转移方程真的实在绞尽脑汁费劲九牛二虎之力也想不出来,就用递归来做
但代价就是也许拿不到满分
SECOND:解题思路
动态规划抽象出状态之后,就要进行遍历每一个状态
抽象状态
初始化
确定循环起始以及边界
写出状态转移方程
输出
return 0;
大概就是上述这个过程了
每日例题:
题目描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有 22 个整数 �T(1≤�≤10001≤T≤1000)和 �M(1≤�≤1001≤M≤100),用一个空格隔开,�T 代表总共能够用来采药的时间,�M 代表山洞里的草药的数目。
接下来的 �M 行每行包括两个在 11 到 100100 之间(包括 11 和 100100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出在规定的时间内可以采到的草药的最大总价值。
输入输出样例
输入 #1复制
70 3 71 100 69 1 1 2
输出 #1复制
3
说明/提示
【数据范围】
对于 30%30% 的数据,�≤10M≤10;
对于全部的数据,�≤100M≤100。
一个纯纯的01背包模板
抽象状态:f[i]表示第i分钟采到的最大价值
初始化:no
确定循环起始以及边界:第一层循环1到m,第二层循环t到0(真的是01背包模板,看不懂的可以借鉴一下上一篇文章)
写出状态转移方程:dp[j]=max(dp[j-w[i]]+val[i], dp[j]);如果采了这个药,那么就要用当前时间减去采药的时间,也就是采药之前需要的时间加上现在的状态
输出(见代码)
真正做题时,大家也可以按照这个顺序,非常的清晰
那么有的同学就要问了:状态定义有什么规律吗?
首先,我们先创建一个数组,f数组,假设他是一维的,然后去想这个一维状态表示什么(简单多了)
就假设是一维,尝试写状态转移方程
如果发现,写不通了,也就是有更多的情况表示不出来
增加维度
然后循环上述操作
但是遇到很难的题,还得是靠智商,因为难的动态规划不仅仅要抽象出来
更需要你优化,也就是减少维度
来迟的AC代码:
# include <iostream>
# include <cstdio>
using namespace std;
int w[105], val[105];
int dp[1005];
int main(){int t,m; scanf("%d%d",&t,&m);for(int i=1;i<=m;i++){scanf("%d%d",&w[i],&val[i]);}for(int i=1;i<=m;i++) {for(int j=t;j>=0;j--) {if(j>=w[i]){dp[j]=max(dp[j-w[i]]+val[i], dp[j]);}}} printf("%d",dp[t]);return 0;
}这会动态规划系列就真的结束了
这次讲算法比之前真的费了更大的力气,更多的时间,更多的键盘()
所以希望各位佬能够点个免费的赞
如果动态规划方面还有什么不明白的,随时私信我
我可以出番外篇()
这篇文章到这里就结束了
再见
相关文章:

动态规划详解(完结篇)——如何抽象出动态规划算法?以及解题思路
今天直接开始讲解FIRST:如何抽象出动态规划算法?这个问题,困扰了无数代OIER,包括本蒟蒻在比赛的时候,看一道题,怎么想到他是什么算法的呢?这就需要抽象能力而不同的算法,往往有着不同…...
C语言一维数组篇【下】——每日刷题经验分享
一维数组篇——每日刷题经验分享~😎前言🙌有序序列插入一个整数 😊序列中删除指定数字 😊序列中整数去重小乐乐查找数字筛选法求素数总结撒花💞😎博客昵称:博客小梦~ 😊最喜欢的座右…...

VHDL语言基础-组合逻辑电路-其它组合逻辑模块
目录 多路选择器: 逻辑功能: 常用的类型: 4选1多路选择器的实现: 求补器: 求补器的实现: 三态门: 三态门的应用实例: 三态门的实现: 缓冲器: 什么是…...

初识Vue
文章目录1. 前言2. Vue 的特点3. 安装 Vue4. HelloWord1. 前言 vue是什么 ? 引用 : vue.js 文档 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。与其它大型框架不同的是,Vue 被设计为可以自底向上逐层…...

TOUGH系列软件建模实践方法及在地下水、CO2地质封存、水文地球化学、地热等多相多组分系统多过程耦合
查看原文>>> https://mp.weixin.qq.com/s?__bizMzAxNzcxMzc5MQ&mid2247578057&idx7&sn75f8d2c1c6edb28af76a8db4bb773de3&chksm9be2aed9ac9527cf0081082cdcf781e6c37f9f3ba383332ed1116abcbee0f05c0593187e964d&token2070450548&langzh_CN#r…...

Codeforces Round #699 (Div. 2)
E. 题意:n本书,每本书有颜色a[i],一次操作可以将其中一本书放在末尾,求满足:相同颜色的书都是相邻的 的最小操作次数. 显然最多只需要n次,考虑能节省多少次.倒着考虑,记f[i]为i~n最多能节约的次数.先预处理出每种颜色的出现的位置范围l[i],r[i]. 1.不节约这本书f[i] f[i 1]…...

MySQL存储过程的传参和流程控制
目录 一.存储过程传参—in 演示 二.存储过程传参—out 演示 三.存储过程传参—inout 演示 四.流程控制—判断 格式 演示 五.流程控制—case 语法 演示 六.流程控制—循环 循环—while 循环—repeat 循环—loop 一.存储过程传参—in in表示传入的参数,可以传…...
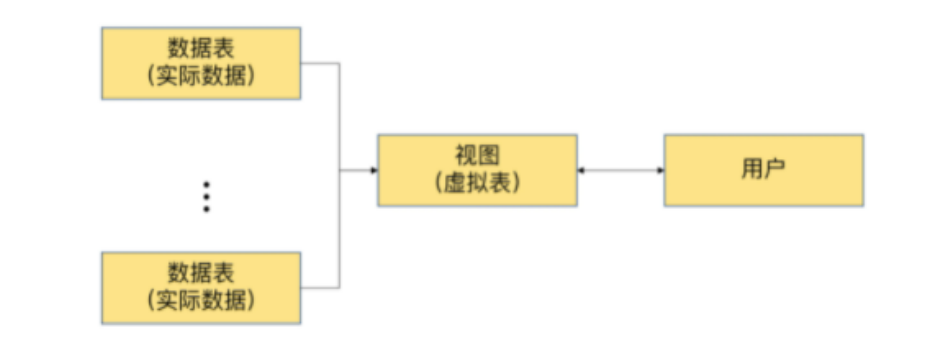
MySQl学习(从入门到精通11)
MySQl学习(从入门到精通11)第 14 章_视图1. 常见的数据库对象2. 视图概述2. 1 为什么使用视图?2. 2 视图的理解3. 创建视图3. 1 创建单表视图3. 2 创建多表联合视图3. 3 基于视图创建视图4. 查看视图5. 更新视图的数据5. 1 一般情况5. 2 不可…...

关于ThreadLocal
弱引用 1.1 java中的各种引用和测试: https://blog.csdn.net/thewindkee/article/details/102723838 1.2 treadlocal中的弱引用测试: https://blog.csdn.net/thewindkee/article/details/103726942 (这篇很重要) 内存泄露: https://zhuanlan.zhihu.com/p/523628871 综合考虑 …...

【C++】类和对象(中)
文章目录1. 类的6个默认成员函数2. 构造函数概念特性3. 析构函数概念特性4. 拷贝构造函数概念特征5. 运算符重载5.1 前置和后置重载5.2 赋值运算符重载6. 日期类的实现7. const成员8. 取地址及const取地址操作符重载1. 类的6个默认成员函数 如果一个类中什么成员都没有&#x…...

js下载文件
url为文件的src地址 url必须符合同源策略或者url的接口地址允许跨域,否则浏览器会报跨域错误 axios.get(data.url ,{ responseType: ‘blob’, }) .then( response>{ let blob new Blob([response.data]); let url window.URL.createObjectURL(blob); // 创建 …...

ESP8266 + STC15+ I2C OLED带网络校时功能的定时器时钟
ESP8266 + STC15+ I2C OLED带网络校时功能的定时器时钟 📍相关篇《ESP8266 + STC15基于AT指令通过TCP通讯协议获取时间》 📌ESP8266 AT固件基于安信可AT固件,相关刷AT固件可以参考《NodeMCU-刷写AT固件》 🔖STC15 单片机采用的是:STC15F2K60S2 晶振频率采用内部:22.11…...

计算机入门基础知识大全
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的,绽…...

Python程序出现错误怎么办?
Python 异常处理 python提供了两个非常重要的功能来处理python程序在运行中出现的异常和错误。你可以使用该功能来调试python程序。 异常处理: 本站Python教程会具体介绍。 断言(Assertions):本站Python教程会具体介绍。 python标准异常 异常名称 描述 BaseException 所有异常…...

【Vue3】v-if和v-for优先级
🎈博客主页:🌈我的主页🌈 🎈欢迎点赞 👍 收藏 🌟留言 📝 欢迎讨论!👏 🎈本文由 【泠青沼~】 原创,首发于 CSDN🚩…...

Windows上实现 IOS 自动化测试
本文介绍如何使用tideviceWDAairtest/facebook-wda实现在Windows上进行IOS APP自动化测试 环境准备 Windows Python环境 Python 3.6 WebDriverAgent安装 下载最新的项目到Mac:https://github.com/appium/WebDriverAgent $ git clone https://github.com/appiu…...
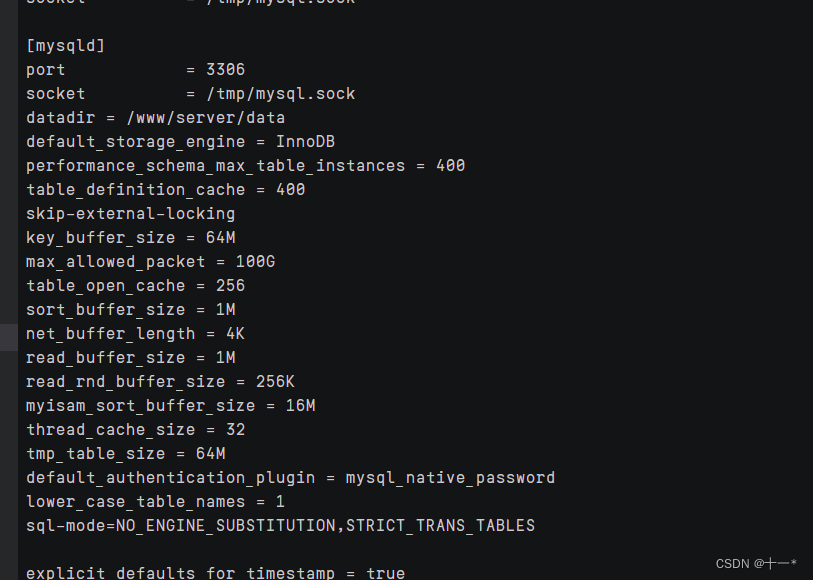
Linux云服务器下怎么重置MySQL8.0数据库密码
文章目录一、修改my.cnf配置文件为mysql免登陆二、免密登陆mysql三.给root用户重置密码1、首先查看当前root用户相关信息,在mysql数据库的user表中2、把root密码置为空3、退出mysql,删除/etc/my.cnf文件中添加进去的skip-grant-tables 重启mysql服务4、使…...
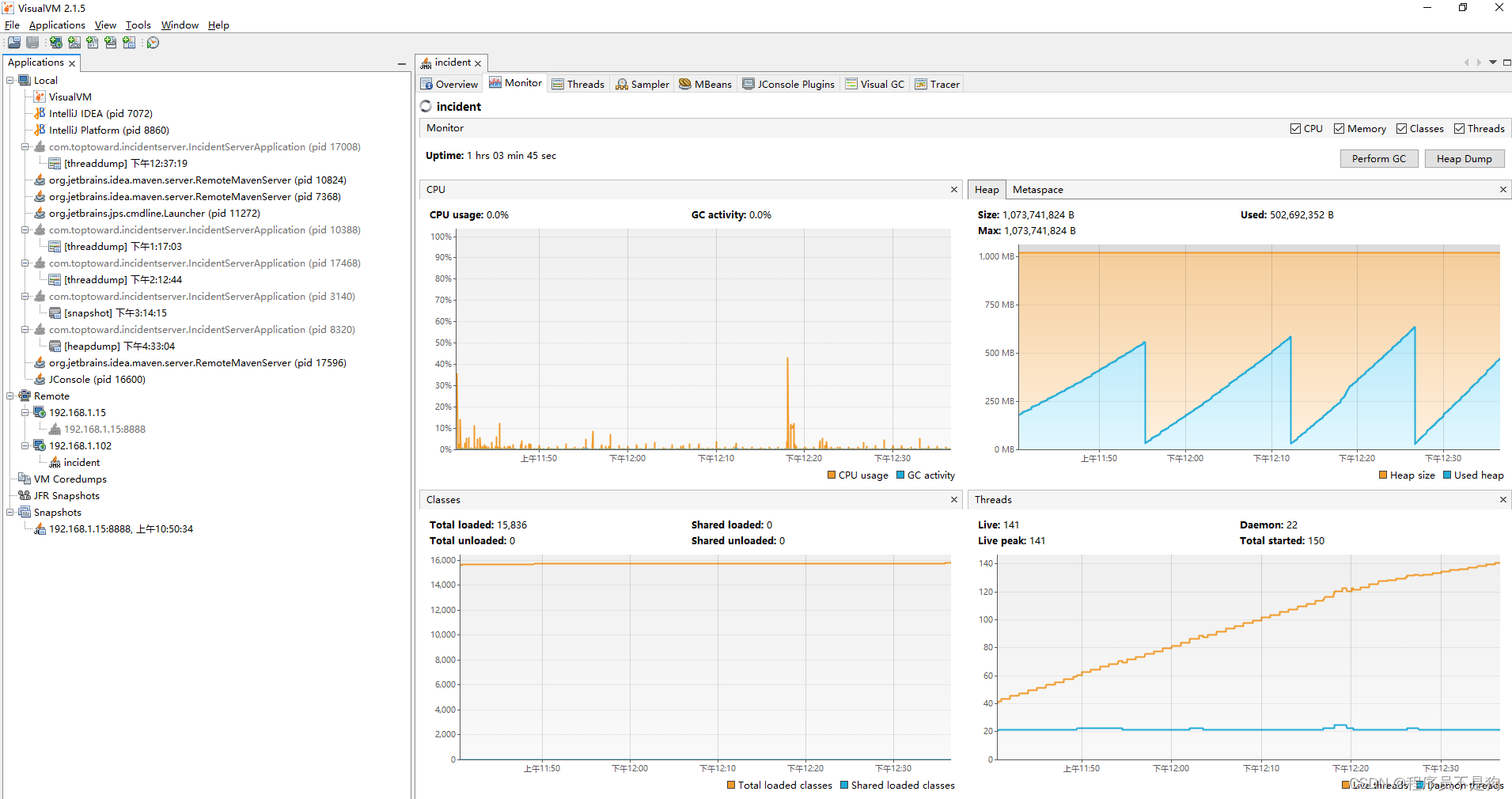
JVM调优
JVM调优-VisualVmVisualVm/ Jconsule远程连接第一种方式第二种方式:java 11开启远程GC连接如果还连不上考虑防火墙拦截了端口firewall-cmd --list-all,查看一下并暴露对应端口连接配置VisualVm界面简介采集GC信息的一些命令垃圾回收器切换VisualVm/ Jconsule远程连接…...
【配电网规划】SOCPR和基于线性离散最优潮流(OPF)模型的配电网规划( DNP )(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

锦正茂EM3电磁铁的技术参数
产品特点: ※U形结构、视野开阔、磁场强度高、磁场强度大小调节方便 ※体积小、重量轻、占空比小、结构紧凑、磁场性能更佳 ※电磁铁的工作气隙调节轻便灵活,极头处设有螺纹,更换极头装卸方便 ※可选配工作间隙刻度指示 ※小气隙时用于铁…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
