浅谈软件测试需求管理
什么是需求管理?
需求管理,指对产品、系统或工程的开发需求的搜集、定义、分析、评审、整理、维护、追溯和复用等相关的管理工作和流程。通常特指应用程序或软件系统的研发需求。需求管理和配置管理、测试管理、缺陷管理、风险管理、变更管理等管理流程一起构成了ALM应用全生命周期管理的完整流程。需求管理过程定义并逐层分解了整个应用的功能和相关限制条件,以及管理随着开发过程迭代所产生的上下游的追溯关系,最终保证发布的产品与最初设计需求之间的一致性。
需求管理是系统研发过程中不必可少的环节,在实际的研发项目中,需求管理所涉及的工作一般会包括:
- 需求的收集和定义
- 需求的导入导出
- 需求的分解和细化
- 需求的评审
- 需求的发布
- 需求的变更
- 需求的追溯
- 需求的复用
- 对需求的测试等
为什么要做需求管理?
一般的项目通常会有大量的设计需求,尤其是有高安全性相关要求的项目。这些需求会列在不同的需求文档,如产品需求,系统需求,软件/硬件/机械需求等。若是不将这些大量的需求进行管理,用户是无法清楚了解到需求是否被满足,需求是否被测试用例所验证,需求是否是进过讨论–需求是否需要修改/调整,然后再次经过流程确认调整后的需求是否被其他团队的认可(例如,是否有开发/技术上的困难)。若是一个项目没有一个好的需求管理系统和流程,项目的生命周期会延长,用户也没有一个很好的平台来看到整个项目的一个状态。
简单地说,需求管理的目的是为了建立一种基于需求的覆盖应用全生命周期的有序追溯关系,保证最终发布的产品不会偏离原本的期望。具体体现在:
- · 所有的上层产品需求在分解、开发和测试的过程中没有被遗漏
- · 没有出现意料之外的需求
- · 一目了然的变更影响分析保证了研发流程信息的同步。产品研发的迭代过程中,任一层级的需求的变更所造成的影响都能被及时地发现,并对上下游的需求进行更新和维护
- · 利用合理的评审流程减少了错误的、模糊的或不合理的需求的出现,降低了因为需求的质量导致的产品缺陷的风险
需求管理的工作可以是通过Word,Excel等文档由产品研发人员来管理,也可以是借助现成的需求管理工具来完成。而随着企业业务的扩大和产品复杂度的升高,人工管理变得越来越困难,人们需要一种更为高效的、行之有效的管理手段,来实现对需求的有序管理。
最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:

这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴上万个测试工程师们走过最艰难的路程,希望也能帮助到你!有需要的小伙伴可以点击下方小卡片领取
相关文章:

浅谈软件测试需求管理
什么是需求管理? 需求管理,指对产品、系统或工程的开发需求的搜集、定义、分析、评审、整理、维护、追溯和复用等相关的管理工作和流程。通常特指应用程序或软件系统的研发需求。需求管理和配置管理、测试管理、缺陷管理、风险管理、变更管理等管理流程…...

面试题复盘
Vuex与本地存储的区别Vuex是一个专门为Vue.js应用程序开发的状态管理模式和库。它提供了一个中央存储库,用于存储应用程序的所有组件之间共享的状态【组件间通信的一种方法,一般用于中大型应用】。Vuex的主要目的是在Vue.js应用程序中管理复杂的状态逻辑…...

Telerik UI for WPF 2023 R1
Telerik UI for WPF 2023 R1 之 WPF 的 Telerik 用户界面,WPF 控件库开发人员信任,快速构建美观、高性能的 WPF 业务应用程序。现在支持 .NET 6 和 7.0。 概述部分背景图像 主要特征 现代专业主题图标,现代专业主题 通过各种受 Office、Wind…...
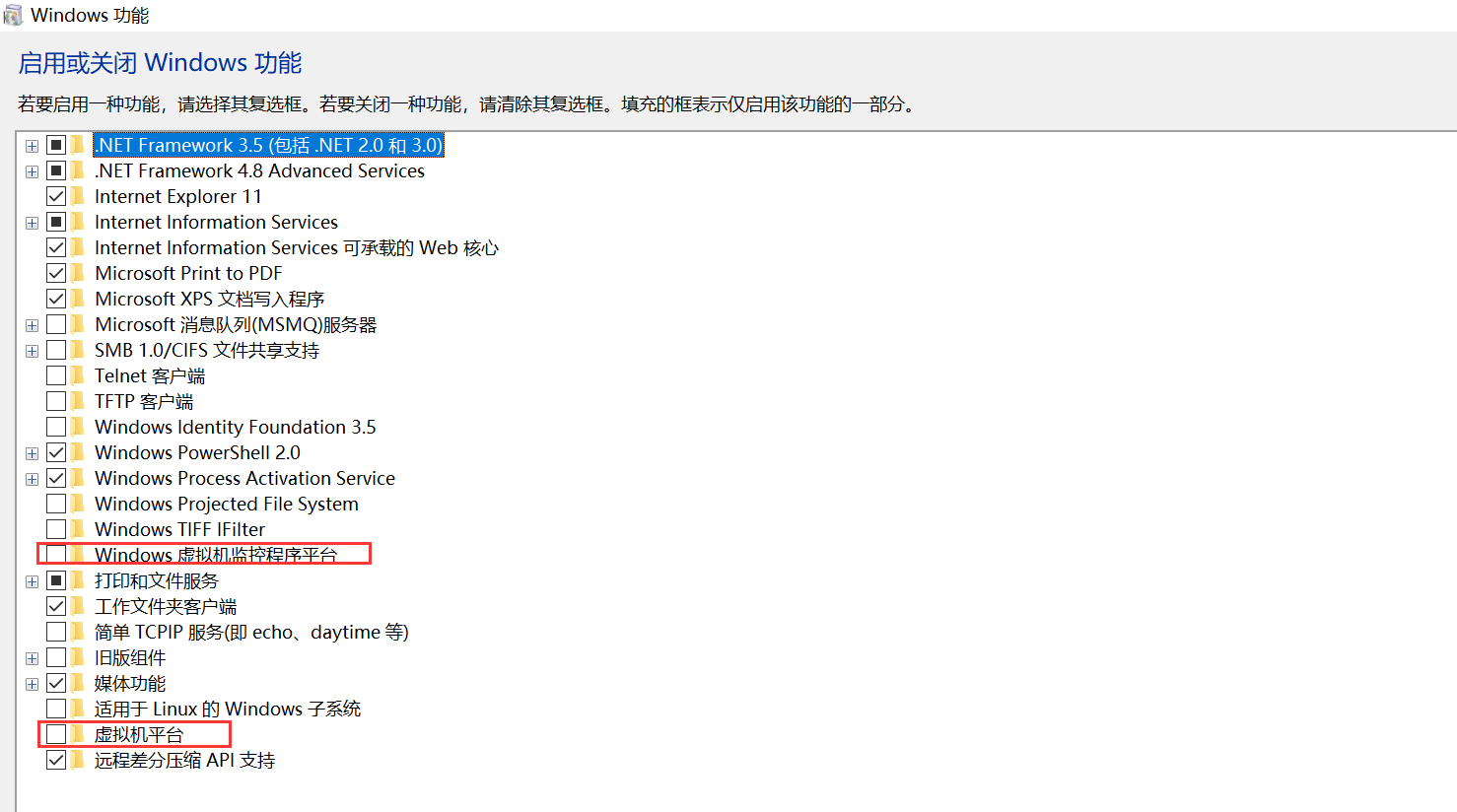
基于 CentOS7 的 KVM 部署 + 虚拟机创建
目录一、实验环境二、部署 KVM三、创建虚拟机四、远程管理 KVM 虚拟机FAQ一、实验环境 实验环境:VMware Workstation 16 Pro 打开虚拟机之前,首先开启 VMware Workstation Pro 16 上的硬件辅助虚拟化功能,如下图所示: 二、部署 …...

Python自动化测试实战篇(5)优化selenium+unittest+ddt,搞定100条测试用例只执行前50条
这些是之前的文章,里面有一些基础的知识点在前面由于前面已经有写过,所以这一篇就不再详细对之前的内容进行描述 Python自动化测试实战篇(1)读取xlsx中账户密码,unittest框架实现通过requests接口post登录网站请求&…...

C语言--数据的存储2
目录前言练习有符号类型与无符号类型char类型的取值范围有符号char无符号char有符号与无符号类型混合运算有符号无符号类型形成的bugchar类型取值范围应用浮点型在内存中的存储浮点数的存储浮点数存储规则浮点数取出规则前言 上篇文章我们讲解了数据类型,类型的基本…...

Ubuntu 安装 Qt5.7.0
下载 地址:https://download.qt.io/https://download.qt.io/ 文件夹说明: snapshots:预览版,该文件夹中包含最新的测试版本。 online:在线安装包。 official_releases:最终发布版。 new_archive&#…...
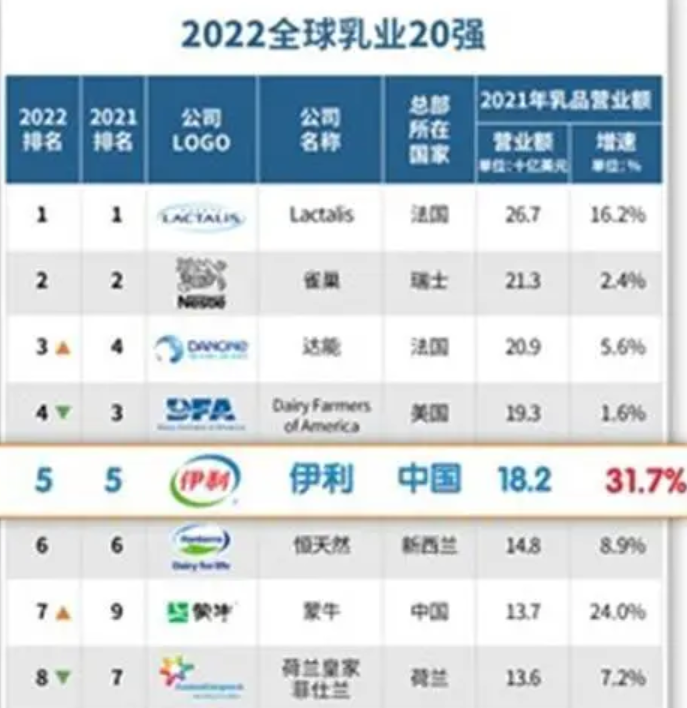
“世界”的伊利,“三难”的潘刚
(图片来源于网络,侵删) 来源 | 螳螂观察 文 | 叶小安 一棵草,一头牛,到一杯牛奶,乳品如何守住舌尖上的安全? 央视财经频道专访中,伊利集团董事长兼总裁潘自信满满地介绍了现代智…...
)
【新】华为OD机试 - 开心消消乐(Python)
开心消消乐 题目 给定一个 N 行 M 列的二维矩阵,矩阵中每个位置的数字取值为 0 或 1,矩阵示例如: 1 1 0 0 0 0 0 1 0 0 1 1 1 1 1 1现需要将矩阵中所有的 1 进行反转为 0,规则如下: 当点击一个 1 时,该 1 被反转为 0,同时相邻的上、下、左、右,以及左上、左下、右上…...

山东大学2022-2023数据仓库挖掘期末考题回忆
2023.2.14 一、 1.数据预处理的过程和解决问题 2.什么是离群点,检测离群点的四个方法 3.数据仓库的四个特点,画出数据仓库结构图 4.维度归约的两个方法及区别。 二、 两个模型用来预测新冠病毒的阳性和阴性 1.分别求准确率,精确率,…...

SSM整合
SSM整合 ContextLoaderListener Spring提供了监听器ContextLoaderListener,实现ServletContextListener接口,可监听 ServletContext的状态,在web服务器的启动,读取Spring的配置文件,创建Spring的IOC容器。 web 应用中…...

Android平台版本所对应的 API 级别
平台版本API级别版本号备注Android 1333TIRAMISU平台亮点Android 1232S_V2平台亮点31S平台亮点Android 1130R平台亮点Android 1029Q平台亮点Android 928P平台亮点Android 8.127O_MR1平台亮点Android 8.026O平台亮点Android 7.1.1Android 7.125N_MR1平台亮点Android 7.024N平台亮…...
入职字节外包一个月,我离职了
有一种打工人的羡慕,叫做“大厂”。 真是年少不知大厂香,错把青春插稻秧。 但是,在深圳有一群比大厂员工更庞大的群体,他们顶着大厂的“名”,做着大厂的工作,还可以享受大厂的伙食,却没有大厂…...

中创教育PMP分享,复盘没效果?该怎么办
复盘的清单框架 一、现在情况如何 二、当初是怎么决定的 三、让我们再审视下思考的前提 四、复盘他人 复盘没效果,我们可以试试下面的提问: 一、现在情况如何 现在做到什么程度? 当时定的目标是多少? 现在的结果和目标对比处于什么状态? 有没…...

Kubelet监控指标说明
Probe路径 含义:kubelet以及kubelet监控的Pod的存活性请求路径:“/metrics/probes”指标 名称类型含义upGauge服务是否存活prober_probe_totalCounter按结果计算容器的活动探测、就绪探测或启动探测的累计数目以及存活性结果 Metrics路径 含义&#x…...
)
python中的数据类型(价值6980的全能工程师课程笔记)
概述 python数据类型主要分为以下七大类: Numbers(数字) Boolean(布尔) String(字符串) List(列表) Tuple(元组) Dictionary(字典) Set(集合) Python 的七个标准数据类型中: 不可变数据类型(4 个):Number(数字)、Boolean(布尔)、String(字符串)、T…...
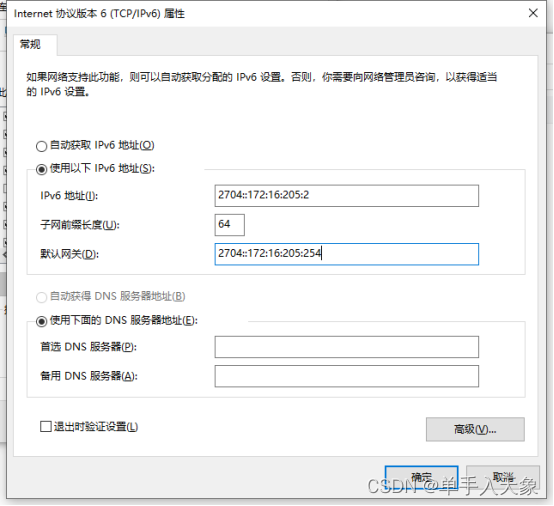
Tomcat 配置IPV6
文章目录一、场景二、tomcat开启ipv6三、ipv6环境配置四、访问总结一、场景 我们在linux下安装一个tomcat,启用ipv6的方式,然后在windows下用浏览器访问这个tomcat 二、tomcat开启ipv6 在server.xml配置文件的里面加上 address”[::]” ,这…...
JavaEE——MyBatis的简单介绍和使用
MyBatis是什么 MyBatis是一个支持普通SQL查询,存储过程以及高级映射的持久层框架,他消除了几乎所有的JDBC代码和参数的手动设置以及对结果集的检索,使用简单的XML或注解进行配置和原始映射,将接口和Java的POJO映射成数据库中的记…...
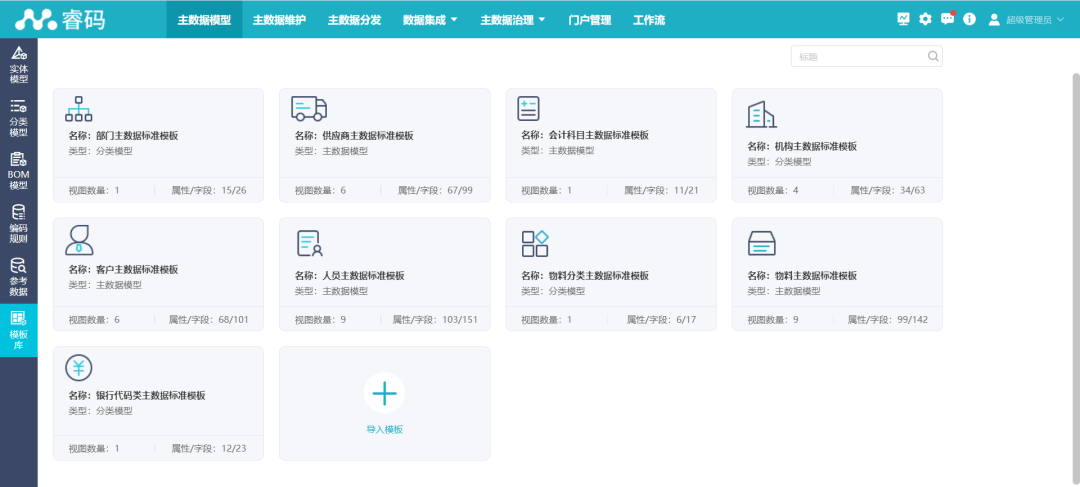
主数据管理平台如何进行模型管理
企业管理主数据,模型管理尤为重要。在对主数据进行建模操作时,既要保证数据通用性、安全性,又要符合企业的业务需求。今天小亿带你认识一下亿信华辰睿码主数据管理平台里的主数据模型管理。 主数据模型分类 一款专业的主数据管理平台&#…...

在 Kubernetes 上运行《我的世界》
最近给小朋友装上了叨叨许久的 Minecraft(我的世界),为了体验安装的是开源启动器 HMCL。其实这游戏我也关注比较久了,不过感觉太耗时间。但被小朋友拉上一起玩,便研究了下自建服务器。GitHub 发现已经有人做好了 Minec…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
