基于MATLAB的MIMO信道估计(附完整代码与分析)
目录
一. 介绍
二. MATLAB代码
三. 运行结果与分析
一. 介绍
本篇将在MATLAB的仿真环境中对比MIMO几种常见的信道估计方法的性能。
有关MIMO的介绍可看转至此篇博客:
MIMO系统模型构建_唠嗑!的博客-CSDN博客
在所有无线通信中,信号通过信道会出现失真,或者会添加各种噪声。正确解码接收到的信号就需要消除信道施加的失真和噪声。为了弄清信道的特性,就需要信道估计。
信道估计有很多不同的方法,但是通用的流程可概括如下:
- 设置一个数学模型,利用信道矩阵搭建起发射信号和接收信号之间的关系;
- 发射已知信号(通常称为参考信号或导频信号)并检测接收到的信号;
- 通过对比发送信号和接收信号,确定信道矩阵中的每个元素。
二. MATLAB代码
一共有四个代码,包含三个函数代码和一个主运行代码。
主运行代码用来产生最后的图像
(1)main.m文件代码
%由于信道数据随机产生,每次运行出的图像可能有略微差异%初始化
close all;
clear all;%%设定仿真参数rng('shuffle'); %产生随机化种子,也可以使用另一函数randn('state',sum(100*clock));%设定蒙特卡洛仿真的数目
nbrOfMonteCarloRealizations = 1000;nbrOfCouplingMatrices = 50; %相关矩阵数目Nt = 8; %发射天线的数量,训练序列的长度
Nr = 4; %接收天线的数量%训练的总功率
totalTrainingPower_dB = 0:1:20; %单位为dB
totalTrainingPower = 10.^(totalTrainingPower_dB/10); %转为线性范围%最优化算法
option = optimset('Display','off','TolFun',1e-7,'TolCon',1e-7,'Algorithm','interior-point');%比较不同的信道估计算法
%实用蒙特卡洛仿真法
average_MSE_MMSE_estimator_optimal = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %最优训练下的MMSE估计法
average_MSE_MMSE_estimator_heuristic = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %启发训练下的MMSE估计法
average_MSE_MVU_estimator = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %最优训练下的MVU估计法
average_MSE_onesided_estimator = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %单边线性估计法
average_MSE_twosided_estimator = zeros(length(totalTrainingPower),nbrOfCouplingMatrices,2); %双边线性估计法%随机信道统计量下的迭代
for statisticsIndex = 1:nbrOfCouplingMatrices%产生Weichselberger模型下的耦合矩阵V%元素均来自卡方分布(自由度为2)V = abs(randn(Nr,Nt)+1i*randn(Nr,Nt)).^2;V = Nt*Nr*V/sum(V(:)); %将矩阵Frobenius范数设为 Nt x Nr.%计算耦合矩阵的协方差矩阵R = diag(V(:));R_T = diag(sum(V,1)); %在Weichselberger模型下,计算发射端的协方差矩阵R_R = diag(sum(V,2)); %在Weichselberger模型下,计算接收端的协方差矩阵%使用MATLAB内置自带的优化算法,计算MMSE估计法下最优的训练功率分配trainingpower_MMSE_optimal = zeros(Nt,length(totalTrainingPower)); %每个训练序列的功率分配向量for k = 1:length(totalTrainingPower) %遍历每个训练序列的功率分配trainingpower_initial = totalTrainingPower(k)*ones(Nt,1)/Nt; %初始设定功率均相等%使用fmincon函数来最优化功率分配%最小化MSE,所有功率均非负trainingpower_MMSE_optimal(:,k) = fmincon(@(q) functionMSEmatrix(R,q,Nr),trainingpower_initial,ones(1,Nt),totalTrainingPower(k),[],[],zeros(Nt,1),totalTrainingPower(k)*ones(Nt,1),[],option);end%计算功率分配[eigenvalues_sorted,permutationorder] = sort(diag(R_T),'descend'); %计算和整理特征值[~,inversePermutation] = sort(permutationorder); %记录特征值的orderq_MMSE_heuristic = zeros(Nt,length(totalTrainingPower));for k = 1:length(totalTrainingPower) %遍历每个训练功率alpha_candidates = (totalTrainingPower(k)+cumsum(1./eigenvalues_sorted(1:Nt,1)))./(1:Nt)'; %计算拉格朗日乘子的不同值optimalIndex = find(alpha_candidates-1./eigenvalues_sorted(1:Nt,1)>0 & alpha_candidates-[1./eigenvalues_sorted(2:end,1); Inf]<0); %找到拉格朗日乘子的αq_MMSE_heuristic(:,k) = max([alpha_candidates(optimalIndex)-1./eigenvalues_sorted(1:Nt,1) zeros(Nt,1)],[],2); %使用最优的α计算功率分配endq_MMSE_heuristic = q_MMSE_heuristic(inversePermutation,:); %通过重新整理特征值来确定最终的功率分配%计算均匀功率分配q_uniform = (ones(Nt,1)/Nt)*totalTrainingPower;%蒙特卡洛仿真初始化vecH_realizations = sqrtm(R)*( randn(Nt*Nr,nbrOfMonteCarloRealizations)+1i*randn(Nt*Nr,nbrOfMonteCarloRealizations) ) / sqrt(2); %以向量的形式产生信道 vecN_realizations = ( randn(Nt*Nr,nbrOfMonteCarloRealizations)+1i*randn(Nt*Nr,nbrOfMonteCarloRealizations) ) / sqrt(2); %以向量的形式产生噪声%对于每种估计方法计算MSE和训练功率for k = 1:length(totalTrainingPower)%MMSE估计法:最优训练功率分配P_tilde = kron(diag(sqrt(trainingpower_MMSE_optimal(:,k))),eye(Nr)); %计算有效功率矩阵average_MSE_MMSE_estimator_optimal(k,statisticsIndex,1) = trace(R - (R*P_tilde'/(P_tilde*R*P_tilde' + eye(length(R))))*P_tilde*R); %计算MSEH_hat = (R*P_tilde'/(P_tilde*R*P_tilde'+eye(length(R)))) * (P_tilde*vecH_realizations+vecN_realizations); %使用蒙特卡洛仿真来计算该估计average_MSE_MMSE_estimator_optimal(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSE%MMSE估计法:启发式训练功率分配MMSE P_tilde = kron(diag(sqrt(q_MMSE_heuristic(:,k))),eye(Nr)); %计算有效训练矩阵average_MSE_MMSE_estimator_heuristic(k,statisticsIndex,1) = trace(R - (R*P_tilde'/(P_tilde*R*P_tilde' + eye(length(R))))*P_tilde*R); %计算MSEH_hat = (R*P_tilde'/(P_tilde*R*P_tilde'+eye(length(R)))) * (P_tilde*vecH_realizations + vecN_realizations); %使用蒙特卡洛仿真来计算该估计average_MSE_MMSE_estimator_heuristic(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSE%MVY估计法: 最优均匀训练功率分配P_training = diag(sqrt(q_uniform(:,k))); %均匀功率分配P_tilde = kron(transpose(P_training),eye(Nr)); %计算有效训练矩阵P_tilde_pseudoInverse = kron((P_training'/(P_training*P_training'))',eye(Nr)); %计算有效训练矩阵的伪逆average_MSE_MVU_estimator(k,statisticsIndex,1) = Nt^2*Nr/totalTrainingPower(k); %计算MSEH_hat = P_tilde_pseudoInverse'*(P_tilde*vecH_realizations + vecN_realizations); %使用蒙特卡洛仿真来计算该估计average_MSE_MVU_estimator(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSE%One-sided linear 估计法: 最优训练功率分配又被称为 "LMMSE 估计法" P_training = diag(sqrt(q_MMSE_heuristic(:,k))); %使用最优功率分配来计算训练矩阵 P_tilde = kron(P_training,eye(Nr)); %计算有效训练矩阵average_MSE_onesided_estimator(k,statisticsIndex,1) = trace(inv(inv(R_T)+P_training*P_training'/Nr)); %计算MSEAo = (P_training'*R_T*P_training + Nr*eye(Nt))\P_training'*R_T; %计算one-sided linear估计法中的矩阵A0 H_hat = kron(transpose(Ao),eye(Nr))*(P_tilde*vecH_realizations + vecN_realizations); %使用蒙特卡洛仿真来计算该估计average_MSE_onesided_estimator(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MS%Two-sided linear 估计法: 最优训练功率分配P_training = diag(sqrt(q_uniform(:,k))); %计算训练矩阵,均匀功率分配P_tilde = kron(P_training,eye(Nr)); %计算有效训练矩阵R_calE = sum(1./q_uniform(:,k))*eye(Nr); %计算协方差矩阵average_MSE_twosided_estimator(k,statisticsIndex,1) = trace(R_R-(R_R/(R_R+R_calE))*R_R); %计算MSEC1 = inv(P_training); %计算矩阵C1C2bar = R_R/(R_R+R_calE); %计算C2bar矩阵H_hat = kron(transpose(C1),C2bar)*(P_tilde*vecH_realizations + vecN_realizations);average_MSE_twosided_estimator(k,statisticsIndex,2) = mean( sum(abs(vecH_realizations - H_hat).^2,1) ); %使用蒙特卡洛仿真来计算MSendend%挑选训练功率的子集
subset = linspace(1,length(totalTrainingPower_dB),5);normalizationFactor = Nt*Nr; %设定MSE标准化因子为trace(R), 标准化MSE为从0到1.%使用理论MSE公式画图
figure(1); hold on; box on;plot(totalTrainingPower_dB,mean(average_MSE_MVU_estimator(:,:,1),2)/normalizationFactor,'b:','LineWidth',2);plot(totalTrainingPower_dB,mean(average_MSE_twosided_estimator(:,:,1),2)/normalizationFactor,'k-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_onesided_estimator(:,:,1),2)/normalizationFactor,'r-','LineWidth',1);plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_heuristic(subset(1),:,1),2)/normalizationFactor,'b+-.','LineWidth',1);
plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_optimal(subset(1),:,1),2)/normalizationFactor,'ko-','LineWidth',1);legend('MVU, optimal','Two-sided linear, optimal','One-sided linear, optimal','MMSE, heuristic','MMSE, optimal','Location','SouthWest')plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_heuristic(:,:,1),2)/normalizationFactor,'b-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_optimal(:,:,1),2)/normalizationFactor,'k-','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_heuristic(subset,:,1),2)/normalizationFactor,'b+','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_optimal(subset,:,1),2)/normalizationFactor,'ko','LineWidth',1);set(gca,'YScale','Log'); %纵轴为log范围
xlabel('Total Training Power (dB)');
ylabel('Average Normalized MSE');
axis([0 totalTrainingPower_dB(end) 0.05 1]);title('Results based on theoretical formulas');%使用蒙特卡洛仿真画理论运算图
figure(2); hold on; box on;plot(totalTrainingPower_dB,mean(average_MSE_MVU_estimator(:,:,2),2)/normalizationFactor,'b:','LineWidth',2);
plot(totalTrainingPower_dB,mean(average_MSE_twosided_estimator(:,:,2),2)/normalizationFactor,'k-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_onesided_estimator(:,:,2),2)/normalizationFactor,'r-','LineWidth',1);
plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_heuristic(subset(1),:,2),2)/normalizationFactor,'b+-.','LineWidth',1);
plot(totalTrainingPower_dB(subset(1)),mean(average_MSE_MMSE_estimator_optimal(subset(1),:,2),2)/normalizationFactor,'ko-','LineWidth',1);legend('MVU, optimal','Two-sided linear, optimal','One-sided linear, optimal','MMSE, heuristic','MMSE, optimal','Location','SouthWest')plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_heuristic(:,:,2),2)/normalizationFactor,'b-.','LineWidth',1);
plot(totalTrainingPower_dB,mean(average_MSE_MMSE_estimator_optimal(:,:,2),2)/normalizationFactor,'k-','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_heuristic(subset,:,2),2)/normalizationFactor,'b+','LineWidth',1);
plot(totalTrainingPower_dB(subset),mean(average_MSE_MMSE_estimator_optimal(subset,:,2),2)/normalizationFactor,'ko','LineWidth',1);set(gca,'YScale','Log'); %纵轴为log范围
xlabel('Total Training Power (dB)');
ylabel('Average Normalized MSE');
axis([0 totalTrainingPower_dB(end) 0.05 1]);title('Results based on Monte-Carlo simulations');包含每行具体代码的解释
(2)三个函数文件
function [deviation,powerAllocation]=functionLagrangeMultiplier(eigenvaluesTransmitter,totalPower,k,alpha)
%Compute the MSE for estimation of the squared Frobenius norm of the
%channel matrix for a given training power allocation.
%INPUT:
%eigenvaluesTransmitter = Vector with the active eigenvalues at the
% transmitter side
%totalPower = Total power of the training sequence
%k = Vector with k parameter values
%alpha = Langrange multiplier value
%
%OUTPUT:
%deviation = Difference between available power and used power
%powerAllocation = Training power allocation
%Compute power allocation
powerAllocation = sqrt(8*(1./alpha(:))*eigenvaluesTransmitter'/3).*cos(repmat((-1).^k*pi/3,[length(alpha) 1])-atan(sqrt(8*(1./alpha(:))*(eigenvaluesTransmitter.^3)'/27-1))/3)-repmat(1./eigenvaluesTransmitter',[length(alpha) 1]);%Deviation between total available power and the power that is used
deviation = abs(totalPower-sum(powerAllocation,2));function MSE = functionMSEmatrix(R_diag,q_powerallocation,B)
%Compute the MSE for estimation of the channel matrix for a given training
%power allocation.
%INPUT:
%R_diag = Nt Nr x Nt Nr diagonal covariance matrix
%q_powerallocation = Nt x 1 vector with training power allocation
%B = Length of the training sequence.
%
%OUTPUT:
%MSE = Mean Squared Error for estimation of the channel matrixP_tilde = kron(diag(sqrt(q_powerallocation)),eye(B));MSE = trace(R_diag - R_diag*(P_tilde'/(P_tilde*R_diag*P_tilde'+eye(length(R_diag))))*P_tilde*R_diag);function MSE = functionMSEnorm(eigenvaluesTransmitter,eigenvaluesReceiver,powerAllocation)
%Compute the MSE for estimation of the squared Frobenius norm of the
%channel matrix for a given training power allocation.
%INPUT:
%eigenvaluesTransmitter = Nt x 1 vector with eigenvalues at the
% transmitter side
%eigenvaluesReceiver = Nr x 1 vector with eigenvalues at the
% receiver side
%powerAllocation = Nt x 1 vector with training power allocation
%
%OUTPUT:
%MSE = Mean Squared Error for estimation of the squared normMSE = sum(sum(((eigenvaluesTransmitter*eigenvaluesReceiver').^2 + 2*(powerAllocation.*eigenvaluesTransmitter.^3)*(eigenvaluesReceiver').^3)./(1+(powerAllocation.*eigenvaluesTransmitter)*eigenvaluesReceiver').^2));
注意:
- 此MIMO发射天线为8,接收天线为4;
- 三个函数文件的命名需要与函数保持一致;
- 先运行函数文件,再运行main主文件;
- 函数文件出现变量数报错是正常现象;
- 运行出来有两个图,选择任意一个图即可。
三. 运行结果与分析
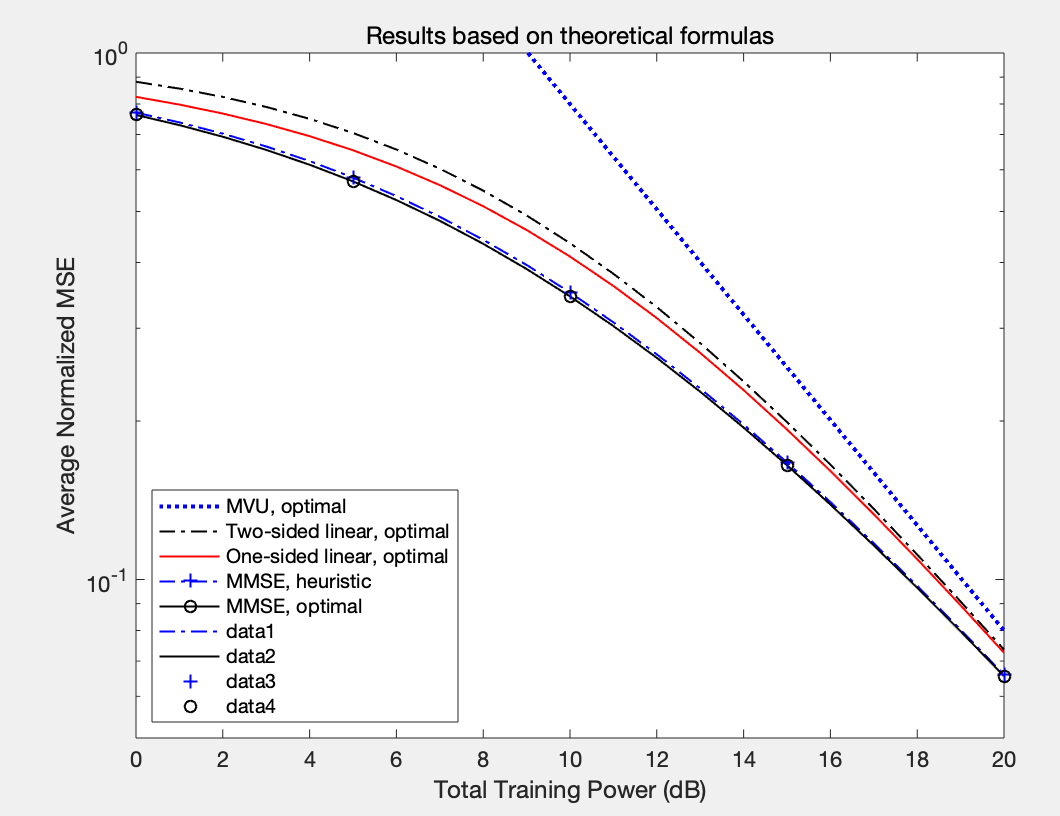
分析:
- 横向看,当训练功率增加时,均方误差(MSE)在减小,符合信道估计的基本逻辑;
- 纵向对比,MMSE(optimal)》MMSE(heuristic)》one-sided linear》two-side linear>MVU
》代表左边优于右边,每一个位置代表一种信道估计方法
相关文章:

基于MATLAB的MIMO信道估计(附完整代码与分析)
目录 一. 介绍 二. MATLAB代码 三. 运行结果与分析 一. 介绍 本篇将在MATLAB的仿真环境中对比MIMO几种常见的信道估计方法的性能。 有关MIMO的介绍可看转至此篇博客: MIMO系统模型构建_唠嗑!的博客-CSDN博客 在所有无线通信中,信号通过…...

Python代码游戏————星球大战
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放,树高千尺,落叶归根人生不易,人间真情 目录 一.Python介绍 二.游戏效果呈现 三.主代码 四....

java向Word模板中替换书签数据,插入图片,插入复选框,插入Word中表格的行数据,删除表格行数据
java向Word模板中替换书签数据,插入图片,插入复选框,插入Word中表格的行数据,删除表格行数据 使用插件:spire.doc 创建工具类,上代码: import com.spire.doc.Document; import com.spire.doc.…...
)
Java基础知识快速盘点(二)
一,类型转换 隐式转换 将一个类型转换为另一个类型时,系统默认转换常量优化机制算术运算时类型的隐式转换(byte,short在算术运算时都会转换为int)char类型在进行运算时会根据其编码值进行运算 显式转换 二࿰…...
企业降本增效的催化剂:敏捷迭代
伴随着开源技术的大爆发,新一代的软件技术如雨后春笋般层出不穷。每家企业在硬件及软件开发上都有许多开源技术可选,目的还是在于提高效率,降低开发成本。 本篇文章,带大家了解下促进企业降本增效的重要理念:敏捷迭代…...
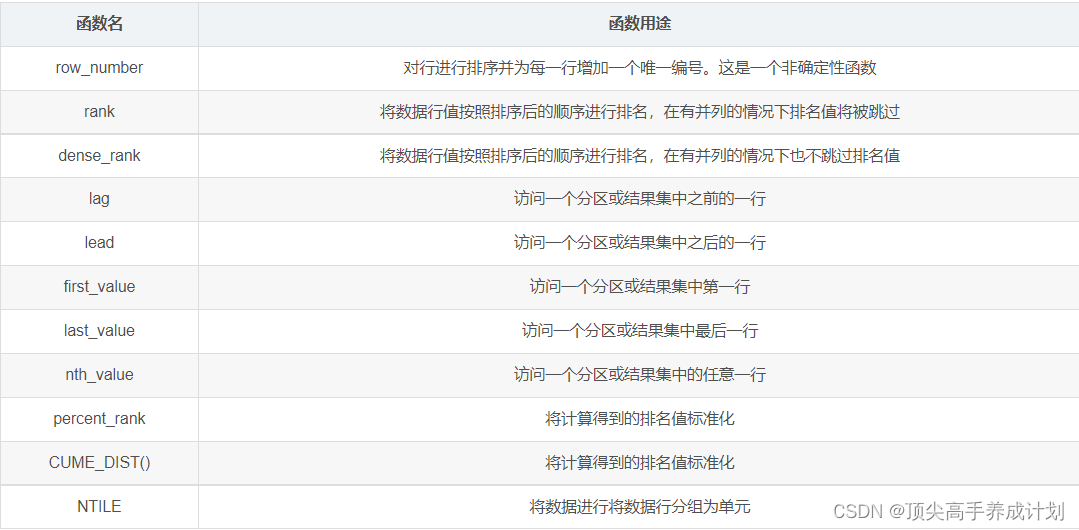
MySQL入门篇-MySQL高级窗口函数简介
备注:测试数据库版本为MySQL 8.0 这个blog我们来聊聊MySQL高级窗口函数 窗口函数在复杂查询以及数据仓库中应用得比较频繁 与sql打交道比较多的技术人员都需要掌握 如需要scott用户下建表及录入数据语句,可参考:scott建表及录入数据sql脚本 分析函数有3个基本组成…...
?)
什么是 API(应用程序接口)?
API(应用程序接口)是一种软件中介,它允许两个不相关的应用程序相互通信。它就像一座桥梁,从一个程序接收请求或消息,然后将其传递给另一个程序,翻译消息并根据 API 的程序设计执行协议。API 几乎存在于我们…...
如何在外网访问内网的 Nginx 服务?
计算机业内人士对Nginx 并不陌生,它是一款轻量级的 Web 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器,除了nginx外,类似的apache、tomcat、IIS这几种都是主流的中间件。 Nginx 是在 BSD-like 协议下发行的&…...

vue2中defineProperty和vue3中proxy区别
区别一:defineProperty 是对属性劫持,proxy 是对代理对象 下面我们针对一个对象使用不同的方式进行监听,看写法上有什么不同。 // 原始对象 const data {name: Jane,age: 21 }defineProperty defineProperty 只能劫持对象的某一个属性&…...

将bean注入Spring容器的五种方式
前言 我们在项目开发中都用到Spring,知道对象是交由Spring去管理。那么将一个对象加入到Spring容器中,有几种方法呢,我们来总结一下。 ComponentScan Component ComponentScan可以放在启动类上,指定要扫描的包路径;…...

C生万物 | 常量指针和指针常量的感性理解
文章目录📚引言✒常量指针🔍介绍与分析📰小结与记忆口诀✒指针常量🔍介绍与分析📰小结与记忆口诀👉一份凉皮所引发的故事👈总结与提炼📚引言 本文我们来说说大家很困惑的两个东西&am…...

python 打包工具 pyinstaller和Nuitka区别
1.1 使用需求 这次也是由于项目需要,要将python的代码转成exe的程序,在找了许久后,发现了2个都能对python项目打包的工具——pyintaller和nuitka。 这2个工具同时都能满足项目的需要: 隐藏源码。这里的pyinstaller是通过设置key来…...
Python解题 - CSDN周赛第28期
上一期周赛问哥因为在路上,无法参加,但还是抽空登上来看了一下题目。4道题都挺简单的,有点遗憾未能参加。不过即使参加了,手速也未必能挤进前十。 本期也是一样,感觉新增的题目都偏数学类,基本用不到所谓的…...

DNS记录类型有哪些,分别代表什么含义?
DNS解析将域名指向IP地址,是互联网中的一项重要服务。而由于业务场景不同,在设置DNS解析时,需要选择不同的记录类型。网站管理人员需要准确了解每一种DNS记录类型所代表的含义和用途,才能满足不同场景的解析需求。本文中科三方简单…...

ICLR 2022—你不应该错过的 10 篇论文(上)
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 ICLR 2023已经放榜,但是今天我们先来回顾一下去年的ICLR 2022! ICLR 2022将于2022年 4 月 25 日星期一至 4 月 29 日星期五在线举行(连续第三年!…...

HydroD 实用教程(三)环境数据
目 录一、前言二、Location三、Wind Profile四、Directions五、Water5.1 Wave Spectrums5.2 Current Profile5.3 Frequency Set5.4 Phase Set5.5 Wave Height5.6 Regular Wave Set六、参考文献一、前言 SESAM (Super Element Structure Analysis Module)…...

第四章 统计机器学习
机器学习:从数据中学习知识; 原始数据中提取特征;学习映射函数f;通过映射函数f将原始数据映射到语义空间,即寻找数据和任务目标之间的关系; 机器学习: 监督学习:数据有标签&#x…...
Redis第一讲
目录 一、Redis01 1.1 NoSql 1.1.1 NoSql介绍 1.1.2 NoSql起源 1.1.3 NoSql的使用 1.2 常见NoSql数据库介绍 1.3 Redis简介 1.3.1 Redis介绍 1.3.2 Redis数据结构的多样性 1.3.3 Redis应用场景 1.4 Redis安装、配置以及使用 1.4.1 Redis安装的两种方式 1.4.2 Redi…...

Java面试题-消息队列
消息队列 1. 消息队列的使用场景 六字箴言:削峰、异步、解耦 削峰:接口请求在某个时间段内会出现峰值,服务器在达到峰值的情况下会奔溃;通过消息队列将请求进行分流、限流,确保服务器在正常环境下处理请求。异步&am…...

基于离散时间频率增益传感器的P级至M级PMU模型的实现(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

PostgreSQL 对 IPv6 的支持情况
PostgreSQL 对 IPv6 的支持情况 PostgreSQL 全面支持 IPv6 网络协议,包括连接、存储和操作 IPv6 地址。以下是详细说明: 一、网络连接支持 1. 监听 IPv6 连接 在 postgresql.conf 中配置: listen_addresses 0.0.0.0,:: # 监听所有IPv4…...

如何使用CodeRider插件在IDEA中生成代码
一、环境搭建与插件安装 1.1 环境准备 名称要求说明操作系统Windows 11JetBrains IDEIntelliJ IDEA 2025.1.1.1 (Community Edition)硬件配置推荐16GB内存50GB磁盘空间 1.2 插件安装流程 步骤1:市场安装 打开IDEA,进入File → Settings → Plugins搜…...
