图的基本概念
1、图的概念
G=(V,E)
图G由节点集合V=V(G)和边集合E=E(G)组成,其中V为非空有限集合。
集合V中的节点(node)用红色标出,通过集合E中黑色的边(edge)连接。

G的边:E中的每个顶点对(u,v)称为G的边
边的端点:用e表示集合E中的一个顶点对e=(u, v),称u,v为边e的端点
邻接顶点:称u和v是邻接的顶点
关联:一条边的端点称为与这条边关联
邻接的边:若两条不同的边与一个公共的端点关联,称这两条边是邻接的
多重边:若联结两个顶点有不止一条边,这些边称为多重边
环:顶点重合为一点的边称为环
简单图 :没有环也没有多重边的图称为简单图
有限图:一个图如果它的顶点集合与边集合都有限,称为有限图
空图:没有边的图称为空图
标定图:给每一个定点和每一条边指定一个符号,则称这样的图为标定图
完全图:完全图是一个简单的无向图,其中每对不同的顶点之间都有一条边相连
二分图:若图G的顶点集合能分为两个子集V和U,使每一条边有一个端点在V中另一个端点在U中,则称此图为二分图(或二部图)记作G(V,U,E)
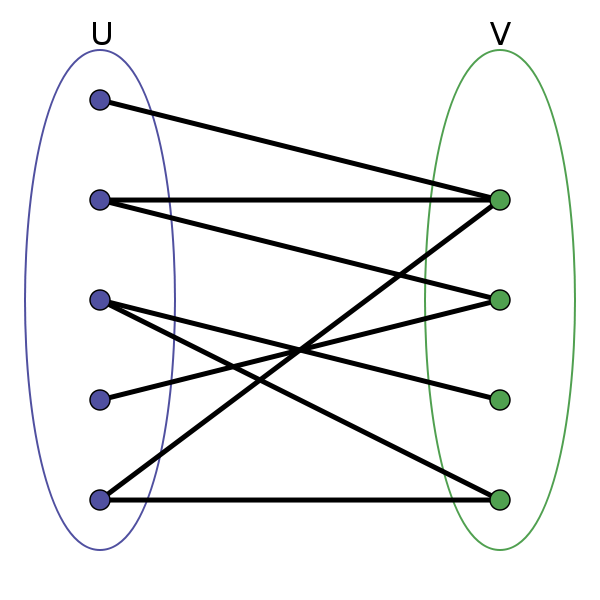
完全二分图 :若V的每个顶点与U的每个顶点都关联,称为完全二分图
补图:一个图G的补图Gˉ\bar{G}Gˉ也是以V(G)为顶点集的一个图,但是两个顶点在Gˉ\bar{G}Gˉ中邻接当且仅当它们在G中不邻接。下图b为a的补图。是完全图去除G的边集后得到的图。
子图:所有顶点和边都属于图G的图称为G的子图
生成子图:含有G的所有顶点的子图称为G的生成子图
导出子图:设图G = (V, E),令S⊂V,使得S是G的任意顶点子集。则G的导出子图G(S)中,其顶点集为S,边集为G的边集E中两个顶点均属于S的边的集合。
2、顶点的度
图G中和一个顶点viv_{i}vi关联的边的数目叫做顶点viv_{i}vi的度,记作deg(vi)deg (v_{i})deg(vi)
定理 1:设G是一个(p, q)图,那么G的各个顶点度的和是边数的二倍:
∑vi∈V(G)deg(vi)=2q\sum_{v_{i}\in V(G) }^{} deg (v_{i}) = 2q vi∈V(G)∑deg(vi)=2q
推论 1:在任何一个图G中,度为奇数的顶点的数目是偶数。
在一个(p, q)图中,对每个顶点v均有0≤deg(v)≤p−10\le deg (v) \le p-10≤deg(v)≤p−1
孤立点:若 deg (v) = 0,则称v是孤立点
悬挂点:若 deg (v) = 1,称v是一个悬挂点
正则的图:若图G的所有顶点的度均相等,则称G为正则的
r度正则的图:顶点的度均为r的正则图称为r度正则图
出度:指出节点的边数量
入度:指向节点的边数量
定理 2:所有节点入度和等于所有节点出度和
定理3 :n个节点的无向完全图 边数为n(n-1)/2
3、图的连通性
通路
通路:给定图G=(V, E)中的节点和边相继交错出现的序列:
Γ=v0e1v1e2v2...ekvk\Gamma = v_{0} e_{1} v_{1} e_{2} v_{2} ... e_{k} v_{k}Γ=v0e1v1e2v2...ekvk称Γ\GammaΓ为节点v0v_{0}v0到节点v0v_{0}v0的通路。(其中边eie_{i}ei的两端点是vi−1v_{i-1}vi−1和viv_{i}vi,有向图时vi−1v_{i-1}vi−1与viv_{i}vi分别是eie_{i}ei的始点和终点)
通路的端点:v0v_{0}v0和vkv_{k}vk分别称为此通路的始点和终点,统称为通路的端点。
通路的长度: 通路中边的数目称为此通路的长度
回路:当v0v_{0}v0 = vkv_{k}vk时,此通路称为回路
简单通路:若通路中的所有边互不相同,称此通路为简单通路(也叫做轨迹trail)
简单回路:若回路中的所有边互不相同,称此回路为简单回路
基本通路:通路中所有节点互不相同,所有边也互不相同的通路(也叫做路径path)
基本回路:回路中除v0v_{0}v0 = vkv_{k}vk以外所有节点互不相同,所有边也互不相同的回路
通路长度:一条通路上所有边的权的和称为该通路的长度
图的直径:是指连接任意两个节点的所有最短通路中最长的通路长度
连通图
连通:在无向图 G 中,若从顶点i到顶点j有路径相连(当然从j到i也一定有路径)则称i和j是连通的;如果 G 是有向图,那么连接i和j的路径中所有的边都必须同向。
连通图:如果图中任意两点都是连通的,那么图被称作连通图。
强连通图:如果有向图图中任意两点都是连通的,并且双向都有路径,那么这个有向图图被称作强连通图
连通分量:无向图G的极大连通子图称为G的连通分量( Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。
环路:回路与回路的边的不重并,称为环路
定理3.1:闭链是环路
定理3.2:环路中每个顶点的度均为偶数
定理:连通(p, q)图G关于生成树T的基本回路组做成G的一个基底,且环路空间的维数是q-p+1。由于基本回路组不是唯一的,环路空间的基底也不是唯一的
推论:连通的(p, q)图的环路空间中元素的个数是2q−p+12^{q-p+1}2q−p+1(包括空图)
4、图的运算
设G1G_{1}G1和G2G_{2}G2是没有孤立点的图
G1G_{1}G1和G2G_{2}G2的 并:由G1G_{1}G1和G2G_{2}G2中所有边组成图,记作G1∪G2G_{1} \cup G_{2}G1∪G2
G1G_{1}G1和G2G_{2}G2的 交:由G1G_{1}G1和G2G_{2}G2的公共边组成的图,记作G1∩G2G_{1} \cap G_{2}G1∩G2
G1G_{1}G1与G2G_{2}G2的 差:在G1G_{1}G1中去掉G2G_{2}G2的边所得到的图,记作G1−G2G_{1} - G_{2}G1−G2
G1G_{1}G1和G2G_{2}G2的 环和:在G1G_{1}G1和G2G_{2}G2的并中去掉G1G_{1}G1和G2G_{2}G2的交得到的图,记作 G1⊕G2G_{1}\oplus G_{2}G1⊕G2
5、树的概念
树:一个连通的无回路的图称为树。
定理5.1:在树中任意两个顶点均由唯一的通路联结
定理5.2:设T是一个(p, q)图,若T是一棵树,则q = p-1
定理5.3:设T是一棵树,若在T的任何两个不临近的顶点联一条边e,则T+e恰有一条回路
定理5.4:如果图G的任意两个顶点由唯一的通路联结,那么G是一棵树
定理5.5:设G是一个(p, q)图,如果G是连通的,且q=p-1,则G是一棵树
定理5.6:设G是一个(p, q)图,如果G无回路且q=p-1,则G是一棵树
割边(桥):去掉图的一条边后,剩下的图的支比原图多(暨图不再连通)
割点:在无向图中删除某顶点后图不再连通,则这个顶点就是这个图的割点
不可分图:连通的没有割点的图称为不可分图
定理5.7:当且仅当G的一条边e不包含在G的回路中时,e才是割边
定理5.8:当且仅当某连通图的每条边均为割边时,该连通图才是一棵树
定理5.9:当且仅当在G中存在与v不同的两个顶点u和w使v在每一条(u, w)通路上v才是割点
定理5.10:设v是树T的一个顶点,则当且仅当degv>1时,v才是割点
定理5.11:每个连通图G至少有两个顶点不是割点
推理5.1:每棵树至少有两个度为1的顶点,且树中最长通路的起点和终点的度均为1
定理5.12:不可分图的任一边至少在一个回路中
6、图的矩阵表示
(1)关联矩阵
完全关联矩阵:
设G是一个(p,q)图,令aij={1,若边j与顶点i关联0,否则a_{ij} = \left\{\begin{matrix} 1,& 若边j与顶点i关联\\ 0,& 否则 \end{matrix}\right.aij={1,0,若边j与顶点i关联否则
则称由元素aija_{ij}aij(i=1,…,p,j=1,…,q)构成的p×\times×q矩阵为图G的完全关联矩阵
定理6.1:设G是连通的(p, q)图,那么G的完全关联矩阵的秩是p-1
推论6.1:完全关联矩阵的秩等于它所表示的图的秩
定理6.2:G为连通的(p, q)图,当且仅当G的完全关联矩阵的秩为p-1
大子阵:p×\times×q矩阵的阶为min{p, q}的方阵,称为p×\times×q矩阵的一个大子阵
大行列式:大子阵定义的行列式称为大行列式
定理6.3:设G是一个连通的(p, q)图。G的关联矩阵的一个大子阵是非奇异的当且仅当与这个大子阵的列相对应的边组成G的一颗生成树
(2)回路矩阵
完全回路矩阵:
设G是一个(p,q)图,令bij={1,若边j在环路i中0,否则b_{ij} = \left\{\begin{matrix} 1,& 若边j在环路i中\\ 0,& 否则 \end{matrix}\right.bij={1,0,若边j在环路i中否则
则称由元素bijb_{ij}bij(i=1,…,2q−p+12^{q-p+1}2q−p+1,j=1,…,q)构成的2q−p+12^{q-p+1}2q−p+1×\times×q矩阵为图G的完全回路矩阵
定理6.4:连通的(p, q)图G的完全回路矩阵的秩等于q-p+1
定理6.5:连通的(p, q)图G的关联矩阵A和完全回路矩阵B满足ABTAB^{T}ABT = 0,BATBA^{T}BAT = 0
推论6.2:设B是图G的回路矩阵,则ABTAB^{T}ABT = 0,BATBA^{T}BAT = 0
(3)割集矩阵
完全割集矩阵:
设G是一个(p,q)图,令qij={1,若边j在断集i中0,否则q_{ij} = \left\{\begin{matrix} 1,& 若边j在断集i中\\ 0,& 否则 \end{matrix}\right.qij={1,0,若边j在断集i中否则
则称由元素qijq_{ij}qij(i=1,…,2p−12^{p-1}2p−1-1,j=1,…,q)构成的(2p−1−1)(2^{p-1}-1)(2p−1−1)×\times×q矩阵为图G的完全回路矩阵
(4)邻接矩阵
邻接矩阵:
一个图G=(V, X)由V中每两个点间的邻接关系唯一决定,这种关系可以用一个矩阵来表示。设V={v1,...vpv_{1},...v_{p}v1,...vp},p阶方阵A(G) =(aija_{ij}aij)称为G的邻接矩阵:
若 aij={1,vi邻接于vj0,vi不邻接于vj或i=ja_{ij} = \left\{\begin{matrix} 1,& v_{i}邻接于v_{j}\\ 0,& v_{i}不邻接于v_{j}或i=j \end{matrix}\right.aij={1,0,vi邻接于vjvi不邻接于vj或i=j
(5)拉普拉斯矩阵
给定一个有n个顶点的图G,它的拉普拉斯矩阵L=(li,j)n,n(l_{i,j})_{n,n}(li,j)n,n定义为:
L=D−AL=D-AL=D−A其中D为图的度矩阵,A为图的邻接矩阵。
7、图的存储
(1)邻接矩阵
图的邻接矩阵表示法(Adjacency Matrix):也称作数组表示法。
采用两个数组来表示图: 一个是用于存储顶点信息的一维数组;另一个是用于存储图中顶点之间关联关系的二维数组,这个关联关系数组被称为邻接矩阵。
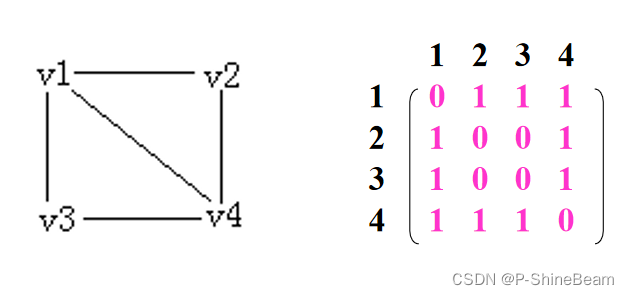
- 在图中各顶点的序号确定后,图的邻接矩阵是唯一确定的
- 邻接矩阵可采用压缩存储
- 适于进行边或弧的删除和插入操作
- 不易于进行顶点的插入删除操作
- 对于稀疏图会造成存储空间的浪费
(2)邻接表
邻接表表示法(Adjacency List):实际上是图的一种链式存储结构。
基本思想是只存有关联的信息,对于图中存在的边信息则存储,而不相邻接的顶点则不保留信息。在邻接表中,对图中的每个顶点建立一个带头结点的边链表。每个边链表的头结点又构成一个表头结点表。一个n个顶点的图的邻接表表示由表头结点表与边链表两部分构成:
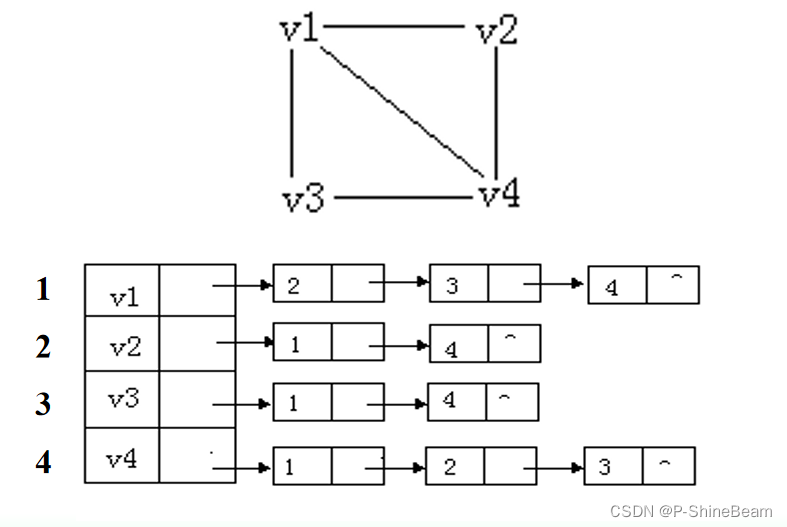
特点:
- 图的邻接表表示不唯一的,它与边结点的次序有关
- 对于顶点多边少的图采用邻接表存储节省空间
- 容易找到任一顶点的第一个邻接点和下一个邻接点
- 无向图的邻接表中第i个顶点的度为第i个链表中结点的个数
- 有向图的邻接表中第i个链表的结点的个数是第i个顶点的出度;而第i个顶点的入度需遍历整个链表,采用逆邻接表,建立一个以vi顶点为头的弧的表
- 无向图的边数等于邻接表中边结点数的一半,有向图的弧数等于邻接表中边结点数
(3)十字链表
邻接表表示有向图时,每个结点对应的边表表示结点的出度信息,无法表示入度信息。
可以采用逆邻接矩阵的方式表示出度信息但不能表示入度信息。因此,考虑将邻接表与逆邻接表结合同时表示有向图的出入度信息,得到十字链表的表示方式
(4)邻接多重表
邻接表表示无向图时边链表会存在大量边信息的冗余,因为邻接表中每条边用两个结点表示的。为了降低冗余,邻接多重表的边链表改用一个边结点表示边来降低冗余。
8、图的常见算法
(1) 寻路和图搜索算法
-
寻路算法:寻找两个节点之间的最短路径。最短路径计算的是一对节点之间的最短的加权(如果图有加权的话)路径。常用算法有:Dijkstra 算法等
-
搜索算法:根据图的相邻情况或深度来探索图,这可用于信息检索;常用算法有:宽度优先搜索(BFS)、深度优先搜索(DFS)
(2) 社群检测
- 社群检测:根据给定的质量指标将节点划分为多个分组,常用算法有Girvan Newman 算法、Louvain 方法、分层聚类算法等
(3) 中心度算法
中心度(Centrality)衡量的是节点的重要程度。但这并非一个明晰的定义。常用算法有PageRank 算法等
参考资料
1、图论【王朝瑞编著】
2、图论与图学习
3、图论基础
相关文章:

图的基本概念
1、图的概念 G(V,E) 图G由节点集合VV(G)和边集合EE(G)组成,其中V为非空有限集合。 集合V中的节点(node)用红色标出,通过集合E中黑色的边(edge)连接。 G的边:E中的每个顶点对&#x…...
MySQL必会四大函数-窗口函数
在了解窗口函数之前,我们必须了解聚合函数。常见的聚合函数,包括 AVG、COUNT、MAX、MIN、SUM 以及 GROUP_CONCAT,常和GROUP BY 函数一起使用。聚合函数的作用就是对一组数据行进行汇总计算,并且返回单个分析结果。 窗口函数和聚合…...

各CCF期刊点评网站/学术论坛的信息汇总及个人评价
CCF中文期刊投稿选择之篇章一:各CCF期刊点评网站/学术论坛的信息汇总及个人评价中文科技期刊A类(EI检索)中文期刊投稿点评网站整理1.小木虫学术论坛2. Letpub3. Justscience4. 发表记5. 会伴(Conference Partner)6. ijouranl7. 掌桥科研这是以…...

深度解析 JavaScript 严格模式:利弊长远的考量
前言 ECMAScript 5首次引入严格模式的概念。严格模式用于选择以更严格的条件检查JavaScript代码错误,可以应用到全局,也可以应用到函数内部。 严格模式的好处是可以提早发现错误,因此可以捕获某些 ECMAScript 问题导致的编程错误。 理解严格…...

Vue.js 循环语句
Vue.js 循环语句 在Vue开发中,for循环是我们最常遇见的场景之一,我们知道常见的遍历方式有for循环,for of、forEach、for in.虽然在开发过程中,这几种方式基本上可以满足我们大多数的场景,但是你真的知道他们之间的区…...
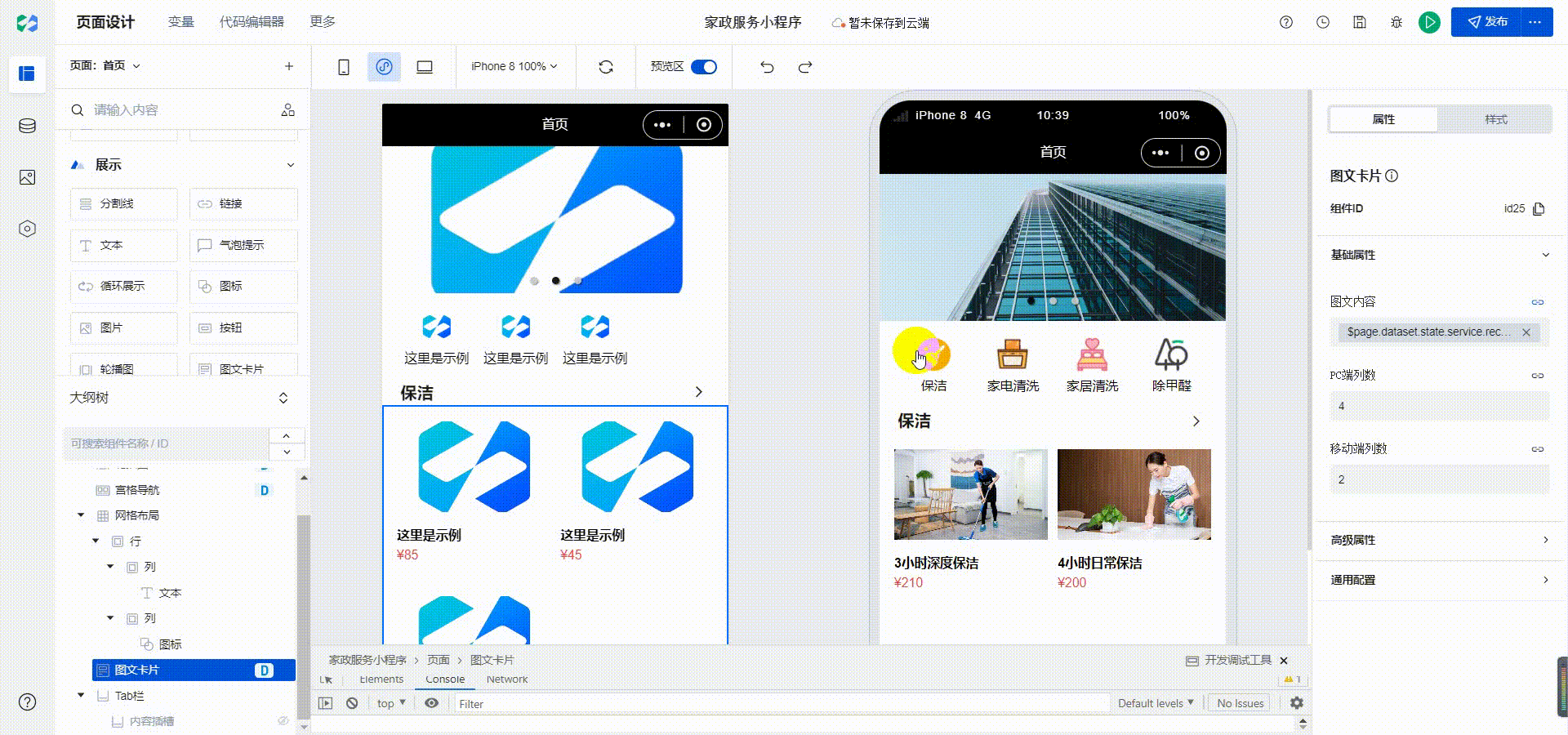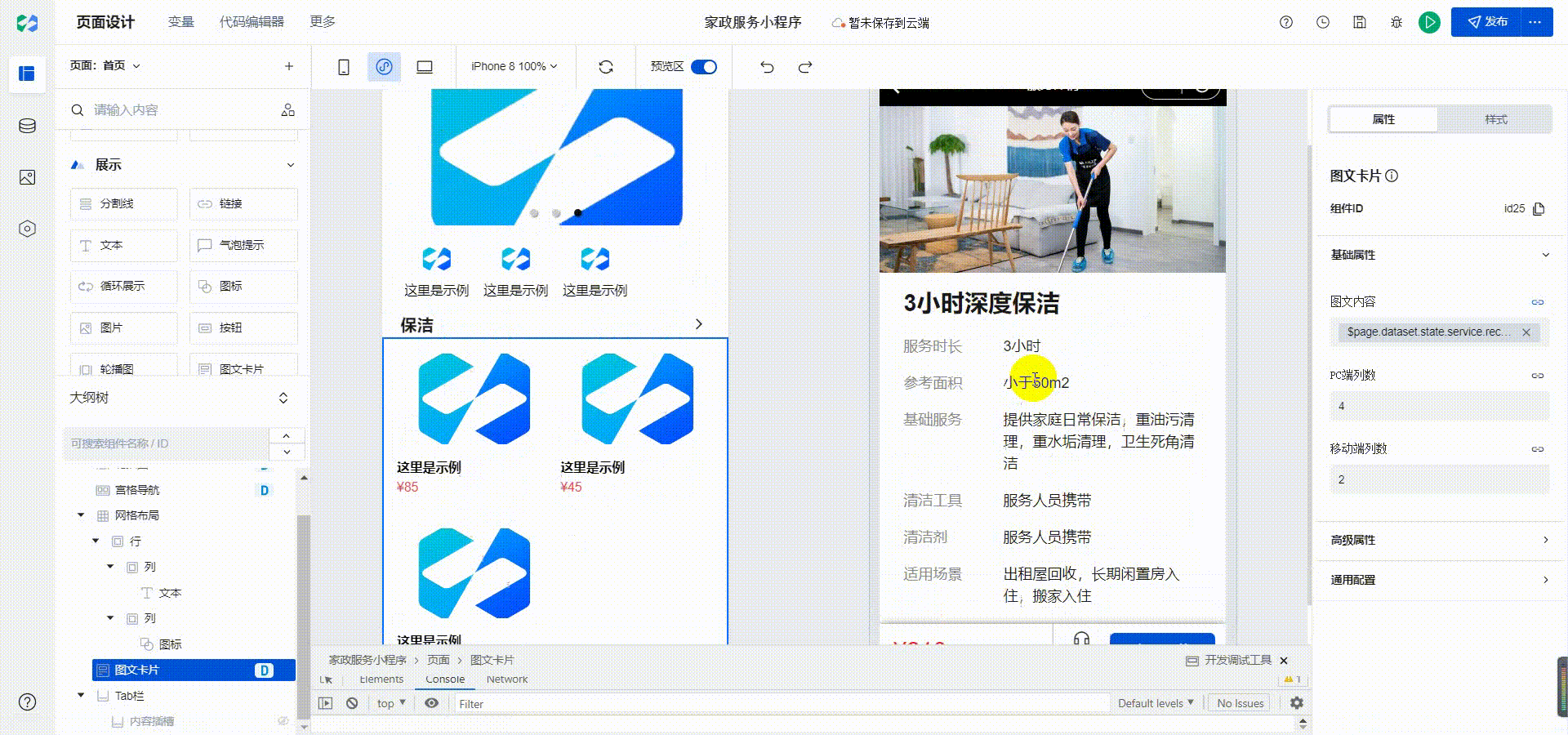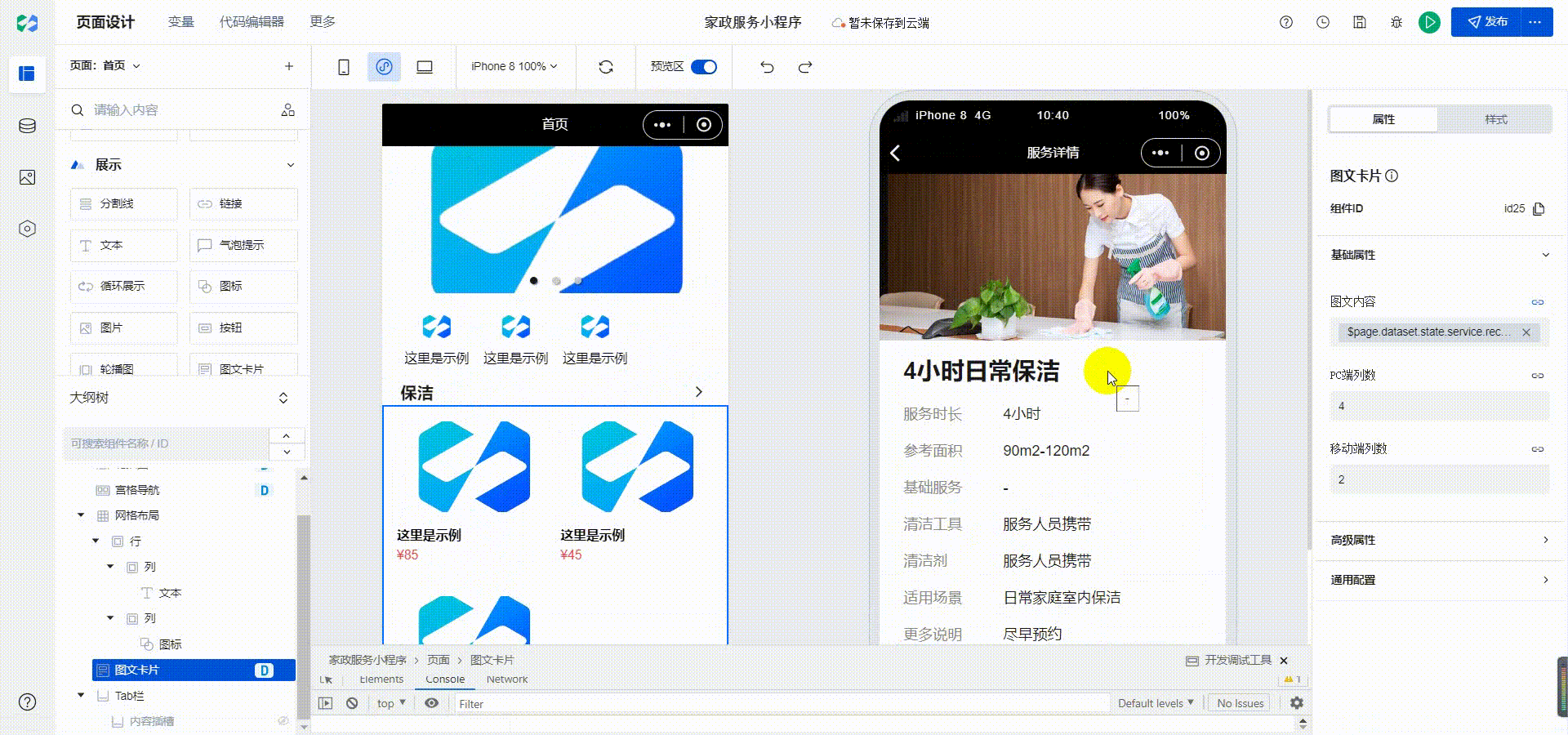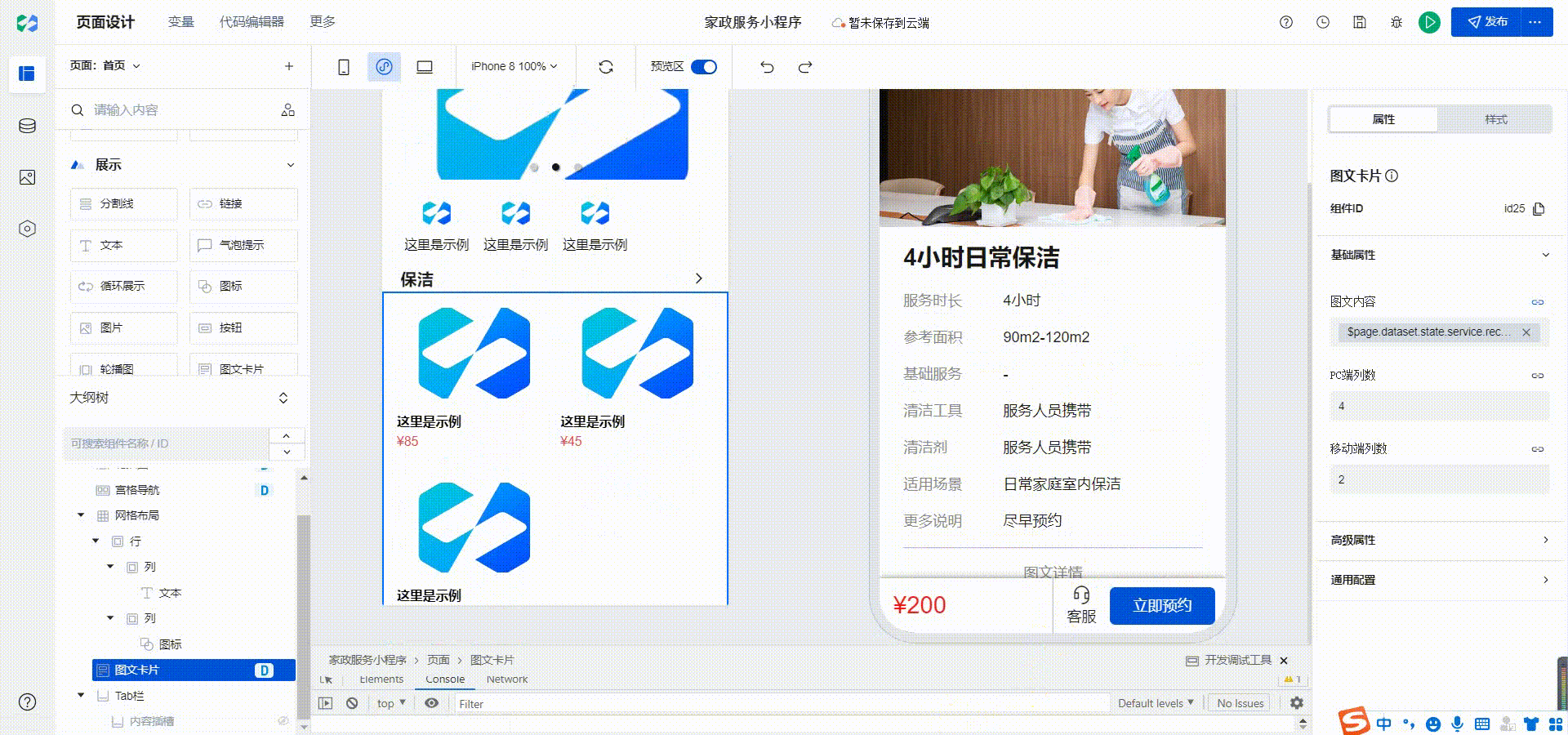
家政服务小程序实战教程12-详情页
我们的家政服务小程序已经完成了首页和分类展示页面的开发,接下来就需要开发详情页了。在详情页里我们展示我们的各项服务内容,让用户可以了解每项家政服务可以提供的内容。 低码开发不像传统开发,如果开发详情页需要考虑每个字段的类型&…...
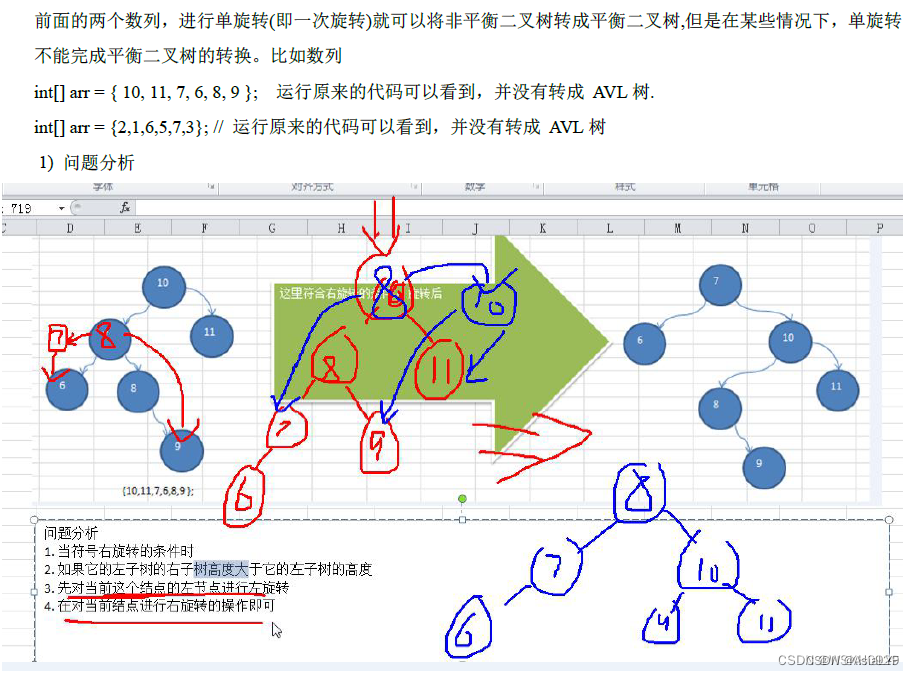
十四、平衡二叉树
1、看一个案例(说明二叉排序树可能的问题) 给你一个数列{1,2,3,4,5,6},要求创建一棵二叉排序树(BST),并分析问题所在。 上面二叉排序树存在问题分析: 左子树全部为空,从形式上看&…...
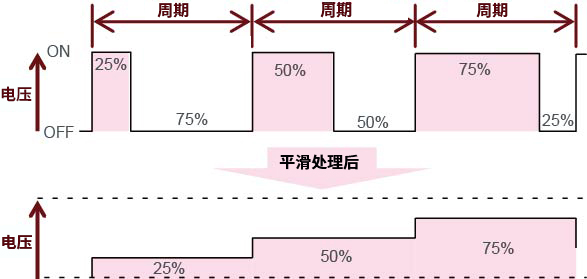
AC/DC 基础
一、概念: AC转换成DC的基本方法有变压器方式和开关方式,如下图1、2所示;整流的基本方法有全波整流和半波整流,如下图3所示。 图1 变压器方式 图2 开关方式 图3 整流方式 二、转换方式 1、变压器方式 变压器方式首先需要通过变压…...

集成电路相关书籍
注:从此开始,文中提到的书籍都会在公众号对应文章末尾给出链接,不需要在微信后台获取,当然还是可以通过在微信后台回复相关书名获取对应的电子书。 在后台看到很多人回复集成电路相关的一些书籍,所以本文就提供一些书籍…...

前端开发之防抖与节流
前端开发中我们经常会通过监听某些事件来完成项目需求 1.通过监听 scroll 事件,检测滚动位置,根据滚动位置显示返回顶部按钮 2.通过监听 resize 事件,对某些自适应页面调整DOM的渲染(通过CSS实现的自适应不再此范围内)…...
大公司如何用A/B测试解决增长问题?
摘要:上线六年,字节跳动的短视频产品——抖音已成为许多人记录美好生活的平台。除了抖音,字节跳动旗下还同时运营着数十款产品,从资讯、游戏,到房产、教育等横跨多个领域。在产品迭代速度和创新能力的快速发展下&#…...
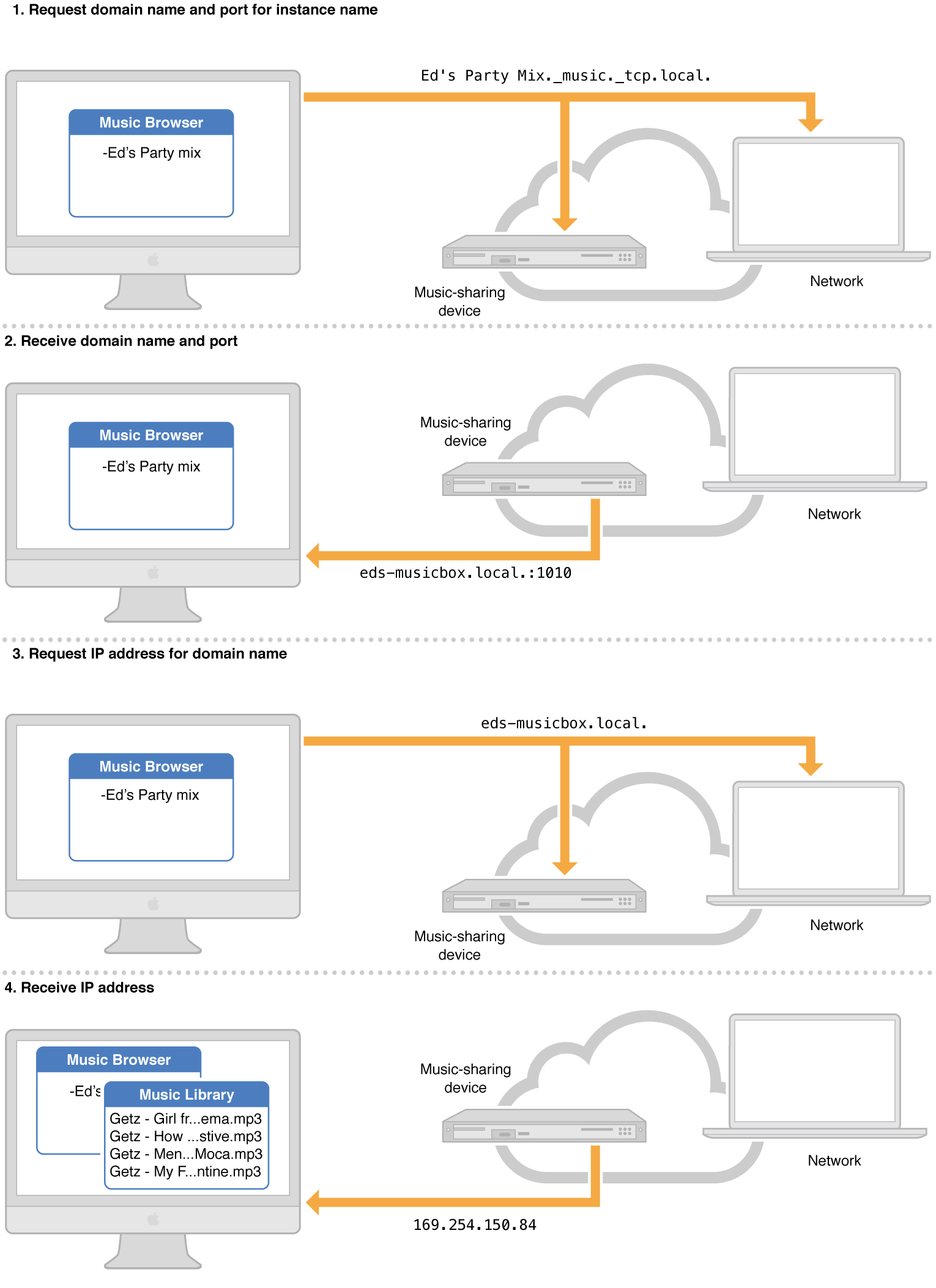
【Airplay_BCT】Bonjour API架构
Bonjour API 架构 OS X 和 iOS 为 Bonjour 服务应用程序提供了多层应用程序编程接口 (API): Foundation 框架中的 NSNetService 和 NSNetServiceBrowser 类; CFNetServices,Core Services 中 CFNetwork 框架的一部分; Java 的 DN…...
为什么sleeping的会话会造成阻塞(2)
背景客户反馈系统突然从11:10开始运行非常缓慢,在SQL专家云中看到大量的产生阻塞的活动会话,KILL掉阻塞的源头马上又出现新的源头,实在没有办法只能重启应用程序断开所有数据库连接才解决,请我们协助分析根本的原因。现象登录SQL专…...

从矩阵中提取对角线元素;将一维数组转换为对角线矩阵:np.diag()函数
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】从矩阵中提取对角线元素将一维数组转换为对角线矩阵np.diag()函数选择题下列说法错误的是?import numpy as npmyarray1 np.array([1,2,3])print("【显示】myarray1")print(myarray1…...
JavaSE学习day7_02 封装和构造方法
4. 封装 面向对象的三大特征: 封装、继承、多态 封装:对象代表什么,就得封装对应的数据,并提供数据对应的行为。 比如人画圆:”画“这个行为应该封装在圆这个类,为什么?因为”画“圆要知道圆…...

2022年FIT2CLOUD飞致云开源成绩单
2023年2月15日,中国领先的开源软件公司FIT2CLOUD飞致云发布《2022年开源成绩单》,盘点公司2022年全年在开源软件产品与社区运营方面的表现。目前,飞致云旗下的核心开源软件组合包括JumpServer开源堡垒机、DataEase开源数据可视化分析平台、Me…...

【Python】asyncio使用注意事项
目录协程的定义协程的运行多个协程运行关于loop.close()回调事件循环协程的定义 需要使用 async def 语句 协程可以做哪些事: 1、等待一个future结果 2、等待另一个协程(产生一个结果或引发一个异常) 3、产生一个结果给正在等它的协程 4、引发一个异常给正在等它的协程 …...

成都链安受邀参加第五届CCF中国区块链技术大会
2月10-12日,由中国计算机学会主办的,2023年国内首场大型区块链学术会议—第五届CCF中国区块链技术大会在无锡市成功举办,成都链安作为区块链安全头部企业受邀参加此次大会。大会上,成都链安创始人&CTO郭文生教授与锡东新城商务…...

验证码识别--封装版
前面我们说过了数字英文的验证码识别操作,本章我们对其进行完善一下,结合selenium来实际操作操作。import osimport timedef coding_path(path):Base_Path os.path.abspath(os.path.dirname(os.path.abspath(__file__)) /..)Base_image os.path.join(…...

创建Wails项目
项目生成 现在 CLI 已安装,您可以使用 wails init 命令生成一个新项目。 选择您最喜欢的框架: SvelteReactVuePreactLitVanilla 使用 JavaScript 生成一个 Vue 项目: wails init -n myproject -t vue如果您更愿意使用 TypeScript: wails init -…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
