【蓝桥集训】第二天——差分
作者:指针不指南吗
专栏:Acwing 蓝桥集训每日一题🐾做题过程中首先应该注意时间复杂度问题🐾
文章目录
- 1.改变数组元素
- 2.差分
- 3.差分矩阵
1.改变数组元素
给定一个空数组 V 和一个整数数组 a1,a2,…,an。
现在要对数组 V 进行 n 次操作。
第 i 次操作的具体流程如下:
- 从数组 V 尾部插入整数 0。
- 将位于数组 V 末尾的 ai 个元素都变为 1(已经是 1 的不予理会)。
注意:
- ai 可能为 0,即不做任何改变。
- ai 可能大于目前数组 V 所包含的元素个数,此时视为将数组内所有元素变为 1。
请你输出所有操作完成后的数组 V。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含整数 n。
第二行包含 n 个整数 a1,a2,…,an。
输出格式
每组数据输出一行结果,表示所有操作完成后的数组 V,数组内元素之间用空格隔开。
数据范围
1≤T≤20000,
1≤n≤2×10510^5105 ,
0≤ai≤n,
保证一个测试点内所有 n 的和不超过 2×10510^5105 。输入样例:
3 6 0 3 0 0 1 3 10 0 0 0 1 0 5 0 0 0 2 3 0 0 0输出样例:
1 1 0 1 1 1 0 1 1 1 1 1 0 0 1 1 0 0 0
- 思路
- 对V进行 n 次操作,每次操作加个 0 ,即V一共有 n 个元素
第 i 次 把 V 末尾的 ai 个元素都变为 1,即 V 是由 0,1 组成
只要被操作过就是 1 ;
- 首先根据数据范围来分析时间复杂度,200010,应该是 n log2nlog_2^nlog2n 或者 n 比较合适
- 用个一个数组来存某个元素操作的次数,超过 1 的输出 1,0就输出 0
- 对 区间 [ n - ai , n ] 统一加上 1,这里可以用差分
- 注意:每一组数据之后,要进行置零

- 代码实现
#include<bits/stdc++.h>
using namespace std;const int N=2*1e5+10;
int a[N];int main()
{int T;cin>>T; // T 组测试数据while(T--){int n; // n 个元素cin>>n;memset(a,0,(n+1)*4); //置零操作,memset 或者是 for(快些),sizeof b 会比(n+1)*4 慢很多 for(int i=1;i<=n;i++){ //输入数据int x;cin>>x; int l=max(1,i-x+1),r=i; a[l]++,a[r+1]--; //记录V中元素被操作多少次 差分} for(int i=1;i<=n;i++){a[i]+=a[i-1]; // 为什么求前缀和数组,算的差分数组不是记录的 V 中元素操作的次数吗?cout<<!!a[i]<<' '; // !! 运算,如果是0,则为0,如果是非0,则为1,也可以写特判}cout<<endl;}return 0;
}
2.差分
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c表示将序列中 [l, r ]之间的每个数加上 。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000,输入样例:
6 3 1 2 2 1 2 1 1 3 1 3 5 1 1 6 1输出样例:
3 4 5 3 4 2
- 代码实现
#include<iostream>
using namespace std;const int N=100010;
int a[N],b[N];int n,m; //n 数组元素个数;m 表示操作次数void insert(int l,int r,int c){b[l]+=c; //对差分+cb[r+1]-=c; //补丁
}int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];insert(i,i,a[i]); //差分b 数组}while(m--){int l,r,c; //对差分 b 操作cin>>l>>r>>c; insert(l,r,c); //对区间进行元素进行操作}for(int i=1;i<=n;i++){ //求出原数组即前缀和aa[i]=a[i-1]+b[i];cout<<a[i]<<' ';}return 0;
}
3.差分矩阵
输入一个 n 行 m 列的整数矩阵,再输入 q个操作,每个操作包含五个整数 x1,y1,x2,y2,c,
其中 (x1,y1)和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 55 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000.输入样例:
3 4 3 1 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 1 1 3 2 3 2 3 1 3 4 1输出样例:
2 3 4 1 4 3 4 1 2 2 2 2
-
代码实现
#include <iostream>using namespace std;const int N = 1010;int n, m, q; int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c) {b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c; }int main() {scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ ){scanf("%d", &a[i][j]);insert(i, j, i, j, a[i][j]);}while (q -- ){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i ++ ){for (int j = 1; j <= m; j ++ ){b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];printf("%d ", b[i][j]);}puts(" ");}return 0; }

相关文章:

【蓝桥集训】第二天——差分
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾做题过程中首先应该注意时间复杂度问题🐾 文章目录1.改变数组元素2.差分3.差分矩阵1.改变数组元素 给定一个空数组 V 和一个整数数组 a1,a2,…,an。 现在要对数组 V 进行 n 次操…...

Spring Boot最核心的27个注解,你了解多少?
https://blog.csdn.net/ManuMAX/article/details/129017443 导读 Spring Boot方式的项目开发已经逐步成为Java应用开发领域的主流框架,它不仅可以方便地创建生产级的Spring应用程序,还能轻松地通过一些注解配置与目前比较火热的微服务框架SpringCloud集成…...

css3弹性盒子
弹性盒子由弹性容器(Flex container)和弹性子元素(Flex item)组成。 弹性容器通过设置 display 属性的值为 flex 或 inline-flex将其定义为弹性容器。 弹性容器内包含了一个或多个弹性子元素。 display:flex; 修改排列方式: 0. direction: rtl; //(right-to-left),弹性子元素的…...
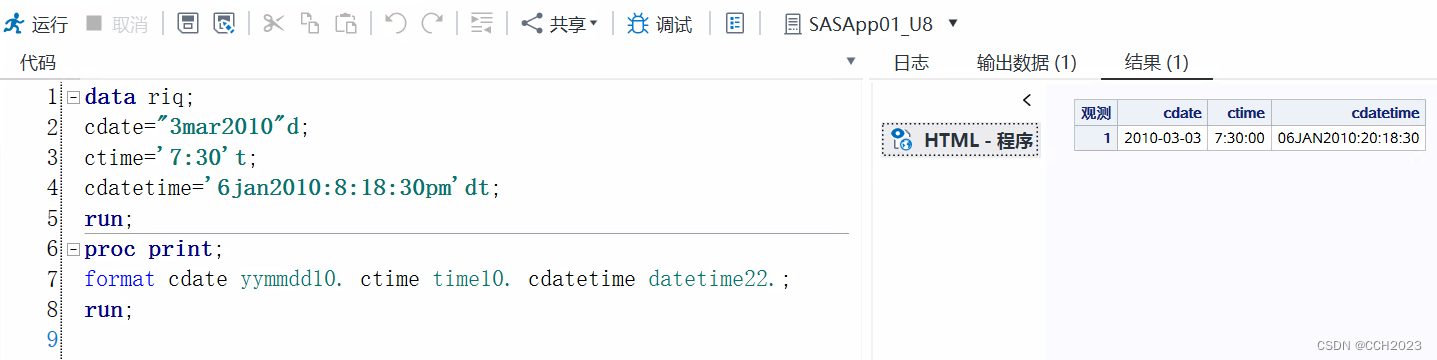
数据分析与SAS学习笔记2
SAS在企业使用的情况: SAS是一个很昂贵的商业软件。在企业中使用SAS比较多,在企业界中是比较流行,在学术界使用R比较多。 SAS简介:统计分析系统 处理生物分析数据。 SAS成为统计领域的国际标准软件,服务全球50000多家…...
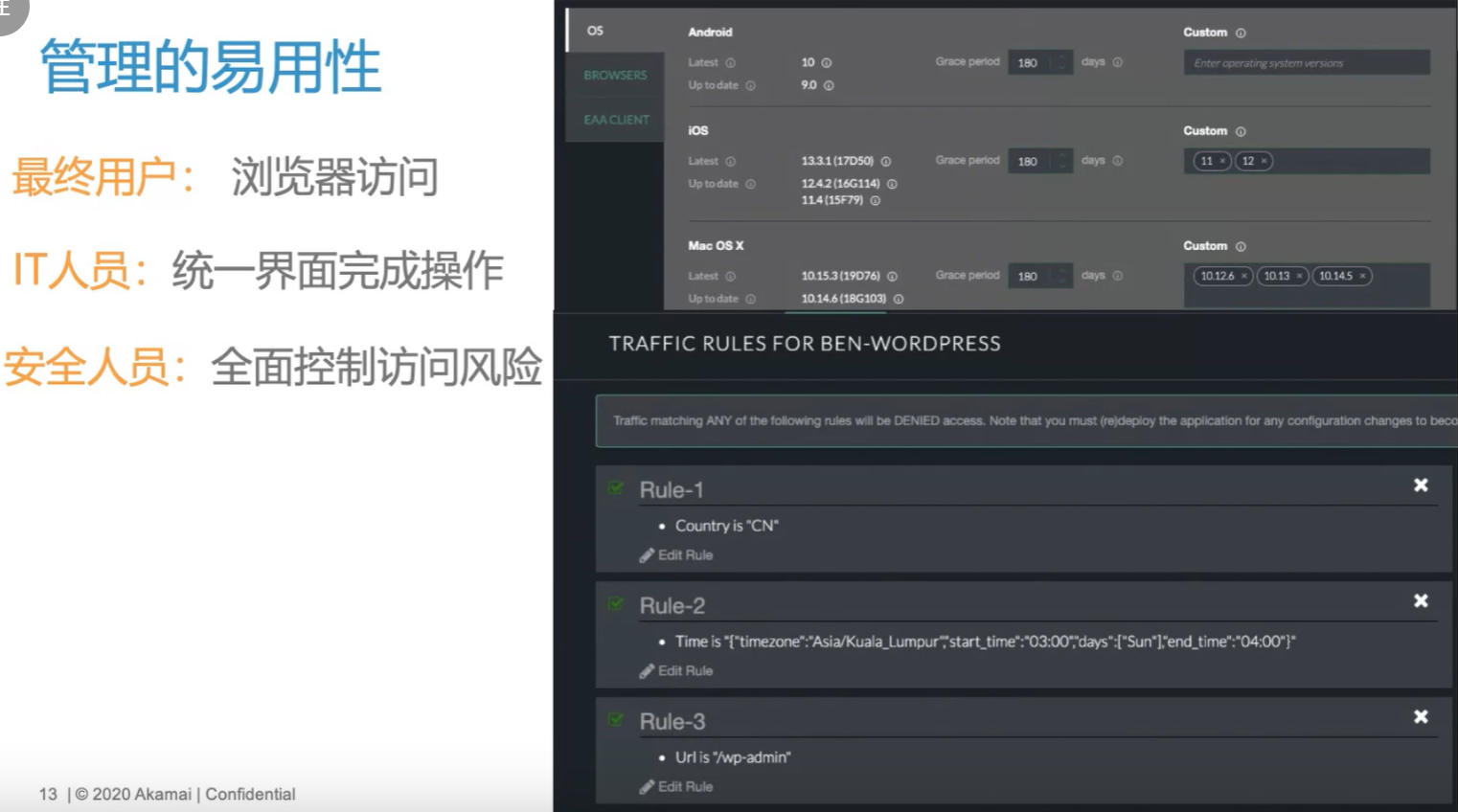
零信任-Akamai零信任介绍(6)
Akamai零信任介绍 Akamai是一家专注于分布式网络服务的公司,它提供了一系列的互联网内容和应用加速服务。关于Akamai的零信任,它指的是Akamai的安全架构中不存在任何一个环节是可以被单独的控制或影响的,因此可以提供更高的安全性。通过使…...
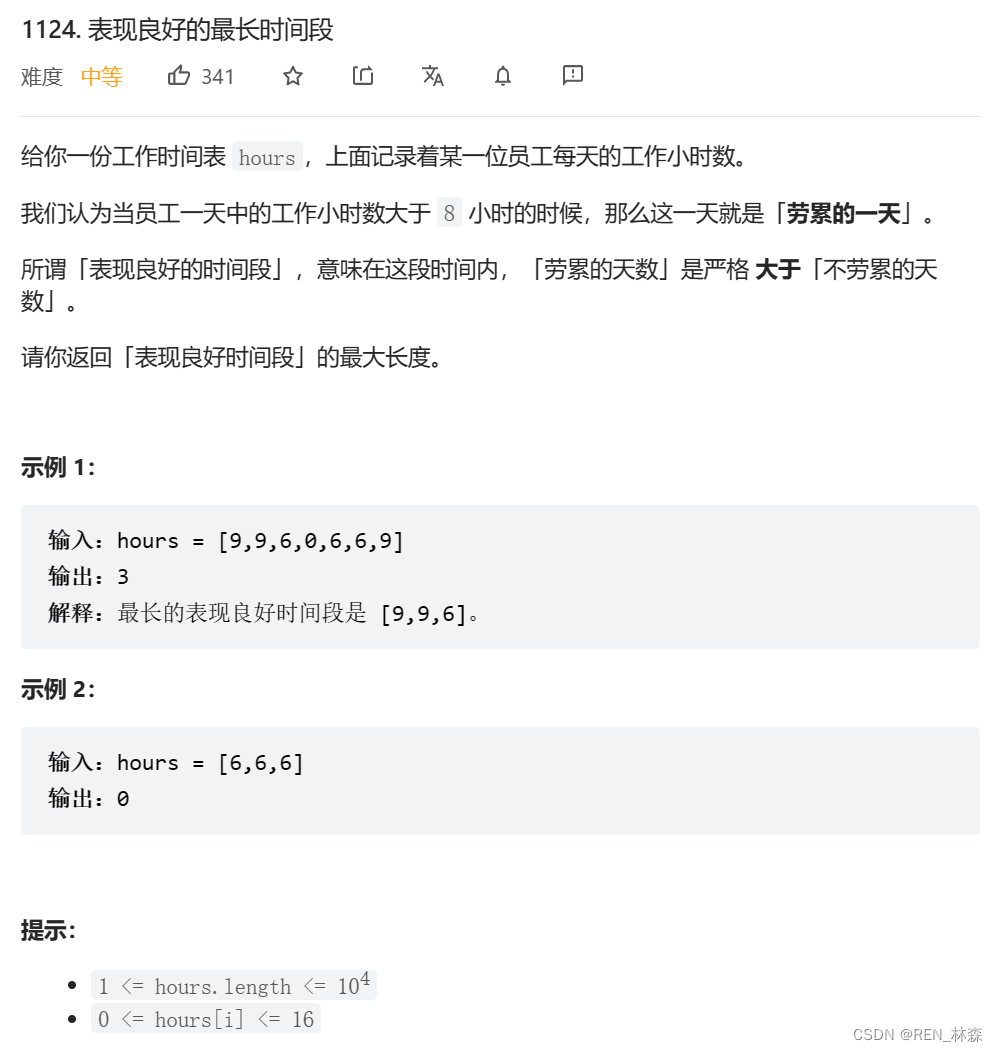
表现良好的最长时段[前缀和思想子数组]
前缀和与最长子数组前言一、表现良好的最长时间段二、前缀和思想&子数组1、前缀和&map2、前缀和&单调栈总结参考文献前言 对于子数组/子串问题,紧密连续前缀和/滑动窗口/单调栈;挖掘内在规律,可以简化代码,降低时空复…...

Python 获取当前系统时间
在有的时候,系统不能联网,需要获取系统的当前实现,此时需要python的datetime库。 一、使用方法 1. 导入库:import datetime 2.获取当前日期和时间:now_time datetime.datetime.now() 3.格式化成我们想要的格式&am…...
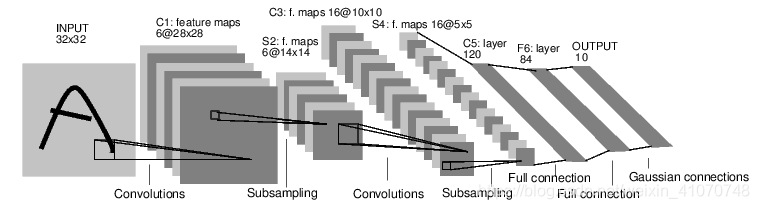
pytorch基础入门教程
pytorch基础入门教程 Pytorch一小时入门教程 前言 机器学习的门槛并没有想象中那么高,我会陆续把我在学习过程中看过的一些文章和写过的代码以博客的形式分享给大家,和大家一起交流,这个是本系列的第一篇,pytoch入门教程&#x…...
RTSP协议交互时TCP/UDP的区别 以及视频和音频的区别 以及H264/H265的区别
经过这几天的调试 一个功能简单的 RTSP服务端已经实现了 支持TCP/UDP 支持H264 H265 支持同时传输 AAC音频 记录下 交互时需要注意的地方 1.OPTIONS 都一样 如下:左箭头内是客户端发给服务端 箭头内是服务端回给客户端 2.DESCRIBE 目前的流是包含视频和AAC音频…...

调用大智慧L2接口是什么原理?作用是什么?
有些开发人员想要设计一个微信公众号或者微信小程序,由于自己搭建数据库工作量太大,或者技术受限,也会选择调用大智慧L2接口减少工作量。调用大智慧L2接口是什么原理?作用是什么? 大智慧L2接口即应用程序编程接口&…...
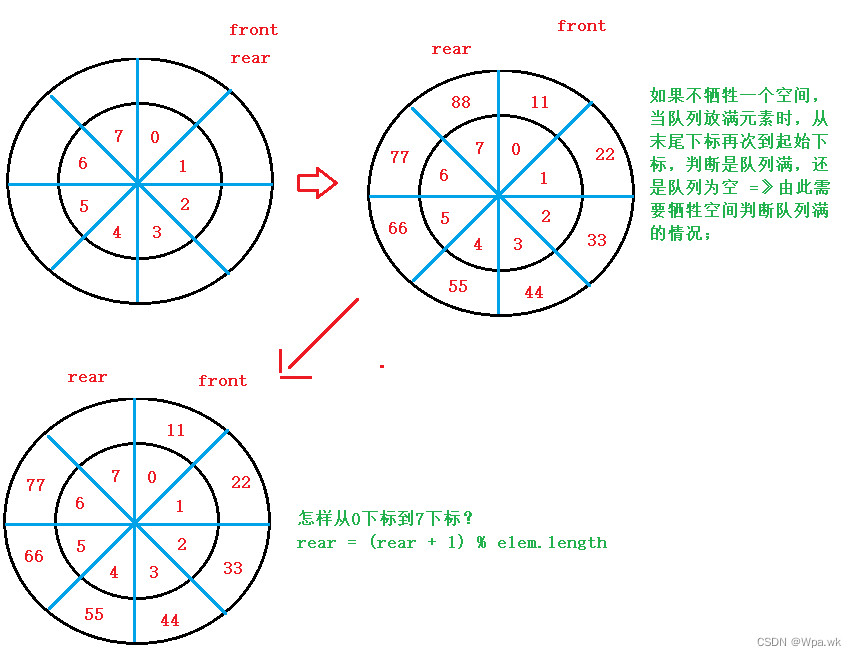
数据结构 - 栈 与 队列 - (java)
前言 本篇介绍栈和队列,了解栈有顺序栈和链式栈,队列底层是双链表实现的,单链表也可以实现队列,栈和队列的相互实现和循环队列;如有错误,请在评论区指正,让我们一起交流,共同进步&a…...

CellularAutomata元胞向量机-8-渗流集群MATLAB代码分享
%% Percolation Clusterclf clc, clearthreshold .63; % ax axes(units,pixels,position,[1 1 650 700],color,k); text(units, pixels, position, [150,255,0],... string,美赛,color,w,fontname,helvetica,fontsize,100) text(units, pixels, position, [40,120,0],... str…...

iOS UI自动化测试详解
前言: 小目标 关于UI自动化的定义,我想要的是自动地按照流程去点击页面、输入数据,不需要人去参与,节省人工时间。比如登录,能够自己去填写用户名&密码,然后点击按钮跳转到下一个页面等。在能够保证业…...
Mybatis源码分析(九)Mybatis的PreparedStatement
文章目录一 JDBC的PreparedStatement二 prepareStatement的准备阶段2.1 获取Connection2.1.1 **UnpooledDataSource**2.1.2 PooledDataSource2.2 Sql的预编译PreparedStatementHandler2.3 为Statement设置参数2.4 执行具体的语句过程官网:mybatis – MyBatis 3 | 简…...

winfrom ui
http://www.iqidi.com/download/warehouse/Device_DotNetBar.rar http://qiosdevsuite.com/Download https://sourceforge.net/projects/qiosdevsuite/ https://www.cnblogs.com/hcyblogs/p/6758381.html https://www.cnblogs.com/jordonin/p/6484366.html MBTiles地图瓦片管…...
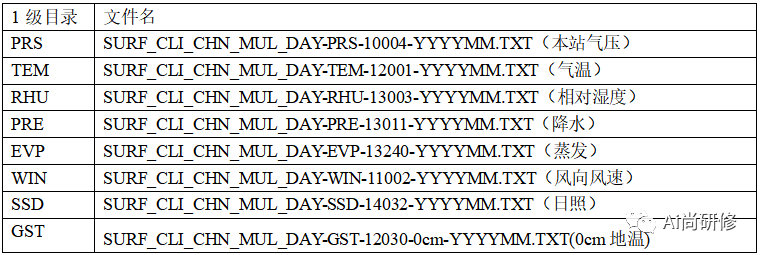
中国国家级地面气象站基本气象要素日值数据集(V3.0)
数据集摘要 数据集包含了中国基本气象站、基准气候站、一般气象站在内的主要2474个站点1951年1月以来本站气压、气温、降水量、蒸发量、相对湿度、风向风速、日照时数和0cm地温要素的日值数据。数据量为21.3GB。 (1)SURF_CLI_CHN_MUL_DAY-TEM-12001-201501.TXT 气温数据TEM, 包…...

【Python语言基础】——Python NumPy 数组副本 vs 视图
Python语言基础——Python NumPy 数组副本 vs 视图 文章目录 Python语言基础——Python NumPy 数组副本 vs 视图一、Python NumPy 数组副本 vs 视图一、Python NumPy 数组副本 vs 视图 副本和视图之间的区别 副本和数组视图之间的主要区别在于副本是一个新数组,而这个视图只是…...
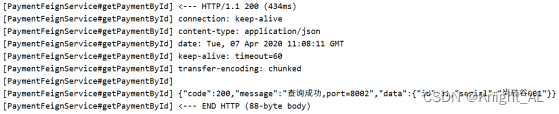
Spring Cloud_OpenFeign服务接口调用
目录一、概述1.OpenFeign是什么2.能干嘛二、OpenFeign使用步骤1.接口注解2.新建Module3.POM4.YML5.主启动类6.业务类7.测试8.小总结三、OpenFeign超时控制1.超时设置,故意设置超时演示出错情况2.是什么3.YML中需要开启OpenFeign客户端超时控制四、OpenFeign日志打印…...

十三、GIO GTask
GTask表示管理一个可取消的“任务task” GCancellable GCancellable是一个线程安全的操作取消栈,用于整个GIO,以允许取消同步和异步操作。 它继承于GObject对象,不是一个单纯的结构体 相关函数 g_task_new GTask* g_task_new (GObject*…...
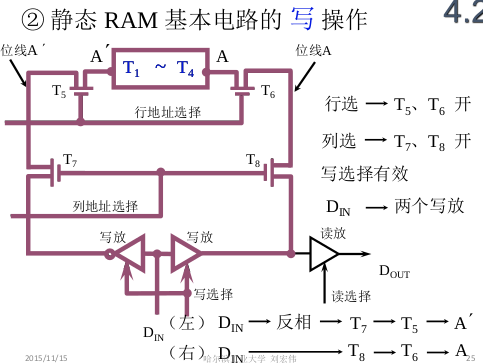
ch4_1存储器
1. 存储器的类型 1.1 按照存储介质来分类 半导体存储器: TTL, MOS 易失性 磁表面存储器: 磁头, 载磁体; 磁芯存储器: 硬磁材料, 环状元件 光盘存储器: 激光, 磁光材料; 1.2 按…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
