LeetCode 2341. 数组能形成多少数对
【LetMeFly】2341.数组能形成多少数对
力扣题目链接:https://leetcode.cn/problems/maximum-number-of-pairs-in-array/
给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤:
- 从
nums选出 两个 相等的 整数 - 从
nums中移除这两个整数,形成一个 数对
请你在 nums 上多次执行此操作直到无法继续执行。
返回一个下标从 0 开始、长度为 2 的整数数组 answer 作为答案,其中 answer[0] 是形成的数对数目,answer[1] 是对 nums 尽可能执行上述操作后剩下的整数数目。
示例 1:
输入:nums = [1,3,2,1,3,2,2] 输出:[3,1] 解释: nums[0] 和 nums[3] 形成一个数对,并从 nums 中移除,nums = [3,2,3,2,2] 。 nums[0] 和 nums[2] 形成一个数对,并从 nums 中移除,nums = [2,2,2] 。 nums[0] 和 nums[1] 形成一个数对,并从 nums 中移除,nums = [2] 。 无法形成更多数对。总共形成 3 个数对,nums 中剩下 1 个数字。
示例 2:
输入:nums = [1,1] 输出:[1,0] 解释:nums[0] 和 nums[1] 形成一个数对,并从 nums 中移除,nums = [] 。 无法形成更多数对。总共形成 1 个数对,nums 中剩下 0 个数字。
示例 3:
输入:nums = [0] 输出:[0,1] 解释:无法形成数对,nums 中剩下 1 个数字。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
方法一:哈希表
我们可以使用一个哈希表来统计某个数x是否出现过。(开辟长度为100的数组来统计也可以)
初始时哈希表为空,接着遍历原始数组,如果数组中的某个数在哈希表中,则“配对成功”,成功次数加一并将这个数从哈希表中移除;否则直接将这个数插入哈希表中等待配对即可。
最终返回配对成功次数,原始数组长度−2×配对成功次数{配对成功次数, 原始数组长度 - 2\times 配对成功次数}配对成功次数,原始数组长度−2×配对成功次数即可
- 时间复杂度O(len(nums))O(len(nums))O(len(nums))
- 空间复杂度O(len(nums))O(len(nums))O(len(nums))
AC代码
C++
class Solution {
public:vector<int> numberOfPairs(vector<int>& nums) {unordered_set<int> se;int cntPair = 0;for (int& t : nums) {if (se.count(t)) {se.erase(t);cntPair++;}else {se.insert(t);}}return {cntPair, (int)nums.size() - cntPair * 2};}
};
Python
# from typing import Listclass Solution:def numberOfPairs(self, nums: List[int]) -> List[int]:se = set()cntPair = 0for i in nums:if i in se:se.remove(i)cntPair += 1else:se.add(i)return [cntPair, len(nums) - cntPair * 2]
同步发文于CSDN,原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/129055398
相关文章:

LeetCode 2341. 数组能形成多少数对
【LetMeFly】2341.数组能形成多少数对 力扣题目链接:https://leetcode.cn/problems/maximum-number-of-pairs-in-array/ 给你一个下标从 0 开始的整数数组 nums 。在一步操作中,你可以执行以下步骤: 从 nums 选出 两个 相等的 整数从 nums…...

PHPStorm常用快捷键
alt 1 左侧项目结构树隐藏或者显示,这两个组合键的使用可以切换“项目结构树”和当前打开文件之间的焦点。 alt 2 隐藏或者显示 Favorites Ctrl Shift F12 切换到最大编辑器窗口,隐藏其他所有的工具窗口。例如项目结构树、Favorites、Terminal等。…...
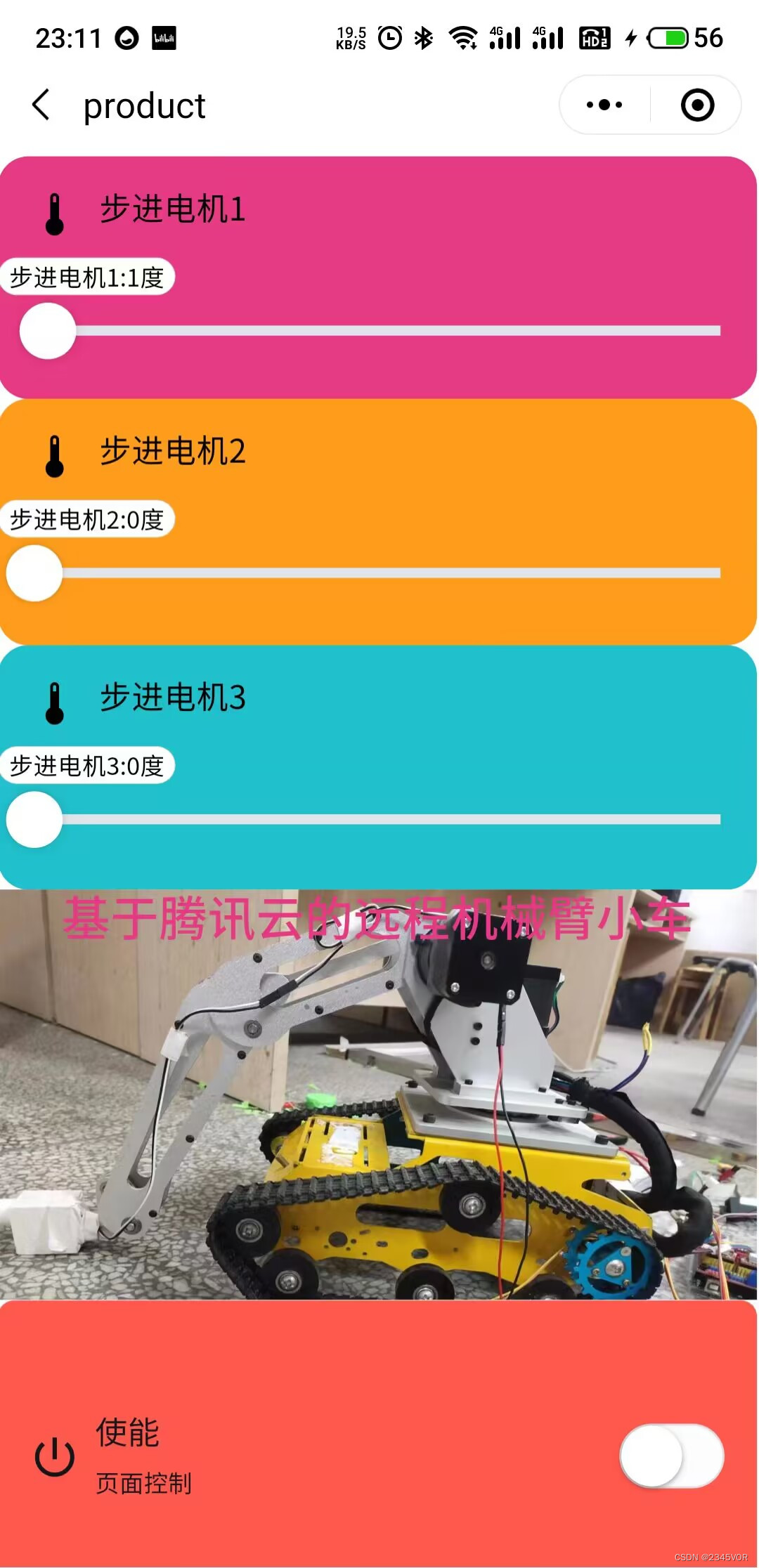
【基于腾讯云的远程机械臂小车】
【基于腾讯云的远程机械臂小车】1. 项目来源1.1 项目概述1.2 系统结构1.3 设计原理2. 硬件搭建2.1 CH32V307开发板2.2 Arduino mega25602.3 富斯I6遥控器2.4 机械臂小车2.5 ESP8266 MCU2.5.1 ESP8266 MCU介绍2.5.2 腾讯云固件烧录3. 软件设计3.1 两种控制方式3.1.1 富斯I6遥控机…...

兼职任务平台收集(一)分享给有需要的朋友们
互联网时代,给人们带来了很大的便利。信息交流、生活缴费、足不出户购物、便捷出行、线上医疗、线上教育等等很多。可以说,网络的时代会一直存在着。很多人也在互联网上赚到了第一桶金,这跟他们的努力和付出是息息相关的。所谓一份耕耘&#…...

MarkDown中公式的编辑
MarkDown中公式的编辑生成目录积分插入编号常见希腊字母大小写分式括号求和积分连乘根式三角函数运算符集合运算箭头逻辑运算符约等于向量绝对值申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计1077字&…...
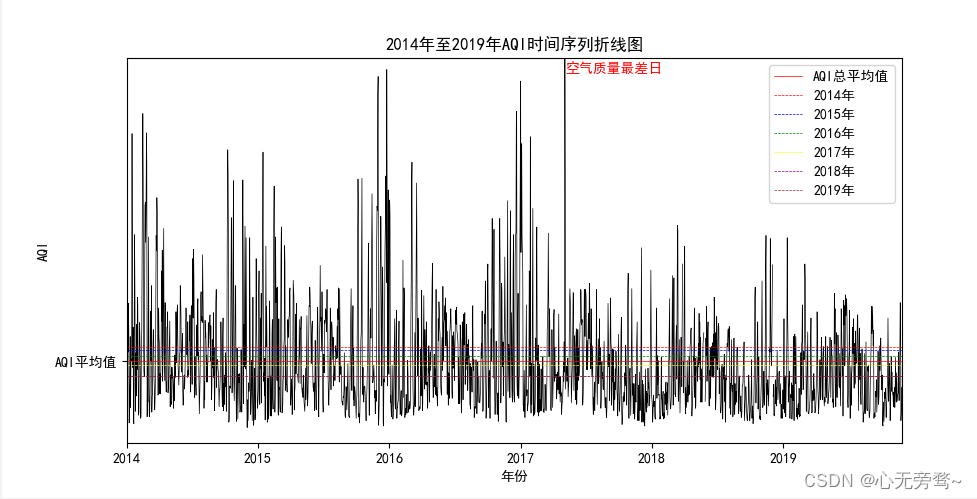
解决jupyter以及windows系统中pycharm编译器画图的中文乱码问题大全
一、jupyter环境下中文乱码问题解决 我们在jupyter的notebook中使用matplotlib画图的时候,经常性的会遇见一些中文乱码显示□的情况,如下所示: 在此,网上给出的方法大多是以下的解决方法: import matplotlib.pyplot as pltplt.rcParams[fo…...
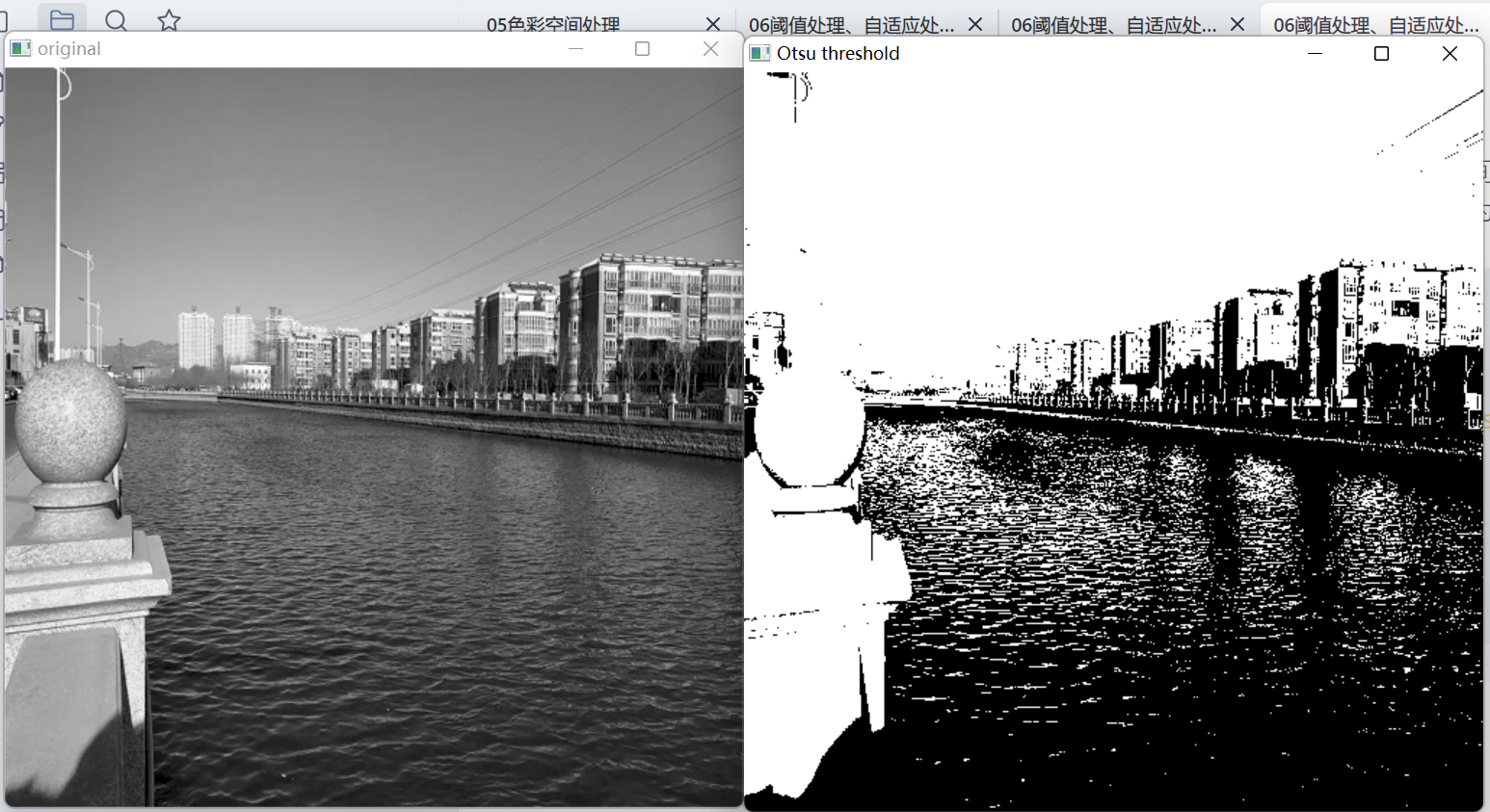
06 OpenCV 阈值处理、自适应处理与ostu方法
1 基本概念 CV2中使用阈值的作用是将灰度图像二值化,即将灰度图像的像素值根据一个设定的阈值分成黑白两部分。阈值处理可以用于图像分割、去除噪声、增强图像对比度等多个领域。例如,在物体检测和跟踪中,可以通过对图像进行阈值处理来提取目…...

RFC7519规范-JWT - json web token
简介 什么是JWT(JSON Web Token) 在介绍JWT之前,我们先来回顾一下利用token进行用户身份验证的流程: 客户端使用用户名和密码请求登录服务端收到请求,验证用户名和密码验证成功后,服务端会签发一个token,再把这个to…...

移动机器人设计与实践课程大纲
MiR移动机器人参考资料:图一 西北工业大学-课程平台图二 清华大学出版社-移动机器人目前,基本都是双一流大学开设此类课程,并且都是至少3-4学分,16学时/学分,48-64学时。(⊙﹏⊙),难办了。咱这只有…...
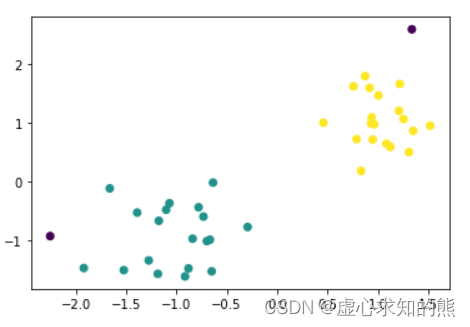
Lesson 7.2 Mini Batch K-Means与DBSCAN密度聚类
文章目录一、Mini Batch K-Means 算法原理与实现二、DBSCAN 密度聚类基本原理与实践1. K-Means 聚类算法的算法特性2. DBSCAN 密度聚类基本原理3. DBSCAN 密度聚类的 sklearn 实现除了 K-Means 快速聚类意外,还有两种常用的聚类算法。(1) 是能…...

11.Dockerfile最佳实践
Dockerfile 最佳实践 Docker官方关于Dockerfile最佳实践原文链接地址:https://docs.docker.com/develop/develop-images/dockerfile_best-practices/ Docker 可以通过从 Dockerfile 包含所有命令的文本文件中读取指令自动构建镜像,以便构建给定镜像。 …...
【企业云端全栈开发实践-1】项目介绍及环境准备、Spring Boot快速上手
本节目录一、 项目内容介绍二、Maven介绍2.1 Maven作用2.2 Maven依赖2.3 本地仓库配置三、Spring Boot快速上手3.1 Spring Boot特点3.2 遇到的Bug:spring-boot-maven-plugin3.3 遇到的Bug2:找不到Getmapping四、开发环境热部署一、 项目内容介绍 本课程…...
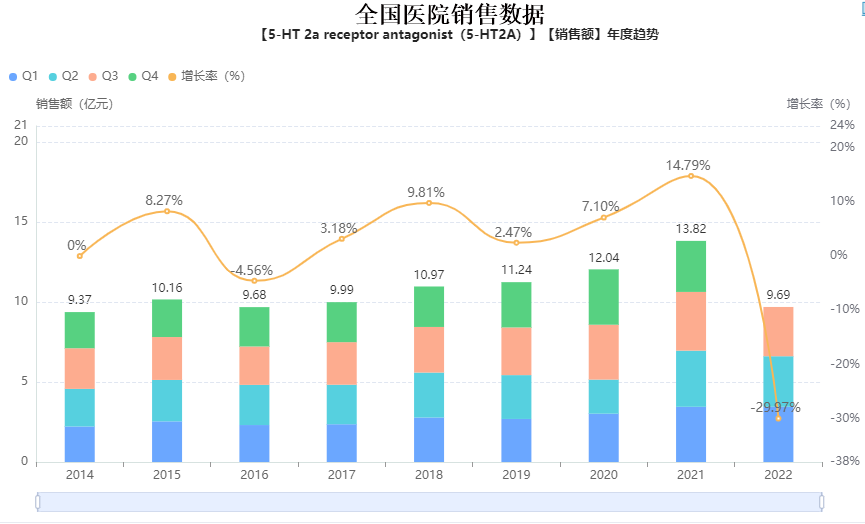
5-HT2A靶向药物|适应症|市场销售-上市药品前景分析
据世界卫生组织称,抑郁症是一种多因素疾病,影响全球约3.5 亿人。中枢神经系统最广泛的单胺 - 血清素 (5-HT) 被认为在这种情况的病理机制中起着至关重要的作用,并且神经递质的重要性被“血清素假说”提升,将抑郁症的存在联系起来 …...

HTTPS协议原理---详解
目录 一、HTTPS 1.加密与解密 2.我们为什么要加密? 3.常见加密方式 ①对称加密 ②非对称加密 4.数据摘要 5.数字签名 二、HTTPS的加密方案 1.只是用对称加密 2.只使用非对称加密 3.双方都使用非对称加密 4.非对称加密+对称加密 中间人攻…...
Pytest学习笔记
Pytest学习笔记 1、介绍 1.1、单元测试 单元测试是指在软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试 1.2、单元测试框架 测试发现:从多个py文件里面去找到我们测试用例测试执行:按…...
Fuzz概述
文章目录AFL一些概念插桩与覆盖率边和块覆盖率afl自实现劫持汇编器clang内置覆盖率反馈与引导变异遗传算法fork server机制AFL调试准备AFL一些概念 插桩与覆盖率 边和块 首先,要明白边和块的定义 正方形的就是块,箭头表示边,边表示程序执行…...
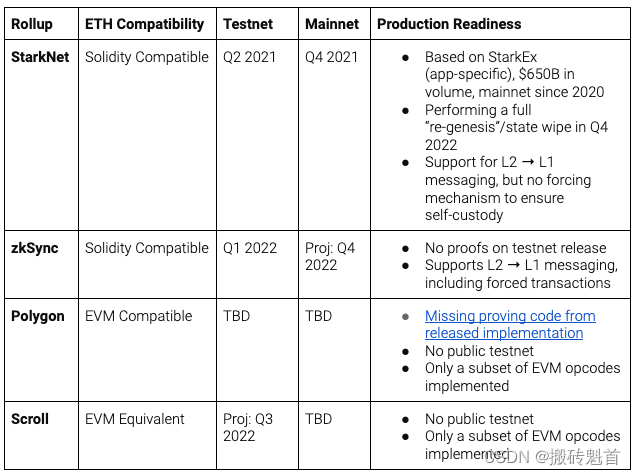
区块链知识系列 - 系统学习EVM(四)-zkEVM
区块链知识系列 - 系统学习EVM(一) 区块链知识系列 - 系统学习EVM(二) 区块链知识系列 - 系统学习EVM(三) 今天我们来聊聊 zkEVM、EVM 兼容性 和 Rollup 是什么? 1. 什么是 Rollup rollup顾名思义,就是把一堆交易卷(rollup)起来…...

Leetcode.2341 数组能形成多少数对
题目链接 Leetcode.2341 数组能形成多少数对 Rating : 1185 题目描述 给你一个下标从 0 开始的整数数组 nums。在一步操作中,你可以执行以下步骤: 从 nums选出 两个 相等的 整数从 nums中移除这两个整数,形成一个 数对 请你在 nums上多次执…...

C++复习笔记10
1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过指针指向其前一个元素和后一个元素。 3. list与for…...
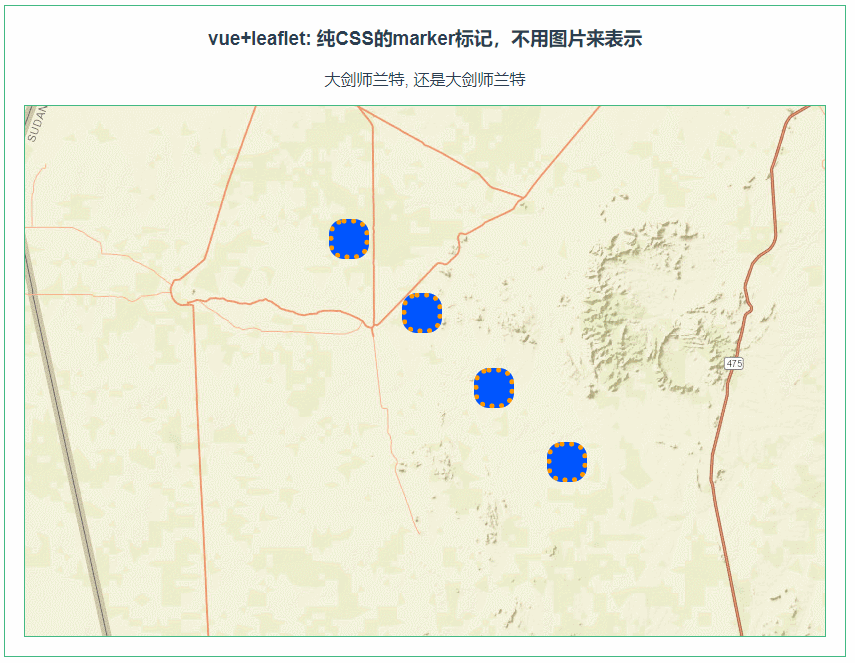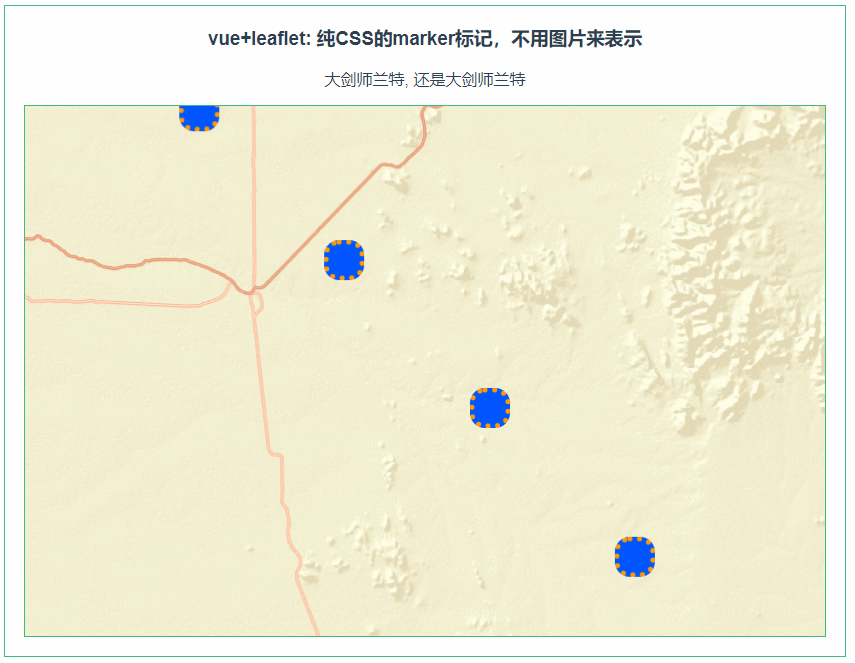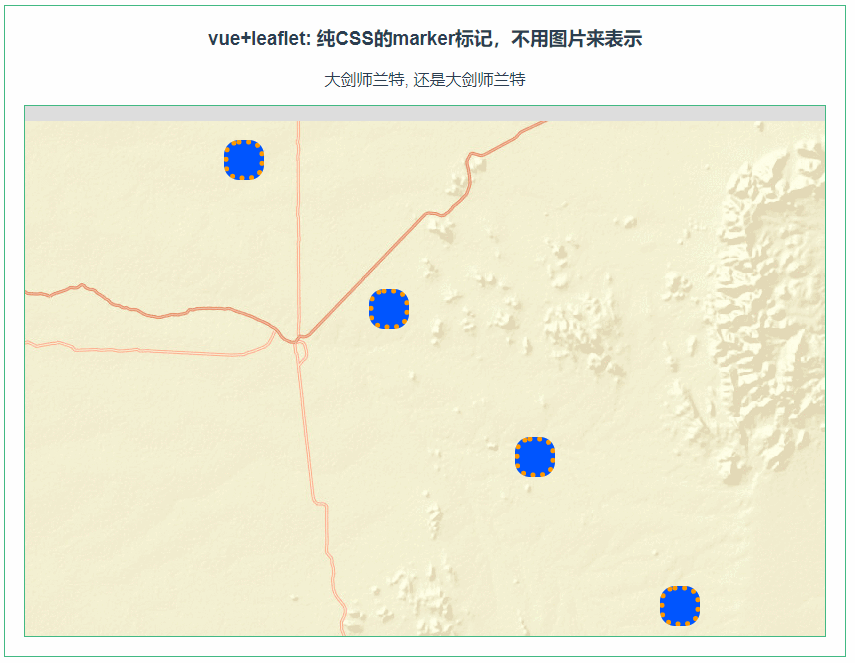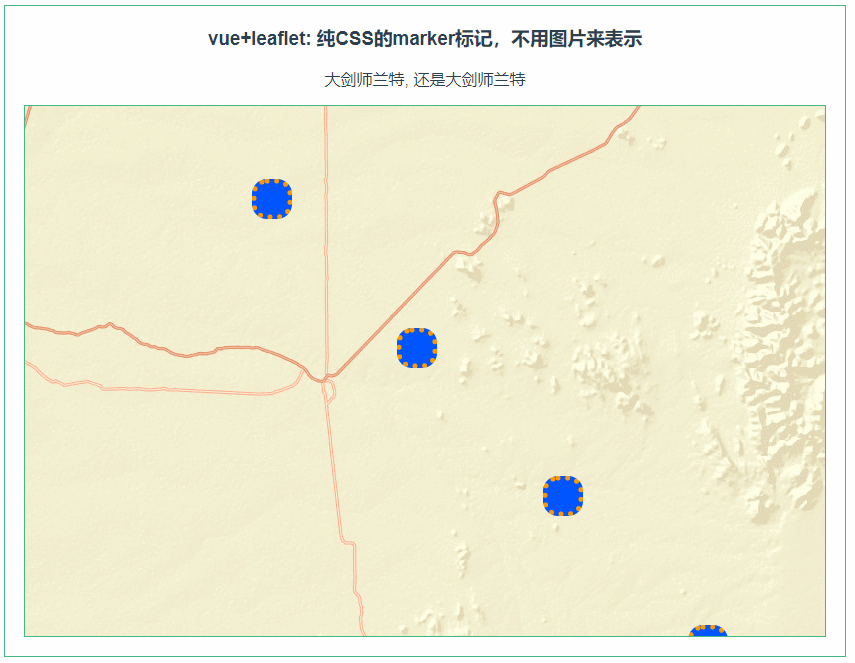
leaflet 纯CSS的marker标记,不用图片来表示(072)
第072个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用纯CSS来打造marker的标记。这里用到的是L.divIcon来引用CSS来构造新icon,然后在marker的属性中引用。 这里必须要注意的是css需要是全局性质的,不能被scoped转义为其他随机的css。 直接复制下面的 v…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
